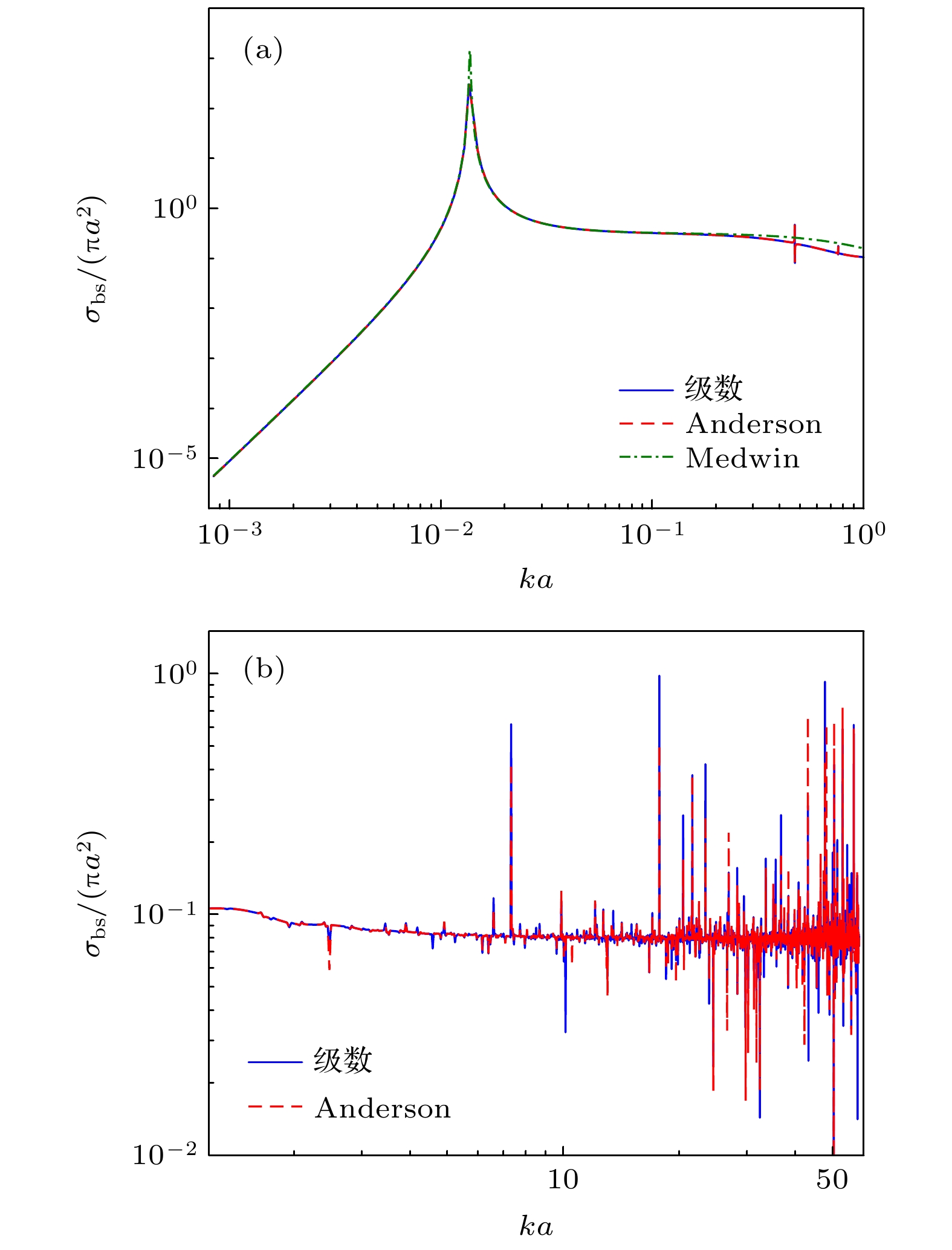
-
Ultrasonic detection is an effective method to quantify bubbles in opaque liquid, and acoustic scattering model is the key in ultrasonic inversion technique. Classical scattering models are usually based on the spherical assumption, and ka is much less than 1. However, these conditions are not always satisfied in practical applications. In this study, a quantitative strategy of ultrasonic inversion is proposed for non-spherical bubbles and ka deviation assumption. A series of solution models for a spherical gas bubble is established without considering the ka constraint, and it is compared with the classical Medwin (
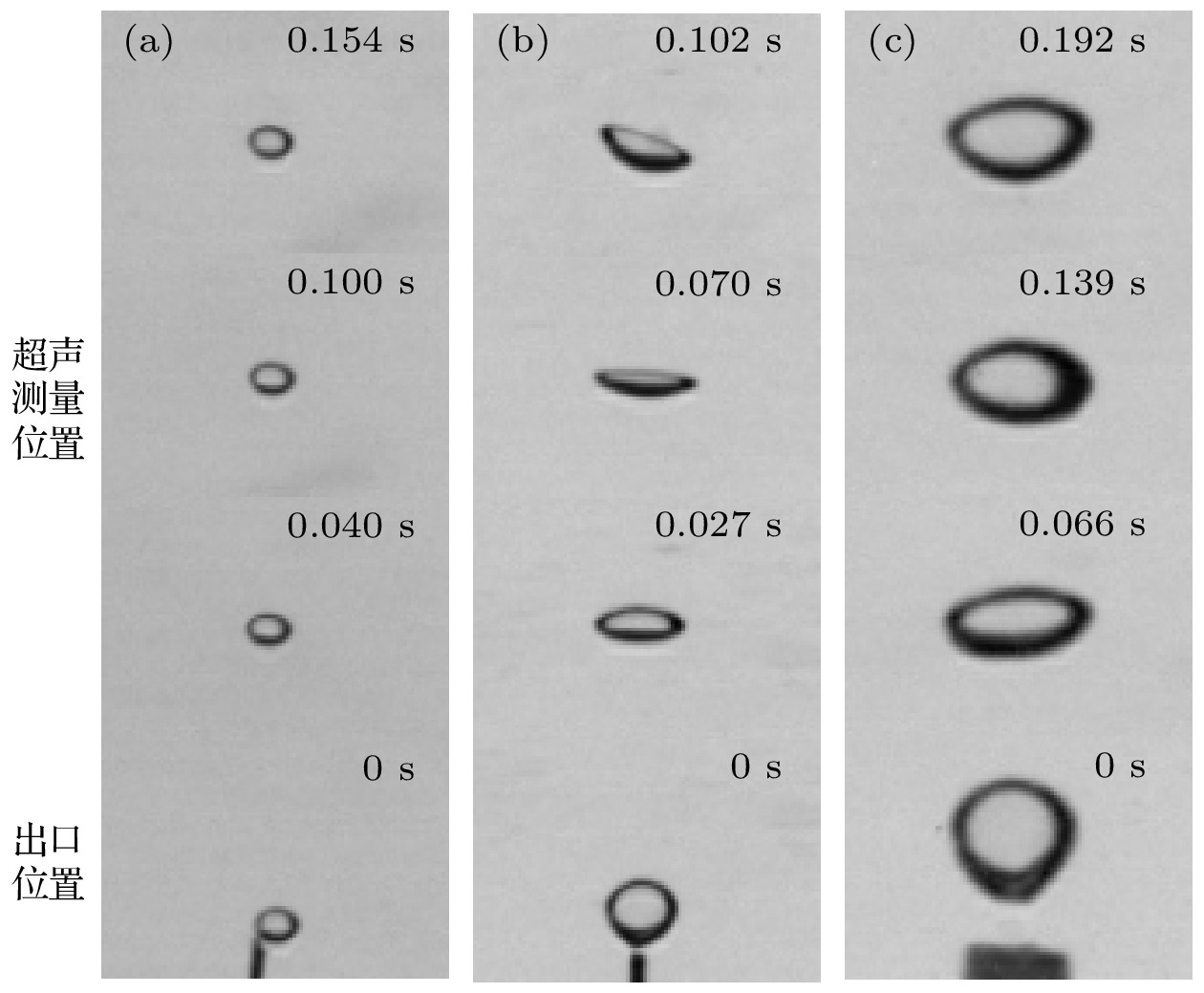
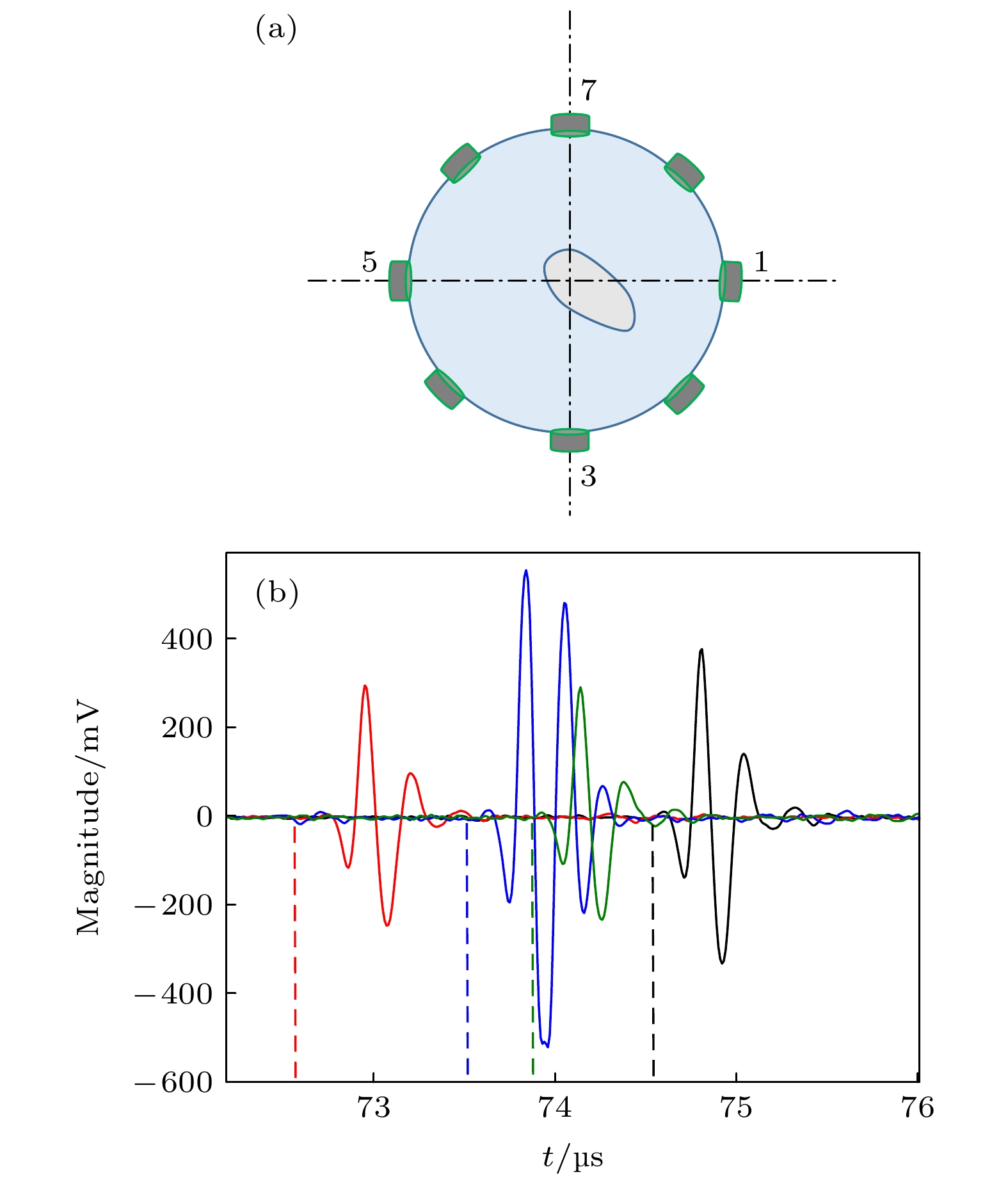
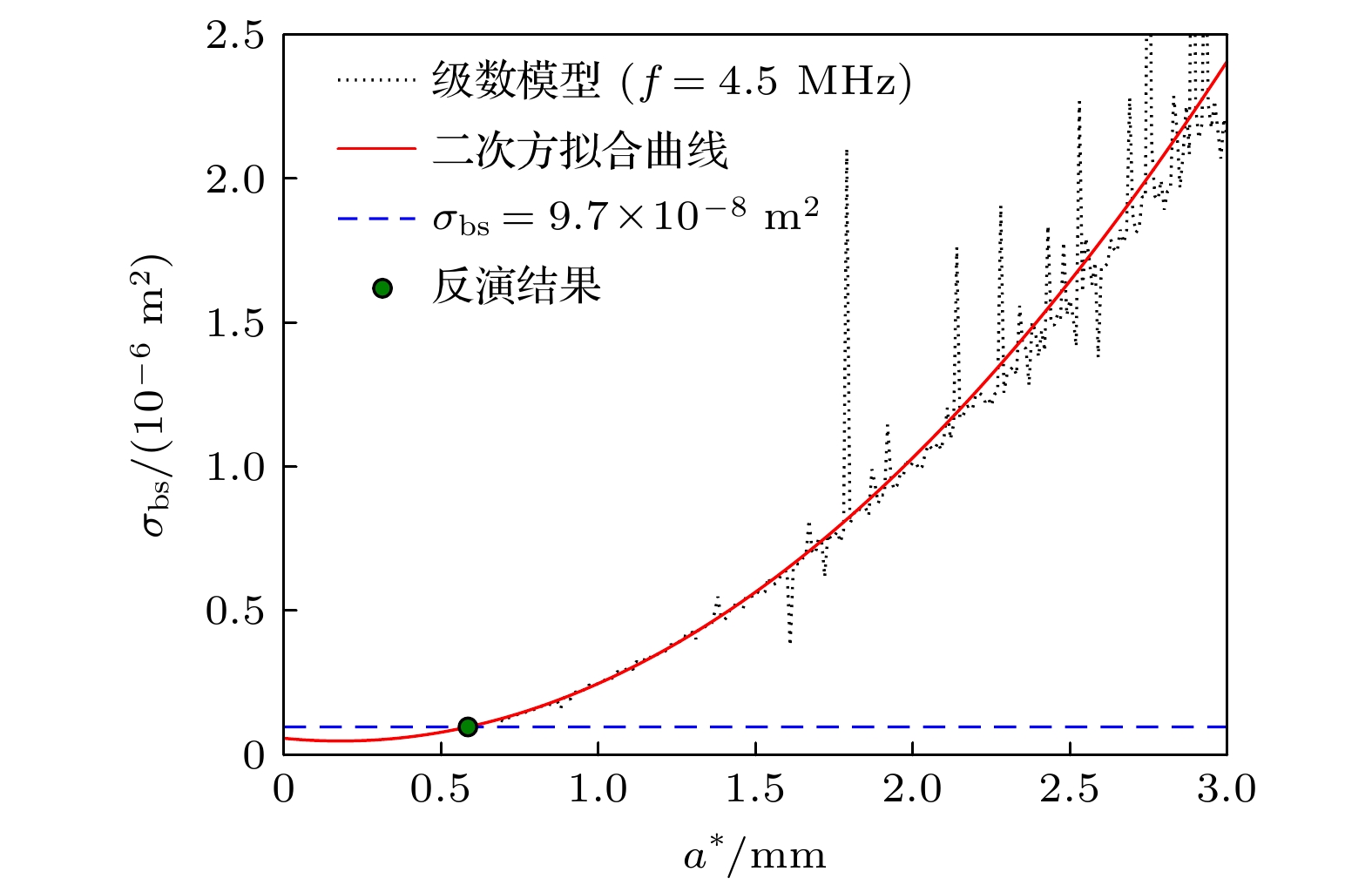
$ka\ll1 $ ) and Anderson (ka ≈ 1) models. The difference in scattering cross section σbs betweem them is only at the higher order formants of scattering, so the fitted line can be used to solve the multi-valued problem between σbs and ka. For a non-spherical bubble, σbs is determined by the frequency domain backscattering signal, the size is characterized by the equivalent radius a*, and the inversion is performed by fitted curve from series solution model. Ultrasonic quantitative results are examined by high-speed photography. Results show that during the bubbles rising along a zigzag path, they develop non-spherical bubbles, their scattering cross sections are measured by the frequency domain scattering signal obtained at a position of ultrasonic measurement, and the equivalent radius is inverted by the series solution fitting curve. The deviation of the result from the actual result r0 is about 1mm (relative error less than 45%) when 9≤kr0≤35. This method can be used for implementing the acoustic inversion of non-spherical bubbles in a certain range of measurement accuracy.-
Keywords:
- ultrasonic detection /
- scattering cross section /
- non-spherical bubbles /
- equivalent radius
[1] Leighton T G, Dogan H, Fox P, Mantouka A, Best A I, Robb G B R, White P R 2021 J. Acoust. Soc. Am. 150 2705
Google Scholar
[2] Judd A G, Hovland M, Dimitrov L I, García Gil S, Jukes V 2002 Geofluids 2 109
Google Scholar
[3] Kracht W, Moraga C 2016 Miner. Eng. 98 122
Google Scholar
[4] Liu J, Gao Q, Tang Z, Xie Y, Gui W, Ma T, Niyoyita J P 2020 IEEE Trans. Instrum. Meas. 69 9618
Google Scholar
[5] Guédra M, Inserra C, Gilles B 2017 Ultrason. Sonochem. 38 298
Google Scholar
[6] Buckey J C, Knaus D A, Alvarenga D L, Kenton M A, Magari P J 2005 Acta Astronaut. 56 1041
Google Scholar
[7] Wen W, Zong G H, Bi S S 2014 Rev. Sci. Instrum. 85 065106
Google Scholar
[8] Jarmo I, Tuomas E, Heikki M, Lasse L, Jari K, Heikki K 2014 19th Iberoamerican Congress Puerto Vallarta, Mexico Puerto Vallarta, Mexico, November 2−5, 2014 p38
[9] Ilonen J, Juránek R, Eerola T, Lensu L, Dubská M, Zemčík P, Kälviäinen H 2018 Pattern Recognit. Lett. 101 60
Google Scholar
[10] Ohta J, Doyama N, Wakabayashi D, Suzuki H 2013 T. Jpn. Soc. Mech. Eng. Part B 79 2397
Google Scholar
[11] Bradley P B, Seth J P 1992 Phys. Rev. Lett. 69 03839
Google Scholar
[12] Ren W, Jin N, Zhang J 2022 Ultrasonics 124 106740
Google Scholar
[13] Padilla A M, Loranger S, Kinnaman F S, Valentine D L, Weber T C 2019 J. Geophys. Res. Ocean. 124 2472
Google Scholar
[14] Padilla A M, Weber T C 2021 J. Acoust. Soc. Am. 149 2504
Google Scholar
[15] Clay C S, Medwin H 1977 Acoustical Oceanography: Principles and Applications (New York: Wiley) pp461–466
[16] Anderson V C 1950 J. Acoust. Soc. Am. 22 426
Google Scholar
[17] Zheng B L, Poojitha D Y M 2000 J. Hydraul. Eng. 126 852
Google Scholar
[18] Dong X, Su M, Cai X 2012 Particuology 10 117
Google Scholar
[19] Spiekhout S, Voorneveld J, van Elburg B, Renaud G, Segers T, Lajoinie G P R, Versluis M, Verweij M D, de Jong N, Bosch J G 2022 J. Acoust. Soc. Am. 151 3993
Google Scholar
[20] Sage K A, George J, Oberall H 1979 J. Acoust. Soc. Am. 65 1413
Google Scholar
[21] Sam A, Gomez C O, Finch J A 1996 Int. J. Miner. Process. 47 177
Google Scholar
[22] 郑晖, 林树青 2008 超声检测 (北京: 中国劳动社会保障社) 第75页
Zheng H, Lin S Q 2008 Ultrasonic Inspection (Beijing: China Labor and Social Security Publishing House) p75 (in Chinese)
[23] Weber T C, Ward L G 2015 J. Acoust. Soc. Am. 138 2169
Google Scholar
-
图 1 气泡测量装置(1-高速摄影机, 2-水槽, 3-流量控制阀, 4-进气口, 5-超声换能器, 6-声卡, 7-工控机)
Figure 1. Bubble measuring device. 1-high-speed camera, 2-tank, 3-flow control valves, 4-air inlet, 5-ultrasonic transducer, 6-sound card, 7-controller.
图 2 球形气泡散射模型
Figure 2. Scattering model of spherical bubble.
图 3 气泡散射模型对比 (a) 0.001≤ka≤1; (b) 1<ka≤50
Figure 3. Comparison of scattering models for bubbles: (a) 0.001≤ka≤1; (b) 1<ka≤50.
图 4 上升气泡的形态变化 (h = 120 mm) (a) r0 = 0.5 mm; (b) r0 = 1.3 mm; (c) r0 = 2.5 mm
Figure 4. Shape change of rising bubbles (h = 120 mm): (a) r0 = 0.5 mm; (b) r0 = 1.3 mm; (c) r0 = 2.5 mm.
图 5 气泡“之”字形上升轨迹 (a) r0 = 4.2 mm, h = 120, 160 mm; (b) r0 = 4.5 mm, h = 120, 160 mm; (c) r0 = 4.2 mm, h = 160 mm
Figure 5. Zigzag rising trajectory of the bubbles: (a) r0 = 4.2 mm, h = 120, 160 mm; (b) r0 = 4.5 mm, h = 120, 160 mm; (c) r0 = 4.2 mm, h = 160 mm.
图 6 自同一水深处上升气泡轨迹 (h = 120 mm) (a) r0 = 0.5 mm; (b) r0 = 1.3 mm; (c) r0 = 2.5 mm
Figure 6. Rising bubble trajectory with same depth (h = 120 mm): (a) r0 = 0.5 mm; (b) r0 = 1.3 mm; (c) r0 = 2.5 mm.
图 7 气泡散射时域信号及采集方法 (a)信号采集示意图; (b)不同角度的气泡时域散射信号
Figure 7. Time domain scattering signal of bubble and data acquisition method: (a) Schematic diagram of signal acquisition; (b) time domain scattering signals of bubbles at different angles.
图 8 频域散射信号(a)和散射截面校准因子(b)
Figure 8. Frequency domain scattering signal (a) and calibration factor of scattering cross section (b).
图 9 –6 dB带宽范围σbs测量结果
Figure 9. Measurements of σbs in the –6 dB bandwidth.
图 10 非球形气泡当量反演示意图
Figure 10. Inversion schematic for non-spherical bubbles.
图 11 超声与高速摄影定量结果对比
Figure 11. Comparison of quantitative results of ultrasound and high-speed camera.
表 1 测量位置处各泡的等效半径
$ r^* $ Table 1. Equivalent radius r* of each bubble at the measurement position.
r0/mm 0.5 1.0 1.3 2.5 3.2 4.2 4.5 4.8 5.5 r*/mm 0.5 1.1 1.4 2.4 3.2 4.6 4.4 4.9 5.9 χ 1.5 2.7 3.2 2.7 1.9 1.5 3.6 1.6 2.2 
DownLoad: CSV
表 2 测量位置处气泡的形状及形变率
Table 2. Shape and deformation rate of bubbles at the measurement position.
r0/mm 0.5 1.3 2.5 水平(χ*) 
竖直(χ)
DownLoad: CSV
-
[1] Leighton T G, Dogan H, Fox P, Mantouka A, Best A I, Robb G B R, White P R 2021 J. Acoust. Soc. Am. 150 2705
Google Scholar
[2] Judd A G, Hovland M, Dimitrov L I, García Gil S, Jukes V 2002 Geofluids 2 109
Google Scholar
[3] Kracht W, Moraga C 2016 Miner. Eng. 98 122
Google Scholar
[4] Liu J, Gao Q, Tang Z, Xie Y, Gui W, Ma T, Niyoyita J P 2020 IEEE Trans. Instrum. Meas. 69 9618
Google Scholar
[5] Guédra M, Inserra C, Gilles B 2017 Ultrason. Sonochem. 38 298
Google Scholar
[6] Buckey J C, Knaus D A, Alvarenga D L, Kenton M A, Magari P J 2005 Acta Astronaut. 56 1041
Google Scholar
[7] Wen W, Zong G H, Bi S S 2014 Rev. Sci. Instrum. 85 065106
Google Scholar
[8] Jarmo I, Tuomas E, Heikki M, Lasse L, Jari K, Heikki K 2014 19th Iberoamerican Congress Puerto Vallarta, Mexico Puerto Vallarta, Mexico, November 2−5, 2014 p38
[9] Ilonen J, Juránek R, Eerola T, Lensu L, Dubská M, Zemčík P, Kälviäinen H 2018 Pattern Recognit. Lett. 101 60
Google Scholar
[10] Ohta J, Doyama N, Wakabayashi D, Suzuki H 2013 T. Jpn. Soc. Mech. Eng. Part B 79 2397
Google Scholar
[11] Bradley P B, Seth J P 1992 Phys. Rev. Lett. 69 03839
Google Scholar
[12] Ren W, Jin N, Zhang J 2022 Ultrasonics 124 106740
Google Scholar
[13] Padilla A M, Loranger S, Kinnaman F S, Valentine D L, Weber T C 2019 J. Geophys. Res. Ocean. 124 2472
Google Scholar
[14] Padilla A M, Weber T C 2021 J. Acoust. Soc. Am. 149 2504
Google Scholar
[15] Clay C S, Medwin H 1977 Acoustical Oceanography: Principles and Applications (New York: Wiley) pp461–466
[16] Anderson V C 1950 J. Acoust. Soc. Am. 22 426
Google Scholar
[17] Zheng B L, Poojitha D Y M 2000 J. Hydraul. Eng. 126 852
Google Scholar
[18] Dong X, Su M, Cai X 2012 Particuology 10 117
Google Scholar
[19] Spiekhout S, Voorneveld J, van Elburg B, Renaud G, Segers T, Lajoinie G P R, Versluis M, Verweij M D, de Jong N, Bosch J G 2022 J. Acoust. Soc. Am. 151 3993
Google Scholar
[20] Sage K A, George J, Oberall H 1979 J. Acoust. Soc. Am. 65 1413
Google Scholar
[21] Sam A, Gomez C O, Finch J A 1996 Int. J. Miner. Process. 47 177
Google Scholar
[22] 郑晖, 林树青 2008 超声检测 (北京: 中国劳动社会保障社) 第75页
Zheng H, Lin S Q 2008 Ultrasonic Inspection (Beijing: China Labor and Social Security Publishing House) p75 (in Chinese)
[23] Weber T C, Ward L G 2015 J. Acoust. Soc. Am. 138 2169
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4213
- PDF Downloads: 90
- Cited By: 0
