Low-frequency sound insulation performance of novel membrane acoustic metamaterial with dynamic negative stiffness

Xu Qiang-Rong; Zhu Yang; Lin Kang; Shen Cheng; Lu Tian-Jian

doi:10.7498/aps.71.20221058

Abstract

For improving the low-frequency sound insulation properties of membrane/plate structures, a new quasi-zero stiffness membrane acoustic metamaterial with dynamic magnetic negative stiffness is proposed. When the equivalent magnetic charge theory is used to investigate the dynamic magnetic negative stiffness, a theoretical model of proposed metamaterial with finite dimension is established based on the Galerkin method. Through a combination of theoretical analysis, numerical simulation and experimental measurement, the low-frequency (1–1000 Hz) sound insulation performance of the metamaterial is investigated from several perspectives, including structural modality, vibration mode, average velocity, phase curve, equivalent mass density, and equivalent spring-mass dynamics model. The results show that at a certain initial membrane tension, the decreasing of the magnetic gap or the increasing of the residual flux density can increase the dynamic magnetic negative stiffness. This in turn leads the peak frequency to decrease and the bandwidth of sound insulation to increase, thus achieving effective low-frequency sound insulation over a wide frequency band. Further, when the magnetic gap is larger than the second critical magnetic gap and smaller than the first critical magnetic gap, the first-order modal resonance of the metamaterial disappears, and the corresponding value of sound insulation valley increases significantly, thus demonstrating superior sound insulation effect in a wide frequency band. The proposed method of using dynamic magnetic negative stiffness to improve low-frequency sound insulation valleys due to modal resonance provides useful theoretical guidance for designing membrane/plate type low-frequency sound insulation metamaterials.

Keywords:

Authors and contacts

1.
State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
2.
MIIT Key Laboratory of Multifunctional Lightweight Materials and Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Corresponding author: Shen Cheng, cshen@nuaa.edu.cn ; Lu Tian-Jian, tjlu@nuaa.edu.cn

Funds: Project supported by the Postgraduate Research and Practice Innovation Fund of Nanjing University of Aeronautics and Astronautics, China (Grant No. xcxjh20210106), the National Natural Science Foundation of China (Grant Nos. 11502110, 11972185), and the Open Fund of the State Key Laboratory for Strength and Vibration of Mechanical Structures, China (Grant No. SV2018-KF-01).

FullText HTML : translate this paragraph

References

[1]	Gao N S, Wu J G, Lu K, Zhong H B 2021 Mech. Syst. Sig. Process. 154 107504 Google Scholar
[2]	Kang Z X, Song R X, Zhang H J, Liu Q 2021 Appl. Acoust. 174 107785 Google Scholar
[3]	Ma G C, Sheng P 2016 Sci. Adv. 2 e1501595 Google Scholar
[4]	Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Sheng P 2012 Nat. Commun. 3 756 Google Scholar
[5]	Deng K, Ding Y Q, He Z J, Zhao H P, Shi J, Liu Z Y 2009 J. Appl. Phys. 105 124909 Google Scholar
[6]	Peng S S, He Z J, Jia H, Zhang A Q, Qiu C Y, Ke M Z, Liu Z Y 2010 Appl. Phys. Lett. 96 263502 Google Scholar
[7]	Zhu X F, Liang B, Kan W W, Zou X Y, Cheng J C 2011 Phys. Rev. Lett. 106 014301 Google Scholar
[8]	Liu Z Y, Zhang X, Mao Y, Zhu Y Y, Yang Z, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[9]	Kushwaha M S, Halevi P, Dobrzynski L, Djafari-Rouhani B 1993 Phys. Rev. Lett. 71 2022 Google Scholar
[10]	Gao N, Qu S C, Li J, Wang J, Chen W Q 2021 Int. J. Mech. Sci. 208 106695 Google Scholar
[11]	Nguyen H, Wu Q, Xu X C, Chen H, Tracy S, Huang G L 2020 Appl. Phys. Lett. 117 134103 Google Scholar
[12]	Demelofilho N G R, Claeys C, Deckers E, Desmet W 2020 Mech. Syst. Sig. Process. 139 106624 Google Scholar
[13]	Xiao Y, Wen J H, Wen X S 2012 J. Sound Vib. 331 5408 Google Scholar
[14]	Yang J, Lee J S, Lee H R, Kang Y J 2018 Appl. Phys. Lett. 112 091901 Google Scholar
[15]	Zhao X Z, Liu G Q, Zhang C, Xia D, Lu Z M 2018 Appl. Phys. Lett. 113 074101 Google Scholar
[16]	Wang X N, Zhou Y D, Sang J Q, Zhu W Y 2020 Appl. Acoust. 158 107045 Google Scholar
[17]	Lin Q H, Lin Q L, Wang Y H, Di G Q 2021 Compos. Struct. 273 114312 Google Scholar
[18]	Wang X L, Zhao H, Luo X D, Huang Z Y 2016 Appl. Phys. Lett. 108 041905 Google Scholar
[19]	Langfeldt F, Riecken J, Gleine W, von Estorff O 2016 J. Sound Vib. 373 1 Google Scholar
[20]	Langfeldt F, Kemsies H, Gleine W, von Estorff O 2017 Phys. Lett. A 381 1457 Google Scholar
[21]	Li Y L, Zhang Y L, Xie S C 2020 Appl. Acoust. 168 107427 Google Scholar
[22]	Xu Q S, Qiao J, Sun J Y, Zhang G Y, Li L Q 2021 J. Sound Vib. 493 115823 Google Scholar
[23]	Yang Z Y, Mei J, Yang M, Chan N H, Sheng P 2008 Phys. Rev. Lett. 101 204301 Google Scholar
[24]	Lu Z B, Yu X, Lau S K, Khoo B C, Cui F S 2020 Appl. Acoust. 157 107003 Google Scholar
[25]	Li X Y, Zhao J J, Wang W J, Xing T, Zhu L Y, Liu Y N, Li X H 2022 Appl. Acoust. 187 108514 Google Scholar
[26]	贺子厚, 赵静波, 姚宏, 陈鑫 2019 68 214302 Google Scholar He Z H, Zhao J B, Yao H, Chen X 2019 Acta Phys. Sin. 68 214302 Google Scholar
[27]	Naify C J, Chang C M, McKnight G, Nutt S 2011 J. Appl. Phys. 110 124903 Google Scholar
[28]	Tan X J, Wang B, Wang L C, Zhu S W, Chen S, Yao K L 2022 Compos. Struct. 286 115308 Google Scholar
[29]	Wang K, Zhou J X, Cai C Q, Xu D L, Ouyang H J 2019 Appl. Math. Modell. 73 581 Google Scholar
[30]	Yuan S J, Sun Y, Zhao J L, Meng K, Wang M, Pu H Y, Peng Y, Luo J, Xie S R 2020 J. Sound Vib. 482 115449 Google Scholar
[31]	胥强荣, 沈承, 韩峰, 卢天健 2021 70 244302 Google Scholar Xu Q R, Shen C, Han F, Lu T J 2021 Acta Phys. Sin. 70 244302 Google Scholar
[32]	Allag H, Yonnet J P 2009 Ieee. Trans. Magn. 45 3969 Google Scholar
[33]	Oyelade A O, Chen Y, Zhang R J, Hu G K 2018 Int. J. Appl. Mech. 10 1850054 Google Scholar
[34]	Wu J S, Luo S S 1997 J. Sound Vib. 200 179 Google Scholar
[35]	张光玉 2014 博士学位论文 (长沙: 国防科技大学) Zhang G Y 2014 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[36]	Meirovitch L 2001 Fundamentals of Vibrations (New York: McGraw-Hill Higher Education) pp529–530
[37]	Lee J H, Kim J 2002 J. Sound Vib. 251 349 Google Scholar

Cited By

图 1 准零刚度薄膜声学超材料结构　(a) 单胞模型; (b) xoy中面图; (c) yoz中面图; (d) 简化模型

Figure 1. Unit cell of quasi-zero stiffness membrane acoustic metamaterial (QZSMAMM): (a) Schematic of unit cell; (b) xoy mid-plane view; (c) yoz mid-plane view; (d) simplified model.

DownLoad: Full-Size Img PowerPoint

图 2 矩形磁铁的磁荷模型示意图

Figure 2. Schematic of the magnetic charge model for a cuboidal magnet.

DownLoad: Full-Size Img PowerPoint

图 3 (a) 磁间隙保持不变(H = 4.0 mm), 磁力负刚度随剩余磁通密度的变化; (b) 剩余磁通密度保持不变(B_r = 1.0 T), 磁力负刚度随磁间隙的变化

Figure 3. (a) Variation of negative magnetic stiffness with residual flux density at H = 4.0 mm; (b) variation of negative magnetic stiffness with magnetic gap at B_r = 1.0 T.

DownLoad: Full-Size Img PowerPoint

图 4 1000 Hz垂直入射声激励下, QZSMAMM的TL收敛性验证

Figure 4. Convergence check of theoretically predicted transmission loss (TL) of QZSMAMM under the excitation of a normally incident sound wave at 1000 Hz.

DownLoad: Full-Size Img PowerPoint

图 5 QZSMAMM的有限元模型

Figure 5. Finite element simulation model of QZSMAMM.

DownLoad: Full-Size Img PowerPoint

图 6 三组对照结构的理论和数值模拟传输损失对比

Figure 6. Comparison between theoretical model predictions and numerical simulation results of transmission loss for three different structures.

DownLoad: Full-Size Img PowerPoint

图 7 共振模态　(a) 无动态磁负刚度; (b) B_r = 1.0 T, H = 4.0 mm; (c) B_r = 1.0 T, H = 3.5 mm

Figure 7. Resonance mode: (a) Non-NS; (b) B_r = 1.0 T, H = 4.0 mm; (c) B_r = 1.0 T, H = 3.5 mm.

DownLoad: Full-Size Img PowerPoint

图 8 隔声峰/谷的振动模式　(a) 无动态磁负刚度; (b) B_r = 1.0 T, H = 4.0 mm; (c) B_r = 1.0 T, H = 3.5 mm

Figure 8. Vibration mode diagrams at sound insulation peak/valley: (a) Non-NS; (b) B_r = 1.0 T, H = 4.0 mm; (c) B_r = 1.0 T, H = 3.5 mm.

DownLoad: Full-Size Img PowerPoint

图 9 (a) 三组对照结构的传输损失和平均速度; (b) 三组对照结构的传输损失和相位变化

Figure 9. Curves of (a) transmission loss and average velocity and (b) transmission loss and phase change for three different structures.

DownLoad: Full-Size Img PowerPoint

图 11 隔声峰/谷的声压云图(单位: Pa)　(a) 无动态磁负刚度; (b) B_r = 1.0 T, H = 4.0 mm; (c) B_r = 1.0 T, H = 3.5 mm

Figure 11. Sound pressure cloud diagram at sound insulation peak/valley (unit: Pa): (a) Non-NS; (b) B_r = 1.0 T, H = 4.0 mm; (c) B_r = 1.0 T, H = 3.5 mm.

DownLoad: Full-Size Img PowerPoint

图 10 三组对照结构的传输损失和等效质量面密度曲线

Figure 10. Transmission loss and equivalent mass surface density curves of three different structures.

DownLoad: Full-Size Img PowerPoint

图 12 QZSMAMM的弹簧-质量等效模型

Figure 12. Spring-mass equivalent model of QZSMAMM.

DownLoad: Full-Size Img PowerPoint

图 13 剩余磁通密度保持不变(B_r = 1.0 T), 传输损失随磁间隙的变化

Figure 13. Variation of transmission loss with magnetic gap fixed at B_r = 1.0 T.

DownLoad: Full-Size Img PowerPoint

图 14 (a) 方位角$\varphi = {0^ \circ }$, 传输损失随入射角$\theta $的变化; (b) 入射角$\theta = {30^ \circ }$, 传输损失随入射角$\varphi $的变化

Figure 14. (a) Variation of transmission loss with incidence angle at $\varphi = {0^ \circ }$; (b) variation of transmission loss with azimuth at $\theta = {30^ \circ }$.

DownLoad: Full-Size Img PowerPoint

图 15 (a) 三种工况的传输损失对比(I: MAMM, II: QZSMAMM); (b) 三种工况的等效质量面密度对比(I: MAMM, II: QZSMAMM)

Figure 15. (a) Comparison of transmission loss curves among three working conditions (I: MAMM, II: QZSMAMM); (b) comparison of equivalent mass surface density curves among three working conditions (I: MAMM, II: QZSMAMM).

DownLoad: Full-Size Img PowerPoint

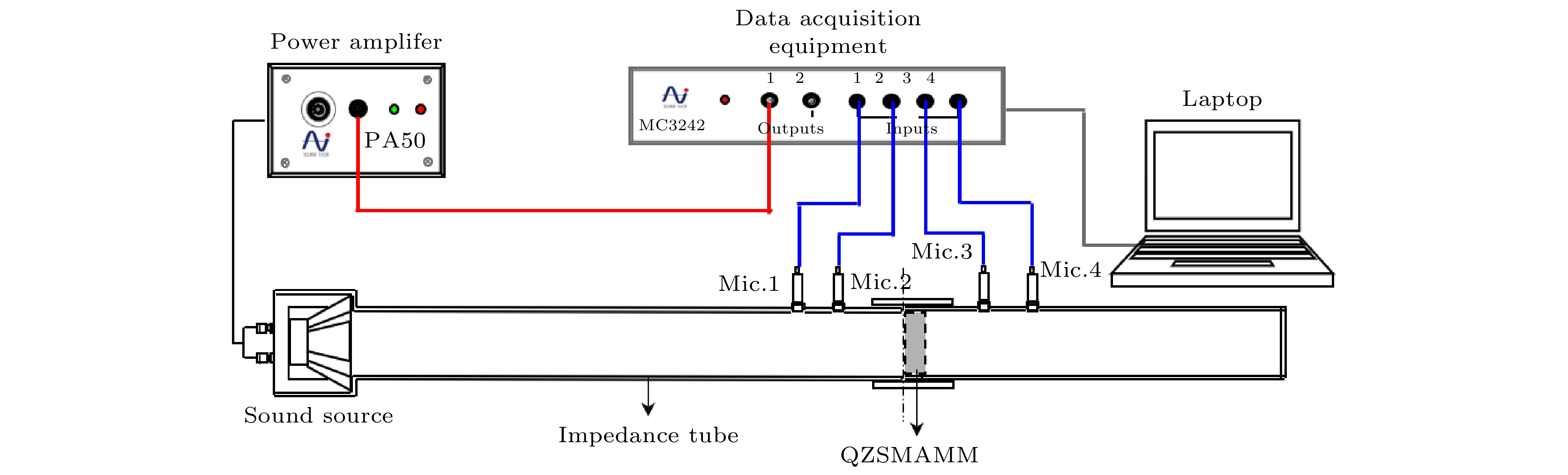
图 16 QZSMAMM单元的制备过程　(a) 施加薄膜张力; (b) 将中心贴敷有磁铁的张力薄膜粘接于支撑框架; (c) 添加外围磁铁; (d) 将样件置于阻抗管

Figure 16. Schematic of the preparation process of QZSMAMM unit: (a) Applying membrane tension; (b) tension membrane with a magnet applied to the center is bonded to the support frame; (c) adding peripheral magnets; (d) test sample positioned in impedance tube.

DownLoad: Full-Size Img PowerPoint

图 17 实验和有限元反演张力的传输损失对比

Figure 17. Comparison between experimentally measured and numerically predicted transmission loss versus frequency curves.

DownLoad: Full-Size Img PowerPoint

图 18 传输损失实验装置

Figure 18. Schematic of transmission loss experimental setup.

DownLoad: Full-Size Img PowerPoint

图 19 传输损失的实验测量与数值模拟对比

Figure 19. Comparison between experimentally measured and numerically predicted transmission loss versus frequency curves.

DownLoad: Full-Size Img PowerPoint

表 1 QZSMAMM单元几何参数和材料参数

Table 1. Geometric and material parameters of QZSMAMM unit.

L_x /mm	L_y /mm	l_x /mm	l_y /mm	t/mm	t₁/mm	B_r /T	T /(N·m^–1)	${\rho _{{\text{mem}}}}$ /(kg·m^–2)	${\rho _{{\text{mag}}}}$/(kg·m^–2)
40	40	5.32	5.32	0.2	2.0	1.0	500	0.24	15.6

DownLoad: CSV

表 2 理论和数值模拟的峰/谷频率

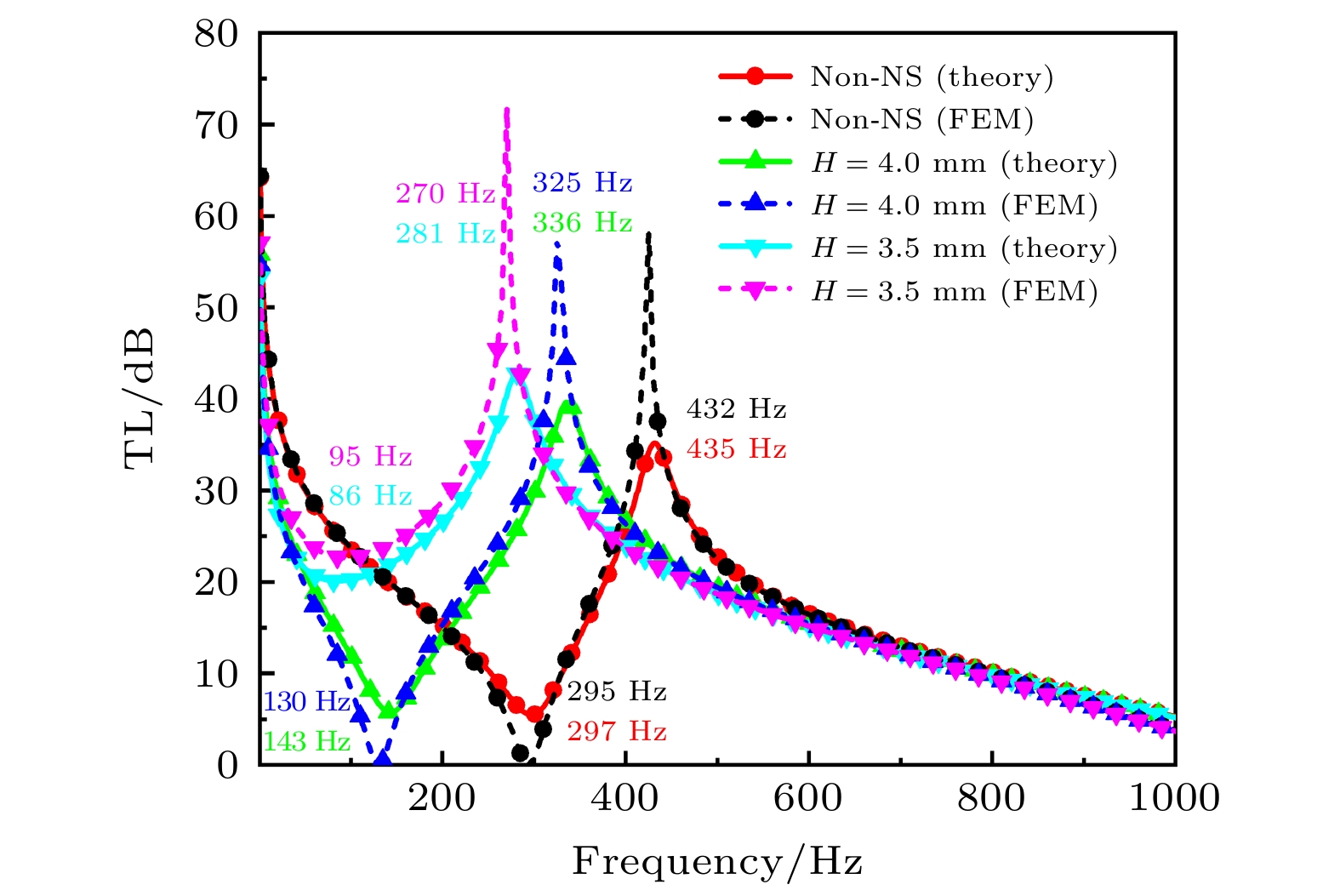
Table 2. Theoretical and numerical results for peak/valley frequencies.

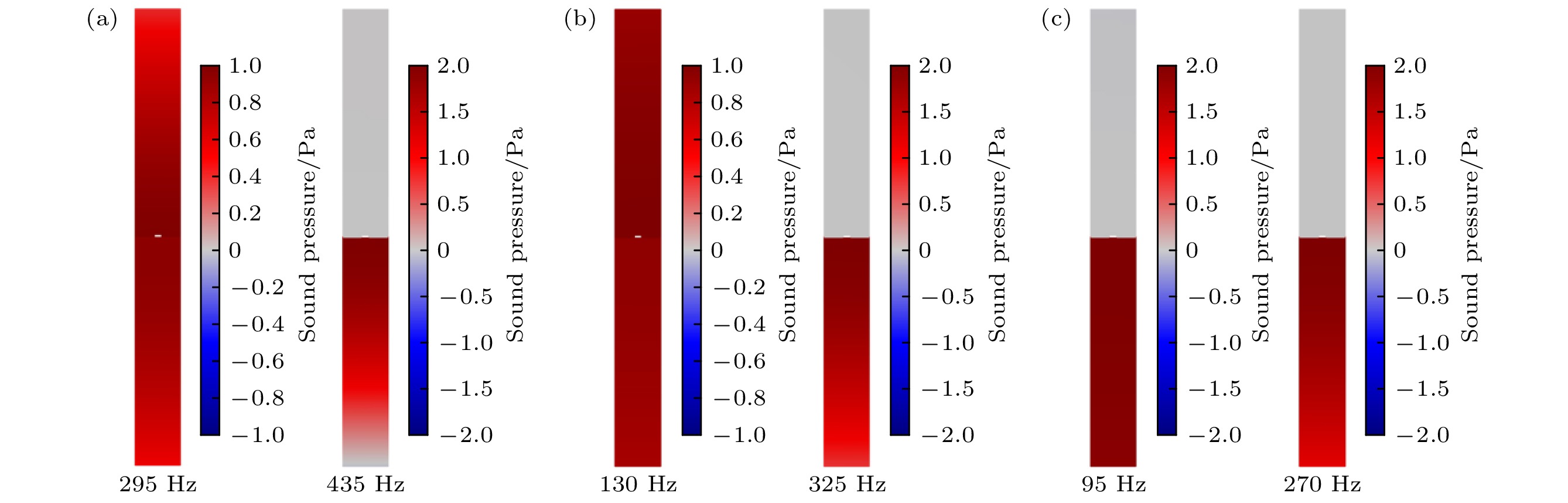
	Peak/valley frequency/Hz
	Non-NS	B_r = 1.0 T, H = 4.0 mm	B_r = 1.0 T, H = 3.5 mm
Theory	435/297	336/143	281/86
FEM	432/295	325/130	270/95

DownLoad: CSV

表 3 三种不同工况的结构参数和目标频率

Table 3. Structural parameters and target frequencies for three different operating conditions.

Configuration		T/(N·m^–1)	K_mag/(N·m^–1)	f/Hz
A	I	400	0	386
A	II	500	–670	386
B	I	200	0	274
B	II	400	–1300	274
C	I	50	0	138
C	II	200	–970	138

DownLoad: CSV

表 4 实验样件的相关材料参数

Table 4. Material parameters of experimental samples.

	Density/ (kg·m^–3)	Young’s modulus/GPa	Poisson ratio
Membrane	1200	1.8	0.38
Magnets	7594	200	0.29
Epoxy resin	1150	4.35	0.38

DownLoad: CSV

表 5 实验和数值模拟的峰/谷频率

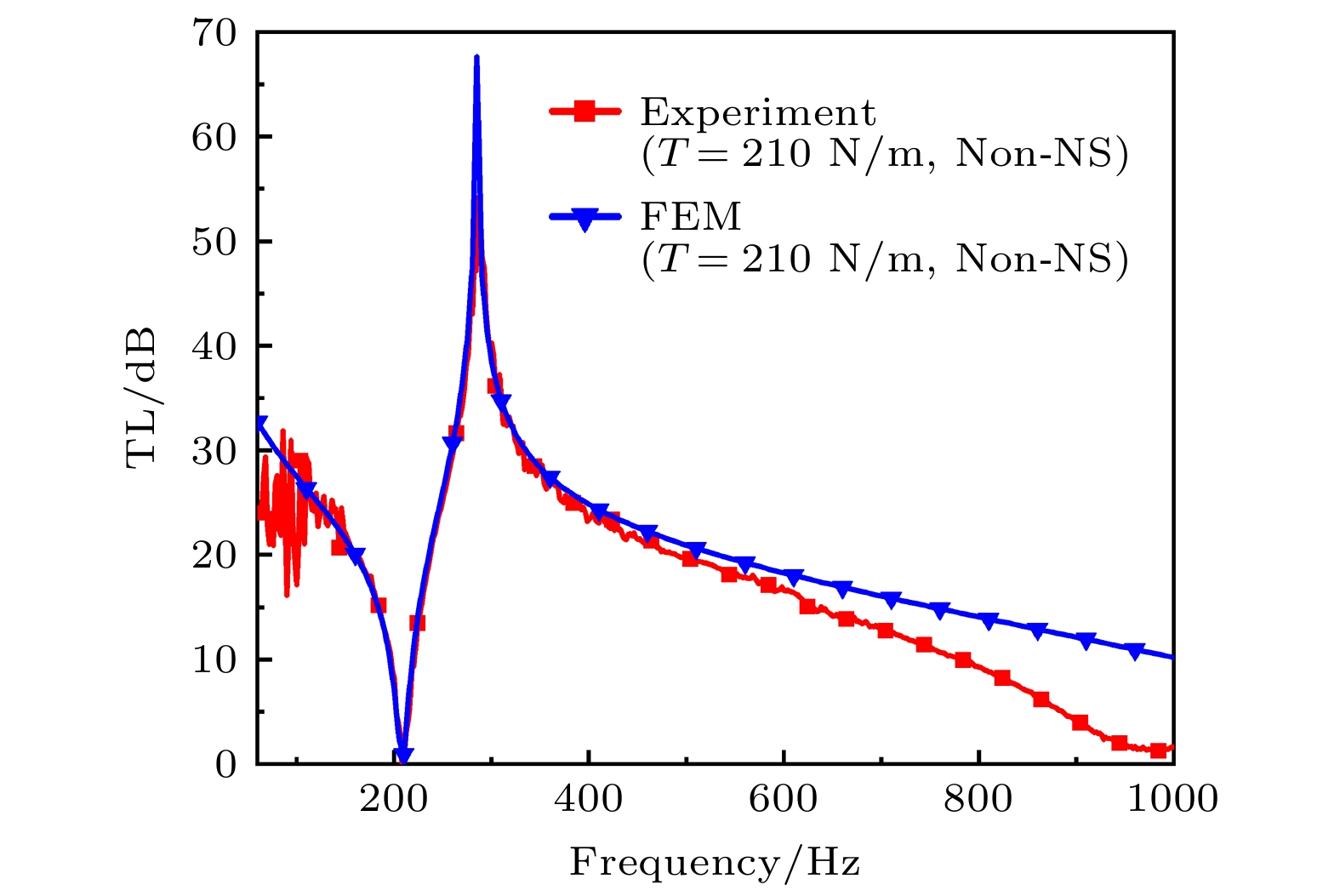
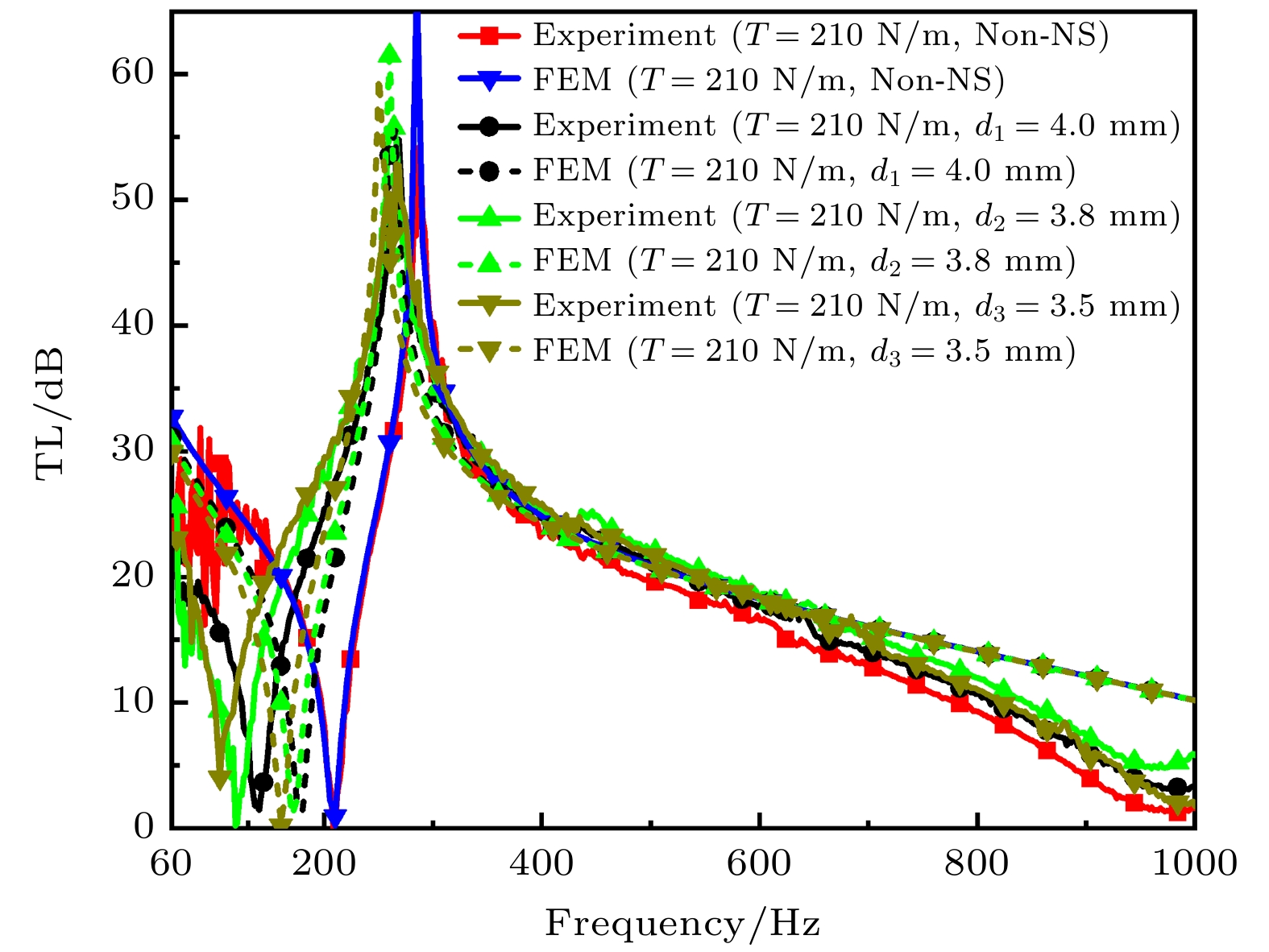
Table 5. Experimentally measured and numerically predicted peak/valley frequencies.

	Peak/valley frequency/Hz
	T = 210 N/m	T = 210 N/m	T = 210 N/m	T = 210 N/m
	T = 210 N/m	d₁ = 4.0 mm	d₂ = 3.8 mm	d₃ = 3.5 mm
Experiment	286/208	268/140	262/118	259/104
FEM	286/211	264/178	259/167	251/158

DownLoad: CSV

map

[1]	Gao N S, Wu J G, Lu K, Zhong H B 2021 Mech. Syst. Sig. Process. 154 107504 Google Scholar
[2]	Kang Z X, Song R X, Zhang H J, Liu Q 2021 Appl. Acoust. 174 107785 Google Scholar
[3]	Ma G C, Sheng P 2016 Sci. Adv. 2 e1501595 Google Scholar
[4]	Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Sheng P 2012 Nat. Commun. 3 756 Google Scholar
[5]	Deng K, Ding Y Q, He Z J, Zhao H P, Shi J, Liu Z Y 2009 J. Appl. Phys. 105 124909 Google Scholar
[6]	Peng S S, He Z J, Jia H, Zhang A Q, Qiu C Y, Ke M Z, Liu Z Y 2010 Appl. Phys. Lett. 96 263502 Google Scholar
[7]	Zhu X F, Liang B, Kan W W, Zou X Y, Cheng J C 2011 Phys. Rev. Lett. 106 014301 Google Scholar
[8]	Liu Z Y, Zhang X, Mao Y, Zhu Y Y, Yang Z, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[9]	Kushwaha M S, Halevi P, Dobrzynski L, Djafari-Rouhani B 1993 Phys. Rev. Lett. 71 2022 Google Scholar
[10]	Gao N, Qu S C, Li J, Wang J, Chen W Q 2021 Int. J. Mech. Sci. 208 106695 Google Scholar
[11]	Nguyen H, Wu Q, Xu X C, Chen H, Tracy S, Huang G L 2020 Appl. Phys. Lett. 117 134103 Google Scholar
[12]	Demelofilho N G R, Claeys C, Deckers E, Desmet W 2020 Mech. Syst. Sig. Process. 139 106624 Google Scholar
[13]	Xiao Y, Wen J H, Wen X S 2012 J. Sound Vib. 331 5408 Google Scholar
[14]	Yang J, Lee J S, Lee H R, Kang Y J 2018 Appl. Phys. Lett. 112 091901 Google Scholar
[15]	Zhao X Z, Liu G Q, Zhang C, Xia D, Lu Z M 2018 Appl. Phys. Lett. 113 074101 Google Scholar
[16]	Wang X N, Zhou Y D, Sang J Q, Zhu W Y 2020 Appl. Acoust. 158 107045 Google Scholar
[17]	Lin Q H, Lin Q L, Wang Y H, Di G Q 2021 Compos. Struct. 273 114312 Google Scholar
[18]	Wang X L, Zhao H, Luo X D, Huang Z Y 2016 Appl. Phys. Lett. 108 041905 Google Scholar
[19]	Langfeldt F, Riecken J, Gleine W, von Estorff O 2016 J. Sound Vib. 373 1 Google Scholar
[20]	Langfeldt F, Kemsies H, Gleine W, von Estorff O 2017 Phys. Lett. A 381 1457 Google Scholar
[21]	Li Y L, Zhang Y L, Xie S C 2020 Appl. Acoust. 168 107427 Google Scholar
[22]	Xu Q S, Qiao J, Sun J Y, Zhang G Y, Li L Q 2021 J. Sound Vib. 493 115823 Google Scholar
[23]	Yang Z Y, Mei J, Yang M, Chan N H, Sheng P 2008 Phys. Rev. Lett. 101 204301 Google Scholar
[24]	Lu Z B, Yu X, Lau S K, Khoo B C, Cui F S 2020 Appl. Acoust. 157 107003 Google Scholar
[25]	Li X Y, Zhao J J, Wang W J, Xing T, Zhu L Y, Liu Y N, Li X H 2022 Appl. Acoust. 187 108514 Google Scholar
[26]	贺子厚, 赵静波, 姚宏, 陈鑫 2019 68 214302 Google Scholar He Z H, Zhao J B, Yao H, Chen X 2019 Acta Phys. Sin. 68 214302 Google Scholar
[27]	Naify C J, Chang C M, McKnight G, Nutt S 2011 J. Appl. Phys. 110 124903 Google Scholar
[28]	Tan X J, Wang B, Wang L C, Zhu S W, Chen S, Yao K L 2022 Compos. Struct. 286 115308 Google Scholar
[29]	Wang K, Zhou J X, Cai C Q, Xu D L, Ouyang H J 2019 Appl. Math. Modell. 73 581 Google Scholar
[30]	Yuan S J, Sun Y, Zhao J L, Meng K, Wang M, Pu H Y, Peng Y, Luo J, Xie S R 2020 J. Sound Vib. 482 115449 Google Scholar
[31]	胥强荣, 沈承, 韩峰, 卢天健 2021 70 244302 Google Scholar Xu Q R, Shen C, Han F, Lu T J 2021 Acta Phys. Sin. 70 244302 Google Scholar
[32]	Allag H, Yonnet J P 2009 Ieee. Trans. Magn. 45 3969 Google Scholar
[33]	Oyelade A O, Chen Y, Zhang R J, Hu G K 2018 Int. J. Appl. Mech. 10 1850054 Google Scholar
[34]	Wu J S, Luo S S 1997 J. Sound Vib. 200 179 Google Scholar
[35]	张光玉 2014 博士学位论文 (长沙: 国防科技大学) Zhang G Y 2014 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[36]	Meirovitch L 2001 Fundamentals of Vibrations (New York: McGraw-Hill Higher Education) pp529–530
[37]	Lee J H, Kim J 2002 J. Sound Vib. 251 349 Google Scholar

[1]	Wei Wei, Guan Feng, Fang Xin. Integrated vibration absorption and isolation design method for metamaterial beams based on bandgap wave-insulating vibration isolatior. Acta Physica Sinica, 2024, 73(22): 224602. doi: 10.7498/aps.73.20241135
[2]	Li Ting, Wu Feng-Min, Zhang Tong-Tao, Wang Jun-Jun, Yang Bin, Zhang Dong. A low-frequency wideband ventilation muffler based on an embedded rough-necked Helmholtz resonator. Acta Physica Sinica, 2023, 72(22): 224301. doi: 10.7498/aps.72.20231047
[3]	Han Dong-Hai, Zhang Guang-Jun, Zhao Jing-Bo, Yao Hong. Low-frequency bandgaps and sound isolation characteristics of a novel Helmholtz-type phononic crystal. Acta Physica Sinica, 2022, 71(11): 114301. doi: 10.7498/aps.71.20211932
[4]	Xu Qiang-Rong, Shen Cheng, Han Feng, Lu Tian-Jian. Broadband low-frequency sound insulation performance of quasi-zero stiffness local resonant acoustic metamaterial plate. Acta Physica Sinica, 2021, 70(24): 244302. doi: 10.7498/aps.70.20211203
[5]	Shen Hui-Jie, Yu Dian-Long, Tang Zhi-Yin, Su Yong-Sheng, Li Yan-Fei, Liu Jiang-Wei. Characteristics of low-frequency noise elimination in a fluid-filled pipe of dark acoustic metamaterial type. Acta Physica Sinica, 2019, 68(14): 144301. doi: 10.7498/aps.68.20190311
[6]	Zhai Shi-Long, Wang Yuan-Bo, Zhao Xiao-Peng. A kind of tunable acoustic metamaterial for low frequency absorption. Acta Physica Sinica, 2019, 68(3): 034301. doi: 10.7498/aps.68.20181908
[7]	He Zi-Hou, Zhao Jing-Bo, Yao Hong, Jiang Juan-Na, Chen Xin. Sound insulation performance of thin-film acoustic metamaterials based on piezoelectric materials. Acta Physica Sinica, 2019, 68(13): 134302. doi: 10.7498/aps.68.20190245
[8]	He Zi-Hou, Zhao Jing-Bo, Yao Hong, Chen Xin. Sound insulation performance of Helmholtz cavity with thin film bottom. Acta Physica Sinica, 2019, 68(21): 214302. doi: 10.7498/aps.68.20191131
[9]	Wang Yue, Leng Yan-Bing, Wang Li, Dong Lian-He, Liu Shun-Rui, Wang Jun, Sun Yan-Jun. Tunable grapheme amplitude based broadband electromagnetically-induced-transparency-like metamaterial. Acta Physica Sinica, 2018, 67(9): 097801. doi: 10.7498/aps.67.20180114
[10]	Liu Song, Luo Chun-Rong, Zhai Shi-Long, Chen Huai-Jun, Zhao Xiao-Peng. Inverse Doppler effect of acoustic metamaterial with negative mass density. Acta Physica Sinica, 2017, 66(2): 024301. doi: 10.7498/aps.66.024301
[11]	Gao Dong-Bao, Liu Xuan-Jun, Tian Zhang-Fu, Zhou Ze-Min, Zeng Xin-Wu, Han Kai-Feng. A broadband low-frequency sound insulation structure based on two-dimensionally inbuilt Helmholtz resonator. Acta Physica Sinica, 2017, 66(1): 014307. doi: 10.7498/aps.66.014307
[12]	Zhang Yong-Yan, Wu Jiu-Hui, Zhong Hong-Min. Low-frequency wide-band mechanism of a new type acoustic metamaterial with negative modulus. Acta Physica Sinica, 2017, 66(9): 094301. doi: 10.7498/aps.66.094301
[13]	Si Li-Ming, Hou Ji-Xuan, Liu Yong, Lü Xin. Active tunable metamaterial transmission line based on lumped elements and negative differencial devices. Acta Physica Sinica, 2014, 63(2): 027802. doi: 10.7498/aps.63.027802
[14]	Ma Xi-Yue, Chen Ke-An, Ding Shao-Hu, Zhang Bing-Rui. Optimization of piezoelectric sensor arrays in error sensing of active triple sound insulation structure. Acta Physica Sinica, 2013, 62(12): 124301. doi: 10.7498/aps.62.124301
[15]	Xu Yang-Qiu, Zhang Hui-Bin, Zhou Pei-Heng, Lu Hai-Peng, Liang Di-Fei, Xie Jian-Liang. Design of a low-frequency broadband circuit analog absorbers based on wire media. Acta Physica Sinica, 2013, 62(5): 058103. doi: 10.7498/aps.62.058103
[16]	Wang Ying, Cheng Yong-Zhi, Nie Yan, Gong Rong-Zhou. Design and experiments of low-frequency broadband metamaterial absorber based on lumped elements. Acta Physica Sinica, 2013, 62(7): 074101. doi: 10.7498/aps.62.074101
[17]	Shen Hui-Jie, Wen Ji-Hong, Yu Dian-Long, Cai Li, Wen Xi-Sen. Research on a cylindrical cloak with active acoustic metamaterial layers. Acta Physica Sinica, 2012, 61(13): 134303. doi: 10.7498/aps.61.134303
[18]	Cheng Yong-Zhi, Wang Ying, Nie Yan, Zheng Dong-Hao, Gong Rong-Zhou, Xiong Xuan, Wang Xian. Design of a low-frequency broadband metamaterial absorber based on resistance frequency selective surface. Acta Physica Sinica, 2012, 61(13): 134102. doi: 10.7498/aps.61.134102
[19]	Ding Chang-Lin, Zhao Xiao-Peng. Audible sound metamaterial. Acta Physica Sinica, 2009, 58(9): 6351-6355. doi: 10.7498/aps.58.6351
[20]	Wang Lian-Sheng, Luo Chun-Rong, Huang Yong, Zhao Xiao-Peng. Electrically tunable negative permeability metamaterials based on electrorheological fluids. Acta Physica Sinica, 2008, 57(6): 3571-3577. doi: 10.7498/aps.57.3571

Catalog

Vol. 71, Issue 21 - 2022-11-05

Metrics

Abstract views: 4457
PDF Downloads: 115
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板