Broadband low-frequency sound insulation performance of quasi-zero stiffness local resonant acoustic metamaterial plate

Xu Qiang-Rong; Shen Cheng; Han Feng; Lu Tian-Jian

doi:10.7498/aps.70.20211203

Abstract

For realizing the effective broadband insulation of sound at low frequencies, a novel local resonant acoustic metamaterial plate having quasi-zero stiffness is proposed. Based on the classical mass-spring local resonance model, a metastructure is constructed by introducing additional inclined springs with negative stiffness. First, the normalized equivalent stiffness of the quasi-zero stiffness structure is derived from the perspective of dynamics. Then, by employing the method of equivalent medium, a sound insulation model of the metastructure is established theoretically. For validation, numerical simulations as well as experimental measurements are carried out. It is demonstrated that in the positive (equivalent) stiffness regime, increasing either the stiffness ratio or pre-compression can significantly reduce the local resonance frequency of the metastructure, which exhibits the great insulation performance around the local resonance frequency. For a typical example, the proposed metastructure can achieve a transmission loss of 30 dB around 10 Hz. In contrast, within the negative stiffness regime, the metastructure does not exhibit local resonance, thus avoiding sound insulation valley caused by the “coincidence effect”. Compared with traditional materials or similar metamaterials, the proposed metastructure has significant advantages in sound insulation (e.g. more than 30 dB drop over a wide frequency band of 53－1500 Hz). By analyzing the equivalent mass density, reflection coefficient, and acoustic impedance ratio of the metastructure, the physical mechanism behind its superior insulation performance is further explored. The equivalent mass density changes from positive to negative and tends to infinity at the insulation peak. The insulation peak is attributed to a nearly perfect total reflection of sound wave caused by impedance mismatch, while the insulation valley is caused by low-frequency “coincidence effect” originating from the local resonance band gap. The using of the quasi-zero stiffness local resonance to achieve low-frequency broadband sound insulation overcomes the disadvantages of traditional metamaterials such as reduced stiffness or additional mass, thus becoming vastly attractive for constructing low-frequency broad band sound insulation structures.

Keywords:

Authors and contacts

1.
State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
2.
State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China
3.
Department of Function and Structure, Shanghai Aircraft Design and Research Institute, Shanghai 201210, China

Corresponding author: Shen Cheng, cshen@nuaa.edu.cn ; Lu Tian-Jian, tjlu@nuaa.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11502110, 11972185) and the Open Fund of the State Key Laboratory for Strength and Vibration of Mechanical Structures, China (Grant No. SV2018-KF-01).

FullText HTML : translate this paragraph

References

[1]	田源, 葛浩, 卢明辉, 陈延锋 2019 68 194301 Google Scholar Tian Y, Ge H, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 194301 Google Scholar
[2]	Ma G C, Sheng P 2016 Sci. Adv. 2 e1501595 Google Scholar
[3]	丁昌林, 董仪宝, 赵晓鹏 2018 67 194301 Google Scholar Ding C L, Dong Y B, Zhao X P 2018 Acta Phys. Sin. 67 194301 Google Scholar
[4]	Liu Z Y, Chan C T, Sheng P 2005 Phys. Rev. B 71 014103 Google Scholar
[5]	Fang N, Xi D J, Xu J Y, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452 Google Scholar
[6]	Deng K, Ding Y Q, He Z J, Zhao H P, Shi J, Liu Z Y 2009 J. Appl. Phys. 105 188505 Google Scholar
[7]	Zhu X F, Liang B, Kan W W, Zou X Y, Cheng J C 2011 Phys. Rev. Lett. 106 014301 Google Scholar
[8]	Peng S S, He Z J, Jia H, Zhang A Q, Qiu C Y, Ke M Z, Liu Z Y 2010 Appl. Phys. Lett. 96 263502 Google Scholar
[9]	Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Sheng P 2012 Nat. Commun. 3 756 Google Scholar
[10]	Kushwaha M S, Halevi P, Dobrzynski L, Djafari-Rouhani B 1993 Phys. Rev. Lett. 71 2022 Google Scholar
[11]	Liu Z Y, Zhang X, Mao Y, Zhu Y Y, Yang Z, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[12]	张佳龙, 姚宏, 杜军, 赵静波, 董亚科, 祁鹏山 2016 硅酸盐学报 44 1440 Google Scholar Zhang J L, Yao H, Du J, Zhao J B, Dong Y K, Qi P S 2016 J. Chin. Ceramic Soc. 44 1440 Google Scholar
[13]	张思文, 吴九汇 2013 62 134302 Google Scholar Zhang S W, Wu J H 2013 Acta Phys. Sin. 62 134302 Google Scholar
[14]	张永燕, 吴九汇, 钟宏民 2017 66 094301 Google Scholar Zhang Y Y, Wu J H, Zhong H M 2017 Acta Phys. Sin. 66 094301 Google Scholar
[15]	张若军, 肖勇, 温激鸿, 郁殿龙 2016 振动工程学报 29 905 Google Scholar Zhang R J, Xiao Y, Wen J H, Yu D L 2016 J. Vib. Eng. 29 905 Google Scholar
[16]	乔厚, 何锃, 张恒堃, 彭伟才, 江雯 2019 68 128101 Google Scholar Qiao H, He Z, Zhang H K, Peng W C, Jiang W 2019 Acta Phys. Sin. 68 128101 Google Scholar
[17]	梅军, 杨旻, 杨志宇, 陈傲轩, 沈平 2010 物理 39 243 Mei J, Yang M, Yang Z Y, Chen A X, Shen P 2010 Physics 39 243
[18]	贺子厚, 赵静波, 姚宏, 陈鑫 2019 68 214302 Google Scholar He Z H, Zhao J B, Yao H, Chen X 2019 Acta Phys. Sin. 68 214302 Google Scholar
[19]	贺子厚, 赵静波, 姚宏, 蒋娟娜, 陈鑫 2019 68 134302 Google Scholar He Z H, Zhao J B, Yao H, Jiang J N, Chen X 2019 Acta Phys. Sin. 68 134302 Google Scholar
[20]	Xiao Y, Wen J H, Wen X S 2012 J. Phys. D:Appl. Phys. 45 195401 Google Scholar
[21]	Xiao Y, Wen J H, Wen X S 2012 J. Sound Vib. 331 5408 Google Scholar
[22]	Huang X C, Liu X T, Sun J Y, Zhang Z Y, Hua H X 2014 J. Sound Vib. 333 1132 Google Scholar
[23]	Carrella A, Brennan M J, Waters T P 2007 J. Sound Vib. 301 678 Google Scholar
[24]	Zheng Y S, Zhang X N, Luo Y J, Zhang Y H, Xie S L 2018 Mech. Syst. Sig. Process. 100 135 Google Scholar
[25]	Wang K, Zhou J X, Cai C Q, Xu D L, Ouyang H J 2019 Appl. Math. Modell. 73 581 Google Scholar
[26]	张浩 2016 博士学位论文 (长沙: 国防科技大学) Zhang H 2016 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[27]	杜功焕, 朱哲民, 龚秀芬 2012 声学基础 (南京: 南京大学出版社) 第71页 Du G H, Zhu Z M, Gong X F 2012 Acoustic Basis (Nanjing: Nanjing University Press) p71 (in Chinese)
[28]	李佩 2014 博士学位论文 (北京: 北京理工大学) Li P 2014 Ph. D. Dissertation (Beijing: Beijing Institute of Technology) (in Chinese)
[29]	何琳, 朱海潮, 邱小军, 杜功焕 2006 声学理论与工程应用 (北京: 科学出版社) 第177页 He L, Zhu H C, Qiu X J, Du G H 2006 Acoustic Theory and Engineering Application (Beijing: Science Press) p177 (in Chinese)

Cited By

图 1 准零刚度局域共振结构^[25]　(a)结构示意图; (b)单胞结构; (c)主要几何参数; (d)准零刚度单元俯视图

Figure 1. Quasi-zero stiffness local resonance structure^[25]: (a) Schematic of whole structure; (b) unit cell; (c) main geometric parameters; (d) top view of quasi-zero stiffness element.

DownLoad: Full-Size Img PowerPoint

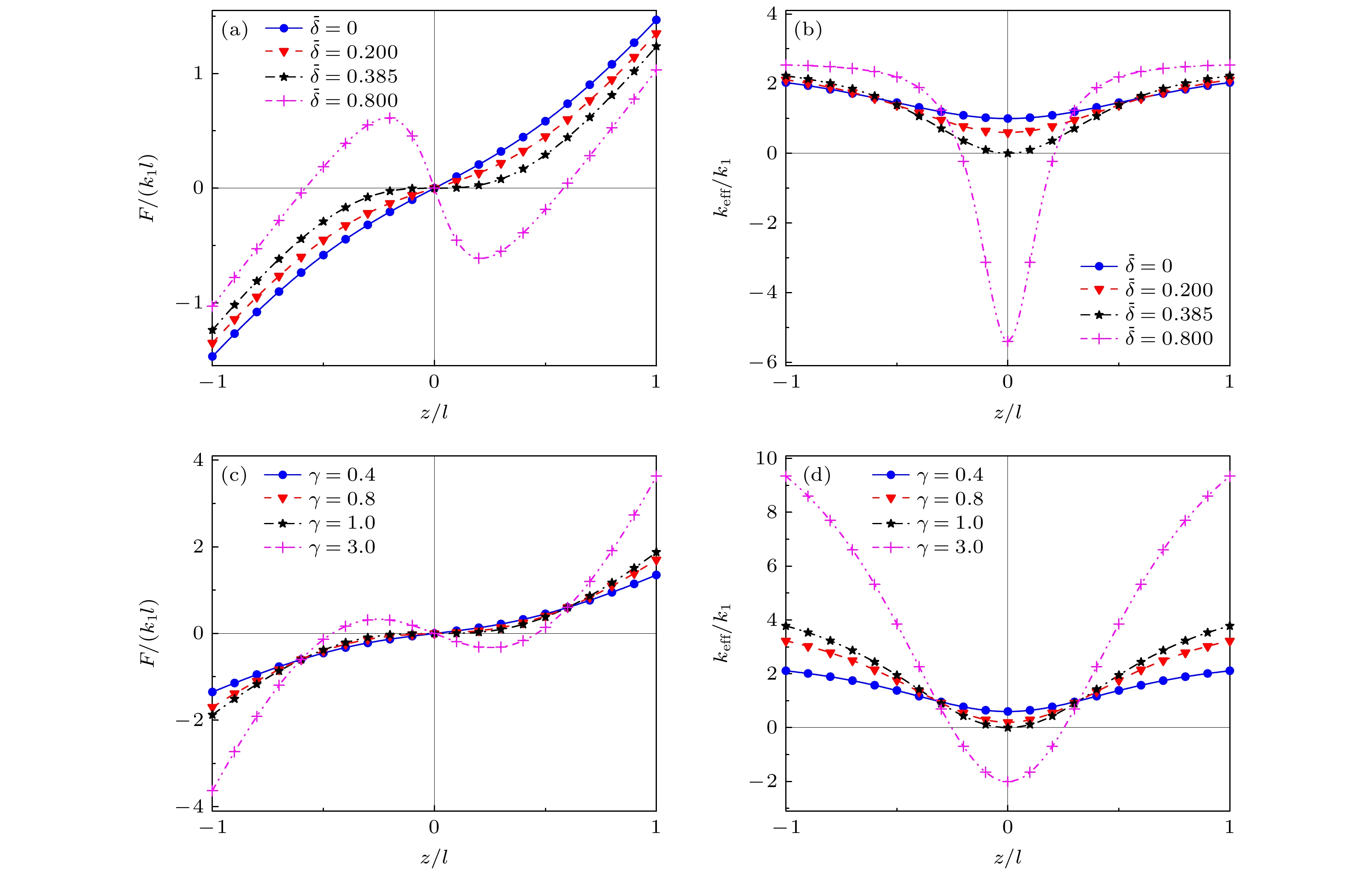
图 2 弹簧刚度比保持不变($\gamma = 0.4$), (a)归一化恢复力和(b)等效刚度随弹簧预压缩量的变化趋势; 弹簧预压缩量保持不变($\bar \delta = 0.2$), (c)归一化恢复力和(d)等效刚度随弹簧刚度比的变化趋势

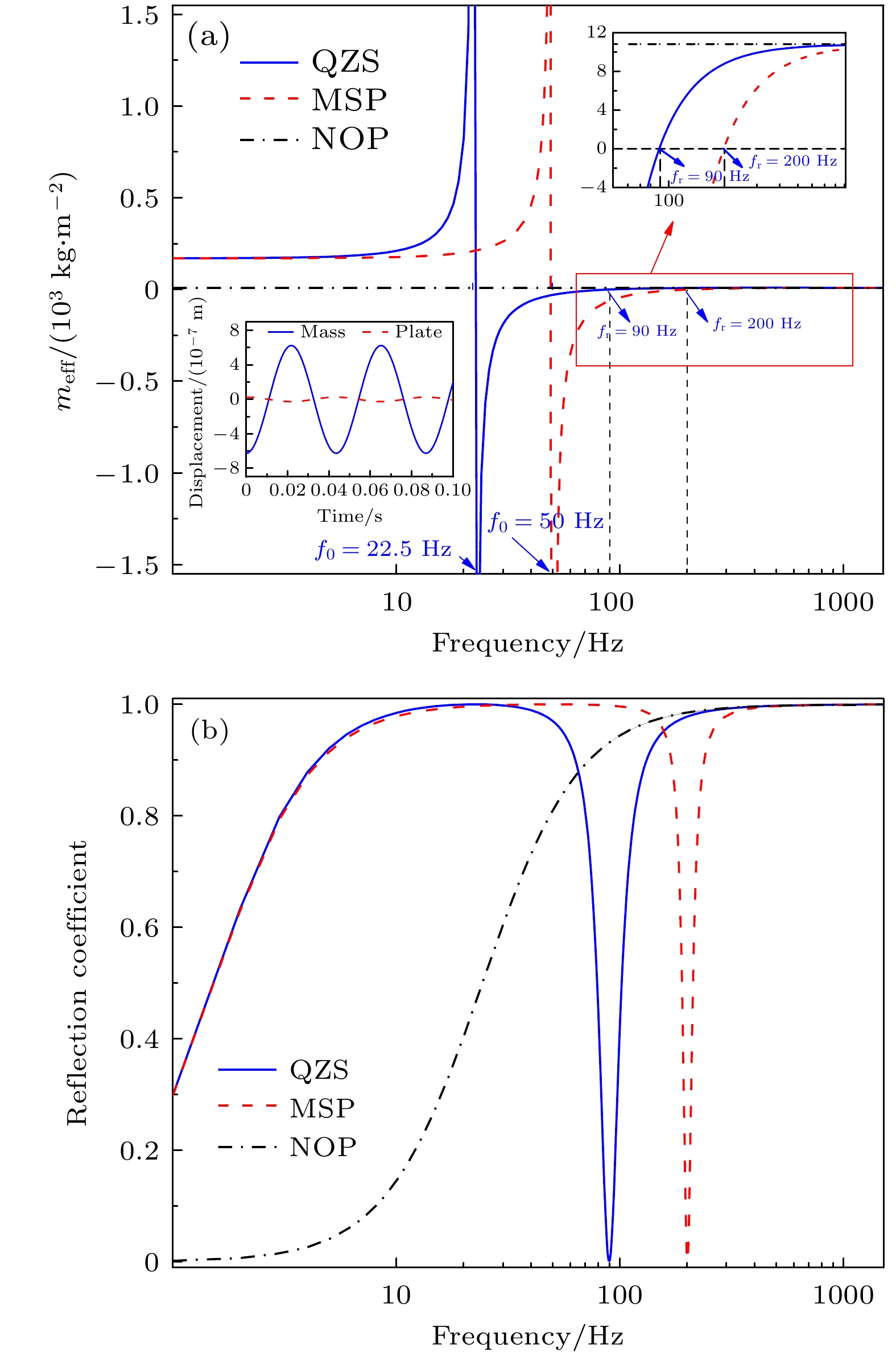
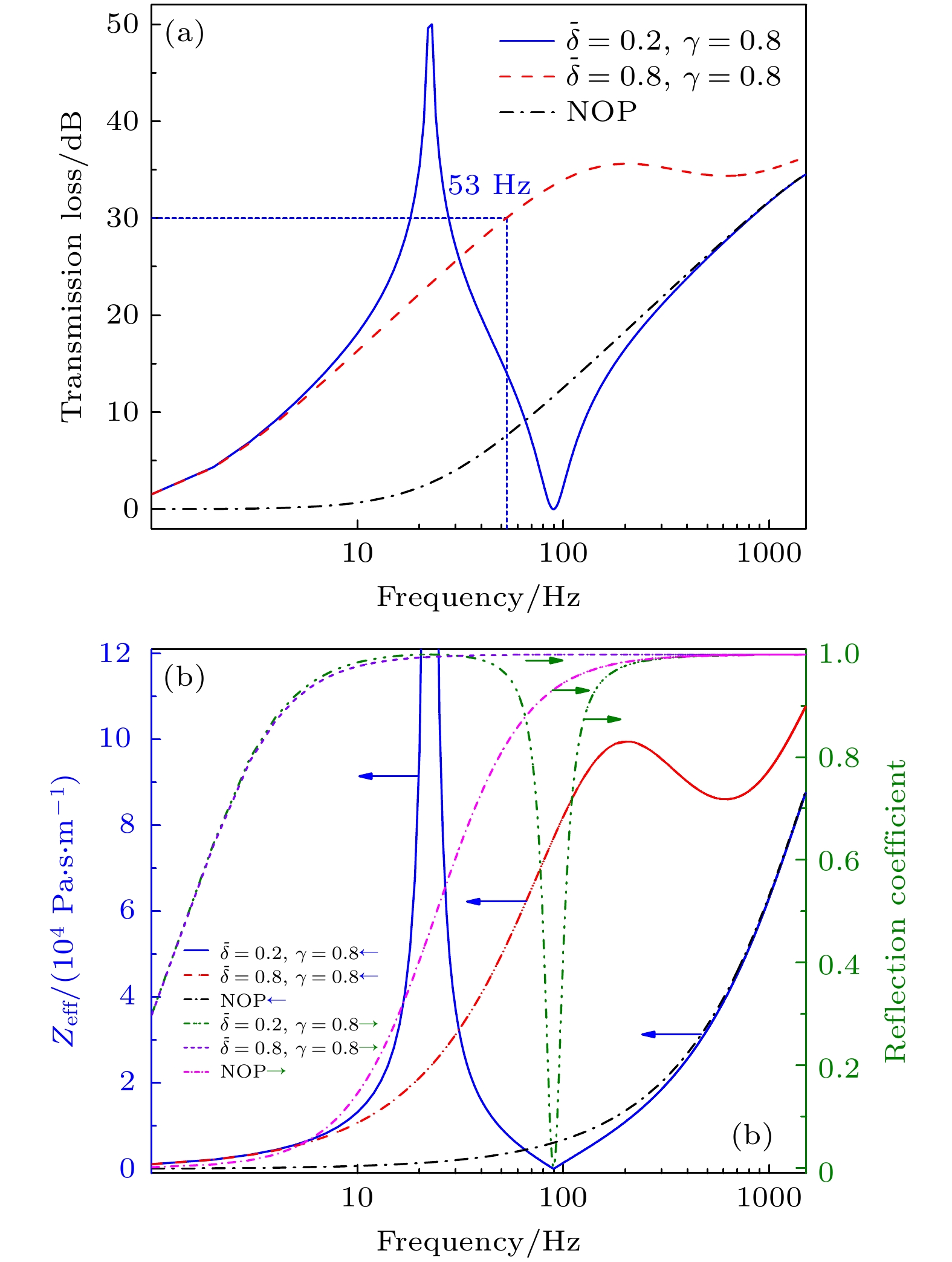
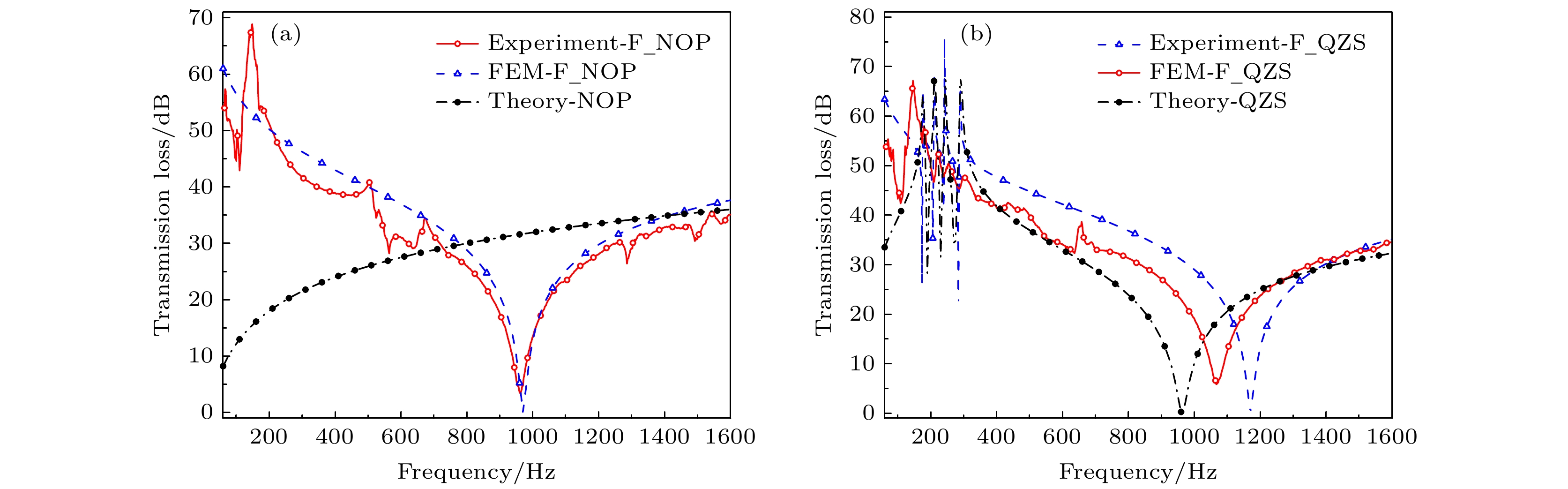
Figure 2. (a) Normalized reacting force and (b) equivalent stiffness plotted as functions of pre-compression of springs for $\gamma = 0.4$; (c) normalized reacting force and (d) equivalent stiffness plotted as functions of spring stiffness ratio for $\bar \delta = 0.2$.

DownLoad: Full-Size Img PowerPoint

图 3 周期性元胞有限元模型　(a)有限元模型; (b)集总机械系统原理图

Figure 3. Finite element model of periodic cell: (a) Finite element model; (b) schematic diagram of lumped mechanical system.

DownLoad: Full-Size Img PowerPoint

图 4 三种声学板结构的传输损失: 理论预测与数值模拟对比

Figure 4. Comparison of sound transmission loss among three different plate structures: Analytical model prediction versus numerical simulation.

DownLoad: Full-Size Img PowerPoint

图 5 三种板结构对比　(a)等效质量面密度和超材料板的偶极子振动模式; (b)反射系数

Figure 5. Comparison among three different plate structures: (a) Equivalent mass surface density and dipole vibration mode of QZS; (b) reflection coefficient.

DownLoad: Full-Size Img PowerPoint

图 6 声压云图(单位: Pa)　(a) 22.5 Hz; (b) 90 Hz

Figure 6. Sound pressure cloud diagram (unit: Pa): (a) 22.5 Hz; (b) 90 Hz.

DownLoad: Full-Size Img PowerPoint

图 7 正刚度区传输损失对比　(a)刚度比的影响($\bar \delta = $$ 0.2$); (b)预压缩量的影响($\gamma = 0.4$)

Figure 7. Comparison of transmission loss versus frequency curves in positive equivalent stiffness zone: (a) Influence of stiffness ratio at $\bar \delta = 0.2$; (b) influence of pre-compression at $\gamma = 0.4$.

DownLoad: Full-Size Img PowerPoint

图 8 负刚度区传输损失对比

Figure 8. Comparison of transmission loss versus frequency curves in negative equivalent stiffness zone.

DownLoad: Full-Size Img PowerPoint

图 9 正/负等效刚度区超材料板和无振子板对比　(a)传输损失; (b)等效阻抗和反射系数

Figure 9. Metamaterial plate compared with non-oscillator plate in both positive regime ($\bar \delta = 0.2$ and $\gamma = 0.8$) and negative regime ($\bar \delta = 0.8$ and $\gamma = 0.8$) of equivalent stiffness: (a) Transmission loss; (b) equivalent impedance and reflection coefficient.

DownLoad: Full-Size Img PowerPoint

图 10 传输损失随入射角变化曲线

Figure 10. Comparison of transmission loss under different incident angle.

DownLoad: Full-Size Img PowerPoint

图 11 (a)实验装置; (b)超材料板样件; (c)样件置于阻抗管内

Figure 11. (a) Experimental facility; (b) metamaterial plate sample; (c) sample positioned in impedance tube.

DownLoad: Full-Size Img PowerPoint

图 12 实验测量与数值仿真得到的传输损失对比　(a)无振子板; (b) 4振子超材料板

Figure 12. Comparison of transmission loss between experimental measurement and numerical simulation: (a) Non-oscillator plate; (b) four-oscillator metamaterial plate.

DownLoad: Full-Size Img PowerPoint

表 1 材料参数

Table 1. Material parameters.

Material $\rho $/(kg⋅m^–3) E /(10¹⁰ Pa) Possion ratio

Aluminum 2700 7 0.33
Steel 7780 21.06 0.3
Epoxy resin 1150 0.435 0.38

Plumbum 11600 40.8 0.369

DownLoad: CSV

表 2 三种声学板结构的结构参数

Table 2. Structural parameters of the three structures.

Model a/mm h/mm k₁/(N⋅m^–1) Stiffness ratio Pre-compression m/kg

QZS 25 4 10000 0.8 0.2 0.1
MSP 25 4 10000 0 0 0.1
NOP 25 4 0 0 0 0

DownLoad: CSV

表 3 准零刚度单元在正等效刚度区的调节参数

Table 3. Selected values of spring stiffness and pre-compression in the regime of positive equivalent stiffness.

Group k₁ /(N⋅m^–1) Stiffness ratio Pre-compression

Case1 10000 0.4 0.2
Case2 10000 0.6 0.2
Case3 10000 0.8 0.2
Case4
Case5 10000
10000 0.4
0.4 0.3
0.376

DownLoad: CSV

表 4 准零刚度单元在负等效刚度区的调节参数

Table 4. Selected values of spring stiffness and pre-compression in the regime of negative equivalent stiffness.

Group k₁/(N⋅m^–1) Stiffness ratio Pre-compression

Case1 10000 2.0 0.2
Case2 10000 3.0 0.2
Case3
Case4 10000
10000 0.8
0.8 0.4
0.8

DownLoad: CSV

表 5 有限大四振子超材料板的力学参数及局域共振频率

Table 5. Mechanical parameters and local resonance frequencies of finite four-oscillator metamaterial plate.

k₁/(N·m^–1) k₂/(N·m^–1) Pre-compression m/g Experiment f₀/Hz FEM f₀/ Hz

A 35137.8 11322.1 0.2 19.14 178 176
B 35137.8 1093.16 0.2 19.14 211 210
C 35137.8 11322.1 0.2 10.17 254 242
D 35137.8 11322.1 0.02 10.17 300 289

DownLoad: CSV

map

[1]	田源, 葛浩, 卢明辉, 陈延锋 2019 68 194301 Google Scholar Tian Y, Ge H, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 194301 Google Scholar
[2]	Ma G C, Sheng P 2016 Sci. Adv. 2 e1501595 Google Scholar
[3]	丁昌林, 董仪宝, 赵晓鹏 2018 67 194301 Google Scholar Ding C L, Dong Y B, Zhao X P 2018 Acta Phys. Sin. 67 194301 Google Scholar
[4]	Liu Z Y, Chan C T, Sheng P 2005 Phys. Rev. B 71 014103 Google Scholar
[5]	Fang N, Xi D J, Xu J Y, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452 Google Scholar
[6]	Deng K, Ding Y Q, He Z J, Zhao H P, Shi J, Liu Z Y 2009 J. Appl. Phys. 105 188505 Google Scholar
[7]	Zhu X F, Liang B, Kan W W, Zou X Y, Cheng J C 2011 Phys. Rev. Lett. 106 014301 Google Scholar
[8]	Peng S S, He Z J, Jia H, Zhang A Q, Qiu C Y, Ke M Z, Liu Z Y 2010 Appl. Phys. Lett. 96 263502 Google Scholar
[9]	Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Sheng P 2012 Nat. Commun. 3 756 Google Scholar
[10]	Kushwaha M S, Halevi P, Dobrzynski L, Djafari-Rouhani B 1993 Phys. Rev. Lett. 71 2022 Google Scholar
[11]	Liu Z Y, Zhang X, Mao Y, Zhu Y Y, Yang Z, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[12]	张佳龙, 姚宏, 杜军, 赵静波, 董亚科, 祁鹏山 2016 硅酸盐学报 44 1440 Google Scholar Zhang J L, Yao H, Du J, Zhao J B, Dong Y K, Qi P S 2016 J. Chin. Ceramic Soc. 44 1440 Google Scholar
[13]	张思文, 吴九汇 2013 62 134302 Google Scholar Zhang S W, Wu J H 2013 Acta Phys. Sin. 62 134302 Google Scholar
[14]	张永燕, 吴九汇, 钟宏民 2017 66 094301 Google Scholar Zhang Y Y, Wu J H, Zhong H M 2017 Acta Phys. Sin. 66 094301 Google Scholar
[15]	张若军, 肖勇, 温激鸿, 郁殿龙 2016 振动工程学报 29 905 Google Scholar Zhang R J, Xiao Y, Wen J H, Yu D L 2016 J. Vib. Eng. 29 905 Google Scholar
[16]	乔厚, 何锃, 张恒堃, 彭伟才, 江雯 2019 68 128101 Google Scholar Qiao H, He Z, Zhang H K, Peng W C, Jiang W 2019 Acta Phys. Sin. 68 128101 Google Scholar
[17]	梅军, 杨旻, 杨志宇, 陈傲轩, 沈平 2010 物理 39 243 Mei J, Yang M, Yang Z Y, Chen A X, Shen P 2010 Physics 39 243
[18]	贺子厚, 赵静波, 姚宏, 陈鑫 2019 68 214302 Google Scholar He Z H, Zhao J B, Yao H, Chen X 2019 Acta Phys. Sin. 68 214302 Google Scholar
[19]	贺子厚, 赵静波, 姚宏, 蒋娟娜, 陈鑫 2019 68 134302 Google Scholar He Z H, Zhao J B, Yao H, Jiang J N, Chen X 2019 Acta Phys. Sin. 68 134302 Google Scholar
[20]	Xiao Y, Wen J H, Wen X S 2012 J. Phys. D:Appl. Phys. 45 195401 Google Scholar
[21]	Xiao Y, Wen J H, Wen X S 2012 J. Sound Vib. 331 5408 Google Scholar
[22]	Huang X C, Liu X T, Sun J Y, Zhang Z Y, Hua H X 2014 J. Sound Vib. 333 1132 Google Scholar
[23]	Carrella A, Brennan M J, Waters T P 2007 J. Sound Vib. 301 678 Google Scholar
[24]	Zheng Y S, Zhang X N, Luo Y J, Zhang Y H, Xie S L 2018 Mech. Syst. Sig. Process. 100 135 Google Scholar
[25]	Wang K, Zhou J X, Cai C Q, Xu D L, Ouyang H J 2019 Appl. Math. Modell. 73 581 Google Scholar
[26]	张浩 2016 博士学位论文 (长沙: 国防科技大学) Zhang H 2016 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[27]	杜功焕, 朱哲民, 龚秀芬 2012 声学基础 (南京: 南京大学出版社) 第71页 Du G H, Zhu Z M, Gong X F 2012 Acoustic Basis (Nanjing: Nanjing University Press) p71 (in Chinese)
[28]	李佩 2014 博士学位论文 (北京: 北京理工大学) Li P 2014 Ph. D. Dissertation (Beijing: Beijing Institute of Technology) (in Chinese)
[29]	何琳, 朱海潮, 邱小军, 杜功焕 2006 声学理论与工程应用 (北京: 科学出版社) 第177页 He L, Zhu H C, Qiu X J, Du G H 2006 Acoustic Theory and Engineering Application (Beijing: Science Press) p177 (in Chinese)

[1]	Wei Wei, Guan Feng, Fang Xin. Integrated vibration absorption and isolation design method for metamaterial beams based on bandgap wave-insulating vibration isolatior. Acta Physica Sinica, 2024, 73(22): 224602. doi: 10.7498/aps.73.20241135
[2]	Cui Tie-Jun, Wu Hao-Tian, Liu Shuo. Research progress of information metamaterials. Acta Physica Sinica, 2020, 69(15): 158101. doi: 10.7498/aps.69.20200246
[3]	Zhai Shi-Long, Wang Yuan-Bo, Zhao Xiao-Peng. A kind of tunable acoustic metamaterial for low frequency absorption. Acta Physica Sinica, 2019, 68(3): 034301. doi: 10.7498/aps.68.20181908
[4]	Wang Fei, Huang Yi-Wang, Sun Qi-Hang. Effect of gas bubble volume fraction on low-frequency acoustic characteristic of sandy sediment. Acta Physica Sinica, 2017, 66(19): 194302. doi: 10.7498/aps.66.194302
[5]	Zhu Xi-Xi, Xiao Yong, Wen Ji-Hong, Yu Dian-Long. Flexural wave band gaps and vibration reduction properties of a locally resonant stiffened plate. Acta Physica Sinica, 2016, 65(17): 176202. doi: 10.7498/aps.65.176202
[6]	Xue Jia, Qin Ji-Liang, Zhang Yu-Chi, Li Gang, Zhang Peng-Fei, Zhang Tian-Cai, Peng Kun-Chi. Measurement of standard vacuum noise at low frequencies. Acta Physica Sinica, 2016, 65(4): 044211. doi: 10.7498/aps.65.044211
[7]	Wu Jian, Bai Xiao-Chun, Xiao Yong, Geng Ming-Xin, Yu Dian-Long, Wen Ji-Hong. Low frequency band gaps and vibration reduction properties of a multi-frequency locally resonant phononic plate. Acta Physica Sinica, 2016, 65(6): 064602. doi: 10.7498/aps.65.064602
[8]	Zhou Zhuo-Hui, Liu Xiao-Lai, Huang Da-Qing, Kang Fei-Yu. Design and preparation of a low frequency absorber based on hollowed-out cross-shaped meta-material structure. Acta Physica Sinica, 2014, 63(18): 184101. doi: 10.7498/aps.63.184101
[9]	Hou Li-Na, Hou Zhi-Lin, Fu Xiu-Jun. Defect state of the locally resonant phononic crystal. Acta Physica Sinica, 2014, 63(3): 034305. doi: 10.7498/aps.63.034305
[10]	Cheng Cong, Wu Fu-Gen, Zhang Xin, Yao Yuan-Wei. Phononic crystal multi-channel low-frequency filter based on locally resonant unit. Acta Physica Sinica, 2014, 63(2): 024301. doi: 10.7498/aps.63.024301
[11]	Lu Lei, Qu Shao-Bo, Shi Hong-Yu, Zhang An-Xue, Zhang Jie-Que, Ma Hua. A miniaturized low-frequency polarization-insensitive metamaterial absorber based on broadside-coupled spiral structures. Acta Physica Sinica, 2013, 62(15): 158102. doi: 10.7498/aps.62.158102
[12]	Wang Ying, Cheng Yong-Zhi, Nie Yan, Gong Rong-Zhou. Design and experiments of low-frequency broadband metamaterial absorber based on lumped elements. Acta Physica Sinica, 2013, 62(7): 074101. doi: 10.7498/aps.62.074101
[13]	Zhang Si-Wen, Wu Jiu-Hui. Low-frequency band gaps in phononic crystals with composite locally resonant structures. Acta Physica Sinica, 2013, 62(13): 134302. doi: 10.7498/aps.62.134302
[14]	Shen Xiao-Peng, Cui Tie-Jun, Ye Jian-Xiang. Dual band metamaterial absorber in microwave regime. Acta Physica Sinica, 2012, 61(5): 058101. doi: 10.7498/aps.61.058101
[15]	Liu Min, Hou Zhi-Lin, Fu Xiu-Jun. Local resonant acoustic band gaps in two-dimensional square-arranged Helmholtz resonators array. Acta Physica Sinica, 2012, 61(10): 104302. doi: 10.7498/aps.61.104302
[16]	Wen Qi-Hua, Zuo Shu-Guang, Wei Huan. Locally resonant elastic wave band gaps in flexural vibration of multi-oscillators beam. Acta Physica Sinica, 2012, 61(3): 034301. doi: 10.7498/aps.61.034301
[17]	Su Yan-Yan, Gong Bo-Yi, Zhao Xiao-Peng. Zero-index metamaterial based on double-negative structure. Acta Physica Sinica, 2012, 61(8): 084102. doi: 10.7498/aps.61.084102
[18]	Chen Sheng-Bing, Han Xiao-Yun, Yu Dian-Long, Wen Ji-Hong. Influences of different types of piezoelectric shunting circuits on band gaps of phononic beam. Acta Physica Sinica, 2010, 59(1): 387-392. doi: 10.7498/aps.59.387
[19]	Li Xiao-Chun, Liang Hong-Yu, Yi Xiu-Ying, Xiao Qing-Wu, Zhao Bao-Xing. The study of two-dimensional composite materials with wide band gap. Acta Physica Sinica, 2007, 56(5): 2784-2789. doi: 10.7498/aps.56.2784
[20]	Hua Jia, Zhang Shu, Cheng Jian-Chun. Mechanism of broad acoustic band-gap in the three-component composite. Acta Physica Sinica, 2005, 54(3): 1261-1266. doi: 10.7498/aps.54.1261

Catalog

Vol. 70, Issue 24 - 2021-12-20

Metrics

Abstract views: 7680
PDF Downloads: 295
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板