-
Head-on collisions of plasma jets are common hydrodynamic phenomena in astrophysical and laser-plasma interaction processes. Deriving scaling relationships between colliding plasmas and initial conditions of plasma jets is of great significance in optimizing the design and the data analysis of the relevant experiments. Double-cone ignition (DCI) scheme is an excellent platform for studying plasma jets’ collision, since the collision between high-speed, high-density plasma jets can be easily generated and characterized in both simulations and experiments. In this work, we employ the upgraded two-dimensional arbitrary Eulerian-Lagrange (ALE) program MULTI-2D to simulate the collision process of plasma jets with high speed (≥100 km/s) and high density (≥10 g/cm3). Using the database obtained from the simulations, hydrodynamic scaling laws describing the collision process of plasma jets are derived by the Bayesian inference method in machine learning. The Bayesian inference method not only has the parameter estimation function of traditional least square method, but also possesses other potential advantages such as giving the probability distribution of estimated parameters. Numerical results show that the collision of plasma jets with open boundaries is easy to form an isochoric plasma distribution with high-density. Increasing the initial density and velocity of the plasma jet is helpful in enhancing the density and temperature of the colliding plasma. Increasing the initial temperature of plasma jet is beneficial to achieving colliding plasmas with a higher temperature, while leading plasma density and pressure to decrease after head-on collision. When the initial density, temperature and velocity of the plasma jets are set to be 15 g/cm3, 30 eV and 300 km/s, respectively, the colliding plasma density can reach more than 300 g/cm3. This is very favorable for the following fast electron heating process in the double-cone ignition (DCI) scheme. The issue about quantum degeneracy after collision is discussed in this work. Under the typical initial conditions of plasma jets in DCI scheme ( $100\,\,\rm{km}/\mathrm{s}\leqslant {V}_{0}\leqslant 500\,\,\rm{km}/\mathrm{s},10\,\,\rm{eV}\leqslant {T}_{0}\leqslant 100\,\,\rm{eV},10\,\,\mathrm{g}/\mathrm{c}\mathrm{m}^3\leqslant {\rho }_{0}\leqslant 50\,\,\mathrm{g}/\mathrm{c}\mathrm{m}^3)$ , both quantum degenerate plasma and classical non-degenerate plasma can be obtained in a temperature range between$ 0.3{T}_{F} $ (Fermi temperature) and$ 3{T}_{F} $ . By comparing the plasma temperature with the Fermi temperature of the collision, the criterion for achieving quantum degenerate plasma or non-degenerate plasma under given initial conditions is obtained with the help of the derived hydrodynamic scaling laws. The criterion shows that higher initial velocity, higher temperature and lower density of plasma jets are required if we want to obtain non-degenerate plasma after collision.-
Keywords:
- plasma jets /
- machine learning /
- scaling laws /
- double-cone ignition
[1] Albertazzi B, Ciardi A, Nakatsutsumi M, Vinci T, Béard J, Bonito R, Billette J, Borghesi M, Burkley Z, Chen S 2014 Science 346 325
Google Scholar
[2] Li C, Ryutov D, Hu S, Rosenberg M, Zylstra A, Séguin F, Frenje J, Casey D, Johnson M G, Manuel M-E 2013 Phys. Rev. Lett. 111 235003
Google Scholar
[3] Yin C L, Li Y T, Lu X, Yuan D W, Zhong J Y, Yuan X H, Wei H G, Zhang K, Fang Y, Liao G Q, Su L N, Han B, Wang F L, Liang G Y, Yang S, Zhu J Q, Zhao G, Zhang J 2015 High Power Laser Part. Beams 27 032035
Google Scholar
[4] 裴晓星, 仲佳勇, 张凯, 郑无敌, 梁贵云, 王菲鹿, 李玉同, 赵刚 2014 14 145201
Google Scholar
Pei X X, Zhong J Y, Zhang K, Zheng W D, Liang G Y, Wang F L, Li Y T, Zhao G 2014 Acta Phys. Sin. 14 145201
Google Scholar
[5] Ke Y, Yang X, Ma Y, Xu B, Ge Z, Gan L, Meng L, Wang S, Kawata S 2018 Phys. Plasmas 25 042706
Google Scholar
[6] Lebedev S, Chittenden J, Beg F, Bland S, Ciardi A, Ampleford D, Hughes S, Haines M, Frank A, Blackman E 2002 Astrophys. J. 564 113
Google Scholar
[7] Zylstra A, Hurricane O, Callahan D, Kritcher A, Ralph J, Robey H, Ross J, Young C, Baker K, Casey D 2022 Nature 601 542
Google Scholar
[8] Lan K, Dong Y, Wu J, Li Z, Chen Y, Cao H, Hao L, Li S, Ren G, Jiang W 2021 Phys. Rev. Lett. 127 245001
Google Scholar
[9] Tabak M, Clark D, Hatchett S, Key M, Lasinski B, Snavely R, Wilks S, Town R, Stephens R, Campbell E 2005 Phys. Plasmas 12 057305
Google Scholar
[10] Murakami M, Nagatomo H, Johzaki T, Sakaiya T, Velikovich A, Karasik M, Gus' Kov S, Zmitrenko N 2014 Nucl. Fusion 54 054007
Google Scholar
[11] Hurricane O, Casey D, Landen O, Kritcher A, Nora R, Patel P, Gaffney J, Humbird K, Field J, Kruse M 2020 Phys. Plasmas 27 062704
Google Scholar
[12] Nuckolls J, Wood L, Thiessen A, Zimmerman G 1972 Nature 239 139
Google Scholar
[13] Zhang J, Wang W, Yang X, Wu D, Ma Y, Jiao J, Zhang Z, Wu F, Yuan X, Li Y 2020 Philos. T. R. Soc. A 378 20200015
Google Scholar
[14] 方可, 张喆, 李玉同, 张杰 2022 71 035204
Google Scholar
Fang K, Zhang Z, Li Y T, Zhang J 2022 Acta Phys. Sin. 71 035204
Google Scholar
[15] Wu F, Yang X, Ma Y, Zhang Q, Zhang Z, Yuan X, Liu H, Liu Z, Zhong J, Zheng J 2022 High Power Laser Sci. Eng. 10 e10
Google Scholar
[16] Ramis R, Meyer-ter-Vehn J 2016 Comput. Phys. Commun. 203 226
Google Scholar
[17] Ramis R, Meyer-ter-Vehn J, Ramírez J 2009 Comput. Phys. Commun. 180 977
Google Scholar
[18] Wu F, Ramis R, Li Z 2018 J. Comput. Phys. 357 206
Google Scholar
[19] Ramis R, Canaud B, Temporal M, Garbett W J, Philippe F 2019 Matter Radiat. Extremes 4 055402
Google Scholar
[20] 余波, 丁永坤, 蒋炜, 黄天晅, 陈伯伦, 蒲昱东, 晏骥, 陈忠靖, 张兴, 杨家敏 2017 66 235201
Google Scholar
Yu B, Ding Y K, Jiang W, Huang T X, Chen B L, Pu Y D, Yan J, Chen Z J, Zhang X, Yang J M 2017 Acta Phys. Sin. 66 235201
Google Scholar
[21] 陈忠旺, 宁成 2017 66 125202
Google Scholar
Chen Z W, Ning C, 2017 Acta Phys. Sin. 66 125202
Google Scholar
[22] Wu F, Chu Y, Ramis R, Li Z, Ma Y, Yang J, Wang Z, Ye F, Huang Z, Qi J 2018 Matter Radiat. Extremes 3 248
Google Scholar
[23] Chen S J, Ma Y Y, Wu F Y, Yang X H, Yuan Y, Cui Y, Ramis R 2021 Chin. Phys. B 30 115201
Google Scholar
[24] Ramis R, Meyer-Ter-Vehn J 2014 Laser Part. Beams 32 41
Google Scholar
[25] Kemp A, Meyer-ter-Vehn J 1998 Nucl. Instrum. Meth. A 415 674
Google Scholar
[26] Eidmann K 1994 Laser Part. Beams 12 223
Google Scholar
[27] More R, Warren K, Young D, Zimmerman G 1988 Phys. Fluids 31 3059
Google Scholar
[28] Von Neumann J, Richtmyer R D 1950 J. Appl. Phys. 21 232
Google Scholar
[29] Noh W F 1987 J. Comput. Phys. 72 78
Google Scholar
[30] 王瑞利, 林忠, 魏兰, 葛全文 2007 计算物理 24 407
Google Scholar
Wang R L, Lin Z, Wei L, Ge Q W, 2007 Chin. J. Comput. Phys. 24 407
Google Scholar
[31] Atzeni S, Meyer-ter-Vehn J 2004 The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter (Oxford: Oxford University Press), pp38, 330
[32] Chabrier G, Douchin F, Potekhin A 2002 J. Phys. Condens. Mat. 14 9133
Google Scholar
[33] Haas F 2005 Phys. Plasmas 12 062117
Google Scholar
[34] Salvatier J, Wiecki T V, Fonnesbeck C 2016 PeerJ Comput. Sci. 2 e55
Google Scholar
[35] Gopalaswamy V, Betti R, Knauer J, Luciani N, Patel D, Woo K, Bose A, Igumenshchev I, Campbell E, Anderson K 2019 Nature 565 581
Google Scholar
-
图 1 不同时刻锥形等离子体喷流对撞的密度和温度分布图
Figure 1. Density and temperature distributions of conical plasma jets at different times during the collision.
图 2 锥形喷流对撞过程中的等离子体状态在温度-密度相图上的运动轨迹, 箭头表示时间的增大方向, 橙色直线表示不同密度对应的费米温度
Figure 2. The trajectory of the plasma jet on the temperature-density phase diagram during the collision, the arrow in the Fig. indicates the increasing direction of time, and the orange line indicates the Fermi temperature at different densities.
图 3 对撞过程中快点火方向面密度、峰值压强和对撞区归一化X射线辐射功率随时间变化曲线
Figure 3. Time evolution of areal density, peak pressure in fast ignition direction and normalized X-ray radiation emission power in collision area.
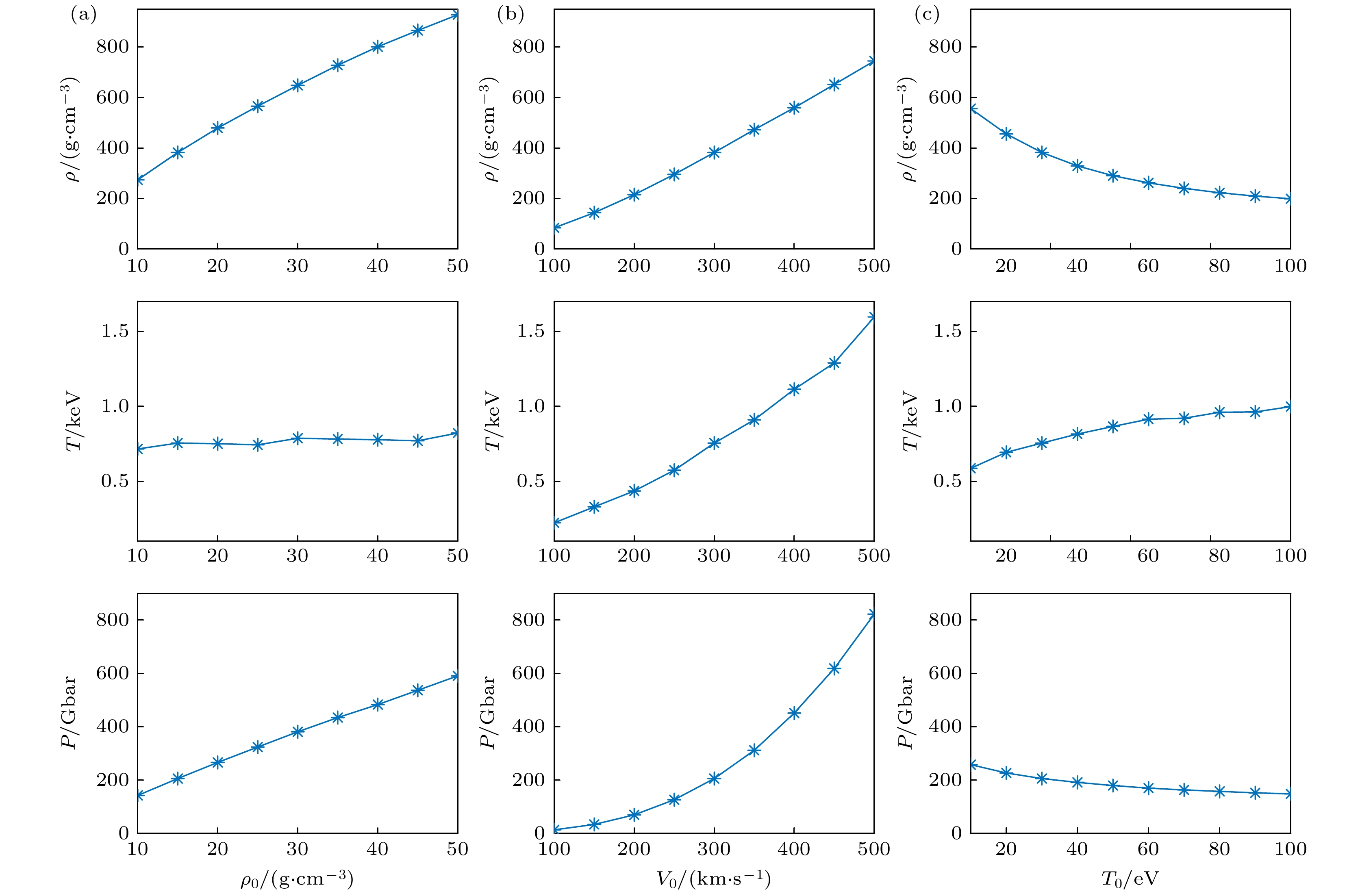
图 4 对撞等离子体参数随喷流初始条件的变化曲线 (a) V0 = 300 km/s, T0 = 30 keV; (b) ρ0 = 15 g/cm3, T0 = 30 keV; (c) ρ0 = 15 g/cm3, V0 = 300 km/s
Figure 4. Variations of colliding plasma parameters with the initial conditions of plasma jets: (a) V0 = 300 km/s, T0 = 30 keV; (b) ρ0 = 15 g/cm3, T0 = 30 keV; (c) ρ0 = 15 g/cm3, V0 = 300 km/s.
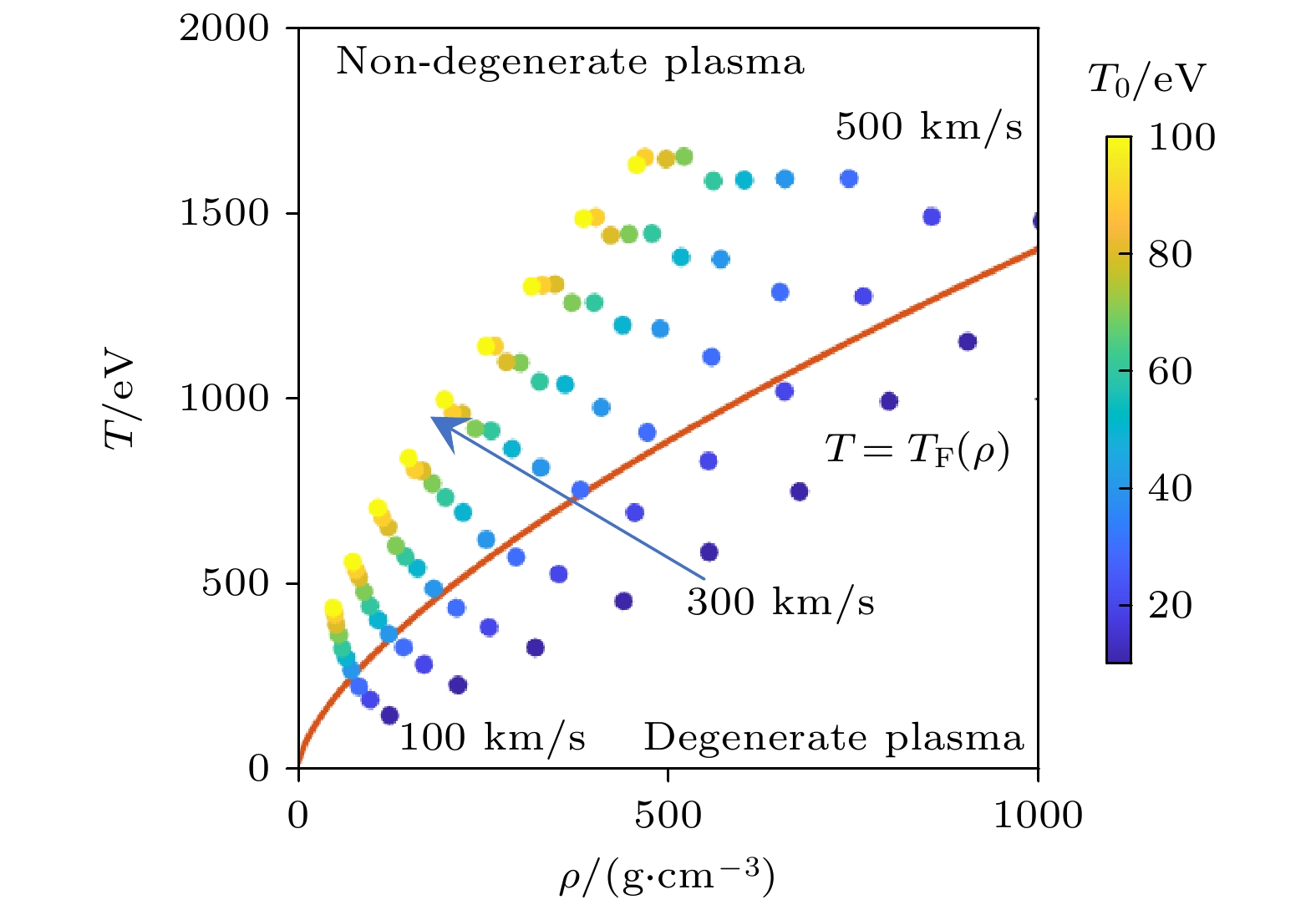
图 5 喷流初始密度为15 g/cm3时, 不同初始温度和初始速度获得的对撞等离子体状态, 橙线表示费米温度随密度的变化曲线, 箭头表示喷流初始速度相同时, 喷流初始温度的增大方向
Figure 5. Colliding plasma states obtained at different initial temperatures and velocities when the initial jet density is 15 g/cm3, the orange line in the figure represents the variation curve of Fermi temperature with density, and the arrow represents the increasing direction of the initial temperature when the initial velocity is the same.
图 6 (a) 贝叶斯推断得到的对撞密度定标关系, 橙色直线表示拟合数据和模拟数据完全一致时的参考线; (b) 相关参数的归一化概率分布灰色直线表示每个参数归一化概率分布对应的平均值位置
Figure 6. (a) The calibration relationship of plasma density, the orange line represents the reference line when the fitting data is completely consistent with the simulation data; (b) the normalized probability distribution of relevant parameters inferred by Bayes, the gray line represents the average position corresponding to the normalized probability distribution of each parameter.
图 7 对撞后的氘氚等离子体状态在压强-温度相图的分布
Figure 7. The DT plasma states after collision in pressure-temperature phase diagram.
表 1 对撞等离子体参数和喷流初始条件的流体力学定标关系
Table 1. Scaling laws between colliding plasma parameters and the initial conditions of plasma jets.
对撞等离子体参数 对撞等离子体参数和喷流初始
参数的流体定标关系ρ/(g·cm–3) $ \rho {\text{ = }}0.074\rho _0^{0.74}V_0^{1.33}T_0^{ - 0.32} $ ρR/(g·cm–2) $ \rho R{\text{ = }}0.002\rho _0^{0.85}V_0^{0.91}T_0^{ - 0.24} $ T/eV $ T{\text{ = }}0.437\rho _0^{0.12}V_0^{1.16}T_0^{0.17} $ P/Mbar $ P{\text{ = }}0.020\rho _0^{0.86}V_0^{2.56}T_0^{ - 0.21} $ 
DownLoad: CSV
-
[1] Albertazzi B, Ciardi A, Nakatsutsumi M, Vinci T, Béard J, Bonito R, Billette J, Borghesi M, Burkley Z, Chen S 2014 Science 346 325
Google Scholar
[2] Li C, Ryutov D, Hu S, Rosenberg M, Zylstra A, Séguin F, Frenje J, Casey D, Johnson M G, Manuel M-E 2013 Phys. Rev. Lett. 111 235003
Google Scholar
[3] Yin C L, Li Y T, Lu X, Yuan D W, Zhong J Y, Yuan X H, Wei H G, Zhang K, Fang Y, Liao G Q, Su L N, Han B, Wang F L, Liang G Y, Yang S, Zhu J Q, Zhao G, Zhang J 2015 High Power Laser Part. Beams 27 032035
Google Scholar
[4] 裴晓星, 仲佳勇, 张凯, 郑无敌, 梁贵云, 王菲鹿, 李玉同, 赵刚 2014 14 145201
Google Scholar
Pei X X, Zhong J Y, Zhang K, Zheng W D, Liang G Y, Wang F L, Li Y T, Zhao G 2014 Acta Phys. Sin. 14 145201
Google Scholar
[5] Ke Y, Yang X, Ma Y, Xu B, Ge Z, Gan L, Meng L, Wang S, Kawata S 2018 Phys. Plasmas 25 042706
Google Scholar
[6] Lebedev S, Chittenden J, Beg F, Bland S, Ciardi A, Ampleford D, Hughes S, Haines M, Frank A, Blackman E 2002 Astrophys. J. 564 113
Google Scholar
[7] Zylstra A, Hurricane O, Callahan D, Kritcher A, Ralph J, Robey H, Ross J, Young C, Baker K, Casey D 2022 Nature 601 542
Google Scholar
[8] Lan K, Dong Y, Wu J, Li Z, Chen Y, Cao H, Hao L, Li S, Ren G, Jiang W 2021 Phys. Rev. Lett. 127 245001
Google Scholar
[9] Tabak M, Clark D, Hatchett S, Key M, Lasinski B, Snavely R, Wilks S, Town R, Stephens R, Campbell E 2005 Phys. Plasmas 12 057305
Google Scholar
[10] Murakami M, Nagatomo H, Johzaki T, Sakaiya T, Velikovich A, Karasik M, Gus' Kov S, Zmitrenko N 2014 Nucl. Fusion 54 054007
Google Scholar
[11] Hurricane O, Casey D, Landen O, Kritcher A, Nora R, Patel P, Gaffney J, Humbird K, Field J, Kruse M 2020 Phys. Plasmas 27 062704
Google Scholar
[12] Nuckolls J, Wood L, Thiessen A, Zimmerman G 1972 Nature 239 139
Google Scholar
[13] Zhang J, Wang W, Yang X, Wu D, Ma Y, Jiao J, Zhang Z, Wu F, Yuan X, Li Y 2020 Philos. T. R. Soc. A 378 20200015
Google Scholar
[14] 方可, 张喆, 李玉同, 张杰 2022 71 035204
Google Scholar
Fang K, Zhang Z, Li Y T, Zhang J 2022 Acta Phys. Sin. 71 035204
Google Scholar
[15] Wu F, Yang X, Ma Y, Zhang Q, Zhang Z, Yuan X, Liu H, Liu Z, Zhong J, Zheng J 2022 High Power Laser Sci. Eng. 10 e10
Google Scholar
[16] Ramis R, Meyer-ter-Vehn J 2016 Comput. Phys. Commun. 203 226
Google Scholar
[17] Ramis R, Meyer-ter-Vehn J, Ramírez J 2009 Comput. Phys. Commun. 180 977
Google Scholar
[18] Wu F, Ramis R, Li Z 2018 J. Comput. Phys. 357 206
Google Scholar
[19] Ramis R, Canaud B, Temporal M, Garbett W J, Philippe F 2019 Matter Radiat. Extremes 4 055402
Google Scholar
[20] 余波, 丁永坤, 蒋炜, 黄天晅, 陈伯伦, 蒲昱东, 晏骥, 陈忠靖, 张兴, 杨家敏 2017 66 235201
Google Scholar
Yu B, Ding Y K, Jiang W, Huang T X, Chen B L, Pu Y D, Yan J, Chen Z J, Zhang X, Yang J M 2017 Acta Phys. Sin. 66 235201
Google Scholar
[21] 陈忠旺, 宁成 2017 66 125202
Google Scholar
Chen Z W, Ning C, 2017 Acta Phys. Sin. 66 125202
Google Scholar
[22] Wu F, Chu Y, Ramis R, Li Z, Ma Y, Yang J, Wang Z, Ye F, Huang Z, Qi J 2018 Matter Radiat. Extremes 3 248
Google Scholar
[23] Chen S J, Ma Y Y, Wu F Y, Yang X H, Yuan Y, Cui Y, Ramis R 2021 Chin. Phys. B 30 115201
Google Scholar
[24] Ramis R, Meyer-Ter-Vehn J 2014 Laser Part. Beams 32 41
Google Scholar
[25] Kemp A, Meyer-ter-Vehn J 1998 Nucl. Instrum. Meth. A 415 674
Google Scholar
[26] Eidmann K 1994 Laser Part. Beams 12 223
Google Scholar
[27] More R, Warren K, Young D, Zimmerman G 1988 Phys. Fluids 31 3059
Google Scholar
[28] Von Neumann J, Richtmyer R D 1950 J. Appl. Phys. 21 232
Google Scholar
[29] Noh W F 1987 J. Comput. Phys. 72 78
Google Scholar
[30] 王瑞利, 林忠, 魏兰, 葛全文 2007 计算物理 24 407
Google Scholar
Wang R L, Lin Z, Wei L, Ge Q W, 2007 Chin. J. Comput. Phys. 24 407
Google Scholar
[31] Atzeni S, Meyer-ter-Vehn J 2004 The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter (Oxford: Oxford University Press), pp38, 330
[32] Chabrier G, Douchin F, Potekhin A 2002 J. Phys. Condens. Mat. 14 9133
Google Scholar
[33] Haas F 2005 Phys. Plasmas 12 062117
Google Scholar
[34] Salvatier J, Wiecki T V, Fonnesbeck C 2016 PeerJ Comput. Sci. 2 e55
Google Scholar
[35] Gopalaswamy V, Betti R, Knauer J, Luciani N, Patel D, Woo K, Bose A, Igumenshchev I, Campbell E, Anderson K 2019 Nature 565 581
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5735
- PDF Downloads: 180
- Cited By: 0
