-
The Chinese First Quasi-axisymmetric Stellarator (CFQS) is now the only quasi-axisymmetric stellarator under construction in the world. In this work, ion temperature gradient (ITG) mode in CFQS is studied by using gyrokinetic Vlasov code GKV. The basic characteristics of the eletrtostatic ITG are separately given under the adiabatic condition and the non-adiabatic condition. There is a critical temperature gradient for ITG. The growth rate of ITG is proportional to the temperature gradient. Furthermore, the growth rate depends on not only the absolute value of density gradient, but also the plus or minus sign of the density gradient. The negative density gradient can strongly suppress the ITG. The kinetic electron can destabilize the ITG and the electron temperature gradient can also destabilize the ITG. For electromagnetic condition, the ITG modes can be suppressed by the finite plasma beta, and then a transition from ITG to Alfvenic ion temperature gradient mode/kinetic ballooning mode (AITG/KBM) comes into being. The maximum growth rate of KBM is linearly proportional to density gradient and temperature gradient when both gradients are large.
-
Keywords:
- Chinese First Quasi-axisymmetric Stellarator /
- ion temperature gradient mode /
- plasma beta /
- kinetic ballooning mode
[1] Xu Y 2016 Matter Radiat. Extremes 1 192
Google Scholar
[2] Ho D D M 1987 Phys. Fluids 30 442
Google Scholar
[3] Boozer A H 1995 Plasma Phys. Controlled Fusion 37 A103
Google Scholar
[4] Subbotin A A, Mikhailov M I, Shafranov V D, Isaev M Yu, Nührenberg C, Nührenberg J, Zille R, Nemov V V, Kasilov SV, Kalyuzhnyj V N 2006 Nucl. Fusion 46 921
Google Scholar
[5] Garabedian P 1996 Phys. Plasmas 3 2483
Google Scholar
[6] Shimizu A, Liu H F, Isobe M, Okamura S, Nishimura S, Suzuki C, Xu Y, Zhang X, Liu B, Huang J, Wang X Q, Liu H, Tang C J, CFQS team 2018 Plasma Fusion Res. 13 3403123
Google Scholar
[7] Zarnstorff M C, Berry L A, Brooks A, Fredrickson1 E, Fu G Y, Hirshman S, Hudson, Ku L P, Lazarus E, Mikkelsen D, Monticello D, Neilson G H, Pomphrey N, Reiman A, Spong D, Strickler D, Boozer A, Cooper W A, Goldston R, Hatcher R, Isaev M, Kessel C, Ewandowski J L, Lyon J F, Merkel P, Mynick H, Nelson B E, Nuehrenberg C, Redi M, Reiersen W, Rutherford P, Sanchez R, Schmidt J, White R B 2001 Plasma Phys. Controlled Fusion 43 A237
Google Scholar
[8] Okamura S, Matsuoka K, Nishimura S, Isobe M, Nomura I, Suzuki C, Shimizu A, Murakami S, Nakajima N, Yokoyama M 2001 Nucl. Fusion 41 1865
Google Scholar
[9] Liu H F, Shimizu A, Isobe M, Okamura S, Nishimura S, Suzuki C, Xu Y, Zhang X, Liu B, Huang J, Wang X Q, Liu H, Tang C J, Yin D P, Wan Y, CFQS team 2018 Plasma Fusion Res. 13 3405067
Google Scholar
[10] Isobe M, Shimizu A, Liu H F, Liu H, Xiong G Z, Yin D P, Ogawa K, Yoshimura Y, Nakata M, Kinoshita S, Okamura S, tang C J, Xu Y, CFQS Team 2019 Plasma Fusion Res. 14 3402074
Google Scholar
[11] Liu H F, Shimizu A, Xu Y, Okamura S, Kinoshita S, Isobe M, Li Y B, Xiong G Z, Wang X Q, Huang J, Cheng J, Liu H, Zhang X, Yin D P, Wang Y, Murase T, Nakagawa S, Tang C J 2021 Nucl. Fusion 61 016014
Google Scholar
[12] Wang X Q, Xu Y, Shimizu A, Isobe M, Okamura S, Todo Y, Wang H, Liu H F, Huang J, Zhang X, Liu H, Cheng J, Tang C J, CFQS team 2021 Nucl. Fusion 61 036021
Google Scholar
[13] Horton W 1999 Rev. Mod. Phys. 71 735
Google Scholar
[14] Watanabe T H, Sugama H 2006 Nucl. Fusion 46 24
Google Scholar
[15] Nakata M, Nunami M, Sugama H 2017 Phys. Rev. Lett. 118 165002
Google Scholar
[16] Antonsen T M, Lane B 1980 Phys. Fluids 23 1205
Google Scholar
[17] Nakata M, Honda M, Yoshida M, Urano H, Nunami M, Maeyama S, Watanabe T H, Sugama H 2016 Nucl. Fusion 56 086010
Google Scholar
[18] Beer M A, Cowley S C, Hammett G W 1995 Phys. Plasmas 2 2687
Google Scholar
[19] Romanelli M, Bourdelle C, Dorland W 2004 Phys. Plasmas 11 3845
Google Scholar
[20] Du H R, Jhang H, Hahm T S, Dong J Q, Wang Z X 2017 Phys. Plasmas 24 122501
Google Scholar
[21] 沈勇, 董家齐, 徐红兵 2018 67 195203
Google Scholar
Shen Y, Dong J Q, Xu H B 2018 Acta Phys. Sin. 67 195203
Google Scholar
[22] Baumgaertel J A, Hammett G W, Mikkelsen D R, Nunami M, Xanthopoulos P 2012 Phys. Plasmas 19 122306
Google Scholar
[23] Dominguez R R, Waltz R E 1988 Phys. Fluids 31 3147
Google Scholar
[24] Nunami M, Watanabe T H, Sugama H, Tanaka K 2011 Plasma Fusion Res. 6 1403001
Google Scholar
[25] Alcusón J A, Xanthopoulos P, Plunk G G, Helander P, Wilms F, Turkin Y, Stechow A von, Grulke O 2020 Plasma Phys. Controlled Fusion 62 035005
Google Scholar
[26] 罗一鸣, 王占辉, 陈佳乐, 吴雪科, 付彩龙, 何小雪, 刘亮, 杨曾辰, 李永高, 高金明, 杜华荣, 昆仑集成模拟设计组 2022 71 075201
Google Scholar
Luo Y M, Wang Z H, Chen J L, Wu X K, Fu C L, He X X, Liu L, Yang Z C, Li Y G, Gao J M, Du H R, Kulun Integrated Simulation and Design Group 2022 Acta Phys. Sin. 71 075201
Google Scholar
[27] Mahmood M A, Rafiq T, Persson M, Weiland J 2009 Phys. Plasmas 16 022503
Google Scholar
[28] Dong J Q, Mahajan S M, Horton W 1997 Phys. Plasmas 4 755
Google Scholar
[29] Peeters A G, Angioni C, Apostoliceanu M, Jenko F, Ryter F, the ASDEX Upgrade team 2005 Phys. Plasmas 12 022505
Google Scholar
[30] Sandberg I, Isliker H, Pavlenko V P 2007 Phys. Plasmas 14 092504
Google Scholar
[31] Qi L, Kwon J, Hahm T S, Jo G 2016 Phys. Plasmas 23 062513
Google Scholar
[32] Malinov P, Zonca F 2005 J. Plasma Phys. 71 301
Google Scholar
[33] Kim J Y, Han H S 2017 Phys. Plasmas 24 072501
Google Scholar
[34] Pueschel M J, Jenko F 2010 Phys. Plasmas 17 062307
Google Scholar
[35] Xie H S, Lu Z X, Li B 2018 Phys. Plasmas 25 072106
Google Scholar
[36] Aleynikova K, Zocco A 2017 Phys. Plasmas 24 092106
Google Scholar
[37] Turnbull A D, Strait E J, Heidbrink W W, Chu M S, Duong H H, Greene J M, Lao L L, Taylor T S, Thompson S J 1993 Phys. Fluids B 5 2546
Google Scholar
[38] Dong J, Chen L, Zonca F 1999 Nucl. Fusion 39 1041
Google Scholar
[39] 谢华生 2015 博士学位论文 (杭州: 浙江大学)
Xie H S 2015 Ph. D. Dissertation (Hangzhou: Zhejiang University) (in Chinese)
[40] Aleynikova K, Zocco1 A, Xanthopoulos1 P, Helander1 P, Nührenberg C 2018 J. Plasma Phys. 84 745840602
Google Scholar
-
图 1 不同密度梯度和温度梯度下绝热ITG的增长率波数谱 (a)
$ {R}_{0}/{L}_{n}=-2 $ ; (b)$ {R}_{0}/{L}_{n}=2 $ ; (c)$ {R}_{0}/{L}_{n}=8 $ Figure 1. Growth rate spectra of ITG for different density gradients and temperature gradients: (a)
$ {R}_{0}/{L}_{n}=-2 $ ; (b)$ {R}_{0}/{L}_{n}=2 $ ; (c)$ {R}_{0}/{L}_{n}=8 $ .
图 2 不同密度梯度和温度梯度下绝热ITG的频率波数谱 (a)
$ {R}_{0}/{L}_{n}=-2 $ ; (b)$ {R}_{0}/{L}_{n}=2 $ ; (c)$ {R}_{0}/{L}_{n}=8 $ Figure 2. Real frequency spectra of ITG for different density gradients and temperature gradients: (a)
$ {R}_{0}/{L}_{n}=-2 $ ; (b)$ {R}_{0}/{L}_{n}=2 $ ; (c)$ {R}_{0}/{L}_{n}=8 $ .
图 3 绝热ITG的最大增长率与密度梯度和温度梯度的关系
Figure 3. Relationship of the maximum growth rate of adiabatic ITG to
$ {R}_{0}/{L}_{n} $ and$ {R}_{0}/{L}_{T} $ .
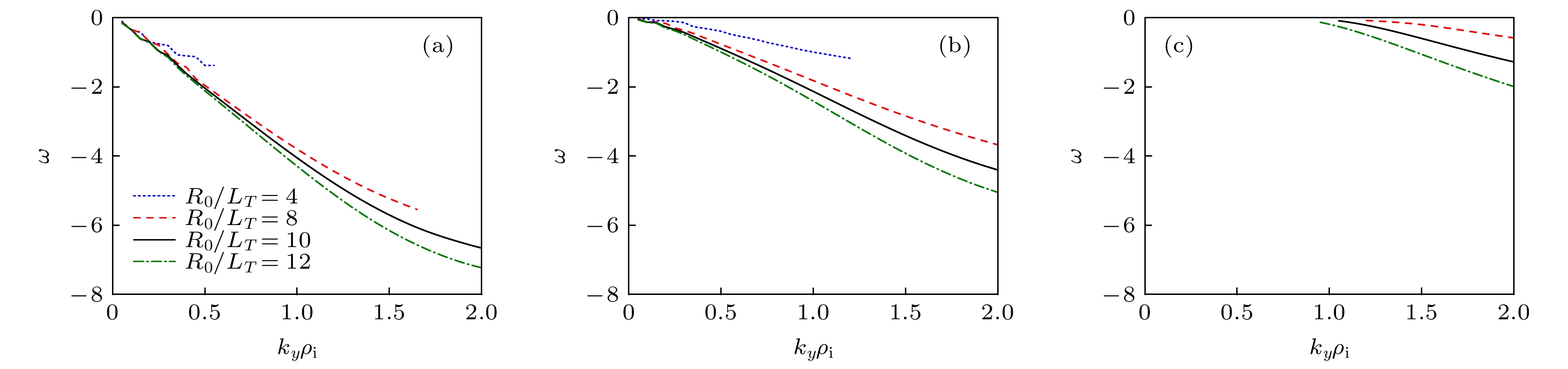
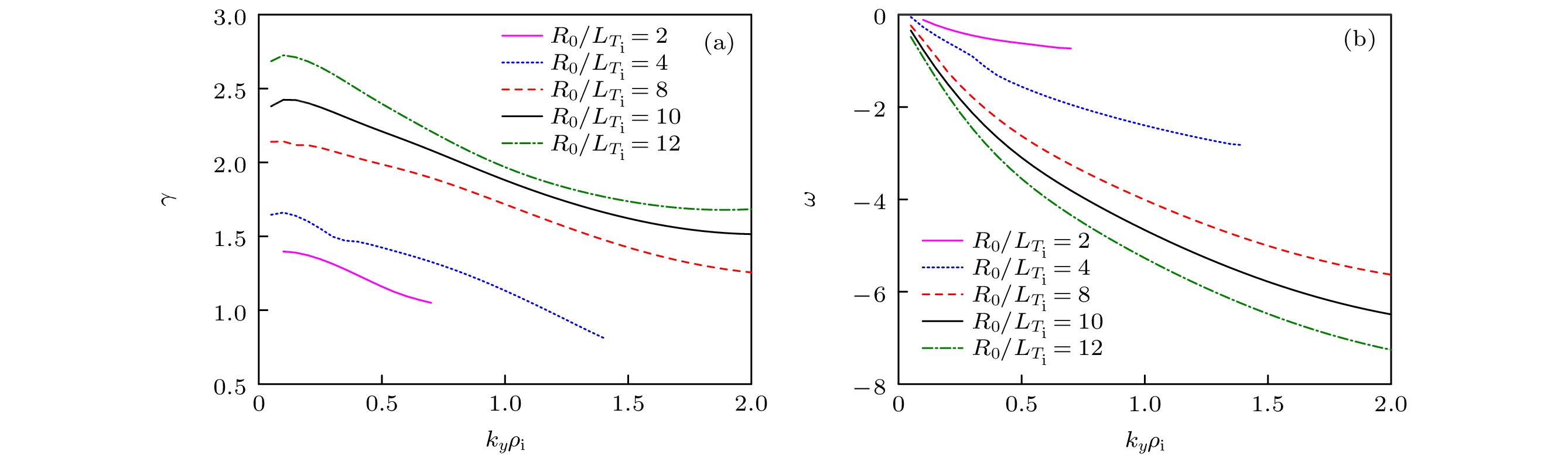
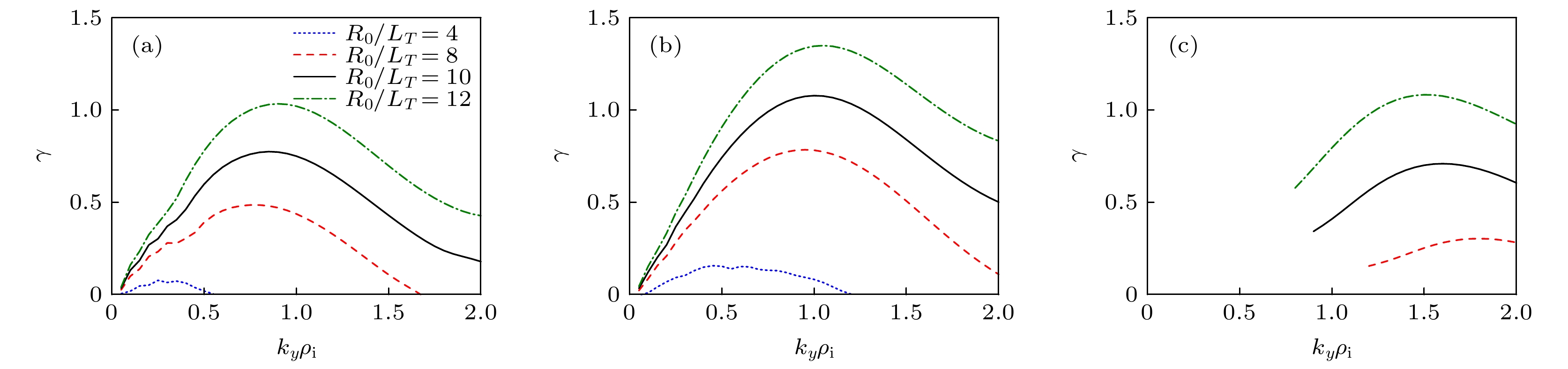
图 4 考虑捕获电子效应后ITG的增长率(a)和频率(b)波数谱, 其中
$ {R}_{0}/{L}_{n}=2 $ , 电子温度梯度标长和离子温度梯度标长相等, 即$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}={R}_{0}/{L}_{{T}_{\mathrm{i}}} $ Figure 4. Growth rate (a) and real frequency spectra (b) of kinetic ITG for
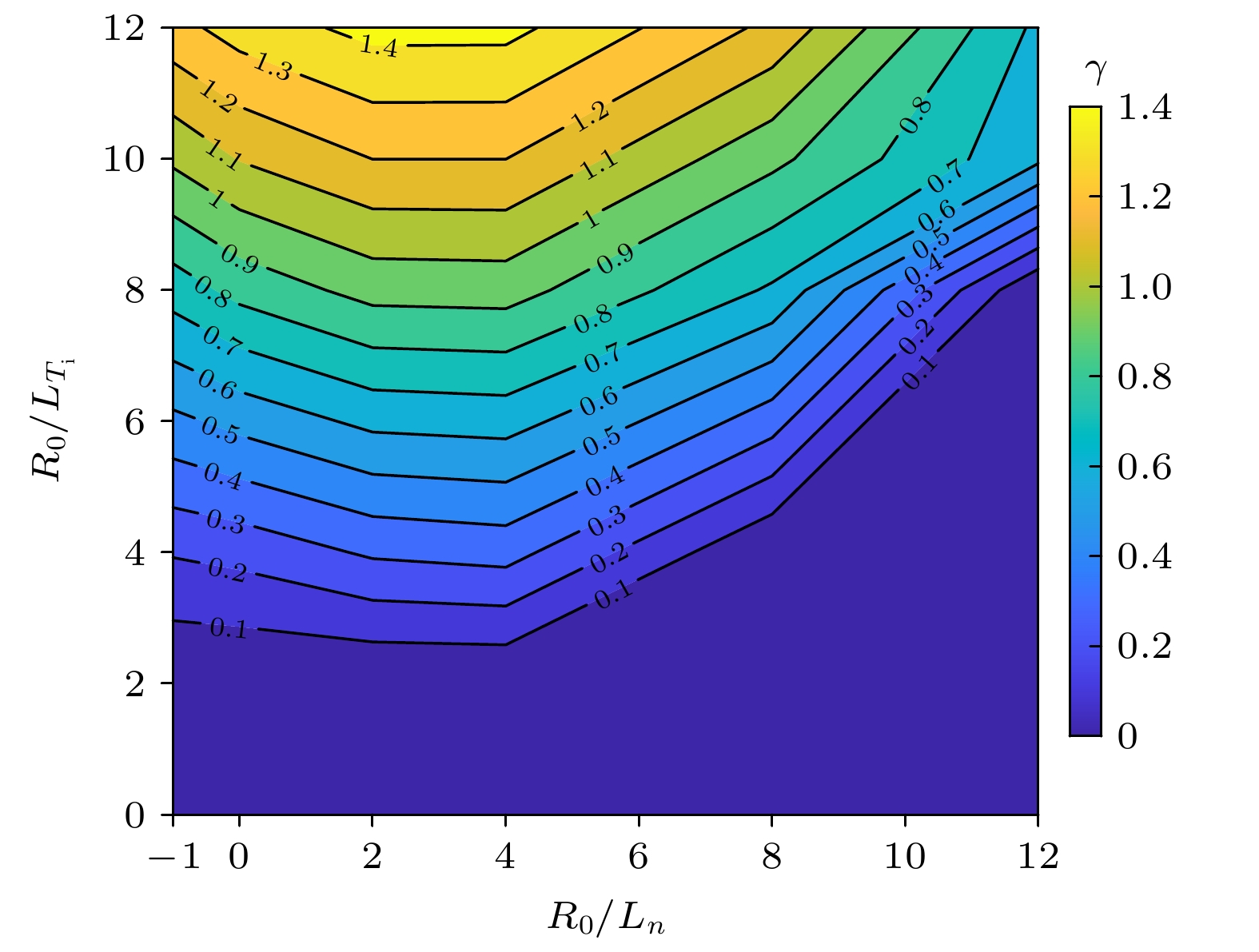
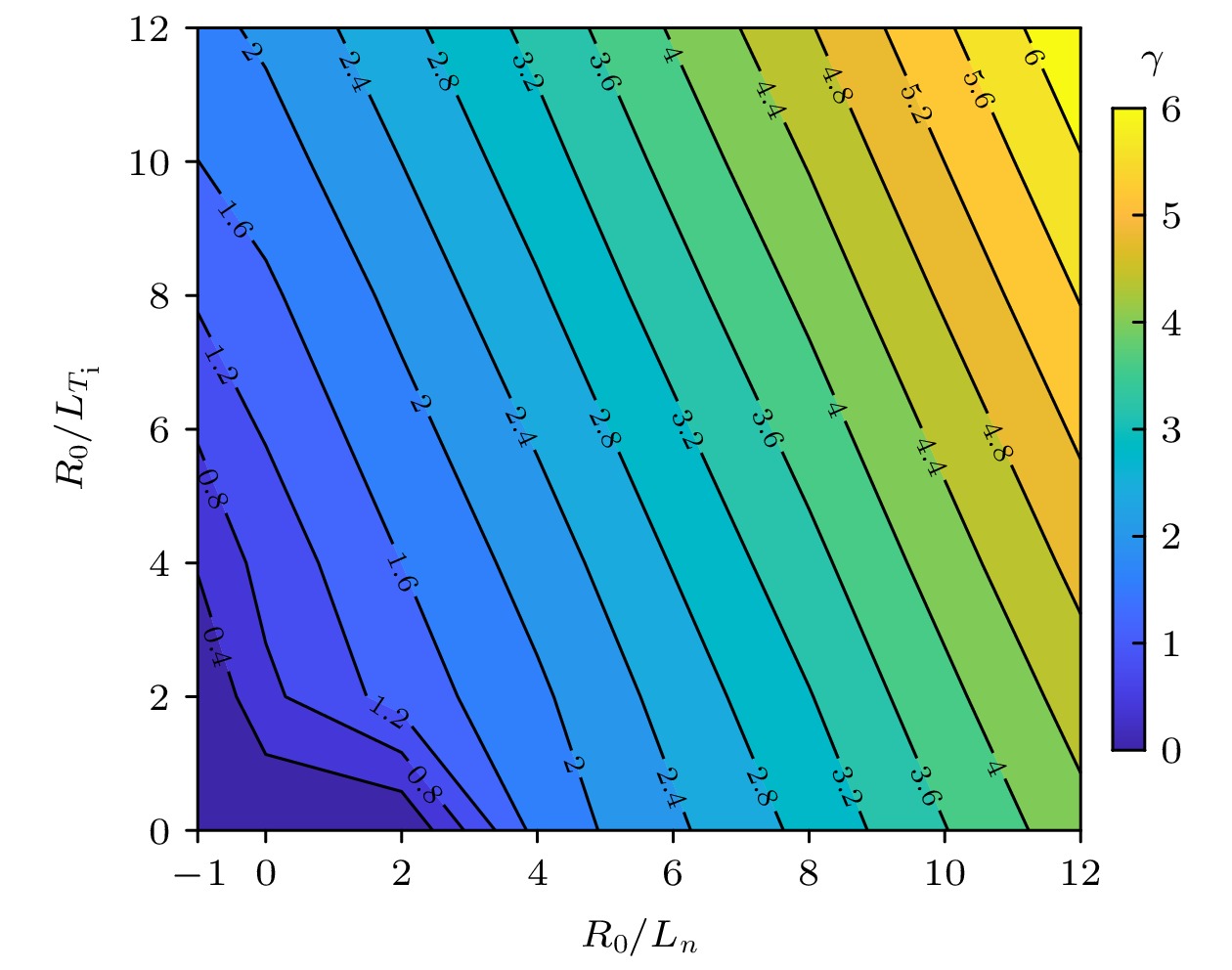
$ {R}_{0}/{L}_{n}=2 $ . Here,$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}={R}_{0}/{L}_{{T}_{\mathrm{i}}} $ .
图 5 考虑捕获电子效应后ITG/TE-ITG最大增长率与密度梯度和温度梯度的关系, 其中
$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}={R}_{0}/{L}_{{T}_{\mathrm{i}}} $ Figure 5. Contour map of the maximum growth rate of kinetic ITG/TE-ITG mode vs.
$ {R}_{0}/{L}_{n} $ and$ {R}_{0}/{L}_{T} $ . Here,${R}_{0}/ {L}_{{T}_{\mathrm{e}}} $ $ ={R}_{0}/{L}_{{T}_{\mathrm{i}}}$ .
图 6 考虑捕获电子效应后ITG的增长率(a)和频率波数谱(b), 其中
$ {R}_{0}/{L}_{n}=2 $ ,$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ Figure 6. Growth rate (a) and real frequency spectra (b) of kinetic ITG for
$ {R}_{0}/{L}_{n}=2 $ and$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ .
图 7 考虑捕获电子效应后ITG最大增长率与密度梯度和离子温度梯度的关系, 其中
$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ Figure 7. Contour map of the maximum growth rate of kinetic ITG vs.
$ {R}_{0}/{L}_{n} $ and$ {R}_{0}/{L}_{{T}_{\mathrm{i}}} $ . Here,$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ .
图 8 当波数
$ {k}_{y}{\rho }_{\mathrm{i}}=1.0 $ 时增长率(a)与频率(b)随比压的变化(其中,$ {R}_{0}/{L}_{n}=2 $ ,$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}={R}_{0}/{L}_{{T}_{\mathrm{i}}}=8 $ ), 图(a)中的箭头是从ITG转变为KBM的转变点Figure 8. Growth rates (a) and real frequencies (b) vs.
$ \beta $ for$ {R}_{0}/{L}_{n}=2 $ and$ {R}_{0}/{L}_{{T}_{\mathrm{i}}}={R}_{0}/{{L}}_{{{T}}_{\mathrm{e}}}=8 $ at$ {k}_{y}{\rho }_{\mathrm{i}}=1.0 $ . The arrow is plotted in panel (a) to point the transition point from ITG to KBM.
图 9 取
$\beta =1{\text{%}}$ 时, KBM的增长率(a)和频率(b)波数谱, 其中$ {R}_{0}/{L}_{n}=2 $ ,$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ Figure 9. Growth rate (a) and real frequency spectra (b) of KBM for
$ {R}_{0}/{L}_{n}=2 $ and$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ . Here,$\beta =1{\text{%}}$ .
图 10 取
$\beta =1{\text{%}}$ 时, KBM的最大增长率与密度梯度和离子温度梯度的关系, 其中$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ Figure 10. Contour map of the maximum growth rate of KBM vs.
$ {R}_{0}/{L}_{n} $ and$ {R}_{0}/{L}_{{T}_{\mathrm{i}}} $ . Here,$ {R}_{0}/{L}_{{T}_{\mathrm{e}}}=8 $ and$\beta =1{\text{%}}$ . -
[1] Xu Y 2016 Matter Radiat. Extremes 1 192
Google Scholar
[2] Ho D D M 1987 Phys. Fluids 30 442
Google Scholar
[3] Boozer A H 1995 Plasma Phys. Controlled Fusion 37 A103
Google Scholar
[4] Subbotin A A, Mikhailov M I, Shafranov V D, Isaev M Yu, Nührenberg C, Nührenberg J, Zille R, Nemov V V, Kasilov SV, Kalyuzhnyj V N 2006 Nucl. Fusion 46 921
Google Scholar
[5] Garabedian P 1996 Phys. Plasmas 3 2483
Google Scholar
[6] Shimizu A, Liu H F, Isobe M, Okamura S, Nishimura S, Suzuki C, Xu Y, Zhang X, Liu B, Huang J, Wang X Q, Liu H, Tang C J, CFQS team 2018 Plasma Fusion Res. 13 3403123
Google Scholar
[7] Zarnstorff M C, Berry L A, Brooks A, Fredrickson1 E, Fu G Y, Hirshman S, Hudson, Ku L P, Lazarus E, Mikkelsen D, Monticello D, Neilson G H, Pomphrey N, Reiman A, Spong D, Strickler D, Boozer A, Cooper W A, Goldston R, Hatcher R, Isaev M, Kessel C, Ewandowski J L, Lyon J F, Merkel P, Mynick H, Nelson B E, Nuehrenberg C, Redi M, Reiersen W, Rutherford P, Sanchez R, Schmidt J, White R B 2001 Plasma Phys. Controlled Fusion 43 A237
Google Scholar
[8] Okamura S, Matsuoka K, Nishimura S, Isobe M, Nomura I, Suzuki C, Shimizu A, Murakami S, Nakajima N, Yokoyama M 2001 Nucl. Fusion 41 1865
Google Scholar
[9] Liu H F, Shimizu A, Isobe M, Okamura S, Nishimura S, Suzuki C, Xu Y, Zhang X, Liu B, Huang J, Wang X Q, Liu H, Tang C J, Yin D P, Wan Y, CFQS team 2018 Plasma Fusion Res. 13 3405067
Google Scholar
[10] Isobe M, Shimizu A, Liu H F, Liu H, Xiong G Z, Yin D P, Ogawa K, Yoshimura Y, Nakata M, Kinoshita S, Okamura S, tang C J, Xu Y, CFQS Team 2019 Plasma Fusion Res. 14 3402074
Google Scholar
[11] Liu H F, Shimizu A, Xu Y, Okamura S, Kinoshita S, Isobe M, Li Y B, Xiong G Z, Wang X Q, Huang J, Cheng J, Liu H, Zhang X, Yin D P, Wang Y, Murase T, Nakagawa S, Tang C J 2021 Nucl. Fusion 61 016014
Google Scholar
[12] Wang X Q, Xu Y, Shimizu A, Isobe M, Okamura S, Todo Y, Wang H, Liu H F, Huang J, Zhang X, Liu H, Cheng J, Tang C J, CFQS team 2021 Nucl. Fusion 61 036021
Google Scholar
[13] Horton W 1999 Rev. Mod. Phys. 71 735
Google Scholar
[14] Watanabe T H, Sugama H 2006 Nucl. Fusion 46 24
Google Scholar
[15] Nakata M, Nunami M, Sugama H 2017 Phys. Rev. Lett. 118 165002
Google Scholar
[16] Antonsen T M, Lane B 1980 Phys. Fluids 23 1205
Google Scholar
[17] Nakata M, Honda M, Yoshida M, Urano H, Nunami M, Maeyama S, Watanabe T H, Sugama H 2016 Nucl. Fusion 56 086010
Google Scholar
[18] Beer M A, Cowley S C, Hammett G W 1995 Phys. Plasmas 2 2687
Google Scholar
[19] Romanelli M, Bourdelle C, Dorland W 2004 Phys. Plasmas 11 3845
Google Scholar
[20] Du H R, Jhang H, Hahm T S, Dong J Q, Wang Z X 2017 Phys. Plasmas 24 122501
Google Scholar
[21] 沈勇, 董家齐, 徐红兵 2018 67 195203
Google Scholar
Shen Y, Dong J Q, Xu H B 2018 Acta Phys. Sin. 67 195203
Google Scholar
[22] Baumgaertel J A, Hammett G W, Mikkelsen D R, Nunami M, Xanthopoulos P 2012 Phys. Plasmas 19 122306
Google Scholar
[23] Dominguez R R, Waltz R E 1988 Phys. Fluids 31 3147
Google Scholar
[24] Nunami M, Watanabe T H, Sugama H, Tanaka K 2011 Plasma Fusion Res. 6 1403001
Google Scholar
[25] Alcusón J A, Xanthopoulos P, Plunk G G, Helander P, Wilms F, Turkin Y, Stechow A von, Grulke O 2020 Plasma Phys. Controlled Fusion 62 035005
Google Scholar
[26] 罗一鸣, 王占辉, 陈佳乐, 吴雪科, 付彩龙, 何小雪, 刘亮, 杨曾辰, 李永高, 高金明, 杜华荣, 昆仑集成模拟设计组 2022 71 075201
Google Scholar
Luo Y M, Wang Z H, Chen J L, Wu X K, Fu C L, He X X, Liu L, Yang Z C, Li Y G, Gao J M, Du H R, Kulun Integrated Simulation and Design Group 2022 Acta Phys. Sin. 71 075201
Google Scholar
[27] Mahmood M A, Rafiq T, Persson M, Weiland J 2009 Phys. Plasmas 16 022503
Google Scholar
[28] Dong J Q, Mahajan S M, Horton W 1997 Phys. Plasmas 4 755
Google Scholar
[29] Peeters A G, Angioni C, Apostoliceanu M, Jenko F, Ryter F, the ASDEX Upgrade team 2005 Phys. Plasmas 12 022505
Google Scholar
[30] Sandberg I, Isliker H, Pavlenko V P 2007 Phys. Plasmas 14 092504
Google Scholar
[31] Qi L, Kwon J, Hahm T S, Jo G 2016 Phys. Plasmas 23 062513
Google Scholar
[32] Malinov P, Zonca F 2005 J. Plasma Phys. 71 301
Google Scholar
[33] Kim J Y, Han H S 2017 Phys. Plasmas 24 072501
Google Scholar
[34] Pueschel M J, Jenko F 2010 Phys. Plasmas 17 062307
Google Scholar
[35] Xie H S, Lu Z X, Li B 2018 Phys. Plasmas 25 072106
Google Scholar
[36] Aleynikova K, Zocco A 2017 Phys. Plasmas 24 092106
Google Scholar
[37] Turnbull A D, Strait E J, Heidbrink W W, Chu M S, Duong H H, Greene J M, Lao L L, Taylor T S, Thompson S J 1993 Phys. Fluids B 5 2546
Google Scholar
[38] Dong J, Chen L, Zonca F 1999 Nucl. Fusion 39 1041
Google Scholar
[39] 谢华生 2015 博士学位论文 (杭州: 浙江大学)
Xie H S 2015 Ph. D. Dissertation (Hangzhou: Zhejiang University) (in Chinese)
[40] Aleynikova K, Zocco1 A, Xanthopoulos1 P, Helander1 P, Nührenberg C 2018 J. Plasma Phys. 84 745840602
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5738
- PDF Downloads: 89
- Cited By: 0
