-
Circular cross-section plasma is the most basic form of tokamak plasma and the fundamental configuration for magnetic confinement fusion experiments. Based on the HL-2A limiter discharge experiments, the magnetohydrodynamic (MHD) equilibrium and MHD instability of circular cross-section tokamak plasmas are investigated in this work. The results show that when $ {q}_{0}=0.95 $, the internal kink mode of $ m/n=1/1 $ is always unstable. The increase in plasma $ \beta $ (the ratio of thermal pressure to magnetic pressure) can lead to the appearance of external kink modes. The combination of axial safety factor $ {q}_{0} $ and edge safety factor $ {q}_{{\mathrm{a}}} $ determines the equilibrium configuration of the plasma and also affects the MHD stability of the equilibrium, but its growth rate is also related to the size of $ \beta $. Under the condition of $ {q}_{{\mathrm{a}}} > 2 $ and $ {q}_{0} $ slightly greater than $ 1 $, the internal kink mode and surface kink mode can be easily stabilized. However the plasma becomes unstable again and the instability intensity increases as $ {q}_{0} $ continues to increase when $ {q}_{0} $ exceeds $ 1 $. As the poloidal specific pressure ($ {\beta }_{{\mathrm{p}}} $) increases, the MHD instability develops, the equilibrium configuration of MHD elongates laterally, and the Shafranov displacement increases, which in turn has the effect on suppressing instability. Calculations have shown that the maximum $ \beta $ value imposed by the ideal MHD mode in a plasma with free boundary in tokamak experiments is proportional to the normalized current $ {I}_{{\mathrm{N}}} $ ($ {I}_{{\mathrm{N}}}={I}_{{\mathrm{p}}}\left({\mathrm{M}}{\mathrm{A}}\right)/a\left({\mathrm{m}}\right){B}_{0}\left({\mathrm{T}}\right) $), and the maximum specific pressure $ \beta \left({\mathrm{m}}{\mathrm{a}}{\mathrm{x}}\right) $ is calibrated to be $ ~2.01{I}_{{\mathrm{N}}},{\mathrm{ }}{\mathrm{i}}. {\mathrm{e}}. $ $ \beta \left({\mathrm{m}}{\mathrm{a}}{\mathrm{x}}\right)~2.01{I}_{{\mathrm{N}}} $. The operational $ \beta $ limit of HL-2A circular cross-section plasma is approximately $ {\beta }_{{\mathrm{N}}}^{{\mathrm{c}}}\approx 2.0 $. Too high a value of $ {q}_{0} $ is not conducive to MHD stability and leads the $ \beta $ limit value to decrease. When $ {q}_{0}=1.3 $, we obtain a maximum value of $ {\beta }_{{\mathrm{N}}} $ of approximately $ 1.8 $. Finally, based on the existing circular cross-section plasma, some key factors affecting the operational $ \beta $ and the relationship between the achievable high $ \beta $ limit and the calculated ideal $ \beta $ limit are discussed.
-
Keywords:
- circular cross-section plasma /
- magnetohydrodynamic equilibrium /
- magnetohydrodynamic instability /
- kink mode /
- $ \beta $ limit
-
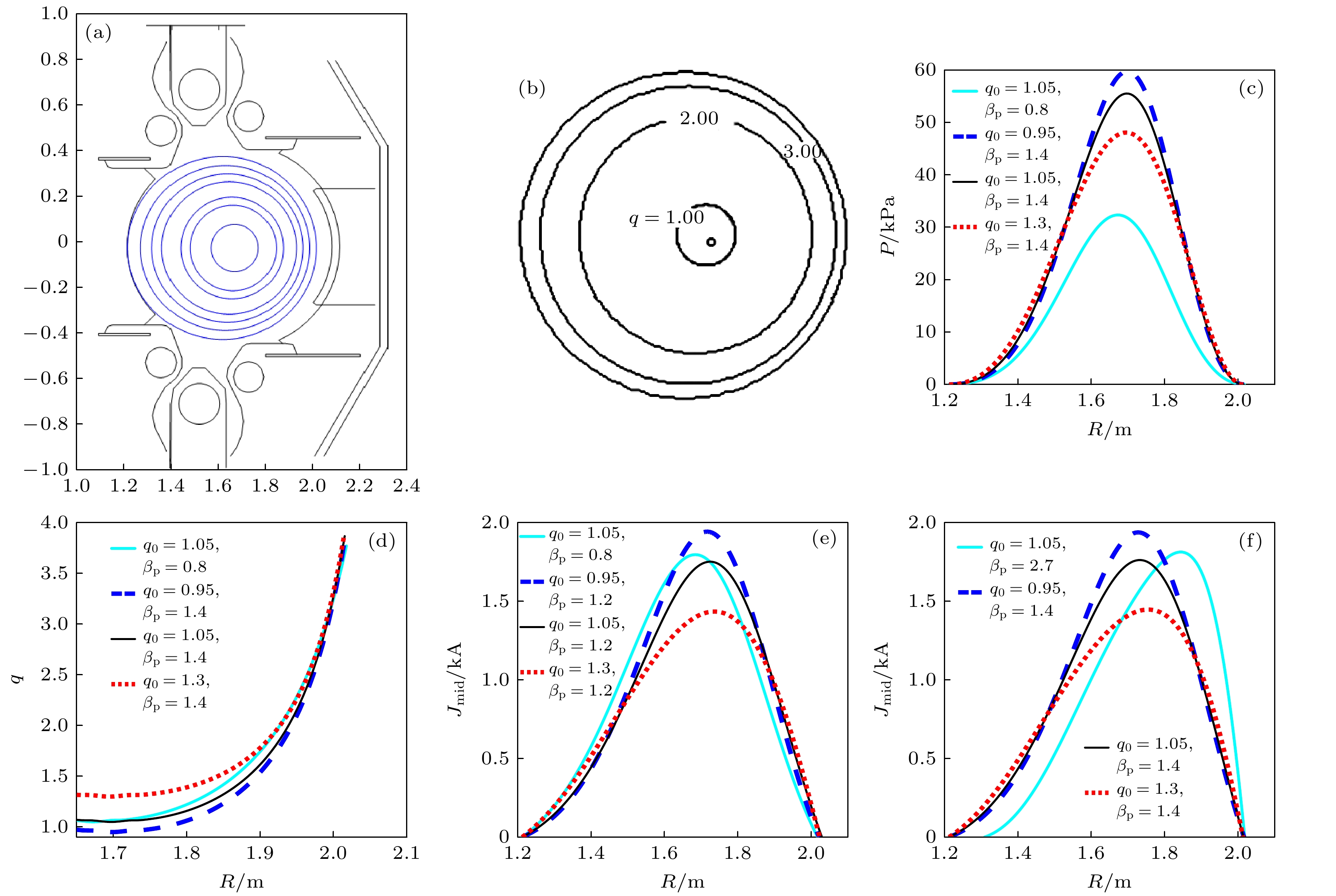
图 1 在4206次放电中, $ {q}_{0}=0.95 $, $ {\beta }_{{\mathrm{p}}}=0.8 $时, 装置与等离子体平衡位形(a)和等离子体平衡磁面结构(b), 以及不同$ {q}_{0} $与$ {\beta }_{{\mathrm{p}}} $下的(c)压强剖面、(d) $ q $剖面和(e), (f)电流密度($ {J}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{d}}} $)剖面
Figure 1. (a) Equilibrium configuration constructed and (b) mapped flux surfaces for $ {q}_{0}=0.95 $ and $ {\beta }_{{\mathrm{p}}}=0.8 $ in HL-2A discharge #4206, and (c) pressure ($ p $) profile, (d) $ q $ profile and (e), (f) current density ($ {J}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{d}}} $) profiles for different $ {q}_{0} $ and $ {\beta }_{{\mathrm{p}}} $.
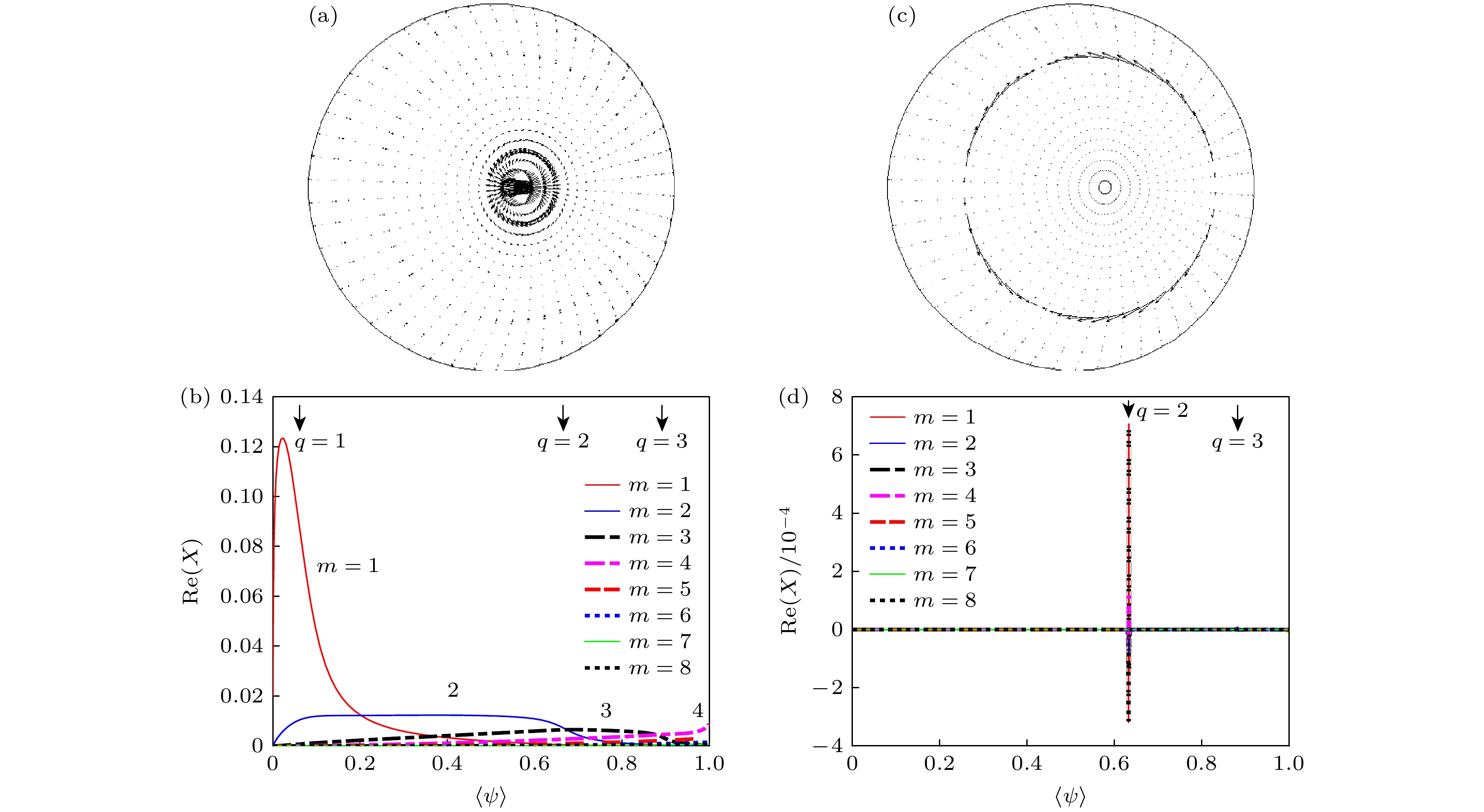
图 2 在4206次放电中, $ {\beta }_{{\mathrm{p}}}=1.2 $时, 不同$ {q}_{0} $对应的$ n=1 $扭曲模扰动位移在极向截面的投影(a), (c)及模的傅里叶分解图(b), (d) (a), (b) $ {q}_{0}=0.95 $; (c), (d) $ {q}_{0}=1.05 $. 横轴$ \left\langle{\psi }\right\rangle $代表归一化磁通
Figure 2. At $ {\beta }_{{\mathrm{p}}}=1.2 $ for discharge #4206, the mode displacement vectors projected onto the poloidal plane (a), (c) and the Fourier decomposition of the normal displacement (b), (d): (a), (b) $ {q}_{0}=0.95 $; (c), (d) $ {q}_{0}=1.05 $. The horizontal axis $ \left\langle{\psi }\right\rangle $ represents the normalized magnetic flux.
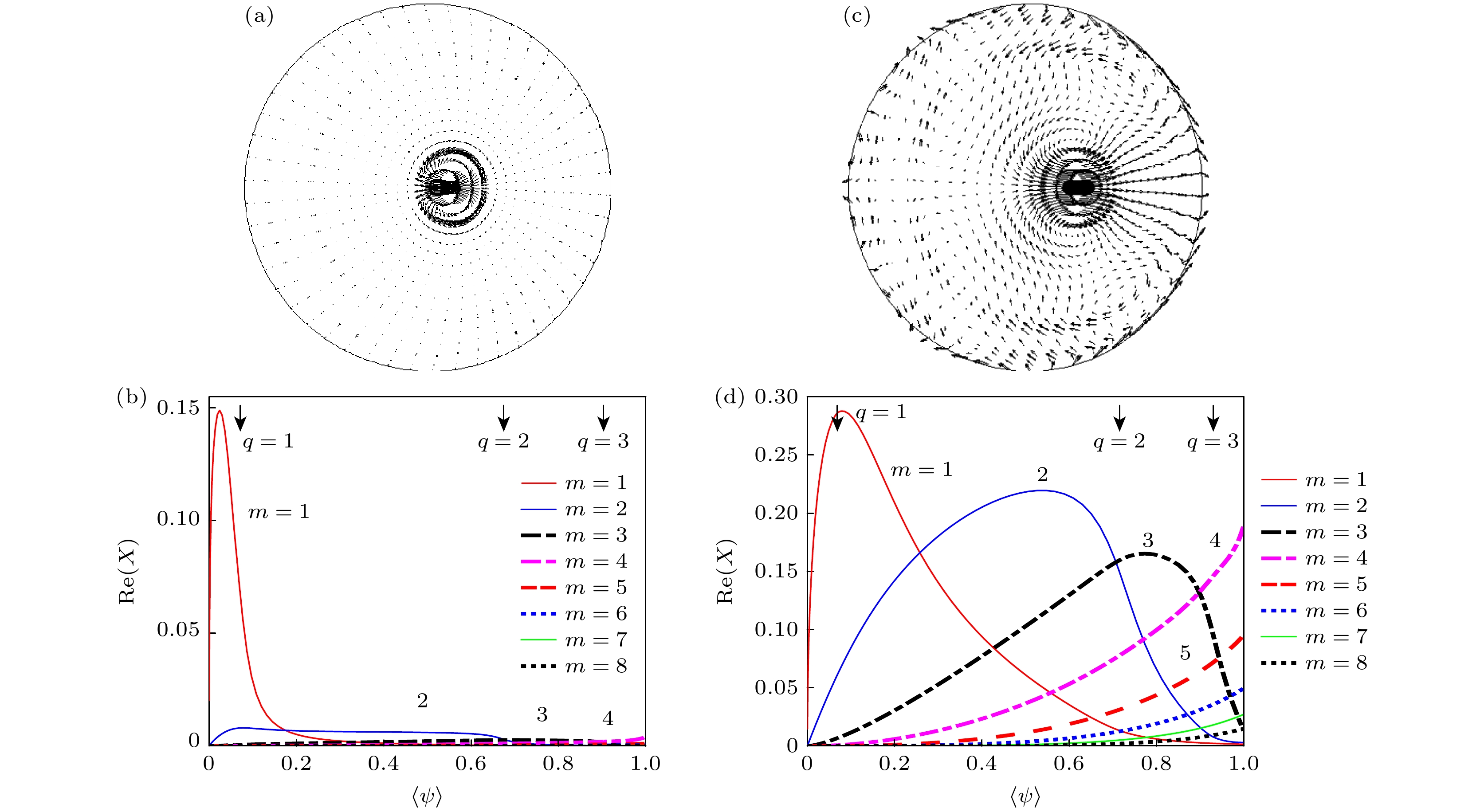
图 3 在4044次放电中, $ {q}_{0}=0.95 $时, 不同$ {q}_{0} $对应的模扰动位移在极向截面的投影(a), (c)及模的傅里叶分解图(b), (d) (a), (b) $ {\beta }_{{\mathrm{p}}}=0.8 $; (c), (d) $ {\beta }_{{\mathrm{p}}}=1.8 $
Figure 3. Unstable kink mode for limiter discharge with $ {q}_{0}=0.95 $ for discharge #4044, the mode displacement vectors projected onto the poloidal plane (a), (c) and Fourier decomposition of the normal displacement (b), (d) $ : $ (a), (b) $ {\beta }_{{\mathrm{p}}}=0.8 $; (c), (d) $ {\beta }_{{\mathrm{p}}}=1.8 $
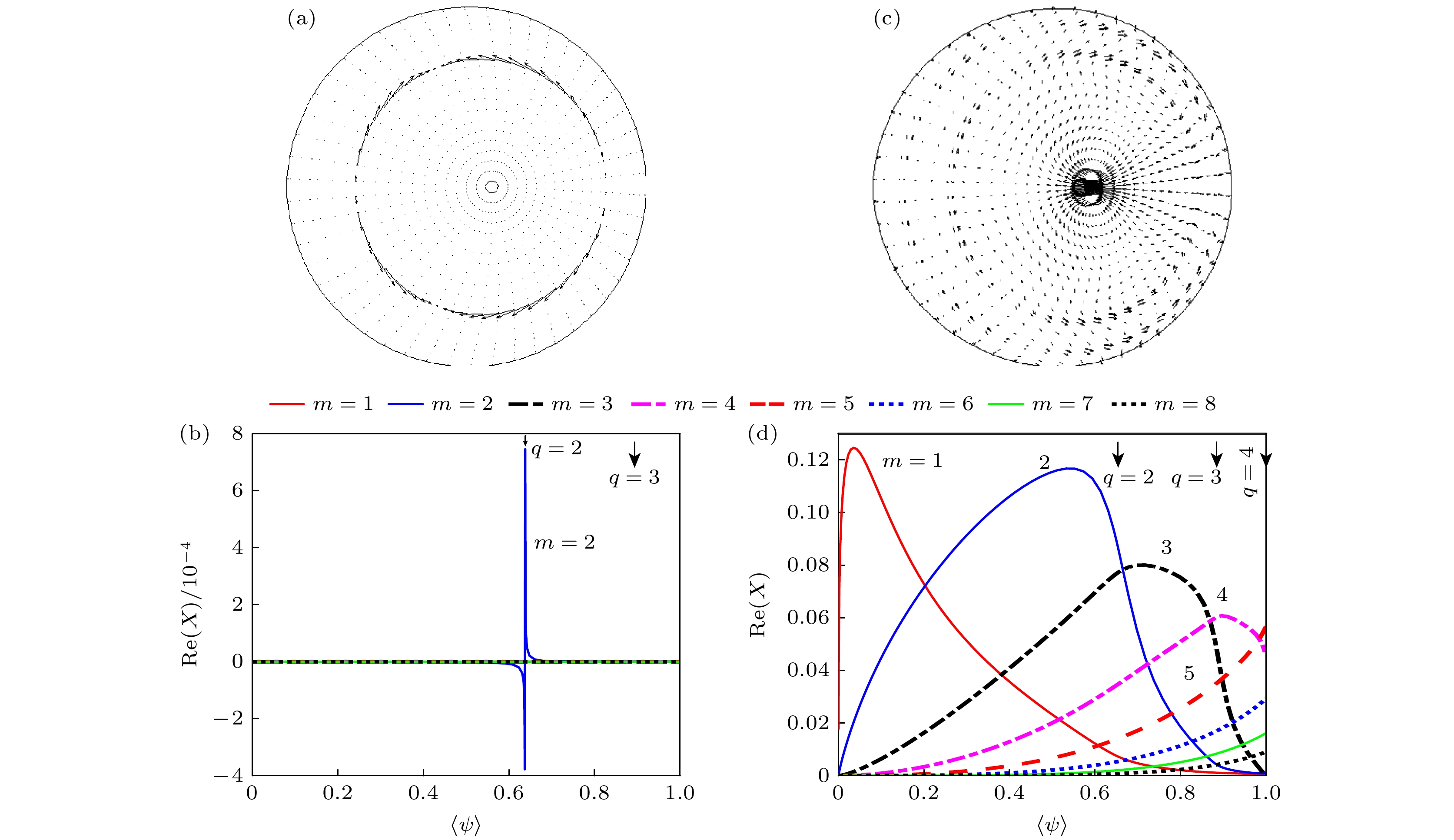
图 4 在4044次放电中, $ {q}_{0}=1.05 $时, 不同$ {q}_{0} $对应的模扰动位移在极向截面的投影及模的傅里叶分解图 (a), (b) $ {\beta }_{{\mathrm{p}}}=0.8 $; (c), (d) $ {\beta }_{{\mathrm{p}}}=1.8 $
Figure 4. For discharge #4044, mode displacement vectors projected onto the poloidal plane (a), (c) with $ {q}_{0}=1.05 $and Fourier decomposition of the normal displacement (b), (d) $ :\left({\mathrm{a}}\right), {\mathrm{ }}\left({\mathrm{b}}\right){\beta }_{{\mathrm{p}}}=0.8;{\mathrm{ }}\left({\mathrm{c}}\right), {\mathrm{ }}\left({\mathrm{d}}\right){\beta }_{{\mathrm{p}}}=1.8 $.
图 5 在4206次放电中, $ {\beta }_{{\mathrm{p}}}=2 $时, (a), (b) $ {q}_{0}=0.95 $, (c), (d) $ {q}_{0}=1.05 $和(e), (f) $ {q}_{0}=1.3 $对应的$ n=1 $扭曲模扰动位移在极向截面的投影及模的傅里叶分解图
Figure 5. At $ {\beta }_{{\mathrm{p}}}=2 $ for discharge #4206, the mode displacement vectors projected onto the poloidal plane for $ {q}_{0}=0.95 $ (a), $ 1.05 $ (c) and $ 1.3 $ (e), and Fourier decomposition of the normal displacement for $ {q}_{0}=0.95 $ (b), $ 1.05 $ (d) and $ 1.3 $ (f).
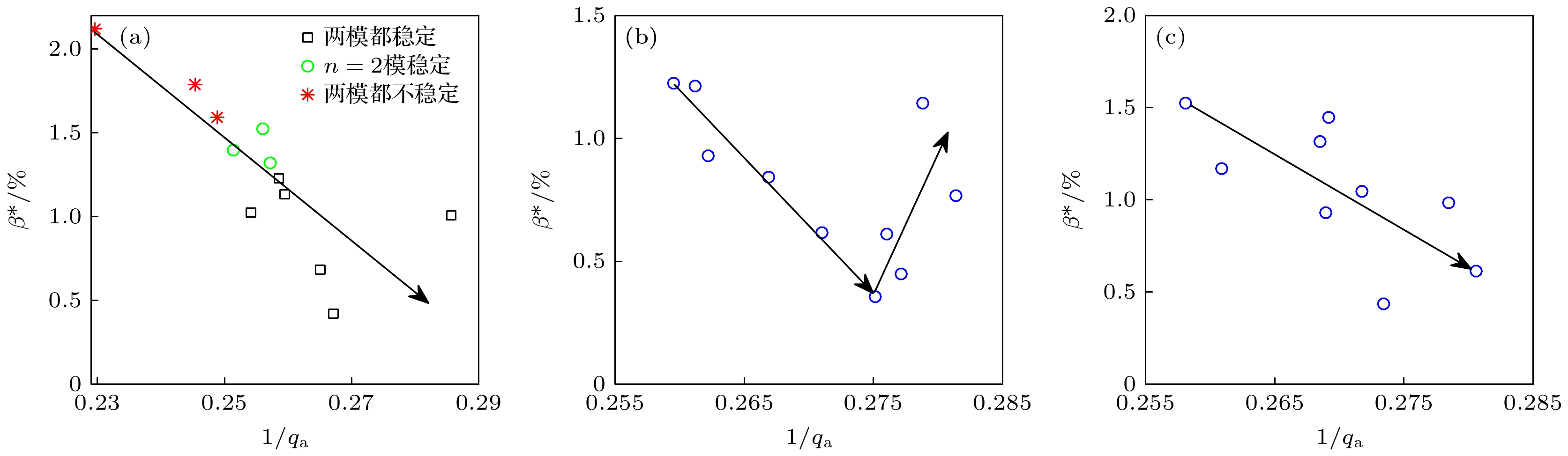
图 6 对典型的限制器类型放电 (a) 固定$ {q}_{0}=1.05 $时, $ 1/{q}_{{\mathrm{a}}} $-$ {\beta }^{*} $平面内的扭曲稳定性; (b)不固定$ {q}_{0} $时, 使$ n=1 $模稳定的最大$ {\beta }^{*} $和$ 1/{q}_{{\mathrm{a}}} $; (c)不固定$ {q}_{0} $时, 使$ n=2 $模稳定的最大$ {\beta }^{*} $和$ 1/{q}_{{\mathrm{a}}} $
Figure 6. For the typical limiter discharges: (a) Kink stabilities in $ 1/{q}_{{\mathrm{a}}} $-$ {\beta }^{*} $plane at fixed $ {q}_{0}=1.05 $; (b) $ {\beta }^{*} $ vs. $ {q}_{{\mathrm{a}}} $ at unfixed $ {q}_{0} $, here $ {\beta }^{*} $ is the maximum achievable one limited by $ n=1 $ kink; (c) $ {\beta }^{*} $ vs. $ {q}_{{\mathrm{a}}} $ at unfixed $ {q}_{0} $, here $ {\beta }^{*} $ is the maximum achievable one limited by $ n=2 $ kink. The solid lines with arrows indicate the change direction of $ {\beta }^{*} $ as $ {q}_{{\mathrm{a}}} $ increases.
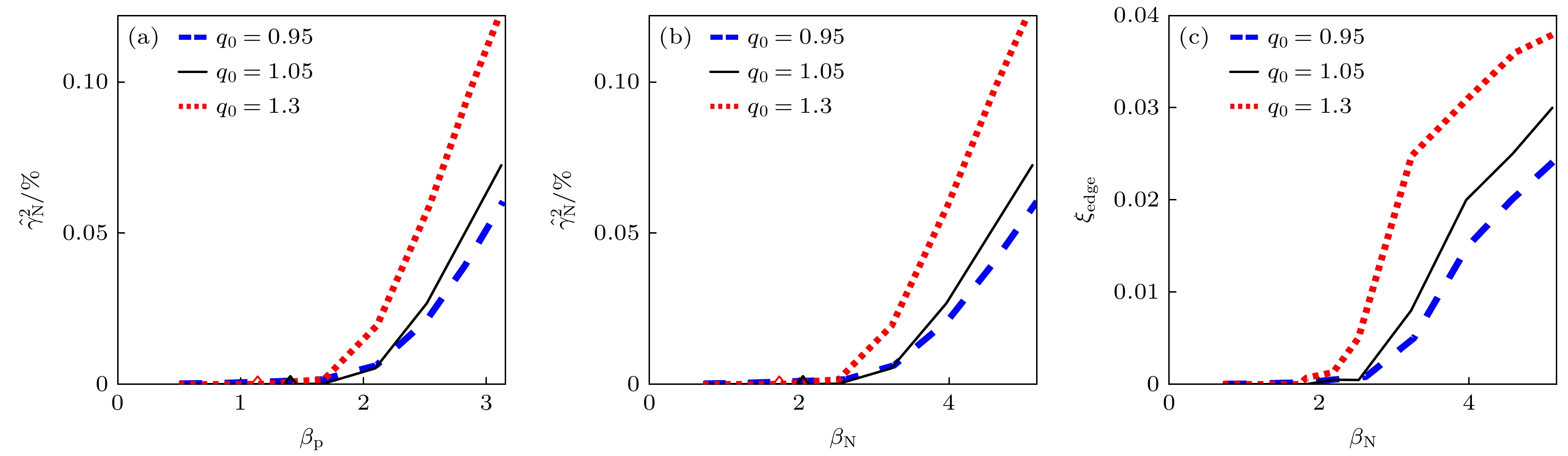
图 7 基于4044次放电的计算结果 (a), (b)归一化增长率的平方值$ {\widehat{\gamma }}_{{\mathrm{N}}}^{2} $对$ {\beta }_{{\mathrm{p}}} $和$ {\beta }_{{\mathrm{N}}} $的依赖; (c)边缘最大扰动位移随归一化比压的变化. 注意图中, $ {\beta }_{{\mathrm{p}}} $是计算的平衡位形的实际极向比压. 菱形符号表示临界点
Figure 7. Calculations were based on the data of discharge #4044: (a), (b) Square value of normalized mode growth rate $ {\widehat{\gamma }}_{{\mathrm{N}}}^{2} $ as functions of $ {\beta }_{{\mathrm{p}}} $ and $ {\beta }_{{\mathrm{N}}} $; (c) maximum edge normal displacement as functions of normalized. Note that βp is the actual polar specific pressure of the calculated equilibrium configuration. The rhombus symbol represents the critical point
-
[1] Buttery R J, Park J M, McClenaghan J T, Weisberg D, Canik J, Ferron J, Garofalo A, Holcomb C T, Leuer J, Snyder P B, The Atom Project Team 2021 Nucl. Fusion 61 046028
Google Scholar
[2] SarazinY, Hillairet J, Duchateau J L, Gaudimont K, Varennes R, Garbet X, Ghendrih Ph, Guirlet R, Pégourié B, Torre A 2020 Nucl. Fusion 60 016010
Google Scholar
[3] Hender T C, Wesley J C, Bialek J 2007 Nucl. Fusion 47 S128
Google Scholar
[4] Suzuki Y, Watanabe K Y, Sakakibara S 2020 Phys. Plasmas 27 102502
Google Scholar
[5] Liu Y, Chapman I T, Saarelma S, Gryaznevich M P, Hender T C, Howell D F, JET-EFDA contributors 2009 Plasma Phys. Controlled Fusion 51 115005
Google Scholar
[6] Wolf R C, Biel W, Bock M F M de, Finken K H, Günter S, Hogeweij G M D, Jachmich S, Jakubowski M W, Jaspers R J E, Krämer-Flecken A, Koslowski H R, Lehnen M, Liang Y, Unterberg B, Varshney S K, Hellermann M von, Yu Q, Zimmermann O, Abdullaev S S, Donné A J H, Samm U, Schweer B, Tokar M, Westerhof E, the TEXTOR Team 2005 Nucl. Fusion 45 1700
Google Scholar
[7] Zhao K J, Lan T, Dong J Q, Yan L W, Hong W Y, Yu C X, Liu A D, Qian J, Cheng J, Yu D L, Yang Q W, Ding X T, Liu Y, Pan C H 2006 Phys. Rev. Lett. 96 255004
Google Scholar
[8] Chen W, Ding X T, Yang Q W, Liu Yi, Ji X Q, Zhang Y P, Zhou J, Yuan G L, Sun H J, Li W, Zhou Y, Huang Y, Dong J Q, Feng B B, Song X M, Shi Z B, Liu Z T, Song X Y, Li L C, Duan X R, Liu Y (HL-2A team) 2010 Phys. Rev. Lett. 105 185004
Google Scholar
[9] Zhong W L, Shen Y, Zou X L, Gao J M, Shi Z B, Dong J Q, Duan X R, Xu M, Cui Z Y, Li Y G, Ji X Q , Yu D L, Cheng J, Xiao G L, Jiang M, Yang Z C, Zhang B Y, Shi P W, Liu Z T, Song X M, Ding X T, Liu Y (HL-2A Team1) 2016 Phys. Rev. Lett. 117 045001
[10] Xu M, Duan X R, Liu Yi, Song X M, Liu D Q, Wang Y Q, Lu B, Yang Q W, Zheng G Y, Ding X T, Dong J Q, Hao G Z, Zhong W L, Shi Z B, Yan L W, Zou X L, Liu Y Q, Chen W, Xiao G L, Zhang Y P, Jiang M, Hou Y M, …, the HL-2A Team 2019 Nucl. Fusion 59112017
[11] Piovesan P, Igochine V, Turco F, Ryan D A, Cianciosa M R, Liu Y Q, Marrelli L, Terranova D, Wilcox R S, Wingen A, Angioni C, Bock C, Chrystal C, Classen I, Dunne M, Ferraro N M, Fischer R, Gude A, Holcomb C T, Lebchy A, Luce T C, Maraschek M, McDermott R, Odstrčil T, Paz-Soldan C, Reich M, Sertoli M, Suttrop W, Taylor N Z, Weiland M, Willensdorfer M, The ASDEX Upgrade Team, The DIII-D Team and The EUROfusion MST1 Team 2009 Plasma Phys. Controlled Fusion 59 014027
[12] Igochine V, Piovesan P, Classen I G J, Dunne M, Gude A, Lauber P, Liu Y, Maraschek M, Marrelli L, Dermott R Mc, Reich M, Ryan D, Schneller M, Strumberger E, Suttrop W, Tardini G, Zohm H, The ASDEX Upgrade Team and The EUROfusion MST1 Team 2017 Nucl. Fusion 57 116027
Google Scholar
[13] Todd A M M, Manickam J, Okabayashi M, Chance M S, Grimm R C, Greene J M, Johnson J L 1979 Nucl. Fusion 19 743
Google Scholar
[14] Bernard L C, Helton F J, Moore R W, Todd T N 1983 Nucl. Fusion 23 1475.
Google Scholar
[15] 李正吉, 陈伟, 孙爱萍, 于利明, 王卓, 陈佳乐, 许健强, 李继全, 石中兵, 蒋敏, 李永高, 何小雪, 杨曾辰, 李鉴 2024 73 065202
Google Scholar
Li Z J, Chen W, Sun A P, Yu L M, Wang Z, Chen J L, Xu J Q, Li J Q, Shi Z B, Jiang M, Li YG, He X X, Yang Z C, Li J 2024 Acta Phys. Sin. 73 065202
Google Scholar
[16] 朱霄龙, 陈伟, 王丰, 王正汹 2023 72 215210
Google Scholar
Zhu X L, Chen W, Wang F, Wang Z X 2023 Acta Phys. Sin. 72 215210
Google Scholar
[17] Shen Y, Dong J Q, He H D, Li J, Wu N, Zhao K J, Deng W 2024 J. Phys. Soc. Jpn. 93 104501
Google Scholar
[18] Shen Y, Dong J Q, Pend X D, He H D, Li J X 2025 Phys. Rev. E 111 025208
Google Scholar
[19] Lao L L, John H St, Stambaugh R D, Kellman A G, Pfeiffer W 1985 Nucl. Fusion 25 1611
[20] Gruber R, Troyon F, Berger D, Bernard L C, Rousset S, Schreiber R, Kerner W, Schneider W, Roberts K V 1981 Comput. Phys. Commun. 21 323
Google Scholar
[21] Bernard L C, Helton F J, Moore R W 1981 Comput. Phys. Commu. 24 377
Google Scholar
[22] Lao L L, Strait E J, Taylor T S, Chu M S, Ozeki T, Howl W, Stambaugh R D, Burrell K H, Chance M S, DeBoo J C, Gohil P, Greene J M, Groebner R J, Kellman A G, Mahdavi M Ali, Osborne T H, Porter G, Turnbull A D 1989 Plasma Phys. Controlled Fusion 31 509
Google Scholar
[23] Aydemir A Y, Kim J Y, Park B H, Seol J 2015 Phys. Plasmas 22 032304
Google Scholar
[24] Bondeson A, Vlad G, Léutjens H 1992 Phys. Fluids B 4 1889
Google Scholar
[25] Turnbull AD, Pearlstein LD, Bulmer . H, Lao LL, Haye RJ La 1999 Nucl. Fusion 39 1557
[26] Kerner W, Gruber R, Troyon F 1980 Phys. Rev. Lett. 44 536
Google Scholar
[27] Troyon F, Gruber R, Saurenmann H, Semenzato S, Succi S 1984 Plasma Phys. Controlled Fusion 26 209
Google Scholar
[28] Troyon F, Gruber R 1985 Phys. Lett. 110A 29
[29] Bondeson A, Liu D H, Söldner F X, Persson M, Baranov Yu F, Huysmans G T A 1999 Nucl. Fusion 39 1523
Google Scholar
[30] 沈勇, 董家齐, 何宏达, 潘卫, 郝广周 2023 72 035203
Google Scholar
Shen Y, Dong J Q, He H D, Pan W, Hao G Z 2023 Acta Phys. Sin. 72 035203
Google Scholar
[31] Liu Y, Kirk A, Keeling D L, Kogan L, Du X D, Li L, Piron L, Ryan D A, Turnbull A D 2021 Nucl. Fusion 61 116022.
Google Scholar
[32] Wang S, Liu Y Q, Xia G L, Song X M, Hao G Z, Li L, Li B, Zhang N, Dong G Q, Bai X, Zheng G Y 2021 Plasma Phys. Controlled Fusion 63 055019
Google Scholar
[33] Haye R J La, Politzer P A, Brennan D P 2008 Nucl. Fusion 48 015005
Google Scholar
[34] Taylor T S, John H St, Turnbull A D, Lin-Liu V R, Burrell K H, Chan V, Chu M S, Ferron J R, Lao L L, Haye R J La, Lazarus E A, Miller R L, Politzer P A, Schissel, Strait E J 1994 Plasma Phys. Controlled Fusion 36 B229
Google Scholar
[35] Turnbull A D, Brennan D P, Chu M S, Lao L L, Snyder P B 2005 Fusion Sci. Technol. 48 875
Google Scholar
[36] Li G Q, Xu X Q, Snyder P B, Turnbull A D, Xia T Y, Ma C H, Xi P W 2014 Phys. Plasmas 21 102511
Google Scholar
DownLoad:
Metrics
- Abstract views: 327
- PDF Downloads: 6
- Cited By: 0
