-
为了理解托卡马克装置中给定径向电场对离子温度梯度模(ITG)稳定性的影响, 基于非线性回旋动理学理论和气球模表象推导了环位形下包含径向电场引起的极向流和密度扰动影响的ITG的本征模方程, 并分别在长/短波长极限下研究了高能量粒子诱发测地声模(EGAM)所伴随的径向电场对ITG的本征频率、增长率和平行模结构的影响. 不仅对该本征模方程进行了理论研究, 还使用本征矩阵法对其进行数值求解, 以便对理论结果进行验证. 研究发现EGAM伴随的电场引起的极向转动会大幅降低ITG的增长率, 而极向模数m = 1的密度扰动对ITG的线性稳定性影响很小. 这一结果与一般认为的带状流通过极向流剪切抑制湍流的结果是一致的. 除此之外, 使用本文发展的一般性方法也可以研究高能量粒子激发的阿尔芬不稳定性与漂移波湍流通过阿尔芬不稳定性激发带状结构发生的间接非线性相互作用, 即带状结构所伴随的径向电场通过极向转动和密度扰动影响ITG的稳定性. 该间接非线性通道可以作为对主导背景等离子体输运的微观湍流和主导高能量粒子输运的阿尔芬不稳定性之间的直接相互作用通道的补充.
-
关键词:
- 离子温度梯度模 /
- 径向电场 /
- 高能量粒子诱发测地声模 /
- 非线性回旋动理学理论
To understand the effect of given radial electric field on ion-temperature gradient driven mode (ITG) stability in tokamak plasmas, we derive the eigenmode equation for ITG including the poloidal rotation and density modulation associated with radial electric field by using nonlinear gyrokinetic theory. The equation is solved for the eigenfrequency, growth rate and parallel mode structure of ITG both in short- and long-wavelength limit with energetic-particle-induced geodesic acoustic mode (EGAM) as a specific form. The eigenmode equation is not only solved analytically, but also solved numerically to validate the analytic solutions. It is found that, the radial electric field induced poloidal rotation can significantly stabilize ITG, while the density perturbation of the radial electric field may slightly distort the ITG parallel mode structure, but has little effect on ITG stability. The result is consistent with the common picture of turbulence suppression by poloidal shear flow. The general model is also applicable to the investigation of the indirect interaction of ITG and energetic particle driven Alfvén instabilities via zonal structures generation, by introducing poloidal rotation and density modulation associated with zonal structures spontaneously excited by Alfvén instabilities. The indirect channel is supplement to the direct interaction of microturbulences and energetic particle driven Alfvén instabilities.-
Keywords:
- ion-temperature gradient driven mode /
- radial electric field /
- energetic-particle induced geodesic acoustic mode /
- nonlinear gyrokinetic theory
[1] Horton W 1999 Rev. Mod. Phys. 71 735
Google Scholar
[2] Lin Z H, Hahm T S, Lee W W, Tang W, White R 1998 Science 281 1835
Google Scholar
[3] Hahm T S, Beer M, Lin Z H, Hammett G, Lee W W, Tang W 1999 Phys. Plasmas 6 922
Google Scholar
[4] Chen L, Lin Z H, White R 2000 Phys. Plasmas 7 3129
Google Scholar
[5] Zonca F, Chen L 2008 Europhys. Lett. 83 35001
Google Scholar
[6] Nazikian R, Fu G Y, Austin M, Berk H, Budny R, Gorelenkov N, Heidbrink W, Holcomb C, Kramer G, McKee G, Makowski M, Solomon W, Shafer M, Strait E, Van Zeeland M 2008 Phys. Rev. Lett. 101 185001
Google Scholar
[7] Fu G Y 2008 Phys. Rev. Lett. 101 185002
Google Scholar
[8] Qiu Z Y, Zonca F, Chen L 2010 Plasma Phys. Control. Fusion 52 095003
Google Scholar
[9] Berk H, Zhou T 2010 Nuclear Fusion 50 035007
Google Scholar
[10] Qiu Z Y, Chen L, Zonca F, Chen W 2018 Phys. Rev. Lett. 120 135001
Google Scholar
[11] Zarzoso D, Sarazin Y, Garbet X, Dumont R, Strugarek A, Abiteboul J, Cartier-Michaud T, Dif-Pradalier G, Ghendrih P, Grandgirard V, Latu G, Passeron C, Thomine O 2013 Phys. Rev. Lett. 110 125002
Google Scholar
[12] Dimits A, Bateman G, Beer M, Cohen B, Dorland W, Hammett G, Kim C, Kinsey J, Kotschenreuther M, Kritz A, Lao L L, Mandrekas J, Nevins W, Parker S, Redd A, Shumaker D, Sydora R, Weiland J 2000 Phys. Plasmas 7 969
Google Scholar
[13] Qiu Z Y, Chen L, Zonca F 2014 Phys. Plasmas 21 022304
Google Scholar
[14] Qiu Z Y, Chen L, Zonca F 2015 Phys. Plasmas 22 042512
Google Scholar
[15] Tardini G, Hobirk J, Igochine V, Maggi C, Martin P, McCune D, Peeters A, Sips A, Stäbler A, Stober J, the ASDEX Upgrade Team 2007 Nuclear Fusion 47 280
Google Scholar
[16] Mantica P, Strintzi D, Tala T, Giroud C, Johnson T, Leggate H, Lerche E, Loarer T, Peeters A, Salmi A, Sharapov S, Van Eester D, de Vries P, Zabeo L, Zastrow K 2009 Phys. Rev. Lett. 102 175002
Google Scholar
[17] Romanelli M, Zocco A, Crisanti F, JET-EFDA Contributors 2010 Plasma Phys. Control. Fusion 52 045007
Google Scholar
[18] Garcia J, Challis C, Citrin J, Doerk H, Giruzzi G, Görler T, Jenko F, Maget P. JET Contributors 2015 Nuclear Fusion 55 053007
Google Scholar
[19] Citrin J, Jenko F, Mantica P, Told D, Bourdelle C, Garcia J, Haverkort J, Hogeweij G, Johnson T, Pueschel M 2013 Phys. Rev. Lett. 11 1
Google Scholar
[20] Chankin A, McCracken G 1993 Nuclear Fusion 33 1459
Google Scholar
[21] Cheng C Z, Chen L, Chance M 1985 Ann. Phys. 161 21
Google Scholar
[22] Chen L 1994 Phys. Plasmas 1 1519
Google Scholar
[23] Qiu Z Y, Chen L, Zonca F 2016 Nuclear Fusion 56 106013
Google Scholar
[24] Qiu Z Y, Chen L, Zonca F 2017 Nuclear Fusion 57 056017
Google Scholar
[25] Chen L, Qiu Z Y, Zonca F 2022 Nuclear Fusion 62 094001
Google Scholar
[26] Chen L, Qiu Z Y, Zonca F 2014 Europhys. Lett. 107 15003
Google Scholar
[27] Romanelli F, Zonca F 1993 Phys. Fluids B 5 4081
Google Scholar
[28] Chen L, Briguglio S, Romanelli F 1991 Phys. Fluids B 3 611
Google Scholar
[29] Chen N F, Hu H Y, Zhang X Y, Wei S Z, Qiu Z Y 2021 Phys. Plasmas 28 042505
Google Scholar
-
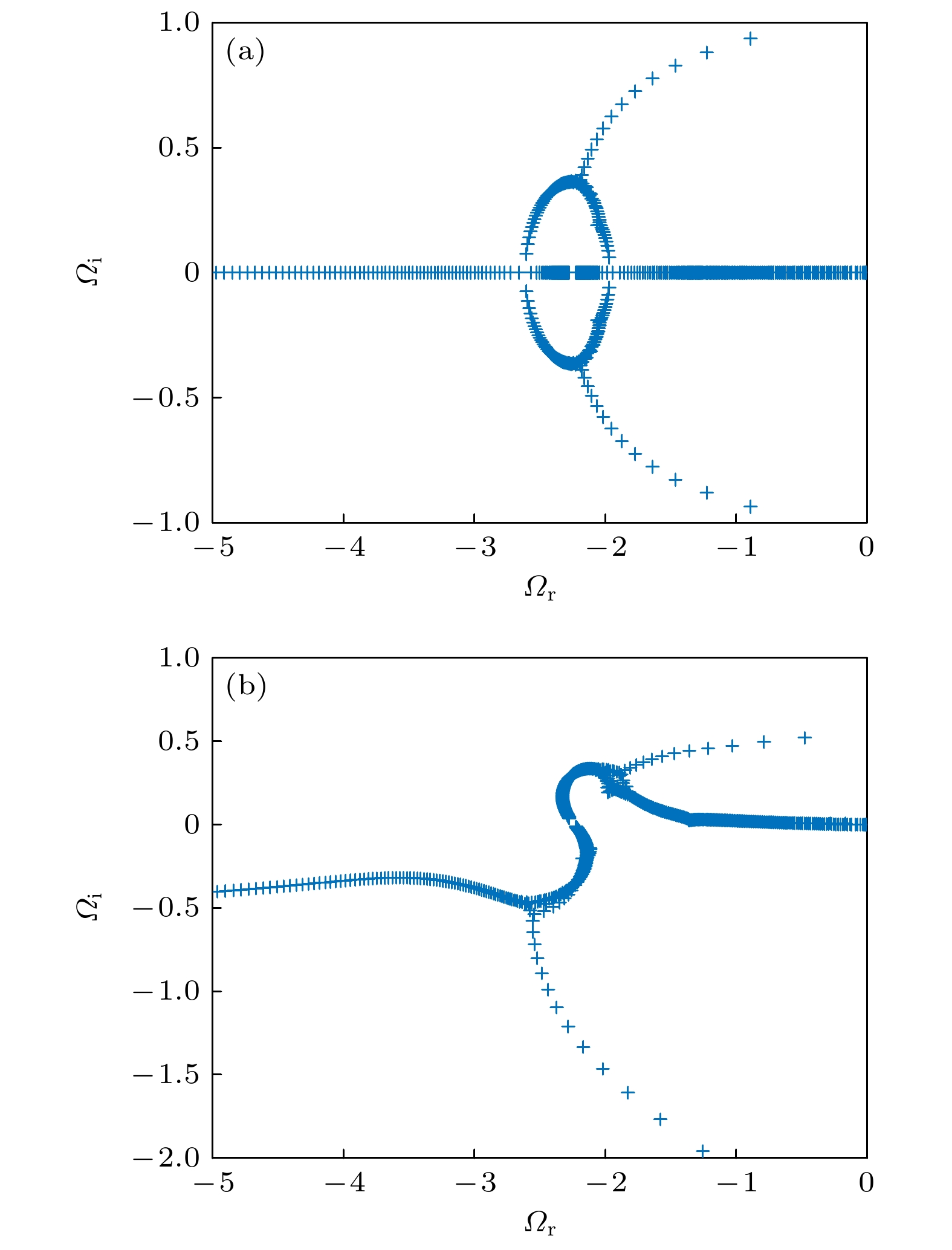
图 1 短波长极限下,
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}}=0 $ (a)和$ 0.1 $ (b)时, ITG本征值的实部($ \varOmega_{\rm r} $ )和虚部($ \varOmega_{\rm i} $ )的分布. 在两种情况下, 最不稳定的都是l = 0的基态Fig. 1. Distribution of the real (
$ \varOmega_{\rm r} $ ) and imaginary ($ \varOmega_{\rm i} $ ) parts of eigenvalues of ITG when$ e{{\text{δ}}}\phi_ {{\rm E}}/T_{{\rm i}}=0 $ (a) and$ 0.1 $ (b) in the short-wavelength limit. In both cases, the ground state with l = 0 is the most unstable eigenstate.
图 2 短波长极限下,
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}}=0.1 $ 和0时, ITG最不稳定的基态的平行模结构. 其中, 蓝色实线表示径向电场为零时ITG的模结构, 红色虚线表示有限径向电场时ITG的模结构Fig. 2. Mode structure of the most unstable mode of ITG. The blue solid and red dashed lines represent the cases with
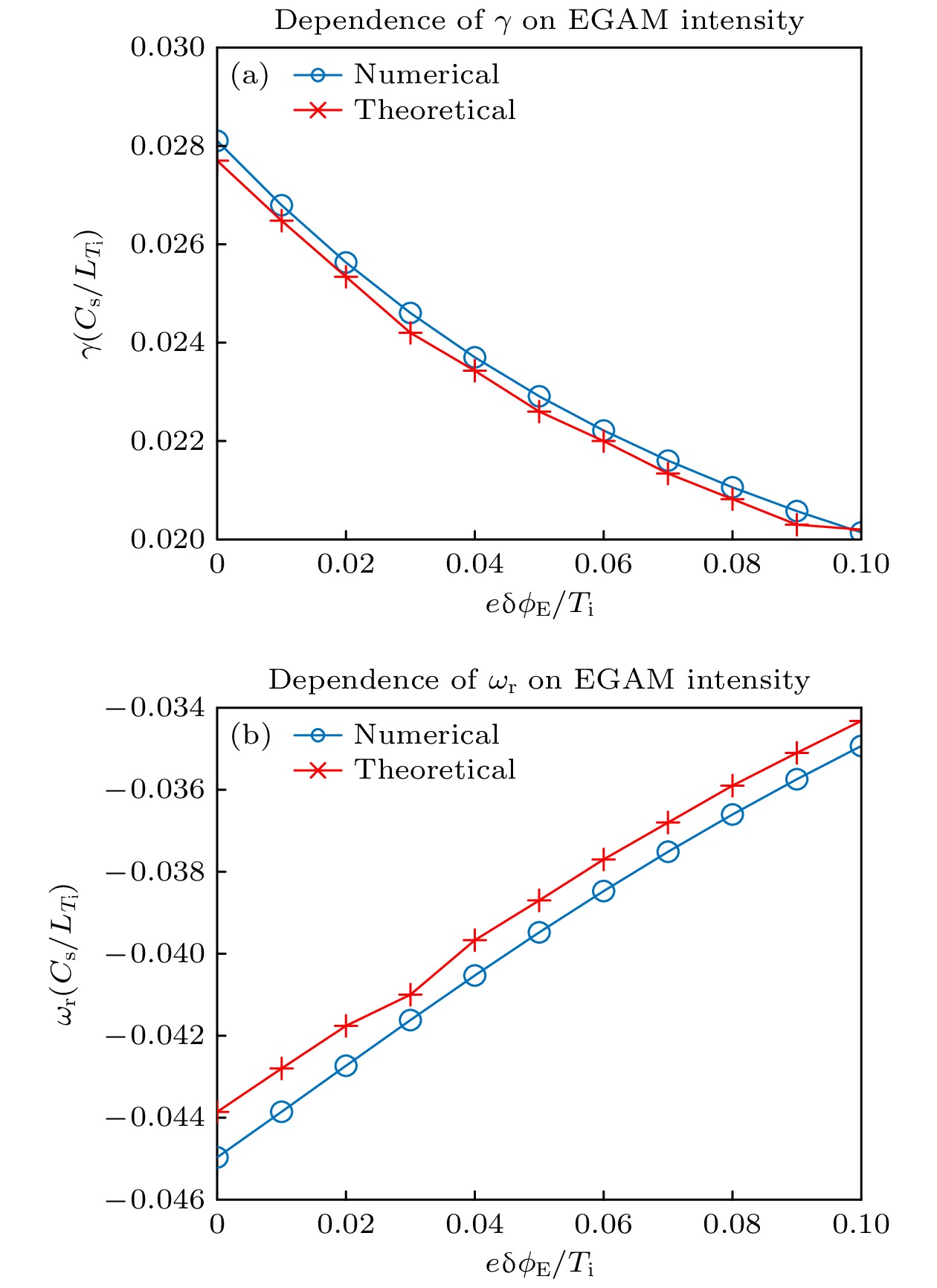
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}}=0 $ and$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}}=0.1 $ , respectively.
图 3 短波长极限下, ITG的增长率 (a)和实频(b)与EGAM幅度
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}} $ 的关系. 蓝色圆点表示直接数值求解本征值方程(9)得到的数值解, 红色叉号表示求解基态色散关系(14)得到的理论解. 实频和增长率都是用$ C_{\rm s}/L_{T_{\rm i}} $ 进行归一化, 其中,$ C_{\rm s}^2=2 T_{\rm e}/m_{\rm i} $ 表示声速; 这两幅图所用的参数为$ \varepsilon_ {T_{\rm i}}= $ $ 0.2 $ ,$ b=1 $ Fig. 3. Dependence of the growth rate (a) and real frequency (b) of ITG on the amplitude of EGAM
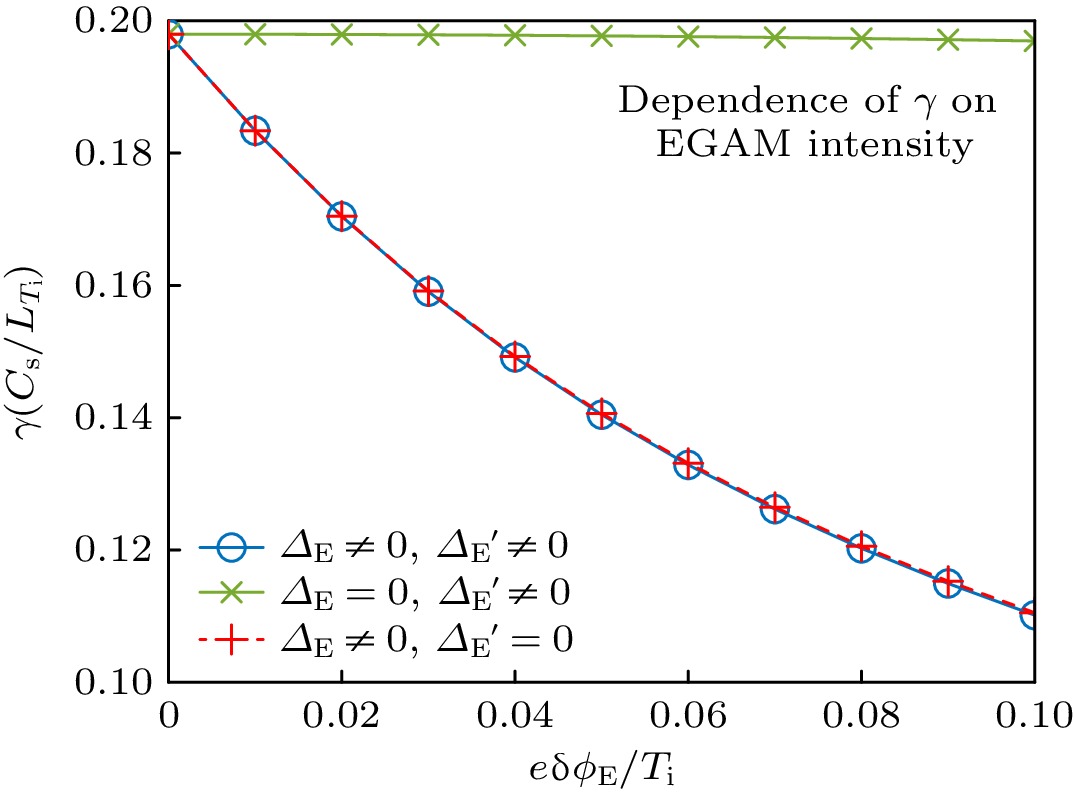
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}} $ in short-wavelength limit. The blue circles represent the numerical value obtained by directly solving the eigenmode equation (9); while the red crosses represent the theoretical value obtained by solving the dispersion relation (14). The real frequency and growth rate of ITG are normalized to$ C_{\rm s}/L_{T_{\rm i}} $ , with$ C_{\rm s}^2=2 T_{\rm e}/m_{\rm i} $ representing sound velocity. The parameters used here are$ \varepsilon_ {T_{\rm i}}=0.2 $ and$ b=1 $ .
图 4 短波长极限下, 极向旋转和密度调制共同作用和分别作用时 ITG 增长率对 EGAM 幅度的依赖关系. 图中绿色实线表示只有密度扰动的情形, 红色虚线表示只有电势扰动的情形, 蓝色实线表示两种扰动都存在的情形
Fig. 4. Dependence of the growth rate of ITG in presence of poloidal rotation and/or density modulation in short-wavelength limit. The green solid and red dashed lines represent the cases with only density modulation and poloidal rotation, respectively; while the blue line represents the case with both effects.
图 5 长波长极限下,
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}} = 0 $ (a)和$ 0.1 $ (b)时, ITG的本征值分布. 在两种情况下, 最不稳定的都是l = 0的基态Fig. 5. Distribution of eigenvalues of ITG when
$ e{{\text{δ}}}\phi_ {{\rm E}}/T_{{\rm i}} = 0 $ (a) and$ 0.1 $ (b) in the long-wavelength limit. In both cases, the ground state with l = 0 is the most unstable eigenstate.
图 6 长波长极限下,
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}}=0.1 $ 和0时, ITG最不稳定的基态的平行模结构. 其中, 蓝色实线表示径向电场为零时ITG的模结构, 红色虚线表示有限径向电场时ITG的模结构Fig. 6. Mode structure of the most unstable mode of ITG. The blue solid and red dashed lines represent the cases with
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}}=0 $ and$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}}=0.1 $ , respectively.
图 7 长波长极限下, ITG的增长率 (a)和实频(b)与EGAM幅度
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}} $ 的关系. 蓝色圆点表示直接数值求解本征值方程(9) 得到的数值解, 红色叉号表示求解基态色散关系(19)得到的理论解. 这两幅图所用的参数为$ \varepsilon_ {T_{\rm i}}=0.2 $ , b = 0.01Fig. 7. Dependence of the growth rate (a) and real frequency (b) of ITG on the amplitude of EGAM
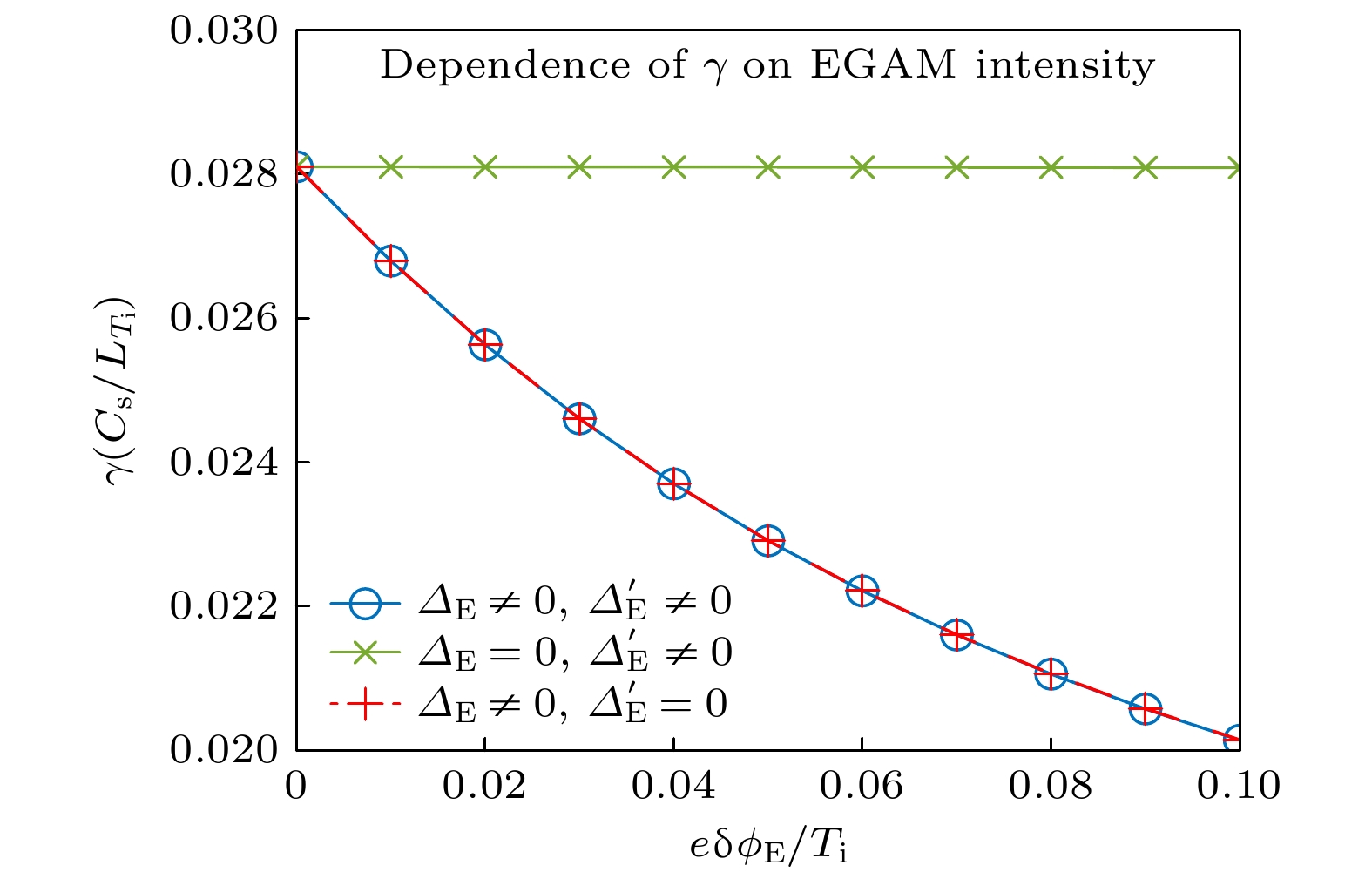
$ e{{\text{δ}}}\phi_{{\rm E}}/T_{{\rm i}} $ in long-wavelength limit. The blue circles represent the numerical value obtained by directly solving the eigenmode equation (9); while the red crosses represent the theoretical value obtained by solving the dispersion relation (19). The parameters used here are$ \varepsilon_ {T_{\rm i}}=0.2 $ and b = 0.01.
图 8 长波长极限下, 极向旋转和密度调制共同作用和分别作用时 ITG 增长率对 EGAM 幅度的依赖关系. 图中绿色实线表示只有密度扰动的情形, 红色虚线表示只有电势扰动的情形, 蓝色实线表示两种扰动都存在的情形
Fig. 8. Dependence of the growth rate of ITG in presence of poloidal rotation and/or density modulation in long-wavelength limit. The green solid and red dashed lines represent the cases with only density modulation and poloidal rotation, respectively; while the blue line represents the case with both effects.
-
[1] Horton W 1999 Rev. Mod. Phys. 71 735
Google Scholar
[2] Lin Z H, Hahm T S, Lee W W, Tang W, White R 1998 Science 281 1835
Google Scholar
[3] Hahm T S, Beer M, Lin Z H, Hammett G, Lee W W, Tang W 1999 Phys. Plasmas 6 922
Google Scholar
[4] Chen L, Lin Z H, White R 2000 Phys. Plasmas 7 3129
Google Scholar
[5] Zonca F, Chen L 2008 Europhys. Lett. 83 35001
Google Scholar
[6] Nazikian R, Fu G Y, Austin M, Berk H, Budny R, Gorelenkov N, Heidbrink W, Holcomb C, Kramer G, McKee G, Makowski M, Solomon W, Shafer M, Strait E, Van Zeeland M 2008 Phys. Rev. Lett. 101 185001
Google Scholar
[7] Fu G Y 2008 Phys. Rev. Lett. 101 185002
Google Scholar
[8] Qiu Z Y, Zonca F, Chen L 2010 Plasma Phys. Control. Fusion 52 095003
Google Scholar
[9] Berk H, Zhou T 2010 Nuclear Fusion 50 035007
Google Scholar
[10] Qiu Z Y, Chen L, Zonca F, Chen W 2018 Phys. Rev. Lett. 120 135001
Google Scholar
[11] Zarzoso D, Sarazin Y, Garbet X, Dumont R, Strugarek A, Abiteboul J, Cartier-Michaud T, Dif-Pradalier G, Ghendrih P, Grandgirard V, Latu G, Passeron C, Thomine O 2013 Phys. Rev. Lett. 110 125002
Google Scholar
[12] Dimits A, Bateman G, Beer M, Cohen B, Dorland W, Hammett G, Kim C, Kinsey J, Kotschenreuther M, Kritz A, Lao L L, Mandrekas J, Nevins W, Parker S, Redd A, Shumaker D, Sydora R, Weiland J 2000 Phys. Plasmas 7 969
Google Scholar
[13] Qiu Z Y, Chen L, Zonca F 2014 Phys. Plasmas 21 022304
Google Scholar
[14] Qiu Z Y, Chen L, Zonca F 2015 Phys. Plasmas 22 042512
Google Scholar
[15] Tardini G, Hobirk J, Igochine V, Maggi C, Martin P, McCune D, Peeters A, Sips A, Stäbler A, Stober J, the ASDEX Upgrade Team 2007 Nuclear Fusion 47 280
Google Scholar
[16] Mantica P, Strintzi D, Tala T, Giroud C, Johnson T, Leggate H, Lerche E, Loarer T, Peeters A, Salmi A, Sharapov S, Van Eester D, de Vries P, Zabeo L, Zastrow K 2009 Phys. Rev. Lett. 102 175002
Google Scholar
[17] Romanelli M, Zocco A, Crisanti F, JET-EFDA Contributors 2010 Plasma Phys. Control. Fusion 52 045007
Google Scholar
[18] Garcia J, Challis C, Citrin J, Doerk H, Giruzzi G, Görler T, Jenko F, Maget P. JET Contributors 2015 Nuclear Fusion 55 053007
Google Scholar
[19] Citrin J, Jenko F, Mantica P, Told D, Bourdelle C, Garcia J, Haverkort J, Hogeweij G, Johnson T, Pueschel M 2013 Phys. Rev. Lett. 11 1
Google Scholar
[20] Chankin A, McCracken G 1993 Nuclear Fusion 33 1459
Google Scholar
[21] Cheng C Z, Chen L, Chance M 1985 Ann. Phys. 161 21
Google Scholar
[22] Chen L 1994 Phys. Plasmas 1 1519
Google Scholar
[23] Qiu Z Y, Chen L, Zonca F 2016 Nuclear Fusion 56 106013
Google Scholar
[24] Qiu Z Y, Chen L, Zonca F 2017 Nuclear Fusion 57 056017
Google Scholar
[25] Chen L, Qiu Z Y, Zonca F 2022 Nuclear Fusion 62 094001
Google Scholar
[26] Chen L, Qiu Z Y, Zonca F 2014 Europhys. Lett. 107 15003
Google Scholar
[27] Romanelli F, Zonca F 1993 Phys. Fluids B 5 4081
Google Scholar
[28] Chen L, Briguglio S, Romanelli F 1991 Phys. Fluids B 3 611
Google Scholar
[29] Chen N F, Hu H Y, Zhang X Y, Wei S Z, Qiu Z Y 2021 Phys. Plasmas 28 042505
Google Scholar
下载:
计量
- 文章访问数: 2427
- PDF下载量: 74
- 被引次数: 0
