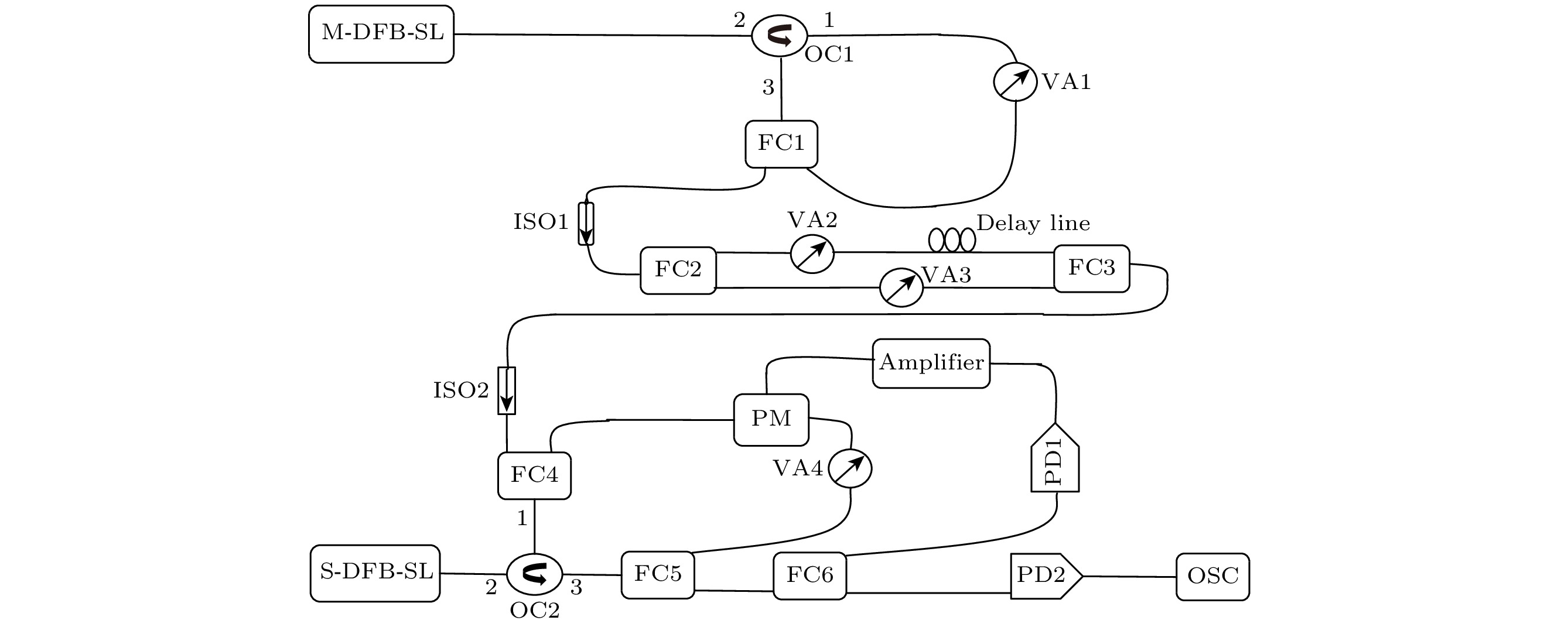
-
Distributed feedback semiconductor lasers (DFB-SLs) are the class B lasers, and would output chaotic laser under the external disturbances, such as external optical feedback and optical injection. Chaotic laser are widely used in many fields, including optical fiber sensing, chaotic laser secure communication, and better entropy sources for generating high-speed random number. However, the chaotic laser outputted from the semiconductor lasers with external cavity optical feedback produces a time delay signature (TDS) , which limits the applications of chaotic laser. On the other hand, the bandwidth (BW) of chaotic carrier signal plays the important role in determining the transmission rate of information signal. Therefore, the TDS and BW are two important parameters that will affect chaotic laser’s applications, and they are usually used to describe the chaos characteristics of chaotic laser. In this paper, we present a new scheme used to describe the TDS and investigate the BW of chaotic laser from semiconductor laser. For this scheme, the output laser from a DFB-SL with external single optical feedback is injected in double ways into another DFB-SL with phase modulation optical feedback by self chaos light. Thus they form a semiconductor laser system with external double optical injection and phase modulation optical feedback by self chaos light (SL-EDOI-PMOFBSCL). We investigate numerically the influences of the system parameters on TDS, such as the injection coefficient and feedback coefficient. Then the suppression effects on TDS are contrasted and analyzed with two other systems, that is to say, the semiconductor laser with external double optical injection and optical feedback (SL-EDOI-OF) and the semiconductor laser with external single optical injection and phase modulation optical feedback by self chaos light (SL-ESOI-PMOFBSCL). The results indicate that the proposed scheme in this work has the better suppression effect on TDS. Then the BW of the chaotic laser is investigated under the parameters conditions of effectively suppressing TDS. The simulation results show that the scheme proposed in this work can enhance the BW of chaotic laser by appropriately selecting the parametric values, and the maximum BW value of the obtained chaotic laser reaches about 16 GHz. -
Keywords:
- distributed feedback semiconductor laser /
- phase modulation optical feedback by self chaos light /
- time delay signature /
- bandwidth
[1] Wang Y, Wang B, Wang A 2008 IEEE Photonics. Technol. Lett. 20 1636
Google Scholar
[2] 王宇, 靳宝全, 张建国, 王东, 张明江, 王安帮, 王云才 2018 光学学报 38 0328016
Google Scholar
Wang Y, Jin B Q, Zhang J G, Wang D, Zhang M J, Wang A B, Wang Y C 2018 Acta Opt. Sin. 38 0328016
Google Scholar
[3] Simpson T B, Liu J M, Gavrielides A, Kovanis V, Alsing P M 1995 Phys. Rev. A 51 4181
Google Scholar
[4] Lin F Y, Liu J M 2003 Opt. Commun. 221 173
Google Scholar
[5] Senlin Y 2009 J. Opt. Commun. 30 20
Google Scholar
[6] Deng T, Xia G Q, Cao L P, Chen J G, Lin X D, Wu Z M 2009 Opt. Commun. 282 2243
Google Scholar
[7] Argyris A, Syvridis D, Larger L, Annovazzi V 2005 Nature 438 343
Google Scholar
[8] Uchida A, Amano K, Inoue M, Hirano K, Naito S, Someya H, Yoshimura K 2008 Nat. Photonics. 2 728
Google Scholar
[9] Metropolis N, Ulam S 1949 J. Am. Stat. Assoc. 44 335
Google Scholar
[10] 张继兵, 张建忠, 杨毅彪, 梁君生, 王云才 2010 59 7679
Google Scholar
Zhang J B, Zhang J Z, Yang Y B, Liang J S, Wang Y C 2010 Acta Phys. Sin. 59 7679
Google Scholar
[11] Wu J G, Xia G Q, Tang X, Lin X D, Wu Z M 2010 Opt. Express. 18 6661
Google Scholar
[12] Jafari A, Sedghi H, Mabhouti K, Behnia S 2011 Opt. Commun. 284 3018
Google Scholar
[13] Udaltsov V S, Goedgebuer J P, Larger L, Vladimir S, Cuenot J, William T, Rhodes 2003 Phys. Lett. E 308 54
Google Scholar
[14] Rontani D, Locquet A, Sciamanna M, Citrin D S 2007 Opt. Lett. 32 2960
Google Scholar
[15] Vicente R, Daudén J, Colet P, Toral R 2005 IEEE J. Quantum Electron. 41 541
Google Scholar
[16] Xiang S, Pan W, Zhang L 2014 Opt. Commun. 324 38
Google Scholar
[17] 贾耕涛, 陈毅龙, 余江涛, 柯俊翔, 义理林 2018 光通信研究 2 11
Google Scholar
Jia G T, Chen Y L, Yu J T, Ke J X, Yi L L 2018 Study Opt. Commun. 2 11
Google Scholar
[18] 张晓旭, 吴天安, 常凯歌, 张胜海 2017 中国激光 44 0501010
Google Scholar
Zhang X X, Wu T A, Chang K G, Zhang S H 2017 Chin. J. Lasers. 44 0501010
Google Scholar
[19] Lin F Y, Liu J M 2004 IEEE J. Quantum Electron. 40 815
Google Scholar
[20] Wang Y, Zhang G, Wang A 2007 Opt. Commun. 277 156
Google Scholar
[21] 颜森林 2019 中国激光 46 0808003
Google Scholar
Yan S L 2019 Chin. J. Lasers. 46 0808003
Google Scholar
[22] Wang A, Yang Y, Wang B, Zhang B, Li L, Wang Y C 2013 Opt. Express 21 8701
Google Scholar
[23] Zhao A, Jiang N, Liu S, Xue C P, Tang J M, Qiu K 2019 Opt. Express 27 12336
Google Scholar
[24] 孙巍阳, 胡宝洁, 王航 2019 激光与光电子学进展 56 211404
Google Scholar
Sun W Y, Hu B J, Wang H 2019 Las. Optoelect. Prog. 56 211404
Google Scholar
[25] Cui S, Zhang J Z 2019 IEEE Photonics J. 11 7905208
Google Scholar
[26] Zhang R, Zhou P, Yang Y G, Fang Q, Mu P H 2020 Opt. Express. 28 7197
Google Scholar
[27] 李增, 冯玉玲, 王晓茜, 姚治海 2018 67 140501
Google Scholar
Li Z, Feng Y L, Wang X Q, Yao Z H 2018 Acta Phys. Sin. 67 140501
Google Scholar
[28] 张依宁, 冯玉玲, 王晓茜, 赵振明, 高超, 姚治海 2020 69 090501
Google Scholar
Zhang Y N, Feng Y L, Wang X Q, Zhao Z M, Gao C, Yao Z H 2020 Acta Phys. Sin. 69 090501
Google Scholar
[29] Lang R, Kobayashi K 1980 IEEE J. Quantum Electron. 16 347
Google Scholar
[30] 卢东, 钟祝强, 夏光琼, 吴正茂 2016 光子学报 45 1014003
Google Scholar
Lu D, Zhong Z Q, Xia G Q, Wu Z M 2016 Acta Photon. Sin. 45 1014003
Google Scholar
[31] Mikami T, Kanno K, Aoyama K 2012 Phys. Rev. E 85 016211
Google Scholar
[32] 王云才, 张耕玮, 王安帮, 王冰洁, 李艳丽, 郭萍 2007 56 4372
Google Scholar
Wang Y C, Zhang G W, Wang A B, Wang B J, Li Y L, Guo P 2007 Acta Phys. Sin. 56 4372
Google Scholar
[33] 阎娟, 潘炜, 李念强, 张力月, 刘庆喜 2016 65 204203
Google Scholar
Yan J, Pan W, Li N Q, Zhang L Y, Liu Q X 2016 Acta Phys. Sin. 65 204203
Google Scholar
[34] 王永胜, 赵彤, 王安帮, 张明江, 王云才 2017 激光与光电子进展 54 111401
Google Scholar
Wang Y S, Zhao T, Wang A B, Zhang M J, Wang Y C 2017 Las. Optoelect. Prog. 54 111401
Google Scholar
-
图 1 具有外光双路注入的自混沌光相位调制的光反馈半导体激光器系统的示意图
Figure 1. Schematic diagram of semiconductor laser system with external double optical injection and phase modulation optical feedback by self chaos light.
图 2 SL-EDOI-PMOFBSCL在延迟时间
$ {\tau _{\text{s}}} = 3 $ ns下输出混沌激光的(a)时间序列和(b)对应的自相关函数曲线Figure 2. Time series (a) and the corresponding ACF curves (b) of chaotic laser from the SL-EDOI-PMOFBSCL at times delay
$ {\tau _{\text{s}}} = 3 $ ns.
图 3 SL-EDOI-PMOFBSCL输出混沌光延时特征值
$ \beta $ 随参数$ {K_{\text{s}}} $ 和$ {K_{\text{m}}} $ 变化的二维图Figure 3. Two-dimensional maps of the time-delay characteristic value
$ \beta $ in the parameter space of$ {K_{\text{s}}} $ and$ {K_{\text{m}}} $ for chaotic laser from the SL-EDOI-PMOFBSCL.
图 4 SL-EDOI-PMOFBSCL输出混沌激的延时特征值
$ \beta $ 随参数$ {K_{\text{1}}} $ 和$ {K_{\text{2}}} $ 变化的二维图Figure 4. Two-dimensional maps of the time-delay characteristic value
$ \beta $ in the parameter space of$ {K_{\text{1}}} $ and$ {K_{\text{2}}} $ for chaotic laser from the SL-EDOI-PMOFBSCL.
图 5 SL-EDOI-PMOFBSCL输出混沌光的延时特征值
$ \beta $ 随参数$ {K_{\text{s}}} $ 和$ {K_{\text{2}}} $ 变化的二维图Figure 5. Two-dimensional maps of the time-delay characteristic value
$ \beta $ in the parameter space of$ {K_{\text{s}}} $ and$ {K_{\text{2}}} $ for chaotic laser from the SL-EDOI-PMOFBSCL.
图 6 SL-EDOI-PMOFBSCL输出混沌光的延时特征值
$ \beta $ 随$ {P_{\text{m}}} $ 的变化曲线Figure 6. Curve of the time delay characteristic values
$ \beta $ with$ {P_{\text{m}}} $ for chaotic laser from the SL-EDOI-PMOFBSCL.
图 7 SL-EDOI-PMOFBSCL输出混沌激光的延时特征值
$ \beta $ 随$ \Delta f $ 的变化曲线Figure 7. Curve of the time delay characteristic values
$ \beta $ versus$ \Delta f $ for chaotic laser from the SL-EDOI-PMOFBSCL.
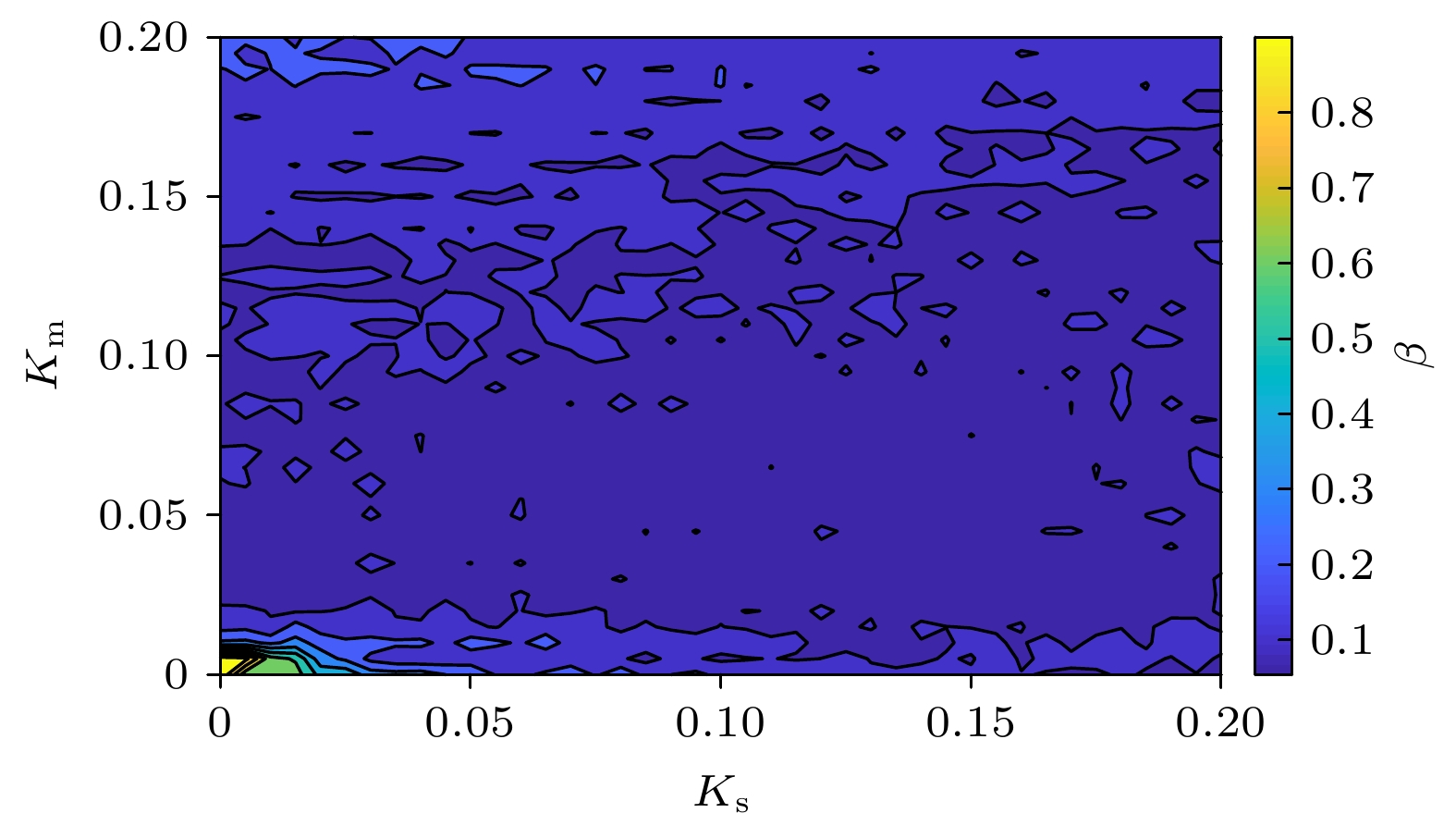
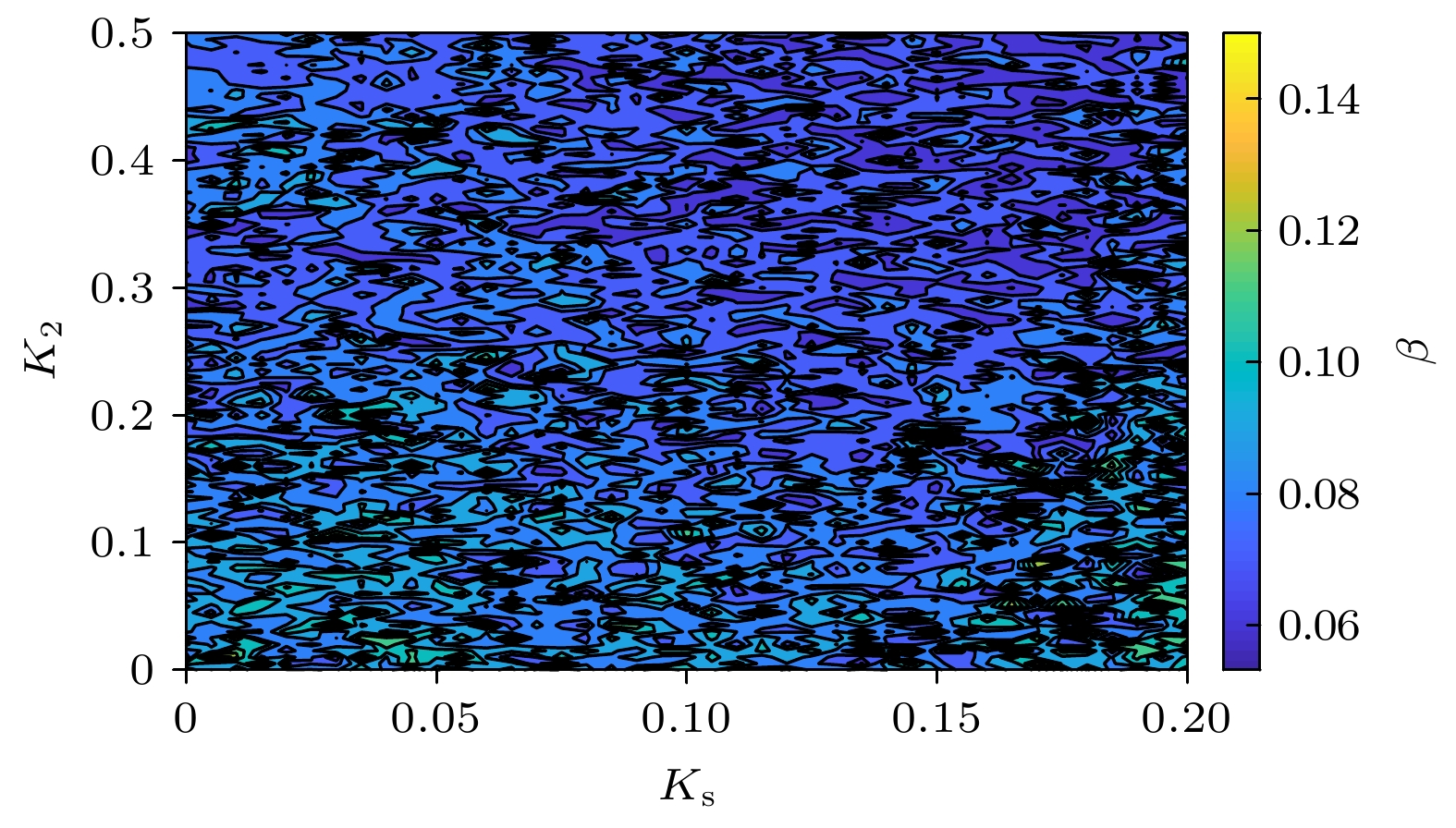
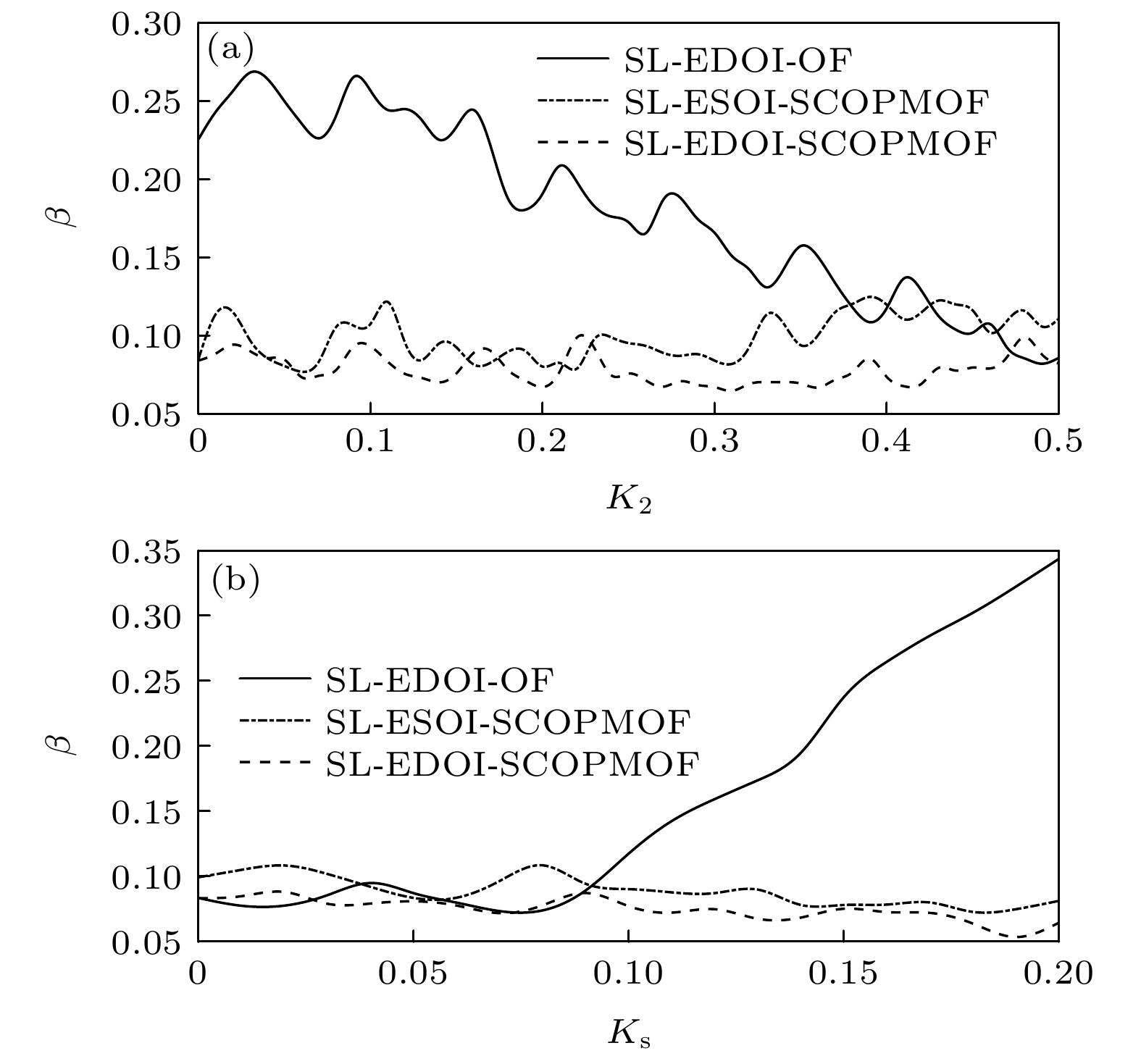
图 8 对于SL-EDOI-OF和SL-ESOI-PMOFBSCL以及SL-EDOI-PMOFBSCL 输出的混沌光(a)延时特征值
$ \beta $ 随$ {K_{\text{2}}} $ 和(b)$ {K_{\text{s}}} $ 的变化曲线Figure 8. Curves of the time delay characteristic value
$ \beta $ versus (a)$ {K_{\text{2}}} $ and (b)$ {K_{\text{s}}} $ for chaotic laser from the SL-EDOI-OF, SL-ESOI-PMOFBSCL and SL-EDOI-PMOFBSCL
图 9 SL-EDOI-PMOFBSCL在反馈系数
$ {K_{\text{m}}} $ = 0.06下输出混沌激光的(a)时间序列和(b)对应的功率谱. 其中(b)中的虚线标示了混沌光的3 dB带宽值Figure 9. Time series (a) and the corresponding power spectra (b) for chaotic laser from SL-EDOI-PMOFBSCL at feedback factor
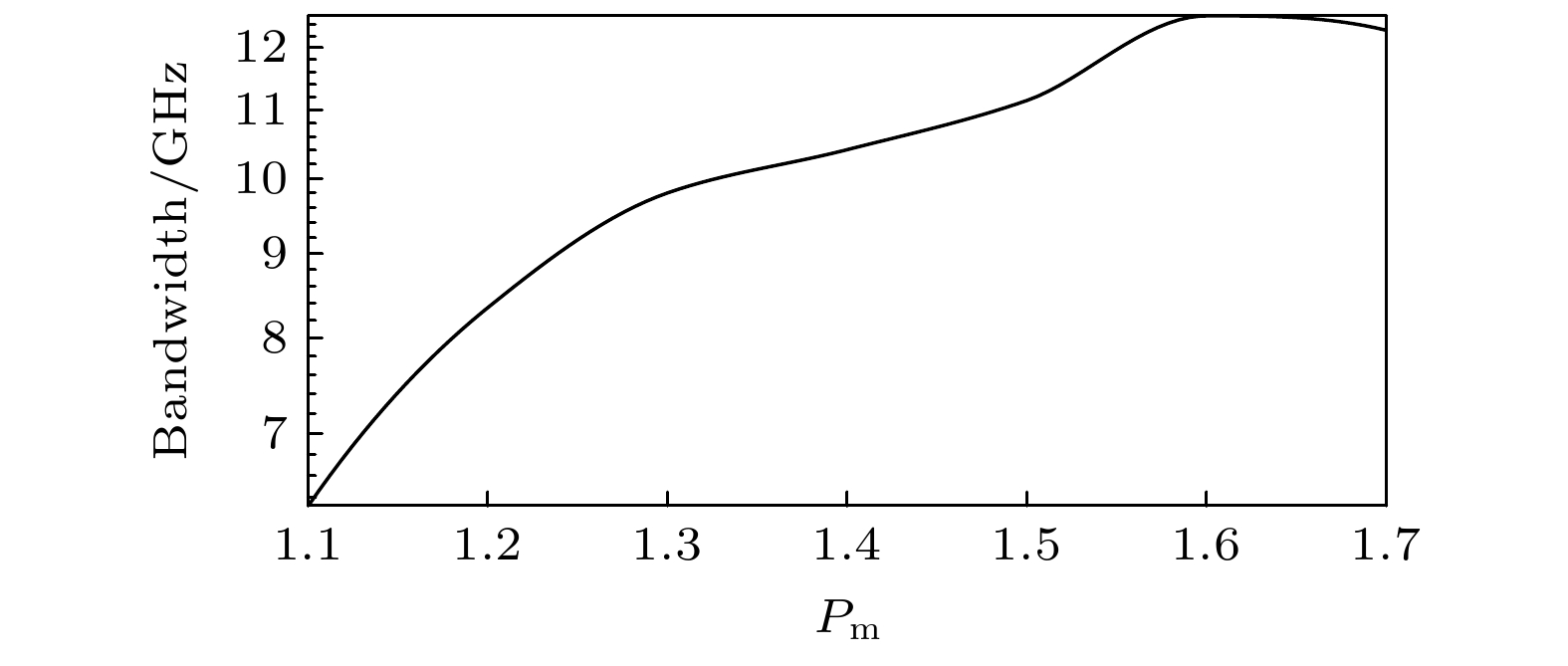
$ {K_{\text{m}}} $ = 0.06, the dashed lines in (b) indicate the value of the 3 dB bandwidth of the chaotic laser.
图 10 SL-EDOI-PMOFBSCL输出混沌激光带宽随反馈系数
$ {K_{\text{m}}} $ 的变化曲线Figure 10. Curve of bandwidth versus feedback coefficient
$ {K_{\text{m}}} $ for chaotic laser from SL-EDOI-PMOFBSCL.
图 11 在不同
$ {K_{\text{m}}} $ 值下SL-EDOI-PMOFBSCL输出混沌光带宽随反馈系数$ {K_{\text{s}}} $ 变化曲线 (a)$ {K_{\text{m}}} $ = 0.12; (b)$ {K_{\text{m}}} $ = 0.18Figure 11. Curves of bandwidth versus feedback coefficient
$ {K_{\text{s}}} $ for chaotic laser from the SL-EDOI-PMOFBSCL at different Km: (a)$ {K_{\text{m}}} $ = 0.12; (b)$ {K_{\text{m}}} $ = 0.18.
图 12 SL-EDOI-PMOFBSCL输出混沌激光的带宽随
$ {K_{\text{2}}} $ 的变化曲线Figure 12. Bandwidth versus
$ {K_{\text{2}}} $ for chaotic laser from the SL-EDOI-PMOFBSCL.
图 13 SL-EDOI-PMOFBSCL输出混沌激光的带宽随
$ {P_{\text{m}}} $ 的变化Figure 13. Bandwidth versus
$ {P_{\text{m}}} $ for chaotic laser from the SL-EDOI-PMOFBSCL.
图 14 SL-EDOI-PMOFBSCL输出混沌激光带宽随
$ \Delta f $ 的变化Figure 14. Bandwidth versus
$ \Delta f $ for chaotic laser from the SL-EDOI-PMOFBSCL. -
[1] Wang Y, Wang B, Wang A 2008 IEEE Photonics. Technol. Lett. 20 1636
Google Scholar
[2] 王宇, 靳宝全, 张建国, 王东, 张明江, 王安帮, 王云才 2018 光学学报 38 0328016
Google Scholar
Wang Y, Jin B Q, Zhang J G, Wang D, Zhang M J, Wang A B, Wang Y C 2018 Acta Opt. Sin. 38 0328016
Google Scholar
[3] Simpson T B, Liu J M, Gavrielides A, Kovanis V, Alsing P M 1995 Phys. Rev. A 51 4181
Google Scholar
[4] Lin F Y, Liu J M 2003 Opt. Commun. 221 173
Google Scholar
[5] Senlin Y 2009 J. Opt. Commun. 30 20
Google Scholar
[6] Deng T, Xia G Q, Cao L P, Chen J G, Lin X D, Wu Z M 2009 Opt. Commun. 282 2243
Google Scholar
[7] Argyris A, Syvridis D, Larger L, Annovazzi V 2005 Nature 438 343
Google Scholar
[8] Uchida A, Amano K, Inoue M, Hirano K, Naito S, Someya H, Yoshimura K 2008 Nat. Photonics. 2 728
Google Scholar
[9] Metropolis N, Ulam S 1949 J. Am. Stat. Assoc. 44 335
Google Scholar
[10] 张继兵, 张建忠, 杨毅彪, 梁君生, 王云才 2010 59 7679
Google Scholar
Zhang J B, Zhang J Z, Yang Y B, Liang J S, Wang Y C 2010 Acta Phys. Sin. 59 7679
Google Scholar
[11] Wu J G, Xia G Q, Tang X, Lin X D, Wu Z M 2010 Opt. Express. 18 6661
Google Scholar
[12] Jafari A, Sedghi H, Mabhouti K, Behnia S 2011 Opt. Commun. 284 3018
Google Scholar
[13] Udaltsov V S, Goedgebuer J P, Larger L, Vladimir S, Cuenot J, William T, Rhodes 2003 Phys. Lett. E 308 54
Google Scholar
[14] Rontani D, Locquet A, Sciamanna M, Citrin D S 2007 Opt. Lett. 32 2960
Google Scholar
[15] Vicente R, Daudén J, Colet P, Toral R 2005 IEEE J. Quantum Electron. 41 541
Google Scholar
[16] Xiang S, Pan W, Zhang L 2014 Opt. Commun. 324 38
Google Scholar
[17] 贾耕涛, 陈毅龙, 余江涛, 柯俊翔, 义理林 2018 光通信研究 2 11
Google Scholar
Jia G T, Chen Y L, Yu J T, Ke J X, Yi L L 2018 Study Opt. Commun. 2 11
Google Scholar
[18] 张晓旭, 吴天安, 常凯歌, 张胜海 2017 中国激光 44 0501010
Google Scholar
Zhang X X, Wu T A, Chang K G, Zhang S H 2017 Chin. J. Lasers. 44 0501010
Google Scholar
[19] Lin F Y, Liu J M 2004 IEEE J. Quantum Electron. 40 815
Google Scholar
[20] Wang Y, Zhang G, Wang A 2007 Opt. Commun. 277 156
Google Scholar
[21] 颜森林 2019 中国激光 46 0808003
Google Scholar
Yan S L 2019 Chin. J. Lasers. 46 0808003
Google Scholar
[22] Wang A, Yang Y, Wang B, Zhang B, Li L, Wang Y C 2013 Opt. Express 21 8701
Google Scholar
[23] Zhao A, Jiang N, Liu S, Xue C P, Tang J M, Qiu K 2019 Opt. Express 27 12336
Google Scholar
[24] 孙巍阳, 胡宝洁, 王航 2019 激光与光电子学进展 56 211404
Google Scholar
Sun W Y, Hu B J, Wang H 2019 Las. Optoelect. Prog. 56 211404
Google Scholar
[25] Cui S, Zhang J Z 2019 IEEE Photonics J. 11 7905208
Google Scholar
[26] Zhang R, Zhou P, Yang Y G, Fang Q, Mu P H 2020 Opt. Express. 28 7197
Google Scholar
[27] 李增, 冯玉玲, 王晓茜, 姚治海 2018 67 140501
Google Scholar
Li Z, Feng Y L, Wang X Q, Yao Z H 2018 Acta Phys. Sin. 67 140501
Google Scholar
[28] 张依宁, 冯玉玲, 王晓茜, 赵振明, 高超, 姚治海 2020 69 090501
Google Scholar
Zhang Y N, Feng Y L, Wang X Q, Zhao Z M, Gao C, Yao Z H 2020 Acta Phys. Sin. 69 090501
Google Scholar
[29] Lang R, Kobayashi K 1980 IEEE J. Quantum Electron. 16 347
Google Scholar
[30] 卢东, 钟祝强, 夏光琼, 吴正茂 2016 光子学报 45 1014003
Google Scholar
Lu D, Zhong Z Q, Xia G Q, Wu Z M 2016 Acta Photon. Sin. 45 1014003
Google Scholar
[31] Mikami T, Kanno K, Aoyama K 2012 Phys. Rev. E 85 016211
Google Scholar
[32] 王云才, 张耕玮, 王安帮, 王冰洁, 李艳丽, 郭萍 2007 56 4372
Google Scholar
Wang Y C, Zhang G W, Wang A B, Wang B J, Li Y L, Guo P 2007 Acta Phys. Sin. 56 4372
Google Scholar
[33] 阎娟, 潘炜, 李念强, 张力月, 刘庆喜 2016 65 204203
Google Scholar
Yan J, Pan W, Li N Q, Zhang L Y, Liu Q X 2016 Acta Phys. Sin. 65 204203
Google Scholar
[34] 王永胜, 赵彤, 王安帮, 张明江, 王云才 2017 激光与光电子进展 54 111401
Google Scholar
Wang Y S, Zhao T, Wang A B, Zhang M J, Wang Y C 2017 Las. Optoelect. Prog. 54 111401
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4536
- PDF Downloads: 104
- Cited By: 0
