-
The beam splitter is an optical element that divides a beam of light into two or more subbeams. It is an essential component in many optical experiments. X-ray has the characteristics of short wavelength and strong penetration ability, making it hard to use the optical elements in the visible-light region. Therefore, it is necessary to develop optical elements suitable for X-rays. The atomic layer spacing of the perfect crystal is of the same order of magnitude as the X-ray wavelength, so the crystal diffraction effect can be used to achieve the X-ray modulation. In this paper, the beam splitting characteristics of Laue crystal are analyzed based on X-ray diffraction dynamics and the influences of crystal absorption and incident light angular divergence on the rocking curves of transmission and diffraction are simulated. The modulation of the crystal diffraction in-plane angle and crystal thickness to Laue diffraction beam-splitting ratio is presented quantitatively. The results show that the kinematical theory of X-ray diffraction is not enough to analyze the beam splitting characteristics of the crystal. It is necessary to consider the interaction between the wave fields in the crystal and use the Pendellӧsung effect in the dynamical theory of X-ray diffraction to explain the change of the crystal beam-splitting ratio quantitatively. The influence of angular divergence and crystal absorption are considered in the simulation. The angular divergence broadens the bandwidth of the diffraction, thereby reducing diffraction intensity. The crystal absorption results in asymmetry and peak shift of the transmission curve and affects the intensity of diffraction and the intensity of transmission beam. The experimental results show that the non-dispersive (+n, –n) configuration can effectively eliminate the influence of angle divergence. The beam-splitting ratio can be adjusted in a small range (±2%) by changing the in-plane angle and adjusted in a wide range (±75%) by changing the crystal thickness, thereby realizing the quantitative modulation of the intensity of transmission and diffraction beam.
-
Keywords:
- dynamical theory of X-ray diffraction /
- Laue diffraction /
- crystal beam splitter /
- synchrotron radiation
[1] 张克从 1998 近代晶体学基础(下册)(北京: 科学出版社) 第2−7页
Zhang K C 1998 Fundamentals of Modern Crystallography (Vol. 2) (Beijing: Science Press) pp2−7 (in Chinese)
[2] 徐朝银 2013 同步辐射光学与工程(合肥: 中国科学技术大学出版社) 第181−254页
Xu C Y 2013 Synchrotron Radiation Optics and Engineering (Hefei: Press of University of Science and Technology of China) pp181−254 (in Chinese)
[3] Xu H J, Zhao Z T 2008 Nucl. Sci. Tech 19 1
Google Scholar
[4] 邰仁忠 2021 物理 50 501
Google Scholar
Tai R Z 2021 Physics 50 501
Google Scholar
[5] Pelliccia D, Olbinado M P, Rack A, Kingston A M, Myers G R, Paganin D M 2018 IUCrJ 5 428
Google Scholar
[6] Kingston A M, Pelliccia D, Rack A, Olbinado M P, Cheng Y, Myers G R, Paganin D M 2018 Optica 5 1516
Google Scholar
[7] Villanueva-Perez P, Pedrini B, Mokso R, Vagovic P, Guzenko V A, Leake S J, Willmott P R, Oberta P, David C, Chapman H N, Stampanoni M 2018 Optica 5 1521
Google Scholar
[8] Schmidt K E, Spence J C H, Weierstall U, Kirian R, Wang X, Starodub D, Chapman H N, Howells M R, Doak R B 2008 Phys. Rev. Lett. 101 115507
Google Scholar
[9] Batterman B W, Cole H 1964 Rev. Modern Phys. 36 681
Google Scholar
[10] Bonse U, Hart M 1965 Appl. Phys. Lett. 6 155
Google Scholar
[11] Pelliccia D, Rack A, Scheel M, Cantelli V, Paganin D M 2016 Phys. Rev. Lett. 117 113902
Google Scholar
[12] Schori A, Shwartz S 2017 Opt. Express 25 14822
Google Scholar
[13] von Laue M, 1931 Ergeb. Exakt. Naturwiss 10 133
[14] Kato N, 1960 Acta Crystallography 13 349
Google Scholar
[15] Hirsch P B, 1952 Acta Crystallography 5 176
Google Scholar
[16] 麦振洪 2020 X射线衍射动力学: 理论与应用(北京: 科学出版社) 第10−49页
Mai Z H 2020 X-ray Diffraction Dynamics: Theory and Applications (Beijing: Science Press) pp10−49 (in Chinese)
[17] Zhao Z T, Xu H J 2004 Proceedings of European Particle Accelerator Conference Lucerne, Switzerland, June 5–9, 2004 p2368
[18] 杨俊亮, 李中亮, 李瑭, 朱晔, 宋丽, 薛莲, 张小威 2020 69 104101
Google Scholar
Yang J L, Li Z L, Li T, Zhu Y, Song L, Xue L, Zhang X W 2020 Acta Phys. Sin. 69 104101
Google Scholar
[19] Río M, Dejus R J 2011 Proc. Spie. 8141 259
[20] Zachariasen, W. H 1967 Phys. Rev. Lett. 18 195
Google Scholar
[21] del Rio M S, Perez-Bocanegra N, Shi X B, Honkimaki V, Zhang L 2015 J. Appl. Crystallogr. 48 477
Google Scholar
[22] Li Z L, Fan Y C, Xue L, Zhang Z Y, Wang J 2019 2019 AIP Conference Proceedings 2054 Taiwan, China, June 10−15, 2019 p060040
[23] Penning P, Polder D 1961 Philips Res. Rep. 16 419
-
图 1 透射率与反射率随偏移角
$\Delta \theta $ 的变化曲线(1 arcsec = 1/3600 degrees)Figure 1. Transmittance and reflectance curve with offset angle
$\Delta \theta $ (1 arcsec = 1/3600 degrees).
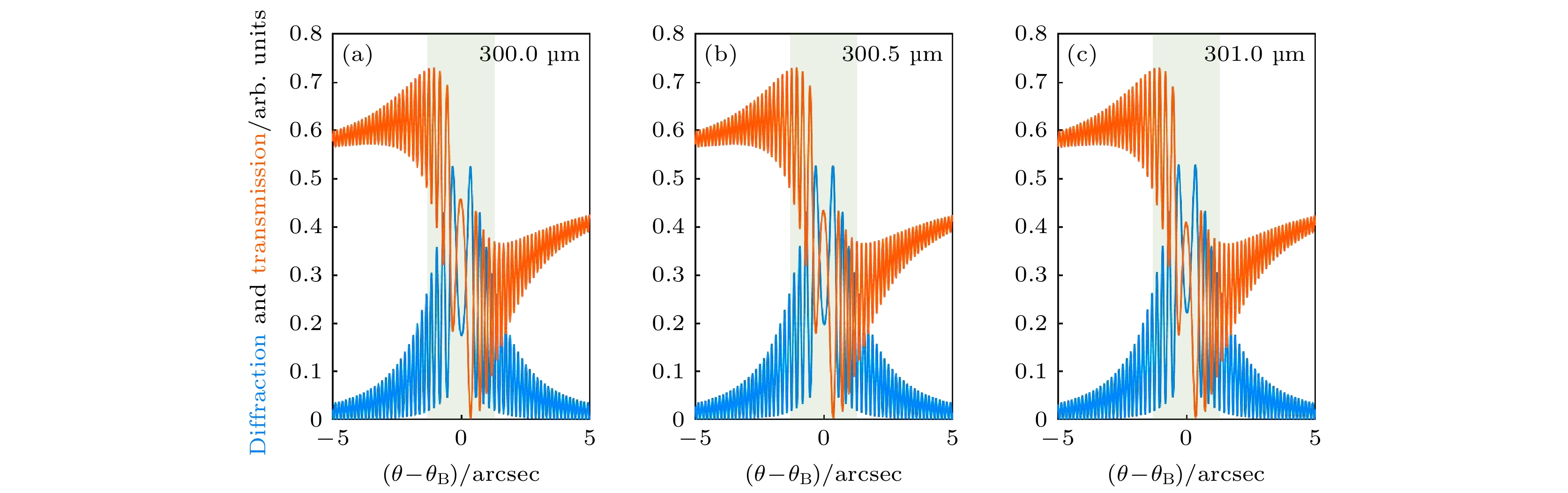
图 2 XOP模拟出的不同厚度Si单晶的摇摆曲线 Si单晶厚度分别为300 μm (a), 300.5 μm (b), 301 μm (c)的衍射和透射强度分布曲线, 没有经过强度平均的处理
Figure 2. The rocking curves of Si crystal with different thicknesses simulated by XOP: Diffraction and transmission intensity distribution curves of Si crystal with thickness of 300 μm (a), 300.5 μm (b), 301 μm (c), without intensity averaging.
图 3 XOP模拟出的不同厚度Si单晶的摇摆曲线 (a)—(c)Si单晶厚度分别为300 μm, 400 μm和500 μm的衍射和透射强度分布曲线, 经过2.6″角度窗口强度平均的处理; (d)—(f)与(a)—(b)对应, 为无吸收情况下的衍射和透射强度分布曲线, 经过2.6″角度窗口强度平均的处理
Figure 3. The rocking curves of Si crystal with different thicknesses simulated by XOP. (a)–(c) Diffraction and transmission intensity distribution curves of Si crystal with thickness of 300 μm, 400 μm and 500 μm, under 2.6″ angle window intensity averaging; (d)–(f) correspond to (a)–(c), which are the diffraction and transmission intensity distribution curves without absorption, which are processed by 2.6" angle window intensity averaging.
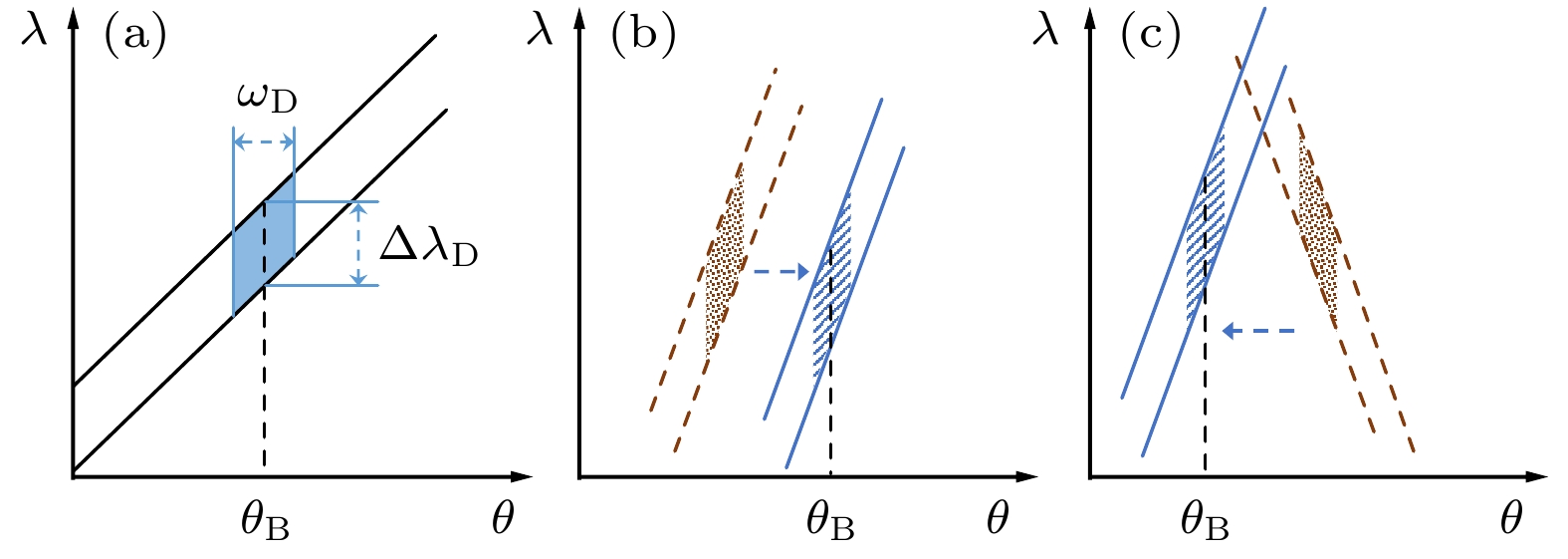
图 4 (a)完美晶体衍射的DuMond图; (b)消色散(+n, –n)配置条件下, 分束晶体扫描分析晶体出射光的DuMond图; (c)色散(+n, +n)配置条件下, 分束晶体扫描分析晶体出射光的DuMond图. 斜线区域是分析晶体的DuMond窗口, 散点区域是分束晶体的DuMond窗口
Figure 4. (a) DuMond diagram for perfect crystal diffraction; (b) DuMond diagrams during scanning the output beam of the analyzer by beam splitter with the non-dispersive (+n, –n) configuration; (c) DuMond diagrams during scanning the output beam of the analyzer by beam splitter with the dispersive (+n, +n) configuration. The oblique line region is the DuMond window of the analyzer and the point region is the DuMond window of the beam splitter.
图 5 分析晶体和分束晶体的消色散实验光路图
Figure 5. Experimental configuration of dispersive consists of analyzer and beam splitter.
图 6 晶体厚度为300 μm且
$\varphi = - {3^ \circ }$ 时的透射曲线与衍射曲线Figure 6. Transmission and diffraction curves when the crystal thickness is 300 μm and
$\varphi = - {3^ \circ }$ .
图 7 不同φ角下的透射曲线和衍射曲线
Figure 7. Transmission and diffraction curves at different φ.
图 8 (a)不同φ角下的强度分束比, 红线是数值拟合曲线; (b)不同φ角下的布拉格峰位置; (c)不同φ角下的摇摆曲线的峰值半高宽(FWHM), 其中红色虚线为晶体本征达尔文宽度
Figure 8. (a) Intensity splitting ratio (transmission intensity/diffraction intensity) at different φ, the red line is the linear fitting curve; (b) the peak positions of the diffraction curve at different φ; (c) the full width at half maximum (FWHM) of the rocking curve at different φ, where the red dashed line is the intrinsic Darwin Width of the crystal.
图 9 不同晶体厚度条件下的透射曲线和衍射曲线
Figure 9. Transmission curve and diffraction curve with different crystal thickness.
表 1 不同晶体厚度条件下得到的分束比、摇摆曲线半高宽测量值
Table 1. Beam splitting ratio, rocking curve FWHM measurement value obtained with different crystal thickness.
晶体厚度/
μm分束比(T/D) 摇摆曲线半高宽
测量值/arcsec本征达尔文带宽/
arcsec300 1.90 3.76 2.60 400 1.15 2.96 500 1.40 3.89 
DownLoad: CSV
-
[1] 张克从 1998 近代晶体学基础(下册)(北京: 科学出版社) 第2−7页
Zhang K C 1998 Fundamentals of Modern Crystallography (Vol. 2) (Beijing: Science Press) pp2−7 (in Chinese)
[2] 徐朝银 2013 同步辐射光学与工程(合肥: 中国科学技术大学出版社) 第181−254页
Xu C Y 2013 Synchrotron Radiation Optics and Engineering (Hefei: Press of University of Science and Technology of China) pp181−254 (in Chinese)
[3] Xu H J, Zhao Z T 2008 Nucl. Sci. Tech 19 1
Google Scholar
[4] 邰仁忠 2021 物理 50 501
Google Scholar
Tai R Z 2021 Physics 50 501
Google Scholar
[5] Pelliccia D, Olbinado M P, Rack A, Kingston A M, Myers G R, Paganin D M 2018 IUCrJ 5 428
Google Scholar
[6] Kingston A M, Pelliccia D, Rack A, Olbinado M P, Cheng Y, Myers G R, Paganin D M 2018 Optica 5 1516
Google Scholar
[7] Villanueva-Perez P, Pedrini B, Mokso R, Vagovic P, Guzenko V A, Leake S J, Willmott P R, Oberta P, David C, Chapman H N, Stampanoni M 2018 Optica 5 1521
Google Scholar
[8] Schmidt K E, Spence J C H, Weierstall U, Kirian R, Wang X, Starodub D, Chapman H N, Howells M R, Doak R B 2008 Phys. Rev. Lett. 101 115507
Google Scholar
[9] Batterman B W, Cole H 1964 Rev. Modern Phys. 36 681
Google Scholar
[10] Bonse U, Hart M 1965 Appl. Phys. Lett. 6 155
Google Scholar
[11] Pelliccia D, Rack A, Scheel M, Cantelli V, Paganin D M 2016 Phys. Rev. Lett. 117 113902
Google Scholar
[12] Schori A, Shwartz S 2017 Opt. Express 25 14822
Google Scholar
[13] von Laue M, 1931 Ergeb. Exakt. Naturwiss 10 133
[14] Kato N, 1960 Acta Crystallography 13 349
Google Scholar
[15] Hirsch P B, 1952 Acta Crystallography 5 176
Google Scholar
[16] 麦振洪 2020 X射线衍射动力学: 理论与应用(北京: 科学出版社) 第10−49页
Mai Z H 2020 X-ray Diffraction Dynamics: Theory and Applications (Beijing: Science Press) pp10−49 (in Chinese)
[17] Zhao Z T, Xu H J 2004 Proceedings of European Particle Accelerator Conference Lucerne, Switzerland, June 5–9, 2004 p2368
[18] 杨俊亮, 李中亮, 李瑭, 朱晔, 宋丽, 薛莲, 张小威 2020 69 104101
Google Scholar
Yang J L, Li Z L, Li T, Zhu Y, Song L, Xue L, Zhang X W 2020 Acta Phys. Sin. 69 104101
Google Scholar
[19] Río M, Dejus R J 2011 Proc. Spie. 8141 259
[20] Zachariasen, W. H 1967 Phys. Rev. Lett. 18 195
Google Scholar
[21] del Rio M S, Perez-Bocanegra N, Shi X B, Honkimaki V, Zhang L 2015 J. Appl. Crystallogr. 48 477
Google Scholar
[22] Li Z L, Fan Y C, Xue L, Zhang Z Y, Wang J 2019 2019 AIP Conference Proceedings 2054 Taiwan, China, June 10−15, 2019 p060040
[23] Penning P, Polder D 1961 Philips Res. Rep. 16 419
DownLoad:
Catalog
Metrics
- Abstract views: 5273
- PDF Downloads: 185
- Cited By: 0
