-
A two-dimensional self-similarity transformation theory is established, and the focusing (parabolic) (2 + 1)-dimensional NLS equation is taken as the model. The two-dimensional self-similarity transformation is proposed for converting the focusing (2 + 1)-dimensional NLS equation into the focusing (1 + 1) dimensional NLS equations, and the excitation of its novel line-rogue waves is further investigated. It is found that the spatial coherent structures induced by the Akhmediev breathers (AB) and Kuznetsov-Ma solitons (KMS) also have the short-lived characteristics which are possessed by the line-rogue waves induced by the Peregrine solitons, and the other higher-order rogue waves and the multi-rogue waves of the (1 + 1) dimensional NLS equations. This is completely different from the evolution characteristics of spatially coherent structures induced by bright solitons (including multi-solitons and lump solutions), with their shapes and amplitudes kept unchanged. The diagram shows the evolution characteristics of all kinds of resulting line rogue waves. The new excitation mechanism of line rogue waves revealed contributes to the new understanding of the coherent structure of high-dimensional nonlinear wave models.
-
Keywords:
- rogue wave /
- line rogue wave /
- two-dimensional self-similar transformation /
- nonlinear Schrödinger equation
[1] Onorato M, Osborne A R, Serio M, Bertone S 2001 Phys. Rev. Lett. 86 5831
Google Scholar
[2] Kharif C, Pelinovsky E, Slunyaev A 2009 Rogue Waves in the Ocean. In: Advances in Geophysical and Environmental Mechanics and Mathematics (Berlin: Springer-Verlag)
[3] Adcock T A A, Taylor P H 2014 Rep. Prog. Phys. 77 105901
Google Scholar
[4] Dudley J M, Genty G, Eggleton B J 2008 Opt. Express 16 3644
Google Scholar
[5] Kasparian J, Bejot P, Wolf J P, Dudley J M 2009 Opt. Express 17 12070
Google Scholar
[6] Shukla P K, Moslem W M 2012 Phys. Lett. A 376 1125
Google Scholar
[7] Tsai Y Y, Tsai Y, Lin I 2016 Nature Phys. 12 573
Google Scholar
[8] Bludov Y V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610
Google Scholar
[9] Vinayagam P S, Radha R, Porsezian K 2013 Phys. Rev. E 88 042906
Google Scholar
[10] Ginzburg N S, Rozental R M, Sergeev A S, Fedotov A E, Zotova I V, Tarakanov V P 2017 Phys. Rev. Lett. 119 034801
Google Scholar
[11] Hohmann R, Kuhl U, Stockmann H J, Kaplan L, Heller E J 2010 Phys. Rev. Lett. 104 093901
Google Scholar
[12] Ganshin A N, Efimov V B, Kolmakov G V, Mezhov-Deglin L P, McClintock P V E 2008 Phys. Rev. Lett. 101 065303
Google Scholar
[13] Stenflo L, Marklund M 2010 J. Plasma Phys. 76 293
Google Scholar
[14] Hammani K, Kibler B, Finot C, Morin P, Millot G P 2011 Opt. Lett. 36 112
Google Scholar
[15] Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503
Google Scholar
[16] Yan Z Y 2011 Phys. Lett. A 375 4274
[17] Han J F, Liang T, Duan W S 2019 Euro. Phys. J. E 42 5
Google Scholar
[18] Copus M G, Camley R E 2020 Phys. Rev. B 102 220410
Google Scholar
[19] Dysthe K, Krogstad H, Muller P 2008 Ann. Rev. Flu. Mech. 40 287
Google Scholar
[20] Benetazzo A, Ardhuin F, Bergamasco F, Cavaleri L, Guimarães P V, Schwendeman M, Sclavo M, Thomson J, Torsello A 2017 Sci. Rep. 7 8276
[21] Peregrine D H 1983 J. Aust. Math. Soc. B 25 16
Google Scholar
[22] Akhmediev N, Korneev V I 1986 Theor. Math. Phys. 69 1089
Google Scholar
[23] Kuznetsov E 1977 Sov. Phys. Dokl. 22 507
Google Scholar
[24] Ma Y C 1979 Stud. Appl. Math. 60 43
[25] Akhmediev N, Ankiewicz A, Soto-Crespo J M 2009 Phys. Rev. E 80 026601
Google Scholar
[26] He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914
Google Scholar
[27] Dubard P, Matveev V B 2011 Nat. Hazards Earth Syst. Sci. 11 667
Google Scholar
[28] Ankiewicz A, Clarkson P A, Akhmediev N 2010 J. Phys. A 43 122002
Google Scholar
[29] Kedziora D J, Ankiewicz A, Akhmediev N 2011 Phys. Rev. E 84 056611
Google Scholar
[30] Zhao L C, Guo B, Ling L 2016 J. Math. Phys. 57 043508
Google Scholar
[31] Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F 2013 Phys. Rep. 528 47
Google Scholar
[32] Soto-Crespo J M, Devine N, Akhmediev N 2016 Phys. Rev. Lett. 116 103901
Google Scholar
[33] Akhmediev N, Dudley J M, Solli D R, Turitsyn S K 2013 J. Opt. 15 060201
Google Scholar
[34] Ohta Y, Yang J K 2012 Proc. R. Soc. Lond. Ser. A 468 1716
Google Scholar
[35] Christian K, Efim P 2003 Euro. J. Mech. B Fluids 22 603
[36] Wang L H, He J S, Xu H, Wang J, Porsezian K 2017 Phys. Rev. E 95 042217
Google Scholar
[37] Dudley J M, Dias F, Erkintalo M, Genty G 2014 Nature Photo. 8 755
Google Scholar
[38] Zhang X E, Chen Y, Tang X Y 2018 Comput. Math. Appl. 76 1938
Google Scholar
[39] Chen J C, Chen Y, Feng B F, Maruno K, Ohta Y 2018 J. Phys. Soc. Jpn. 87 094007
Google Scholar
[40] Wang M M, Chen Y 2021 Nonlinear Dyn. 104 2621
Google Scholar
[41] Wang M M, Chen Y 2021 Nonlinear Dyn. 98 1781
Google Scholar
[42] Birkholz S, Nibbering E T J 2013 Phys. Rev. Lett. 111 243903
Google Scholar
[43] Solli D R Ropers C, Koonath P, Jalali B 2007 Nature 450 1054
Google Scholar
[44] Solli D R, Ropers C, Jalali B 2008 Phys. Rev. Lett. 101 233902
Google Scholar
[45] Kibler B, Fatome J, Finot C, Millot G, Genty G, Wetzel B, Akhmediev N, Dias F, Dudley J M 2012 Sci. Rep. 2 463
Google Scholar
[46] Chabchoub A, Hoffmannn N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502
Google Scholar
[47] Bailung H, Sharma S K, Nakamura Y 2011 Phys. Rev. Lett. 107 255005
Google Scholar
[48] Xiong H, Gan J H, Wu Y 2017 Phys. Rev. Lett. 119 153901
Google Scholar
[49] 张解放, 金美贞, 胡文成 2020 69 244205
Google Scholar
Zhang J F, Jin M Z, Hu W C 2020 Acta Phys. Sin. 69 244205
Google Scholar
[50] 张解放, 金美贞 2020 69 214203
Google Scholar
Zhang J F, Jin M Z 2020 Acta Phys. Sin. 69 214203
Google Scholar
[51] Martin D U, Yuen H C 1980 Wave Motion 2 215
Google Scholar
[52] Carter J D, Segur H 2003 Phys. Rev. E 68 045601
Google Scholar
[53] Manakov S V 1974 Sov. Phys. JETP 38 248
[54] Pecseli H L 1985 IEEE Trans. Plasma Sci. 13 53
Google Scholar
[55] Gross E P 1963 J. Math Phys. 4 195
Google Scholar
[56] Pitaevskii L P 1961 Sov. Phys. JETP 13 451
Google Scholar
[57] Benney D J, Roskes G J 1969 Stud. Appl. Math. 48 377
Google Scholar
[58] Myra J R and Liu C S 1980 Phys. Fluids 23 2258
Google Scholar
[59] Gorza S P, Roig N 2004 Phys. Rev. Lett. 92 084101
Google Scholar
[60] Gorza S P, Kockaert P, Emplit P, Haelterman M 2009 Phys. Rev. Lett. 102 13410
Google Scholar
[61] Fermann M E 2000 Phys. Rev. Lett. 84 6010
Google Scholar
[62] Ankiewicz A, Kedziora D J, Akhmediev N 2011 Phys. Lett. A 375 2782
Google Scholar
[63] Kedziora D J, Ankiewicz A, Akhmediev N 2012 Phys. Rev. E 86 056602
Google Scholar
[64] Ohta Y, Yang J K 2012 Proc. R. Soc. A 468 1716
Google Scholar
[65] Kimmoun O, Hsu H C, Branger H, Li M S, Chen Y Y, Kharif C, Onorato M, Kelleher E J R, Kibler B, Akhmediev N, Chabchoub A 2016 Sci. Rep. 6 8516
Google Scholar
-
图 1 一阶单线怪波(28)在
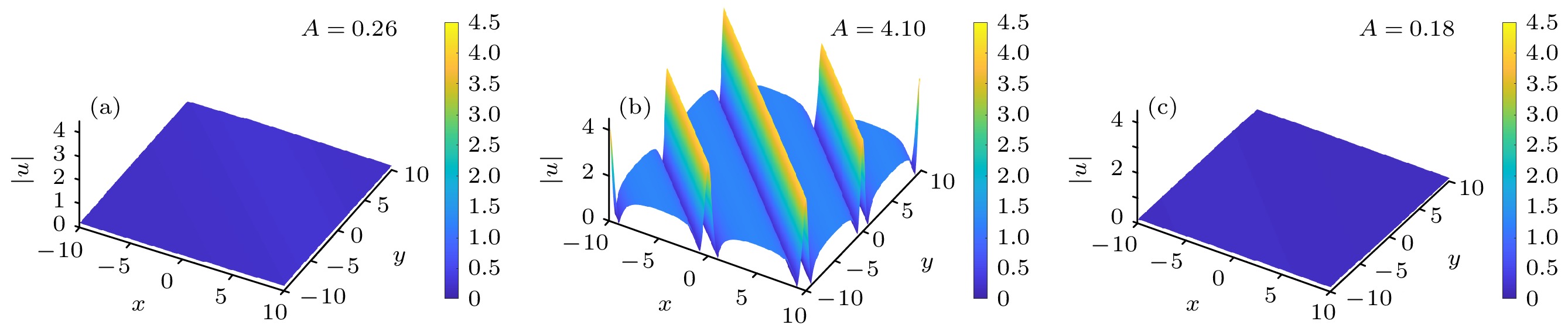
$ (x, y) $ -平面上随$ t $ 的演化图: (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ , 自由参数选取为$\alpha = \beta = \lambda = 1,$ $\gamma = 2, {\kappa _0} = {\iota _0} = - {a_0} = {{ {b}}_0} = 1$ Figure 1. Evolution plots of the first-order single line-rogue wave (28) with the
$ t $ on the$ (x, y) $ -plane. (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ . The free parameters are chosen as$ \alpha = \beta = 1, $ $\gamma = 2, {\kappa _0} = {\iota _0} = -{a_0} = {{ {b}}_0} = 1$ 
图 2 二阶单线怪波(29)在
$ (x, y) $ -平面上随$ t $ 的演化图: (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ , 自由参数选取为$ \alpha = \beta = \lambda = 1, $ $\gamma = 2, {\kappa _0} = {\iota _0} = -{a_0} = {{{b}}_0} = 1$ ,$ {\xi _d} = {\tau _d} = 0 $ Figure 2. Evolution plots of the second-order single line-rogue wave (29) with the
$ t $ on the$ (x, y) $ -plane. (a)$ t = - 3 $ ; (b)$ t = $ $ 0 $ ; (c)$ t = 5 $ . The free parameters are chosen as$ \alpha = \beta = 1, $ $\gamma = 2, {\kappa _0} = {\iota _0} = -{a_0} = {{{b}}_0} = 1, {\xi _d} = {\tau _d} = 0$ 
图 3 双线怪波(37)在
$ (x, y) $ -平面上随$ t $ 的演化图: (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ , 自由参数选取为$\alpha = $ $ \beta = \lambda = 1,$ $\gamma = 2, {\kappa _0} = {\iota _0} = -{a_0} = {{ {b}}_0} = 1$ ,$\delta = 25, \mu = 100$ Figure 3. Evolution plots of the double line-rogue wave (37) with
$ t $ on the$ (x, y) $ -plane. (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ .The free parameters are chosen as$ \alpha = \beta = 1, $ $\gamma = 2,~ {\kappa _0} = {\iota _0} = -{a_0} = {{ {b}}_0} = 1, ~\delta = 25, \mu = 100$ 
图 4 多线怪波(38)在
$ (x, y) $ -平面上随$ t $ 的演化图: (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ , 自由参数选取为$ \alpha = \beta = \lambda = 1, $ $\gamma = 2, {\kappa _0} = {\iota _0} = -{a_0} = {{ {b}}_0} = 1$ ,$a = 0.45$ Figure 4. Evolution plots of the multi-line rogue wave (38) with
$ t $ on the$ (x, y) $ -plane. (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ . The free parameters are chosen as$ \alpha = \beta = 1, $ $\gamma = 2, {\kappa _0} = {\iota _0} = -{a_0} = {{ {b}}_0} = 1, a = 0.45$ 
图 5 线怪波(39)在
$ (x, y) $ -平面上随$ t $ 的演化图 (a)$ t = - 3 $ , (b)$ t = 0 $ , (c)$ t = 5 $ , 自由参数选取为$ \alpha = \beta = \lambda = 1, $ $\gamma = 2, $ $ {\kappa _0} = {\iota _0} = -{a_0} = {{ {b}}_0} = 1$ ,$a = 0.45$ Figure 5. Evolution plots of the line rogue waves (39) with
$ t $ on the$ (x, y) $ -plane. (a)$ t = - 3 $ ; (b)$ t = 0 $ ; (c)$ t = 5 $ . The free parameters are chosen as$ \alpha = \beta = 1, $ $\gamma = 2, {\kappa _0} = {\iota _0} = -{a_0} = {{ {b}}_0} = 1, a = 0.45$ -
[1] Onorato M, Osborne A R, Serio M, Bertone S 2001 Phys. Rev. Lett. 86 5831
Google Scholar
[2] Kharif C, Pelinovsky E, Slunyaev A 2009 Rogue Waves in the Ocean. In: Advances in Geophysical and Environmental Mechanics and Mathematics (Berlin: Springer-Verlag)
[3] Adcock T A A, Taylor P H 2014 Rep. Prog. Phys. 77 105901
Google Scholar
[4] Dudley J M, Genty G, Eggleton B J 2008 Opt. Express 16 3644
Google Scholar
[5] Kasparian J, Bejot P, Wolf J P, Dudley J M 2009 Opt. Express 17 12070
Google Scholar
[6] Shukla P K, Moslem W M 2012 Phys. Lett. A 376 1125
Google Scholar
[7] Tsai Y Y, Tsai Y, Lin I 2016 Nature Phys. 12 573
Google Scholar
[8] Bludov Y V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610
Google Scholar
[9] Vinayagam P S, Radha R, Porsezian K 2013 Phys. Rev. E 88 042906
Google Scholar
[10] Ginzburg N S, Rozental R M, Sergeev A S, Fedotov A E, Zotova I V, Tarakanov V P 2017 Phys. Rev. Lett. 119 034801
Google Scholar
[11] Hohmann R, Kuhl U, Stockmann H J, Kaplan L, Heller E J 2010 Phys. Rev. Lett. 104 093901
Google Scholar
[12] Ganshin A N, Efimov V B, Kolmakov G V, Mezhov-Deglin L P, McClintock P V E 2008 Phys. Rev. Lett. 101 065303
Google Scholar
[13] Stenflo L, Marklund M 2010 J. Plasma Phys. 76 293
Google Scholar
[14] Hammani K, Kibler B, Finot C, Morin P, Millot G P 2011 Opt. Lett. 36 112
Google Scholar
[15] Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503
Google Scholar
[16] Yan Z Y 2011 Phys. Lett. A 375 4274
[17] Han J F, Liang T, Duan W S 2019 Euro. Phys. J. E 42 5
Google Scholar
[18] Copus M G, Camley R E 2020 Phys. Rev. B 102 220410
Google Scholar
[19] Dysthe K, Krogstad H, Muller P 2008 Ann. Rev. Flu. Mech. 40 287
Google Scholar
[20] Benetazzo A, Ardhuin F, Bergamasco F, Cavaleri L, Guimarães P V, Schwendeman M, Sclavo M, Thomson J, Torsello A 2017 Sci. Rep. 7 8276
[21] Peregrine D H 1983 J. Aust. Math. Soc. B 25 16
Google Scholar
[22] Akhmediev N, Korneev V I 1986 Theor. Math. Phys. 69 1089
Google Scholar
[23] Kuznetsov E 1977 Sov. Phys. Dokl. 22 507
Google Scholar
[24] Ma Y C 1979 Stud. Appl. Math. 60 43
[25] Akhmediev N, Ankiewicz A, Soto-Crespo J M 2009 Phys. Rev. E 80 026601
Google Scholar
[26] He J S, Zhang H R, Wang L H, Porsezian K, Fokas A S 2013 Phys. Rev. E 87 052914
Google Scholar
[27] Dubard P, Matveev V B 2011 Nat. Hazards Earth Syst. Sci. 11 667
Google Scholar
[28] Ankiewicz A, Clarkson P A, Akhmediev N 2010 J. Phys. A 43 122002
Google Scholar
[29] Kedziora D J, Ankiewicz A, Akhmediev N 2011 Phys. Rev. E 84 056611
Google Scholar
[30] Zhao L C, Guo B, Ling L 2016 J. Math. Phys. 57 043508
Google Scholar
[31] Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F 2013 Phys. Rep. 528 47
Google Scholar
[32] Soto-Crespo J M, Devine N, Akhmediev N 2016 Phys. Rev. Lett. 116 103901
Google Scholar
[33] Akhmediev N, Dudley J M, Solli D R, Turitsyn S K 2013 J. Opt. 15 060201
Google Scholar
[34] Ohta Y, Yang J K 2012 Proc. R. Soc. Lond. Ser. A 468 1716
Google Scholar
[35] Christian K, Efim P 2003 Euro. J. Mech. B Fluids 22 603
[36] Wang L H, He J S, Xu H, Wang J, Porsezian K 2017 Phys. Rev. E 95 042217
Google Scholar
[37] Dudley J M, Dias F, Erkintalo M, Genty G 2014 Nature Photo. 8 755
Google Scholar
[38] Zhang X E, Chen Y, Tang X Y 2018 Comput. Math. Appl. 76 1938
Google Scholar
[39] Chen J C, Chen Y, Feng B F, Maruno K, Ohta Y 2018 J. Phys. Soc. Jpn. 87 094007
Google Scholar
[40] Wang M M, Chen Y 2021 Nonlinear Dyn. 104 2621
Google Scholar
[41] Wang M M, Chen Y 2021 Nonlinear Dyn. 98 1781
Google Scholar
[42] Birkholz S, Nibbering E T J 2013 Phys. Rev. Lett. 111 243903
Google Scholar
[43] Solli D R Ropers C, Koonath P, Jalali B 2007 Nature 450 1054
Google Scholar
[44] Solli D R, Ropers C, Jalali B 2008 Phys. Rev. Lett. 101 233902
Google Scholar
[45] Kibler B, Fatome J, Finot C, Millot G, Genty G, Wetzel B, Akhmediev N, Dias F, Dudley J M 2012 Sci. Rep. 2 463
Google Scholar
[46] Chabchoub A, Hoffmannn N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502
Google Scholar
[47] Bailung H, Sharma S K, Nakamura Y 2011 Phys. Rev. Lett. 107 255005
Google Scholar
[48] Xiong H, Gan J H, Wu Y 2017 Phys. Rev. Lett. 119 153901
Google Scholar
[49] 张解放, 金美贞, 胡文成 2020 69 244205
Google Scholar
Zhang J F, Jin M Z, Hu W C 2020 Acta Phys. Sin. 69 244205
Google Scholar
[50] 张解放, 金美贞 2020 69 214203
Google Scholar
Zhang J F, Jin M Z 2020 Acta Phys. Sin. 69 214203
Google Scholar
[51] Martin D U, Yuen H C 1980 Wave Motion 2 215
Google Scholar
[52] Carter J D, Segur H 2003 Phys. Rev. E 68 045601
Google Scholar
[53] Manakov S V 1974 Sov. Phys. JETP 38 248
[54] Pecseli H L 1985 IEEE Trans. Plasma Sci. 13 53
Google Scholar
[55] Gross E P 1963 J. Math Phys. 4 195
Google Scholar
[56] Pitaevskii L P 1961 Sov. Phys. JETP 13 451
Google Scholar
[57] Benney D J, Roskes G J 1969 Stud. Appl. Math. 48 377
Google Scholar
[58] Myra J R and Liu C S 1980 Phys. Fluids 23 2258
Google Scholar
[59] Gorza S P, Roig N 2004 Phys. Rev. Lett. 92 084101
Google Scholar
[60] Gorza S P, Kockaert P, Emplit P, Haelterman M 2009 Phys. Rev. Lett. 102 13410
Google Scholar
[61] Fermann M E 2000 Phys. Rev. Lett. 84 6010
Google Scholar
[62] Ankiewicz A, Kedziora D J, Akhmediev N 2011 Phys. Lett. A 375 2782
Google Scholar
[63] Kedziora D J, Ankiewicz A, Akhmediev N 2012 Phys. Rev. E 86 056602
Google Scholar
[64] Ohta Y, Yang J K 2012 Proc. R. Soc. A 468 1716
Google Scholar
[65] Kimmoun O, Hsu H C, Branger H, Li M S, Chen Y Y, Kharif C, Onorato M, Kelleher E J R, Kibler B, Akhmediev N, Chabchoub A 2016 Sci. Rep. 6 8516
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4762
- PDF Downloads: 75
- Cited By: 0
