-
The decoherence of entanglement states stored in quantum memory is a major obstacle when implementing a quantum repeater. So far, the electron spins in quantum dots are usually utilized to construct entangled states in quantum repeater. In the quantum repeater process, the distance between quantum dots is large, so the interaction between them can be neglected. Thus the hyperfine interaction between the electron spin and its neighbor nuclear spins in the quantum dot is considered to be the main reason for the decoherence of the system. In early researches, the hyperfine interaction between the electron spin and its neighbor nuclear spins was considered as an effective magnetic field whose magnitude and direction are random and the magnitude follows the Gaussian distribution. In this paper, we simultaneously consider an applied magnetic field and the interaction between the electron spin and its neighbor nuclear spins, and investigate the decoherence of the quantum repeater of two quantum dots. We first solve the time evolution of the system by the numerical method, and the result shows that when the applied magnetic field is increased to a certain value, the four Bell states can be divided into two kinds, each with two Bell states. The system cannot transit from the Bell state in one kind to that in the other kind, but can transit between two Bell states with in the same kind. This effectively improves the fidelity of the initial state and suppresses the decoherence of the system. For a given applied magnetic field with large magnitude, we theoretically study the effect of the fluctuation of nuclear spin on the entangled state, and give an analytical expression for each of the fidelity and the decoherence time of the initial state. We show that the decoherence times of the four Bell states are the same, but the time evolutions of the Bell states belonging to different kinds are different obviously. The fidelity of two Bell states not only decays exponentially but also oscillates rapidly, so such two Bell states are difficult to be manipulated and not suggested in quantum repeater process. The results in this paper are expected to provide theoretical suggestions for selecting the entangled states in quantum repeater.
-
Keywords:
- quantum teleportation /
- quantum repeater /
- decoherence of entanglement state /
- quantum fidelity
[1] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wotter W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[2] Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575
Google Scholar
[3] Ma X S, Herbst T, Scheidl, Wang D, Kropatschek S, Naylor W, Wittmann A, Mech J, Korfler E, Anisimova, Makarov V, Jennewein T, Ursin R, Zeilinger A 2012 Nature 489 269
Google Scholar
[4] Vallone G, Bacco D, Dequal D, Gaiarin S, Luceri V, Bianco G, Villoresi P 2015 Phys. Rev. Lett. 115 040502
Google Scholar
[5] Yin J, Cao Y, Li Y H, Ren J G, Liao S K, Zhang L, Cai W Q, Liu W Y, Li B, Dai H, Li M, Huang Y M, Deng L, Li L, Zhang Q, Liu L N, Chen Y A, Lu C Y, Shu R, Peng C Z, Wang J Y, Pan J W 2017 Phys. Rev. Lett. 119 200501
Google Scholar
[6] Yin J, Cao Y, Li Y H, Liao S K, Zhang L, Ren J G, Cai W Q, Liu W Y, Li B, Dai H, Li G B, Lu Q M, Gong Y H, Xu Y, Li S L, Li F Z, Yin Y Y, Jiang Z Q, Li M, Jia J J, Ren G, He D, Zhou Y L, Zhang X X, Wang N, Chang X, Zhu Z C, Liu N L, Chen Y A, Lu C Y, Shu R, Peng C Z, Wang J Y, Pan J W 2017 Science 356 1140
Google Scholar
[7] Dür W, Briegel H J, Cirac J I, Zoller P 1999 Phys. Rev. A 59 169
Google Scholar
[8] Pfister A D, Salz M, Hettrich M, Poschinger U G, Schmidt-Kaler F 2016 Appl. Phys. B 122 1
Google Scholar
[9] Greve K D 2013 Towards Solid-State Quantum Repeaters: Ultrafast, Coherent Optical Control and Spin-photon Entanglement in Charged InAs Quantum Dots (Heidelberg: Springer) pp21–39
[10] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
[11] Freer S, Simmons S, Laucht A, Muhonen J T, Dehollain J P, Kalra R, Mohiyaddin F A, Hudson F E, Itoh K M, McCallum J C, Jamieson D N, Dzurak A S, Morello A 2017 Quantum Sci. Technol. 2 015009
Google Scholar
[12] Kawakami E, Scarlino P, Ward D R, Braakman F R, Savage D E, Lagally M G, Friesen M, Coppersmith S N, Eriksson M A, Vandersypen L M K 2014 Nat. Nanotechnol. 9 666
Google Scholar
[13] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature. 473 190
[14] Loock van P, Ladd T D, Sanaka K, Yamaguchi F, Nemoto K, Munro W J, Yamamoto Y 2006 Phys. Rev. Lett. 96 240501
Google Scholar
[15] Duan L M, Lukin M, Cirac J I 2001 Nature 414 413
Google Scholar
[16] Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891
Google Scholar
[17] Lloyd S, Shahriar M S, Shapiro J H, Hemmer P R 2001 Phys. Rev. Lett. 87 167903
Google Scholar
[18] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[19] Malinowski F K, Martins F, Cywiński L, Rudner M S, Nissen P D, Fallahi S, Gardner G C, Manfra M J, Marcus C M, Kuemmeth F 2017 Phys. Rev. Lett. 118 177702
Google Scholar
[20] Liu R B, Yao W, Sham L 2007 New J. Phys. 9 226
Google Scholar
[21] Saito S, Zhu X B, Amsüss R, Matsuzaki Y, Kakuyanagi K, Shimo-Oka T, Mizuochi N, Nemoto K, Munro W J, Semba K 2013 Phys. Rev. Lett. 111 107008
Google Scholar
[22] Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623
Google Scholar
[23] Maune B M, Borselli M G, Huang B, Ladd T D, Deelman P W, Holabird K S, Kiselev A A, Alvarado-Rodriguez I, Ross R S, Schmitz A E 2012 Nature 481 344
Google Scholar
[24] Yao W, Liu R B, Sham L J 2007 Phys. Rev. Lett. 98 077602
Google Scholar
[25] Merkulov I A 2002 Phys. Rev. B 65 205309
Google Scholar
[26] Assali L V C, Petrilli H M, Capaz R B, Koiller B, Hu X D, Sarma S D 2011 Phys. Rev. B 83 165301
Google Scholar
[27] Eisenberg B, Sullivan R 2008 Math. Mag. 81 362
Google Scholar
[28] Reilly D J, Taylor J M, Laird E A, Petta J R, Marcus C M, Hanson M P, Gossard A C 2007 Phys. Rev. Lett. 101 236803
-
图 1 量子中继步骤 (a)在每一段量子传输线路上分发纠缠态; (b)在量子中继器中进行纠缠态的转移操作; (c) Alice做Bell基测量, 量子比特1的信息通过量子比特2和3组成的纠缠态量子信息传输通道远程传到Bob处
Figure 1. The process of quantum repeater: (a) Distributing entanglement states in every segment of quantum channel; (b) quantum swapping in quantum repeaters; (c) quantum teleportation. After Alice taking Bell state measurement, the information of qubit 1 is transferred to Bob via entanglement state of qubit 2 and 3.
图 2 两个相互纠缠的量子中继器, 纠缠态为两个电子自旋组成的4个Bell基.
Figure 2. Entanglement of the two separated quantum repeaters. Entangled states are the four Bell states constructed by two electron spins.
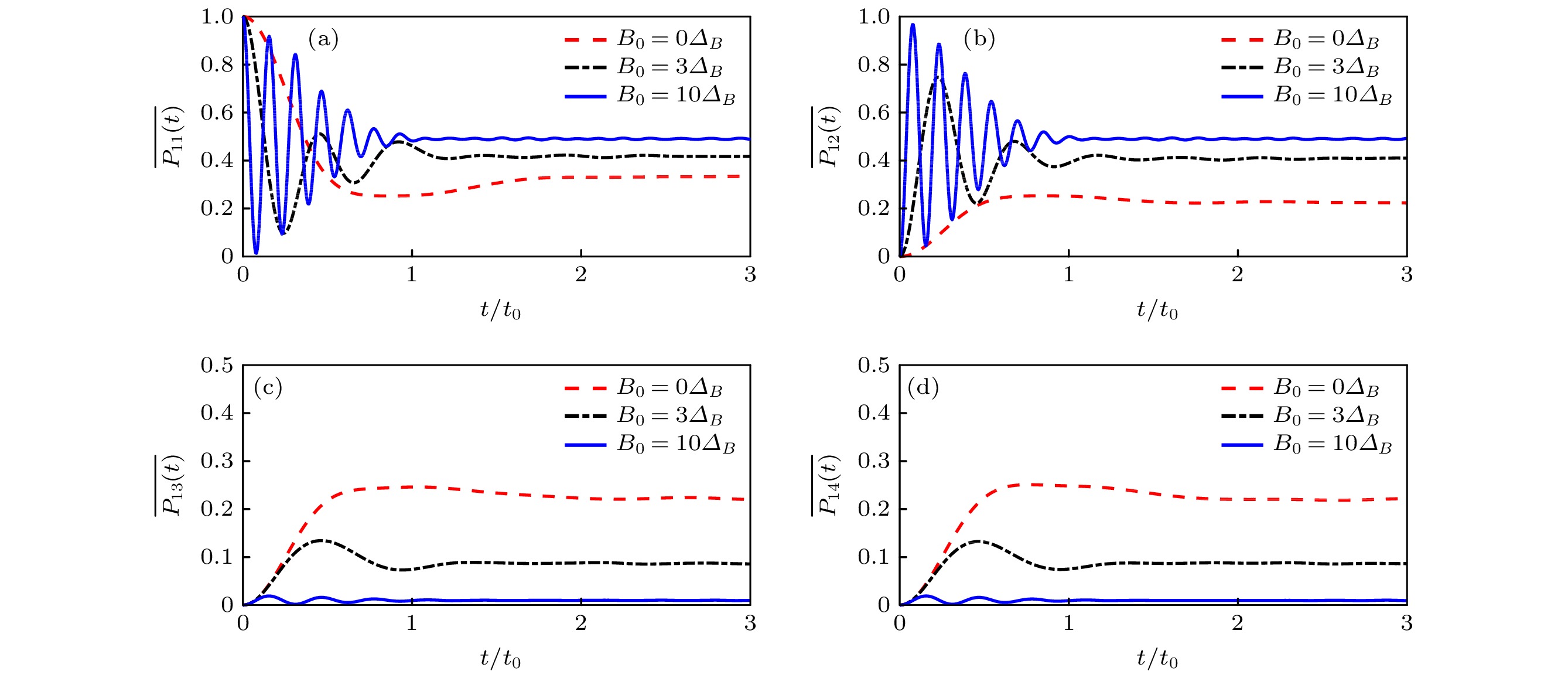
图 3 3种不同大小的外加磁场下, 体系处于4个不同Bell基上的几率随时间的演化规律 (a), (b), (c), (d)分别对应系统处于
$ |\phi_{12}^+\rangle $ ,$ |\phi_{12}^-\rangle $ ,$ |\psi_{12}^+\rangle $ ,$ |\psi_{12}^-\rangle $ 的平均几率. 体系初态为$ |\phi_{12}^+\rangle $ , 外加磁场参数为$ B_0 = 0 $ (红色虚线),$ B_0 = 3\varDelta_B $ (黑色点划线),$ B_0 = 10\varDelta_B $ (蓝色实线). 时间以$ t_0 = 1/(\mu_0\varDelta_B) $ 为单位Figure 3. Time evolution of mean probability in four Bell states: (a)
$ |\phi_{12}^+\rangle $ , (b)$ |\phi_{12}^-\rangle $ , (c)$ |\psi_{12}^+\rangle $ , (d)$ |\psi_{12}^-\rangle $ for different applied magnetic fields. The initial state is$ |\phi_{12}^+\rangle $ , and the parameters are$ B_0 = 0 $ (red dash line),$ B_0 = 3\varDelta_B $ (black dash dot line),$ B_0 = 10\varDelta_B $ (blue solid line). Time is in the unit of$ t_0 = 1/(\mu_0\varDelta_B) $ .
图 4 3种不同大小的外加磁场下, 体系处于4个不同Bell基上的几率随时间的演化规律 (a), (b), (c), (d)分别对应系统处于
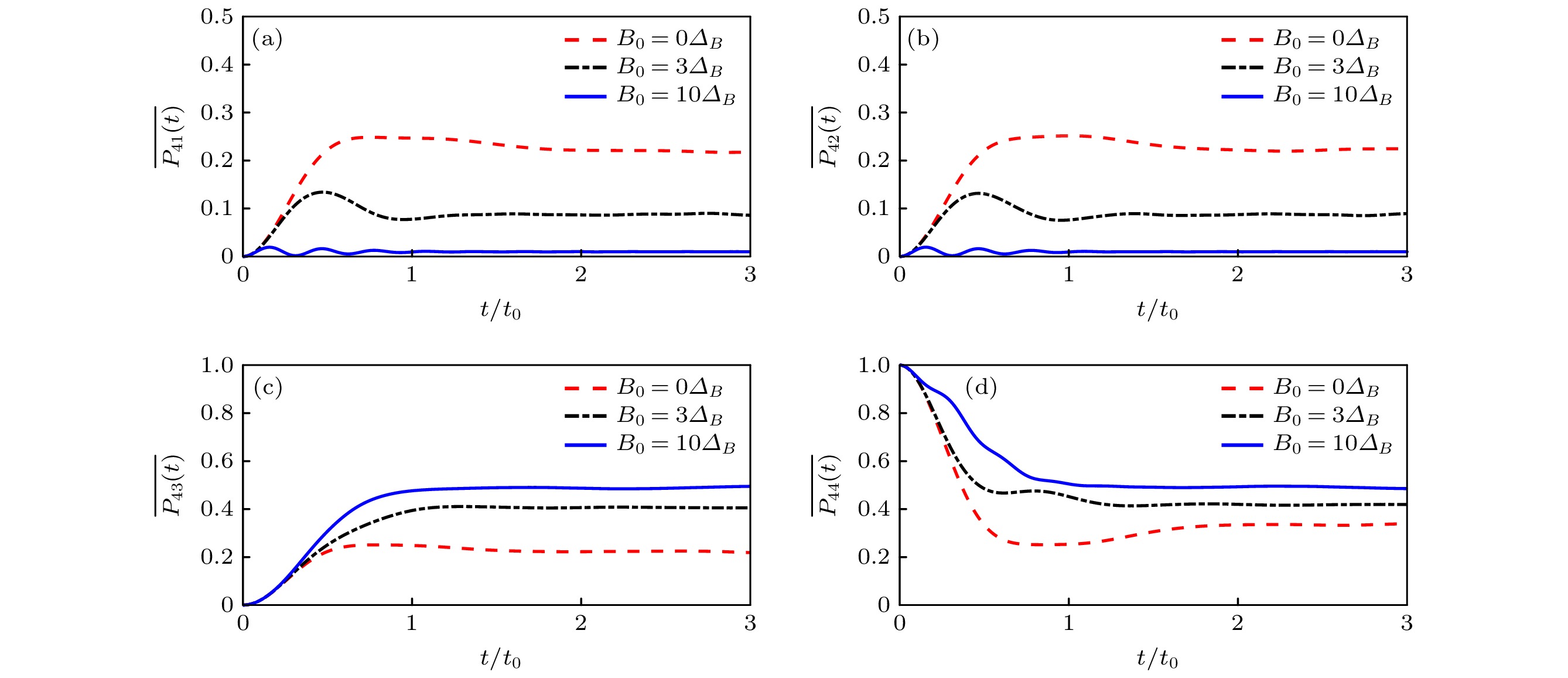
$ |\phi_{12}^+\rangle $ ,$ |\phi_{12}^-\rangle $ ,$ |\psi_{12}^+\rangle $ ,$ |\psi_{12}^-\rangle $ 的平均几率. 体系的初态为$ |\psi_{12}^+\rangle $ , 外加磁场参数为$ B_0 = 0 $ (红色虚线),$ B_0 = 3\varDelta_B $ (黑色点划线)、$ B_0 = 10\varDelta_B $ (蓝色实线). 时间以$ t_0 = 1/(\mu_0\varDelta_B) $ 为单位Figure 4. Time evolution of mean probability in four Bell states: (a)
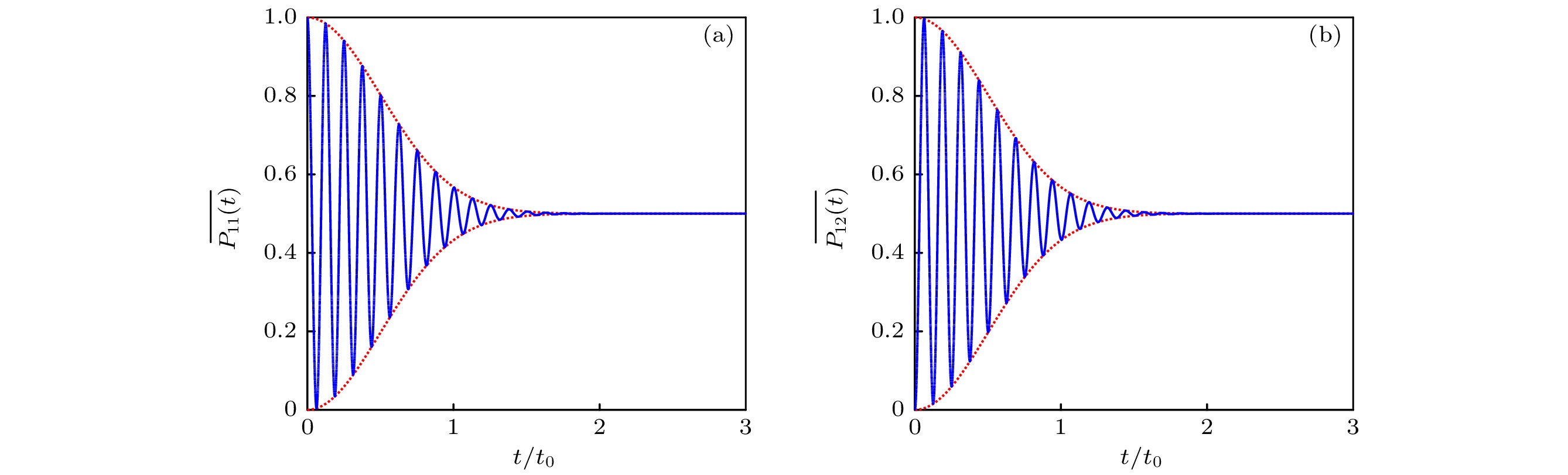
$ |\phi_{12}^+\rangle $ , (b)$ |\phi_{12}^-\rangle $ , (c)$ |\psi_{12}^+\rangle $ , (d)$ |\psi_{12}^-\rangle $ for different applied magnetic fields. The initial state is$ |\psi_{12}^+\rangle $ , and the parameters are$ B_0 = 0 $ (red dash line),$ B_0 = 3\varDelta_B $ (black dash dot line),$ B_0 = 10\varDelta_B $ (blue solid line). Time is in the unit of$ t_0 = 1/(\mu_0\varDelta_B) $ .
图 5 (a)系统仍然处在
$ |\phi_{12}^+\rangle $ 上的平均几率随时间的演化; (b)系统跃迁到$ |\phi_{12}^-\rangle $ 的平均几率随时间的演化. 系统初态为$ |\phi_{12}^+\rangle $ , 时间以$t_0 = 1/(\mu_0\varDelta_B)$ 为单位Figure 5. (a) Time evolution of the mean probability in
$ |\phi_{12}^+\rangle $ , (b) that in$ |\phi_{12}^{-}\rangle $ . The initial state is$ |\phi_{12}^+\rangle $ , and the time is in the unit of$t_0 = 1/(\mu_0\varDelta_B)$ .
图 6 (a)系统仍然处在
$ |\psi_{12}^+\rangle $ 上的平均几率随时间的演化; (b)系统跃迁到$ |\psi_{12}^-\rangle $ 的平均几率随时间的演化. 系统初态为$ |\psi_{12}^+\rangle $ , 时间以$t_0 = 1/(\mu_0\varDelta_B)$ 为单位Figure 6. (a) Time evolution of the mean probability in
$ |\psi_{12}^+\rangle $ , (b) that in$ |\psi_{12}^-\rangle $ . The initial state is$ |\psi_{12}^+\rangle $ , and the time is in the unit of$t_0 = 1/(\mu_0\varDelta_B)$ . -
[1] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wotter W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[2] Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575
Google Scholar
[3] Ma X S, Herbst T, Scheidl, Wang D, Kropatschek S, Naylor W, Wittmann A, Mech J, Korfler E, Anisimova, Makarov V, Jennewein T, Ursin R, Zeilinger A 2012 Nature 489 269
Google Scholar
[4] Vallone G, Bacco D, Dequal D, Gaiarin S, Luceri V, Bianco G, Villoresi P 2015 Phys. Rev. Lett. 115 040502
Google Scholar
[5] Yin J, Cao Y, Li Y H, Ren J G, Liao S K, Zhang L, Cai W Q, Liu W Y, Li B, Dai H, Li M, Huang Y M, Deng L, Li L, Zhang Q, Liu L N, Chen Y A, Lu C Y, Shu R, Peng C Z, Wang J Y, Pan J W 2017 Phys. Rev. Lett. 119 200501
Google Scholar
[6] Yin J, Cao Y, Li Y H, Liao S K, Zhang L, Ren J G, Cai W Q, Liu W Y, Li B, Dai H, Li G B, Lu Q M, Gong Y H, Xu Y, Li S L, Li F Z, Yin Y Y, Jiang Z Q, Li M, Jia J J, Ren G, He D, Zhou Y L, Zhang X X, Wang N, Chang X, Zhu Z C, Liu N L, Chen Y A, Lu C Y, Shu R, Peng C Z, Wang J Y, Pan J W 2017 Science 356 1140
Google Scholar
[7] Dür W, Briegel H J, Cirac J I, Zoller P 1999 Phys. Rev. A 59 169
Google Scholar
[8] Pfister A D, Salz M, Hettrich M, Poschinger U G, Schmidt-Kaler F 2016 Appl. Phys. B 122 1
Google Scholar
[9] Greve K D 2013 Towards Solid-State Quantum Repeaters: Ultrafast, Coherent Optical Control and Spin-photon Entanglement in Charged InAs Quantum Dots (Heidelberg: Springer) pp21–39
[10] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
[11] Freer S, Simmons S, Laucht A, Muhonen J T, Dehollain J P, Kalra R, Mohiyaddin F A, Hudson F E, Itoh K M, McCallum J C, Jamieson D N, Dzurak A S, Morello A 2017 Quantum Sci. Technol. 2 015009
Google Scholar
[12] Kawakami E, Scarlino P, Ward D R, Braakman F R, Savage D E, Lagally M G, Friesen M, Coppersmith S N, Eriksson M A, Vandersypen L M K 2014 Nat. Nanotechnol. 9 666
Google Scholar
[13] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature. 473 190
[14] Loock van P, Ladd T D, Sanaka K, Yamaguchi F, Nemoto K, Munro W J, Yamamoto Y 2006 Phys. Rev. Lett. 96 240501
Google Scholar
[15] Duan L M, Lukin M, Cirac J I 2001 Nature 414 413
Google Scholar
[16] Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891
Google Scholar
[17] Lloyd S, Shahriar M S, Shapiro J H, Hemmer P R 2001 Phys. Rev. Lett. 87 167903
Google Scholar
[18] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[19] Malinowski F K, Martins F, Cywiński L, Rudner M S, Nissen P D, Fallahi S, Gardner G C, Manfra M J, Marcus C M, Kuemmeth F 2017 Phys. Rev. Lett. 118 177702
Google Scholar
[20] Liu R B, Yao W, Sham L 2007 New J. Phys. 9 226
Google Scholar
[21] Saito S, Zhu X B, Amsüss R, Matsuzaki Y, Kakuyanagi K, Shimo-Oka T, Mizuochi N, Nemoto K, Munro W J, Semba K 2013 Phys. Rev. Lett. 111 107008
Google Scholar
[22] Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623
Google Scholar
[23] Maune B M, Borselli M G, Huang B, Ladd T D, Deelman P W, Holabird K S, Kiselev A A, Alvarado-Rodriguez I, Ross R S, Schmitz A E 2012 Nature 481 344
Google Scholar
[24] Yao W, Liu R B, Sham L J 2007 Phys. Rev. Lett. 98 077602
Google Scholar
[25] Merkulov I A 2002 Phys. Rev. B 65 205309
Google Scholar
[26] Assali L V C, Petrilli H M, Capaz R B, Koiller B, Hu X D, Sarma S D 2011 Phys. Rev. B 83 165301
Google Scholar
[27] Eisenberg B, Sullivan R 2008 Math. Mag. 81 362
Google Scholar
[28] Reilly D J, Taylor J M, Laird E A, Petta J R, Marcus C M, Hanson M P, Gossard A C 2007 Phys. Rev. Lett. 101 236803
DownLoad:
Catalog
Metrics
- Abstract views: 4920
- PDF Downloads: 87
- Cited By: 0
