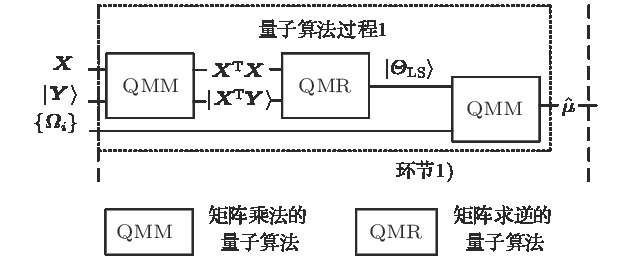
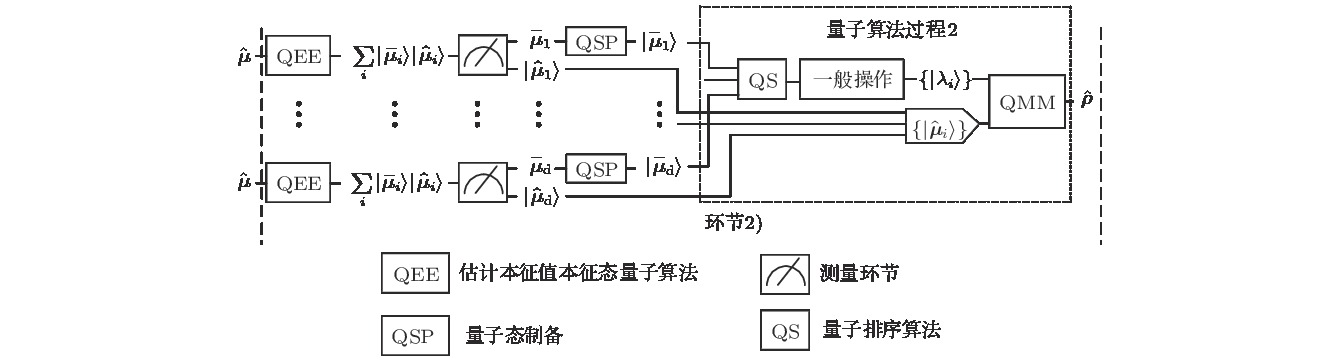
-
Recently, we try to answer the following question: what will happen to our life if quantum computers can be physically realized. In this research, we explore the impact of quantum algorithms on the time complexity of quantum state tomography based on the linear regression algorithm if quantum states can be efficiently prepared by classical information and quantum algorithms can be implemented on quantum computers. By studying current quantum algorithms based on quantum singular value decomposition (SVE) of calculating matrix multiplication, solving linear equations and eigenvalue and eigenstate estimation and so on, we propose a novel scheme to complete the mission of quantum state tomography. We show the calculation based on our algorithm as an example at last. Although quantum state preparations and extra measurements are indispensable in our quantum algorithm scheme compared with the existing classical algorithm, the time complexity of quantum state tomography can be remarkably declined. For a quantum system with dimension d, the entire quantum scheme can reduce the time complexity of quantum state tomography from
$ O(d^{4}) $ to$ O(d\mathrm{poly}\log d) $ when both the condition number$ \kappa $ of related matrices and the reciprocal of precision$ \varepsilon $ are$ O(\mathrm{poly}\log d) $ , and quantum states of the same order$ O(d) $ can be simultaneously prepared. This is in contrast to the observation that quantum algorithms can reduce the time complexity of quantum state tomography to$O(d^3) $ when quantum states can not be efficiently prepared. In other words, the preparing of quantum states efficiently has become a bottleneck constraining the quantum acceleration.-
Keywords:
- quantum algorithm /
- quantum state tomography /
- time complexity
[1] Teo Y S 2016 Introduction to quantum-state estimation (Singapore: World Scientific Press) pp1−5, 23−31
[2] Häffner H, Hänsel W, Roos C, et al 2005 Nature 438 643
Google Scholar
[3] James D F V, Kwiat P G, Munro W J, et al. 2001 Phys. Rev. A 64 052312
Google Scholar
[4] Qi B, Hou Z, Li L, et al. 2013 Sci. Rep. 3 3496
Google Scholar
[5] Hou Z, Zhong H-S, Tian Y, et al. 2016 New J. Phys. 18 083036
Google Scholar
[6] Blume-Kohout R 2010 Phys. Rev. Lett. 105 200504
Google Scholar
[7] Teo Y S, Zhu H, Englert B G, et al. 2011 Phys. Rev. Lett. 107 020404
Google Scholar
[8] Blume-Kohout R 2010 New J. Phys. 12 043034
Google Scholar
[9] Huszár F, Houlsby N M T 2012 Phys. Rev. A 85 052120
Google Scholar
[10] Shor P W 1999 SIREV 41 303
Google Scholar
[11] Abrams D S, Lloyd S 1999 Phys. Rev. Lett. 83 5162
Google Scholar
[12] Harrow A W, Hassidim A, Lloyd S 2009 Phys. Rev. Lett. 103 150502
Google Scholar
[13] Wiebe N, Braun D, Lloyd S 2012 Phys. Rev. Lett. 109 050505
Google Scholar
[14] 陆思聪, 郑昱, 王晓霆, 吴热冰 2017 控制理论与应用 34 1429
Lu S C, Zheng Y, Wang X T, Wu R B 2017 Contl. Theor. Appl. 34 1429
[15] Smolin J A, Gambetta J M, Smith G 2012 Phys. Rev. Lett. 108 070502
Google Scholar
[16] [17] Wossnig L, Zhao Z K, Prakash A 2018 Phys. Rev. Lett. 120 050502
Google Scholar
[18] Høyer P, Neerbek J, Shi Y 2002 Algorithmica 34 429
Google Scholar
[19] Cheng S T, Wang C Y 2006 IEEE Trans. Circuits Syst. I: Reg. Papers 53 316
Google Scholar
[20] Kerenidis I, Prakash A 2017 Proceedings of 8th Innovations in Theoretical Computer Science Conference Berkeley, CA, USA, January 9−11, 2017 p1
[21] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (10th Anniversary Edition) (Cambridge: Cambridge University Press) pp185−188
-
图 1 基于线性回归估计的经典重构算法
Figure 1. Classical algorithm of quantum state tomography via linear regression
图 2 整体量子算法简明过程
Figure 2. Concise process of the whole quantum algorithm
图 3 量子算法过程1: 基于线性回归模型重构算法的量子算法
Figure 3. Quantum algorithm process 1: quantum algorithm based on quantum state tomography via linear regression
图 4 量子算法过程2
Figure 4. Quantum algorithm process 2
表 1 量子态重构过程不同环节的量子算法与经典算法时间复杂度的对比
Table 1. Time complexity comparison of each step between quantum algorithm and classical algorithm for reconstructing quantum state
算法过程 时间复杂度 量子态制备过程: 经典 量子 1) ${ X}\rightarrow|{ X}\rangle$ — $O(d\log (d)/\varepsilon ^2)$ 2) ${ Y}\rightarrow|{ Y}\rangle$ — $O(d\log (d)/\varepsilon ^2)$ 3) $\{\varOmega_i\}\rightarrow\{|\varOmega_i\rangle\}$ — $O(d\log (d)/\varepsilon ^2)$ 最小二乘求解过程: 经典 量子 1) ${ X}^{\rm T}{ X}$ $O(d^4)$ $O(\kappa^3 d/\varepsilon )$ 2) $({ X}^{\rm T}{ X})^{-1}$ $O(d^4)$ $O(\kappa^2\sqrt{d}\mathrm{poly}\log(d)/\varepsilon )$ 3) ${ X}^{\rm T}{ Y}$ $O(d^4)$ $O(\kappa^3 d/\varepsilon )$ 使用估计出的参数重构密度矩阵$\hat{\mu}$: 经典 量子 1) ${ I}/d+\sum_{i=1}^{d}\hat{\varTheta}_i\varOmega_i$ $O(d^4)$ $O(\kappa^3 d/\varepsilon )$ 寻找与矩阵$\hat{\mu}$最接近的目标密度矩阵$\hat{\rho}$: 经典 量子 1) 求解矩阵$\hat{\mu}$的本征值和本征态$\{|\bar{\mu}_i\rangle|\hat{\mu}_i\rangle\}$ $O(d^3)$ $O(\kappa\sqrt{r}\mathrm{poly}\log d/\varepsilon )$ 2) 测量得到$\hat{\mu}$本征值数值$\{\bar{\mu} _i\}$ — $O(d)$ 3) 将$\hat{\mu}$的本征值数据制备成量子态 $\{\bar{\mu} _i\}\rightarrow\{|\bar{\mu} _i\rangle\}$ — $O(d\log(d)/\varepsilon ^2)$ 4) 对矩阵$\hat{\mu}$的本征值进行排序 $O(d)$ $O((\log d)^2)$ 5) 一般运算得到矩阵$\hat{\rho}$的本征值$\{\lambda_i\}$或$\{|\lambda_i\rangle\}$ $O(d)$ $O(d)$ 6) 由$\hat{\rho}$的本征值及$\{|\hat{\mu}_i\rangle\}$得到$\hat{\rho}=\sum_i\lambda_i|\hat{\mu}_i\rangle\langle\hat{\mu}_i|$ $O(d^3)$ $O(\kappa^3 \sqrt{d}/\varepsilon )$ 
DownLoad: CSV
表 A1 求解厄米矩阵本征值和本征态的量子算法[17]
Table A1. Quantum algorithm for calculating the eigenvalues and eigenstates of Hermite matrix[17]
1) 制备输入态$|{{b}}\rangle=\sum_i\beta_i|{{v}}_i\rangle$, 其中${{v}}_i$是矩阵A的奇异向量 2) 分别对矩阵A及${ A}+\eta { I}$使用奇异值估计算法, 精度$\delta<1/2\kappa$并且$\eta=1/\kappa$, 得到$\sum_i\beta_i|{{v}}_i\rangle_{ A}||\bar{\lambda}_i|\rangle_B||\bar{\lambda}_i+\eta|\rangle_C\rangle$ 3) 增加一辅助寄存器D, 当寄存器B的值大于C 时, 将D置为1, 然后应用一受控于此辅助位的条件相位门: $\qquad\sum_i(-1)^{f_i}\beta_i|{{v}}_i\rangle_{ A}||\bar{\lambda}_i|\rangle_B||\bar{\lambda}_i+\eta|\rangle_C\rangle|f_i\rangle_D$ 4) 对寄存器C进行量子算法的逆运算, 得到态 $\qquad\sum_i(-1)^{f_i}\beta_i|{{v}}_i\rangle_{ A}||\bar{\lambda}_i|\rangle_B|f_i\rangle_D$ 5) 将奇异向量$|{{v}}_i\rangle_{ A}$转化到矩阵的本征态$|{{\mu}}_i\rangle_{ A}$上: 相应于正本征值的奇异向量不变, 相应于负本征值的奇异向量乘以–1 , 得到 $\qquad\sum_i(-1)^{f_i}\beta_i|{{\mu}}_i\rangle_{ A}||\bar{\lambda}_i|\rangle_B$
DownLoad: CSV
-
[1] Teo Y S 2016 Introduction to quantum-state estimation (Singapore: World Scientific Press) pp1−5, 23−31
[2] Häffner H, Hänsel W, Roos C, et al 2005 Nature 438 643
Google Scholar
[3] James D F V, Kwiat P G, Munro W J, et al. 2001 Phys. Rev. A 64 052312
Google Scholar
[4] Qi B, Hou Z, Li L, et al. 2013 Sci. Rep. 3 3496
Google Scholar
[5] Hou Z, Zhong H-S, Tian Y, et al. 2016 New J. Phys. 18 083036
Google Scholar
[6] Blume-Kohout R 2010 Phys. Rev. Lett. 105 200504
Google Scholar
[7] Teo Y S, Zhu H, Englert B G, et al. 2011 Phys. Rev. Lett. 107 020404
Google Scholar
[8] Blume-Kohout R 2010 New J. Phys. 12 043034
Google Scholar
[9] Huszár F, Houlsby N M T 2012 Phys. Rev. A 85 052120
Google Scholar
[10] Shor P W 1999 SIREV 41 303
Google Scholar
[11] Abrams D S, Lloyd S 1999 Phys. Rev. Lett. 83 5162
Google Scholar
[12] Harrow A W, Hassidim A, Lloyd S 2009 Phys. Rev. Lett. 103 150502
Google Scholar
[13] Wiebe N, Braun D, Lloyd S 2012 Phys. Rev. Lett. 109 050505
Google Scholar
[14] 陆思聪, 郑昱, 王晓霆, 吴热冰 2017 控制理论与应用 34 1429
Lu S C, Zheng Y, Wang X T, Wu R B 2017 Contl. Theor. Appl. 34 1429
[15] Smolin J A, Gambetta J M, Smith G 2012 Phys. Rev. Lett. 108 070502
Google Scholar
[16] [17] Wossnig L, Zhao Z K, Prakash A 2018 Phys. Rev. Lett. 120 050502
Google Scholar
[18] Høyer P, Neerbek J, Shi Y 2002 Algorithmica 34 429
Google Scholar
[19] Cheng S T, Wang C Y 2006 IEEE Trans. Circuits Syst. I: Reg. Papers 53 316
Google Scholar
[20] Kerenidis I, Prakash A 2017 Proceedings of 8th Innovations in Theoretical Computer Science Conference Berkeley, CA, USA, January 9−11, 2017 p1
[21] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (10th Anniversary Edition) (Cambridge: Cambridge University Press) pp185−188
DownLoad:
Catalog
Metrics
- Abstract views: 11697
- PDF Downloads: 254
- Cited By: 0
