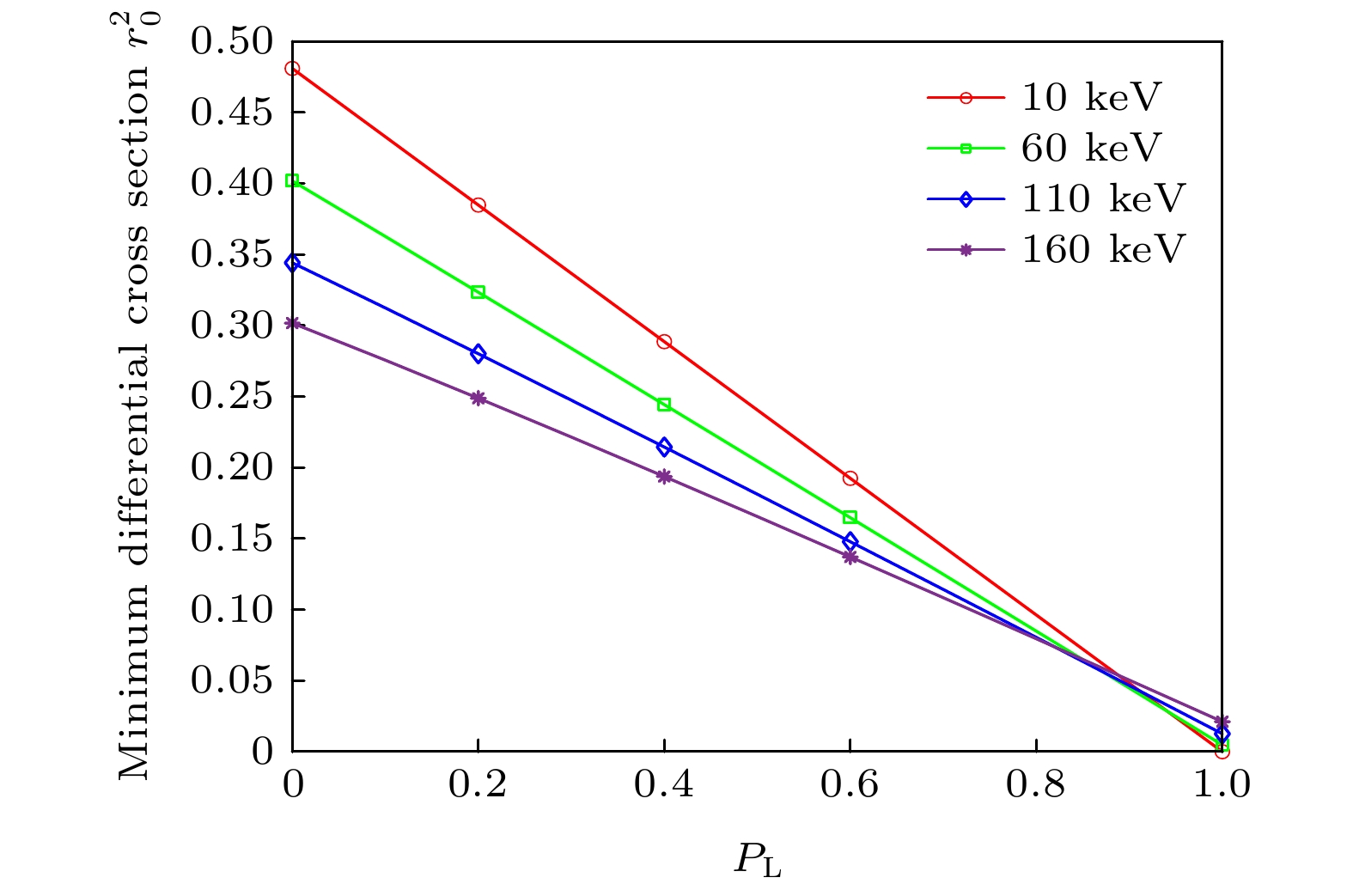
-
X-ray fluorescence computed tomography (XFCT) is a molecular imaging technique with great potential applications in biomedical imaging, in which used is the primary X-ray to excite element probes with high atomic number inside samples or tissues for functional imaging. However, owing to the limitation of molecular sensitivity and spatial resolution, the XFCT has not been widely used in the molecular imaging. A large number of Compton scattering photons are produced as the broadband primary X-ray passes through the samples or tissues, forming a strong noise background in the collected XRF signal, which is a major cause of limited molecular sensitivity. Therefore, eliminating the Compton scattering noise is very important for improving molecular sensitivity. In this paper, we summarize the main physical processes involved in the imaging process of XFCT, including the angle distribution and polarization state of the fluorescence and Compton scattering photons, fluorescence yield and deexcitation time of K-shell vacancy. The above physical processes are the main limitations of the imaging quality of XFCT. Through the derivation and analysis of physical processes, we explore the possibility of using these physical effects to reduce the Compton scattering noise and draw some conclusions below. 1) The deexcitation time of K-shell vacancy of the element with high atomic number is very short, consequently the scattered light and fluorescence cannot be distinguished between each other under the time resolution condition of the existing detector. 2) The angular distribution of the K-shell fluorescence emission is isotropic, and the differential cross section of Compton scattering reaches a minimum value near the polarization direction of the incident light of which the minimum decreases as the linear polarization degree of the incident light increases. Therefore, the polarized light source is beneficial to reducing the Compton scattering noise. 3) The linear degree of polarization of K-shell fluorescence is zero, while the Compton scattering photons possess a certain linear degree of polarization in some scattering directions, so the difference between polarization states may be helpful in reducing the Compton scattering noise.
-
Keywords:
- X-ray fluorescence /
- computed tomography /
- polarized X-rays /
- Compton scattering /
- functional imaging
[1] Boisseau P, Grodzins L 1987 Hyperfine Interact. 33 283
Google Scholar
[2] Cheong S K, Jones B L, Siddiqi A K, Liu F, Manohar N, Cho S H 2010 Phys. Med. Biol. 55 647
Google Scholar
[3] Bazalova M, Kuang Y, Pratx G, Xing L 2012 IEEE Trans. Med. Imaging 31 1620
Google Scholar
[4] Sjölin M, Danielsson M 2014 Phys. Med. Biol. 59 6507
Google Scholar
[5] Li L, Zhang S Y, Li R Z, Chen Z Q 2017 Opt. Eng. 56 043106
Google Scholar
[6] Zhang S Y, Li L, Chen Z Q 2019 IEEE Access 7 113589
Google Scholar
[7] Li L, Li R Z, Zhang S Y, Chen Z Q 2016 Proc. of SPIE 9967 99670F
Google Scholar
[8] Zhang S Y, Li L, Chen J Y, Chen Z Q, Zhang W L, Lu H B 2019 Int. J. Mol. Sci. 20 2315
Google Scholar
[9] Ahmad M, Bazalova M, Xiang L, Xing L 2014 IEEE Trans. Med. Imaging 33 1119
Google Scholar
[10] Sasaya T, Sunaguchi N, Hyodo K, Zeniya T, Takeda T, Yuasa T 2017 Sci. c Rep. 7 44143
Google Scholar
[11] Chi Z, Du Y, Huang W, Tang C 2020 J. Synchrotron Radiat. 27 737
Google Scholar
[12] Vernekohl D, Tzoumas S, Zhao W, Xing L 2018 Med. Phys. 45 3741
Google Scholar
[13] Mcmaster W H 1961 Rev. Mod. Phys. 33 8
Google Scholar
[14] Jones J A, D’Addario A J, Rojec B L, Milione G, Galvez E J 2016 Am. J. Phys. 84 822
Google Scholar
[15] Bambynek W, Crasemann B, Fink R W, Freund H U, Mark H, Swift C D, Price R E, Rao P V 1972 Rev. Mod. Phys. 44 716
Google Scholar
[16] Hubbell JH, Trehan PN, Singh N, Chand B, Mehta D, Garg ML, Garg RR, Singh S, Puri S 1994 J. Phys. Chem. Ref. Data 23 339
Google Scholar
[17] Ertuğral B, Apaydın G, Çevik U, Ertuğrul M, Kobya A İ 2007 Radiat. Phys. Chem. 76 15
Google Scholar
[18] Scofield J H 1974 Phys. Rev. A 9 1041
Google Scholar
[19] Schaart D R 2021 Phys. Med. Biol. 66 09TR01
Google Scholar
[20] Han I, Şahin M, Demir L 2008 Can. J. Phys 86 361
Google Scholar
[21] E G Berezhko, N M Kabachnik 1977 J. Phys. B:At. Mol. Phys. 10 2467
Google Scholar
[22] Kämpfer T, Uschmann I, Wu Z W, Surzhykov A, Fritzsche S, Förster E, Paulus G G 2016 Phys. Rev. A 93 033409
Google Scholar
[23] 柳钰, 徐忠锋, 王兴, 曾利霞, 刘婷 2020 69 043201
Google Scholar
Liu Y, Xu Z F, Wang X, Zeng L X, Liu T 2020 Acta Phys. Sin. 69 043201
Google Scholar
[24] Kahlon K S, Aulakh H S, Singh N, Mittal R, Allawadhi K L, Sood B S 1991 Phy. Rev. A 43 1455
Google Scholar
[25] Depaola G O 2003 Nucl. Instrum. Methods Phys. Res., Sect. A 512 619
Google Scholar
[26] Matt G, Feroci M, Rapisarda M, Costa E 1996 Radiat. Phys. Chem. 48 403
Google Scholar
[27] Fano U 1949 JOSA 39 859
Google Scholar
[28] Hamzawy A 2016 Radiat. Phys. Chem. 119 103
Google Scholar
[29] Hubbell J H 1997 Radiat. Phys. Chem. 50 113
Google Scholar
[30] Hubbell J H, Veigele W J, Briggs E A, Brown R T, Cromer D T, Howerton D R 1975 J. Phys. Chem. Ref. Data 4 471
Google Scholar
[31] Hubbell J H, O/verbo/ I 1979 J. Phys. Chem. Ref. Data 8 69
Google Scholar
[32] Chantler C T 1995 J. Phys. Chem. Ref. Data 24 71
Google Scholar
[33] Tartari A, Taibi A, Bonifazzi C, Baraldi C 2002 Phys. Med. Biol. 47 163
Google Scholar
[34] Zhang L, YangDai T Y 2016 Appl. Radiat. Isot. 114 179
Google Scholar
-
图 1 基于小孔成像方式的XFCT实验设置
Figure 1. Experimental setup based on pinhole imaging.
图 2 偏振康普顿散射示意图
Figure 2. Schematic diagram of polarized Compton scattering.
图 3 不同入射能量时,
${\theta _{{\rm{min}}}}$ 随线偏振度变化Figure 3.
${\theta _{{\rm{min}}}}$ varying with polarization for different incident energy.
图 4 不同入射能量时最小微分截面随偏振度的变化
Figure 4. Minimum differential cross section varying with polarization for different incident energy.
图 5
$\varphi = 0{\rm{ , \pi }}$ 处微分截面随散射角变化 (a)${P_{\rm{L}}} = 1$ 时相干、非相干和总微分截面; (b) 不同线偏振度时的总微分截面; (c)${P_{\rm{L}}} = $ $ {\rm{0}}{\rm{.5}}$ 时不同入射能量下的总微分截面Figure 5. Differential cross section varying with
$\theta $ at$\varphi = 0{\rm{ , \pi }}$ : (a) Incoherent, coherent and total differential cross section at${P_{\rm{L}}} = 1$ ; (b) total differential cross section varying with$\theta $ for different${P_{\rm{L}}}$ ; (c) total differential cross section varying with$\theta $ for different incident energy at${P_{\rm{L}}} = {\rm{0}}{\rm{.5 }}$ 
图 6
$\varphi = 0\;{\rm{ or\; \pi }}$ 处$ \xi _2^{({\rm{f}})} $ 随散射角变化Figure 6.
$ \xi _2^{({\rm{f}})} $ varying with$ \theta $ at$\varphi = 0,\;{\rm{\pi }}$ .
图 7 不同能量下
$\theta = {\rm{π}}/2{\rm{ , }}\varphi = 0,\;{\rm{\;\pi }}$ 处散射光线偏振度随入射光线偏振度变化Figure 7. The linear polarization of scattering photons
$ P_{\rm{L}}^{({\rm{f}})} $ varying with$ P_{\rm{L}}^{({\rm{i}})} $ at$\theta = {\rm{π}}/2{\rm{ , }}~\varphi = 0,\;{\rm{ \pi }}$ for different incident energy. -
[1] Boisseau P, Grodzins L 1987 Hyperfine Interact. 33 283
Google Scholar
[2] Cheong S K, Jones B L, Siddiqi A K, Liu F, Manohar N, Cho S H 2010 Phys. Med. Biol. 55 647
Google Scholar
[3] Bazalova M, Kuang Y, Pratx G, Xing L 2012 IEEE Trans. Med. Imaging 31 1620
Google Scholar
[4] Sjölin M, Danielsson M 2014 Phys. Med. Biol. 59 6507
Google Scholar
[5] Li L, Zhang S Y, Li R Z, Chen Z Q 2017 Opt. Eng. 56 043106
Google Scholar
[6] Zhang S Y, Li L, Chen Z Q 2019 IEEE Access 7 113589
Google Scholar
[7] Li L, Li R Z, Zhang S Y, Chen Z Q 2016 Proc. of SPIE 9967 99670F
Google Scholar
[8] Zhang S Y, Li L, Chen J Y, Chen Z Q, Zhang W L, Lu H B 2019 Int. J. Mol. Sci. 20 2315
Google Scholar
[9] Ahmad M, Bazalova M, Xiang L, Xing L 2014 IEEE Trans. Med. Imaging 33 1119
Google Scholar
[10] Sasaya T, Sunaguchi N, Hyodo K, Zeniya T, Takeda T, Yuasa T 2017 Sci. c Rep. 7 44143
Google Scholar
[11] Chi Z, Du Y, Huang W, Tang C 2020 J. Synchrotron Radiat. 27 737
Google Scholar
[12] Vernekohl D, Tzoumas S, Zhao W, Xing L 2018 Med. Phys. 45 3741
Google Scholar
[13] Mcmaster W H 1961 Rev. Mod. Phys. 33 8
Google Scholar
[14] Jones J A, D’Addario A J, Rojec B L, Milione G, Galvez E J 2016 Am. J. Phys. 84 822
Google Scholar
[15] Bambynek W, Crasemann B, Fink R W, Freund H U, Mark H, Swift C D, Price R E, Rao P V 1972 Rev. Mod. Phys. 44 716
Google Scholar
[16] Hubbell JH, Trehan PN, Singh N, Chand B, Mehta D, Garg ML, Garg RR, Singh S, Puri S 1994 J. Phys. Chem. Ref. Data 23 339
Google Scholar
[17] Ertuğral B, Apaydın G, Çevik U, Ertuğrul M, Kobya A İ 2007 Radiat. Phys. Chem. 76 15
Google Scholar
[18] Scofield J H 1974 Phys. Rev. A 9 1041
Google Scholar
[19] Schaart D R 2021 Phys. Med. Biol. 66 09TR01
Google Scholar
[20] Han I, Şahin M, Demir L 2008 Can. J. Phys 86 361
Google Scholar
[21] E G Berezhko, N M Kabachnik 1977 J. Phys. B:At. Mol. Phys. 10 2467
Google Scholar
[22] Kämpfer T, Uschmann I, Wu Z W, Surzhykov A, Fritzsche S, Förster E, Paulus G G 2016 Phys. Rev. A 93 033409
Google Scholar
[23] 柳钰, 徐忠锋, 王兴, 曾利霞, 刘婷 2020 69 043201
Google Scholar
Liu Y, Xu Z F, Wang X, Zeng L X, Liu T 2020 Acta Phys. Sin. 69 043201
Google Scholar
[24] Kahlon K S, Aulakh H S, Singh N, Mittal R, Allawadhi K L, Sood B S 1991 Phy. Rev. A 43 1455
Google Scholar
[25] Depaola G O 2003 Nucl. Instrum. Methods Phys. Res., Sect. A 512 619
Google Scholar
[26] Matt G, Feroci M, Rapisarda M, Costa E 1996 Radiat. Phys. Chem. 48 403
Google Scholar
[27] Fano U 1949 JOSA 39 859
Google Scholar
[28] Hamzawy A 2016 Radiat. Phys. Chem. 119 103
Google Scholar
[29] Hubbell J H 1997 Radiat. Phys. Chem. 50 113
Google Scholar
[30] Hubbell J H, Veigele W J, Briggs E A, Brown R T, Cromer D T, Howerton D R 1975 J. Phys. Chem. Ref. Data 4 471
Google Scholar
[31] Hubbell J H, O/verbo/ I 1979 J. Phys. Chem. Ref. Data 8 69
Google Scholar
[32] Chantler C T 1995 J. Phys. Chem. Ref. Data 24 71
Google Scholar
[33] Tartari A, Taibi A, Bonifazzi C, Baraldi C 2002 Phys. Med. Biol. 47 163
Google Scholar
[34] Zhang L, YangDai T Y 2016 Appl. Radiat. Isot. 114 179
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6254
- PDF Downloads: 96
- Cited By: 0
