-
A free-space quantum key distribution (QKD) system based on mobile equipment can provide an effective method to construct a real-time full-coverage multi-node network. However, the existing free-space QKD systems based on mobile devices encounter the challenge regarding the lack of stability caused by equipment disturbance. The robustness of the QKD polarization encoder against mobile device disturbance will be significant. Owing to the inevitable disturbance in practical applications, even the polarization-maintaining fiber (PMF) cannot maintain its polarization-maintaining characteristics well, which in turn affects the stability of some systems based on PMF. Therefore, in order to ensure that stable coding can be achieved under disturbances, we propose a two-way differential modulation mode, in which stable coding can still be achieved even under disturbances. At the same time, in order to verify the actual anti-disturbance characteristics of the mode, the polarization-modulated unit (PMU) with a two-way differential modulation mode is used in this study to generate four long-term stable polarization states subjected to the disturbances with a frequency of 200 Hz. At the same time, the PMU has a higher insertion loss, which makes the influence of crosstalk on the system more obvious. We also discuss two ways i.e. the time domain and frequency domain, to reduce the crosstalk which is caused by the imperfection of the device. The experiment is performed at a repetition frequency of 250 MHz, and a commercial avalanche single-photon detector is used to detect the system’s quantum bit error rate (QBER). Under the condition of no disturbance, the average QBER is 0.39% in 2 h. Then a vibration of approximately 200 Hz is used to simulate the practical disturbances, the average QBER is 0.36% in 2 h, and the fluctuation range of the QBER is only within 0.2%. We propose the first feasible encoding scheme in disturbed environments to ensure the long-term stability of the encoded polarization states, which is expected to be used in the multi-node expansion of the quantum network.
[1] Gisin N, Ribordy G, Tittel W, Zbinden H 2001 Rev. Mod. Phys. 74 145
Google Scholar
[2] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[3] Scarani V, Bechmann P H, Cerf N J, Dušek M, Lütkenhaus N, Peev M 2009 Rev. Mod. Phys. 81 1301
Google Scholar
[4] Gobby C, Yuan Z L, Shields A J 2004 Appl. Phys. Lett. 84 37628
Google Scholar
[5] Yin H L, Chen T Y, Yu Z W, Liu H, You L X, Zhou Y H, Chen S J, Mao Y, Huang M Q, Zhang W J, Chen H, Li M J, Nolan D, Zhou F, Jiang X, Wang Z, Zhang Q, Wang X B, Pan J W 2016 Phys. Rev. Lett. 117 190501
Google Scholar
[6] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W, Hu X L, Guan J Y, Yu Z W, Xu H, Lin J 2020 Phys. Rev. Lett. 124 070501
Google Scholar
[7] Wang J Y, Yang B, Liao S K, Zhang L, Shen Q, Hu X F, Wu J C, Yang S J, Jiang H, Tang Y L 2013 Nat. Photonics 7 387
Google Scholar
[8] Nauerth S, Moll F, Rau M, Fuchs C, Horwath J, Frick S, Weinfurter H 2013 Nat. Photonics 7 382
Google Scholar
[9] Liao S K, Cai W Q, Liu W Y, Zhang L, Li Y, Ren J G, Yin J, Shen Q, Cao Y, Li Z P 2017 Nature 549 43
Google Scholar
[10] Hill A D, Chapman J, Herndon K, Chopp C, Gauthier D J, Kwiat P 2017 Urbana 51 61801
Google Scholar
[11] Liu H Y, Tian X H, Gu C, Fan P, Ni X, Yang R, Zhang J N, Hu M, Niu Y, Cao X 2020 Nat. Sci. Rev. 7 921
Google Scholar
[12] Liao S K, Yong H L, Liu C, Shentu G L, Li D D, Lin J, Dai H, Zhao S Q, Li B, Guan J Y 2017 Nat. Photonics 11 509
Google Scholar
[13] Chen H, Wang J, Tang B, Li Z, Sun S H 2020 Opt. Lett. 45 3022
Google Scholar
[14] Xue Y, Shi L, Wei J, Yu L, Yu H, Tang J, Zhang Z 2020 Int. J. Theor. Phys. 59 3299
Google Scholar
[15] Pugh C J, Kaiser S, Bourgoin J P, Jin J, Sultana N, Agne S, Anisimova E, Makarov V, Choi E, Higgins B L 2017 Quantum Sci. Technol. 2 024009
Google Scholar
[16] Bourgoin J P, Higgins B L, Gigov N, Holloway C, Pugh C J, Kaiser S, Cranmer M, Jennewein T 2015 Opt. Express 23 33437
Google Scholar
[17] DeCesare A, Snyder R, Carvalho D, Miller W A, Alsing P M, Ahn D 2020 Proc. SPIE 11391 1139105
Google Scholar
[18] Liu X, Liao C, Tang Z, Wang J, Liu S 2007 Proc. SPIE 6827 682701
Google Scholar
[19] Liu X, Liao C, Mi J, Wang J, Liu S 2008 Phys. Lett. A 373 54
Google Scholar
[20] Lucio-Martinez I, Chan P, Mo X, Hosier S, Tittel W 2009 New J. Phys. 11 095001
Google Scholar
[21] Grunenfelder F, Boaron A, Rusca D, Martin A, Zbinden H 2018 Appl. Phys. Lett. 112 051108
Google Scholar
[22] Li Y, Li Y H, Xie H B, Li Z P, Peng C Z 2019 Opt. Lett. 44 5262
Google Scholar
[23] Agnesi C, Avesani M, Stanco A, Villoresi P, Vallone G 2019 Opt. Lett. 44 2398
Google Scholar
[24] Avesani M, Agnesi C, Stanco A, Vallone G, Villoresi P 2020 Opt. Lett. 45 4706
Google Scholar
[25] Wang J, Qin X, Jiang Y, Wang X, Chen L, Zhao F, Wei Z, Zhang Z 2016 Opt. Express 24 8302
Google Scholar
[26] Yuan Y, Du C, Shen Q, Wang J, Yu Y, Wei Z, Chen Z, Zhang Z 2020 Opt. Express 28 10772
Google Scholar
-
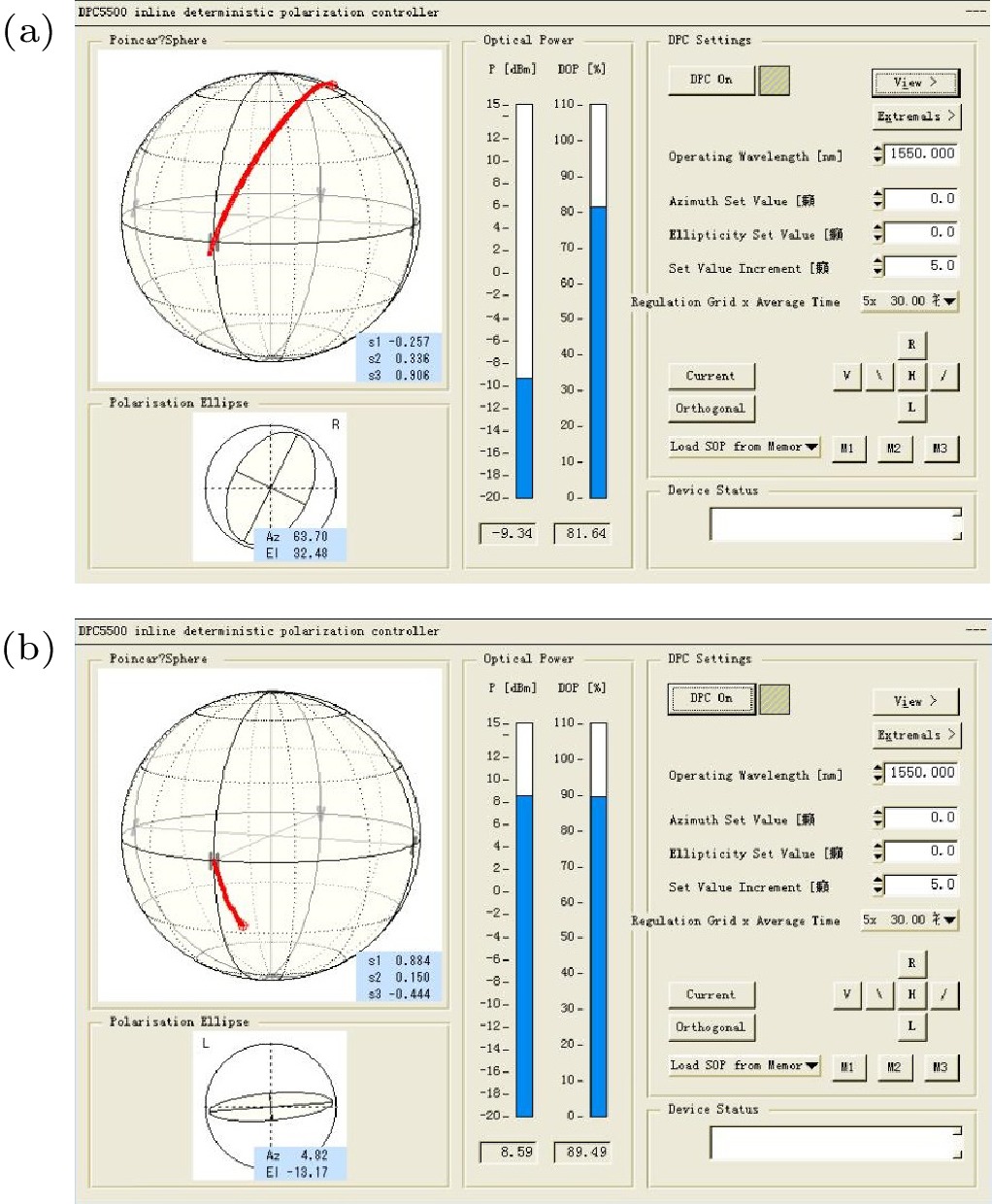
图 1 PMF在扰动环境下的测试, 图中红线表示偏振态在邦加球上的变化轨迹 (a) 在扰动情况下, 光在PMF快轴和慢轴上均有分量的偏振态变化; (b) 在扰动情况下, 光仅在PMF慢轴上传输时的偏振态变化
Figure 1. Testing of the PMF under a disturbance, the red line represents the change in the polarization state on the Poincare sphere: (a) Polarization state change with components on both the fast axis and the slow axis of the PMF under a disturbance; (b) polarization state change when light transmits only along the PMF slow axis under a disturbance.
图 2 相位调制偏振编码方案
Figure 2. Phase modulation polarization coding scheme.
图 3 PMU结构示意图
Figure 3. PMU structure diagram.
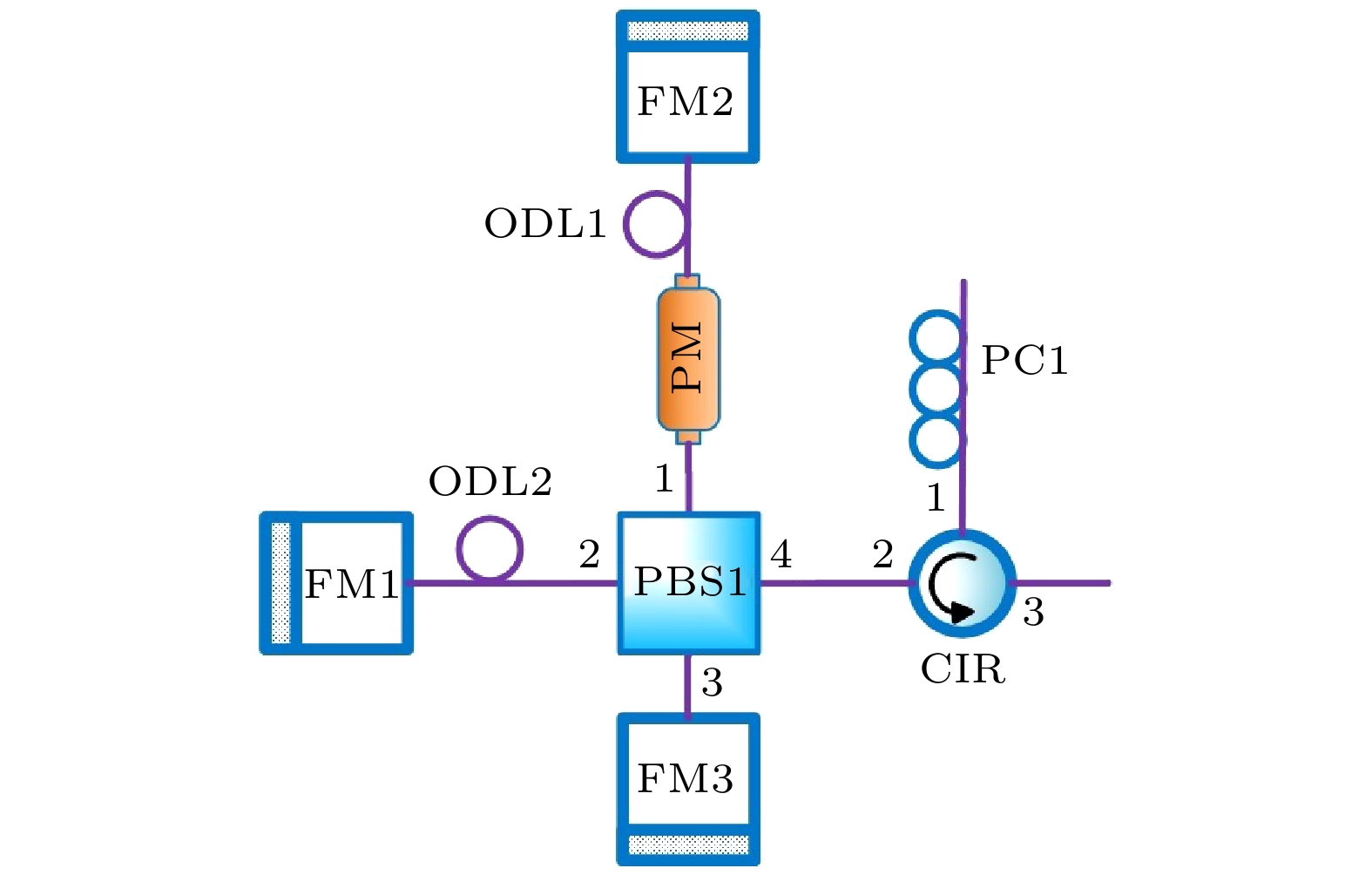
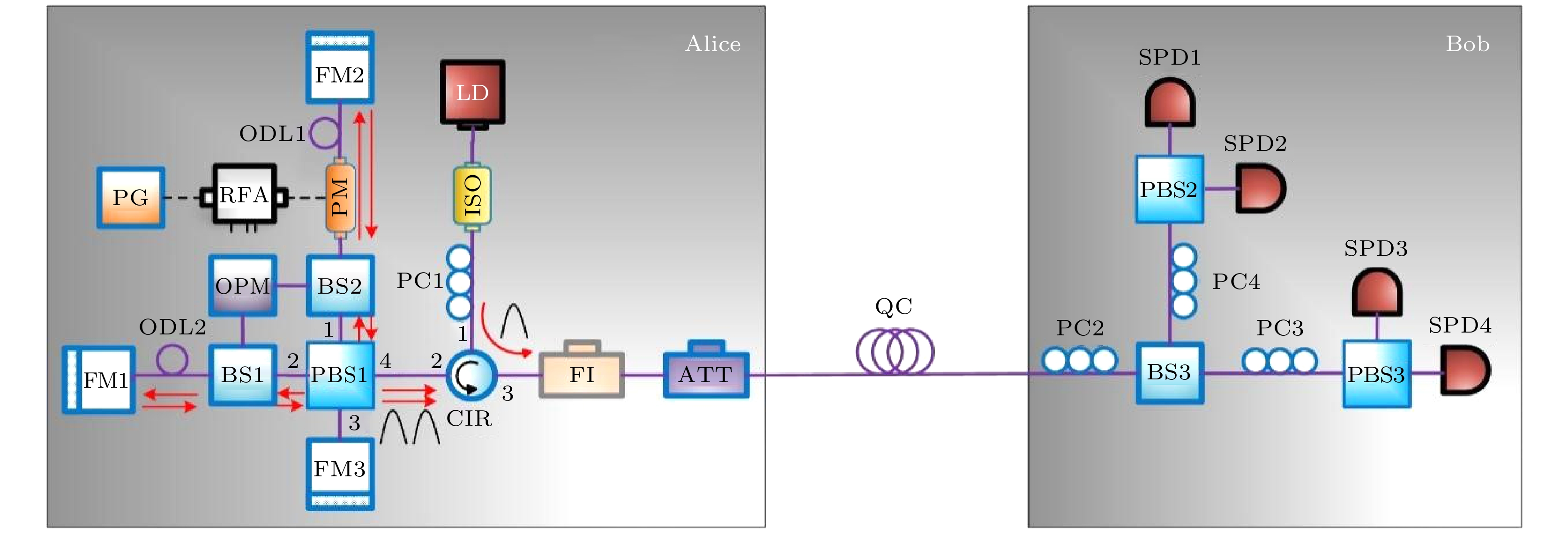
图 4 双向差分调制模式在PMU上的应用, 图中红色箭头表示串扰的方向. LD, 激光二极管; ISO, 隔离器; PC, 偏振控制器; CIR, 光环形器; PBS, 偏振分束器; BS, 分束器; PM, 相位调制器; ODL, 光延迟线; FM, 法拉第镜; OPM, 光功率计; PG, 电脉冲发生器; RFA, 射频放大器; FI, 滤波器; ATT, 衰减器; QC, 量子信道; SPD, 单光子探测器
Figure 4. Application of two-way differential modulation mode to PMU, the red arrow in the figure indicates the direction of crosstalk. LD, laser diode; ISO, isolator; PC, polarization controller; CIR, optical circulator; PBS, polarization beam splitter; BS, beam splitter; PM, phase modulation; ODL, optical delay lines; FM, Faraday mirror; OPM, optical power meter; PG, electrical pulse generator; RFA, radio-frequency amplifier; FI, filter; ATT, attenuator; QC, quantum channel; SPD, single photon detector.
图 5 在PMU双向差分调制模式下, 持续2 h测试得到的
$\left| D \right\rangle $ ,$\left| A \right\rangle $ ,$\left| L \right\rangle $ ,$\left| R \right\rangle $ 四种偏振态的QBER (a) 无扰动情况下的QBER; (b) 200 Hz振动情况下的QBERsFigure 5. Measured QBERs of the four polarization states (
$\left| D \right\rangle, $ $\left| A \right\rangle $ ,$\left| L \right\rangle $ ,$\left| R \right\rangle $ ) for two hours under the two-way differential modulation mode applied to PMU: (a) QBERs in an undisturbed environment; (b) QBERs under a 200 Hz vibration environment. -
[1] Gisin N, Ribordy G, Tittel W, Zbinden H 2001 Rev. Mod. Phys. 74 145
Google Scholar
[2] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[3] Scarani V, Bechmann P H, Cerf N J, Dušek M, Lütkenhaus N, Peev M 2009 Rev. Mod. Phys. 81 1301
Google Scholar
[4] Gobby C, Yuan Z L, Shields A J 2004 Appl. Phys. Lett. 84 37628
Google Scholar
[5] Yin H L, Chen T Y, Yu Z W, Liu H, You L X, Zhou Y H, Chen S J, Mao Y, Huang M Q, Zhang W J, Chen H, Li M J, Nolan D, Zhou F, Jiang X, Wang Z, Zhang Q, Wang X B, Pan J W 2016 Phys. Rev. Lett. 117 190501
Google Scholar
[6] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W, Hu X L, Guan J Y, Yu Z W, Xu H, Lin J 2020 Phys. Rev. Lett. 124 070501
Google Scholar
[7] Wang J Y, Yang B, Liao S K, Zhang L, Shen Q, Hu X F, Wu J C, Yang S J, Jiang H, Tang Y L 2013 Nat. Photonics 7 387
Google Scholar
[8] Nauerth S, Moll F, Rau M, Fuchs C, Horwath J, Frick S, Weinfurter H 2013 Nat. Photonics 7 382
Google Scholar
[9] Liao S K, Cai W Q, Liu W Y, Zhang L, Li Y, Ren J G, Yin J, Shen Q, Cao Y, Li Z P 2017 Nature 549 43
Google Scholar
[10] Hill A D, Chapman J, Herndon K, Chopp C, Gauthier D J, Kwiat P 2017 Urbana 51 61801
Google Scholar
[11] Liu H Y, Tian X H, Gu C, Fan P, Ni X, Yang R, Zhang J N, Hu M, Niu Y, Cao X 2020 Nat. Sci. Rev. 7 921
Google Scholar
[12] Liao S K, Yong H L, Liu C, Shentu G L, Li D D, Lin J, Dai H, Zhao S Q, Li B, Guan J Y 2017 Nat. Photonics 11 509
Google Scholar
[13] Chen H, Wang J, Tang B, Li Z, Sun S H 2020 Opt. Lett. 45 3022
Google Scholar
[14] Xue Y, Shi L, Wei J, Yu L, Yu H, Tang J, Zhang Z 2020 Int. J. Theor. Phys. 59 3299
Google Scholar
[15] Pugh C J, Kaiser S, Bourgoin J P, Jin J, Sultana N, Agne S, Anisimova E, Makarov V, Choi E, Higgins B L 2017 Quantum Sci. Technol. 2 024009
Google Scholar
[16] Bourgoin J P, Higgins B L, Gigov N, Holloway C, Pugh C J, Kaiser S, Cranmer M, Jennewein T 2015 Opt. Express 23 33437
Google Scholar
[17] DeCesare A, Snyder R, Carvalho D, Miller W A, Alsing P M, Ahn D 2020 Proc. SPIE 11391 1139105
Google Scholar
[18] Liu X, Liao C, Tang Z, Wang J, Liu S 2007 Proc. SPIE 6827 682701
Google Scholar
[19] Liu X, Liao C, Mi J, Wang J, Liu S 2008 Phys. Lett. A 373 54
Google Scholar
[20] Lucio-Martinez I, Chan P, Mo X, Hosier S, Tittel W 2009 New J. Phys. 11 095001
Google Scholar
[21] Grunenfelder F, Boaron A, Rusca D, Martin A, Zbinden H 2018 Appl. Phys. Lett. 112 051108
Google Scholar
[22] Li Y, Li Y H, Xie H B, Li Z P, Peng C Z 2019 Opt. Lett. 44 5262
Google Scholar
[23] Agnesi C, Avesani M, Stanco A, Villoresi P, Vallone G 2019 Opt. Lett. 44 2398
Google Scholar
[24] Avesani M, Agnesi C, Stanco A, Vallone G, Villoresi P 2020 Opt. Lett. 45 4706
Google Scholar
[25] Wang J, Qin X, Jiang Y, Wang X, Chen L, Zhao F, Wei Z, Zhang Z 2016 Opt. Express 24 8302
Google Scholar
[26] Yuan Y, Du C, Shen Q, Wang J, Yu Y, Wei Z, Chen Z, Zhang Z 2020 Opt. Express 28 10772
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3812
- PDF Downloads: 71
- Cited By: 0
