-
During directional solidification of binary alloy mixtures, instability in the solid/liquid interface appears due to constitutional undercooling. As a result of this instability, a reactive porous medium, namely mushy layer, is formed, and it separates the liquid phase from the solid phase completely. The intrinsic structure of the mushy layer is of fine-scale dendritic crystal that shelters solute in the interstitial fluid. In a gravitational field, the rejection of lighter solute components from an advancing solidification front brings about unstable density gradient. Ensuing convective motions in the mush are driven by a density difference. The convection can change the solid matrix of the mushy layer. Hence, the dynamic response of the mushy layer is driven by interaction among heat transfer, solute transport and convection. As a contactless control tool, external magnetic field can change the heat and solute transport, which has a significant effect on the phase change process. Therefore, when magnetic field, thermal diffusion, solute transport and buoyancy convection are considered simultaneously in the phase transformation process, the mechanism of mushy region will become more complex and interesting. In this paper, the effect of external magnetic field on the stability of mushy layer during binary alloy solidification is studied. The coupling effects of magnetic field, temperature field, concentration field and convection are considered in the model. Including the direct mode and the oscillation mode, the resulting dispersion relation reveals the influence of magnetic field on the stability of mushy layer through linear stability analysis. It is found that the Lorentz force can reduce the instability effect which is caused by buoyancy convection. In the oscillation mode, an external magnetic field brings about a stabilizing effect on the mushy layer, but in the direct mode, the effect of external magnetic field on stability of the mushy layer is uncertain. In conclusion, the finding in this paper provides an important theoretical reference for improving products quality by applying an external magnetic field in the metals processing industry.
-
Keywords:
- mushy layer /
- magnetohydrodynamics /
- stability
[1] Kurz W, Fisher D J 1989 Fundamentals of Solidification (Aedermannsdorf: Enfield Publishing & Distribution Company) pp46−55
[2] Amberg G, Homsy G M 1993 J. Fluid Mech. 252 79
Google Scholar
[3] Mullins W W, Sekerka R F 1964 J. Appl. Phys. 35 444
Google Scholar
[4] Anderson D M, Guba P 2020 Annu. Rev. Fluid Mech. 52 93
Google Scholar
[5] Anderson D M, Worster M G 1996 J. Fluid Mech. 307 245
Google Scholar
[6] Guba P, Anderson D M 2014 J. Fluid Mech. 760 634
Google Scholar
[7] Ganapathysubramanian B, Zabaras N 2005 Int. J. Heat Mass Transf. 48 4174
Google Scholar
[8] Tian X Y, Zou F, Li B W, He J C 2010 Metall. Mater. Trans. B 40 112
[9] Cukierski K, Thomas B G 2008 Metall. Mater. Trans. B 39 94
Google Scholar
[10] Thomas B G, Zhang L 2001 ISIJ Int. 41 1181
Google Scholar
[11] Mofatt H K 1965 J. Fluid Mech. 22 521
Google Scholar
[12] Saluja N, Ilegbusi O J, Szekely J 1990 J. Appl. Phys. 68 5845
Google Scholar
[13] Kumar A, Dutta P 2005 Int. J. Heat Mass Transf. 48 3674
Google Scholar
[14] Riahi D N 2000 J. Cryst. Growth 216 501
Google Scholar
[15] Muddamallappa M S, Bhatta D, Riahi D N 2009 Transport Porous Med. 79 301
Google Scholar
[16] Kao A, Cai B, Lee P D, Pericleous K 2017 J. Cryst. Growth 457 270
Google Scholar
[17] Sarkar S, Ganguly S, Dutta P 2017 Appl. Math. Model 48 233
Google Scholar
[18] Anderson D M 2003 J. Fluid Mech. 483 165
Google Scholar
[19] Anderson D M, Mcfadden G B, Coriell S R, Murray B T 2010 J. Fluid Mech. 647 309
Google Scholar
[20] Guba P, Anderson D M 2017 J. Fluid Mech. 825 853
Google Scholar
[21] Moreau R J 2013 Magnetohydrodynamics (Vol. 3) (Berlin: Springer Science & Business Media) pp4−12
-
图 1 以恒定速度
${V^*}$ 凝固的糊状层示意图Figure 1. Schematic representation of mushy layer system, which advancing upwards with a constant solidification speed
${V^*}$ .
图 2 直接模式的中性稳定性曲线和不稳定区域(阴影部分)示意图 (a)情况1; (b)情况2; (c)情况3; (d)情况4
Figure 2. Schematic representation of the neutral-stability curves and the regions of instability (shaded) for direct modes: (a) Situation 1; (b) situation 2; (c) situation 3; (d) situation 4.
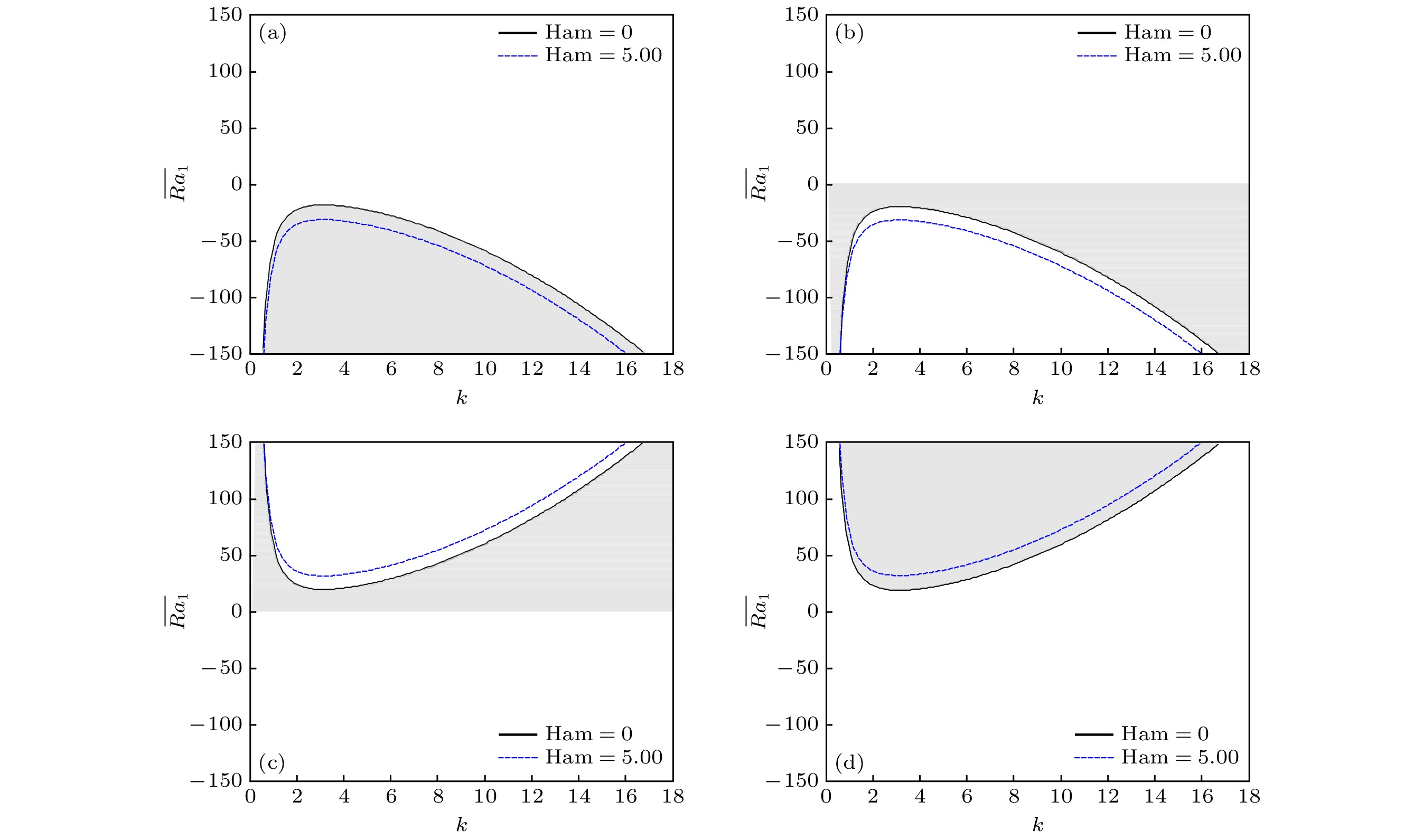
图 3 振荡模式的中性稳定性曲线示意图(振荡模式的不稳定性区域为图中实线(黑色)和点划线(红色)之间的部分) (a)情况1; (b)情况2; (c)情况3; (d)情况4
Figure 3. Schematic representation of the neutral-stability curves for the oscillatory modes: (a) Situation 1; (b) situation 2; (c) situation 3; (d) situation 4. The instability region of oscillation mode is the part between solid line (black) and dashed line (red).
-
[1] Kurz W, Fisher D J 1989 Fundamentals of Solidification (Aedermannsdorf: Enfield Publishing & Distribution Company) pp46−55
[2] Amberg G, Homsy G M 1993 J. Fluid Mech. 252 79
Google Scholar
[3] Mullins W W, Sekerka R F 1964 J. Appl. Phys. 35 444
Google Scholar
[4] Anderson D M, Guba P 2020 Annu. Rev. Fluid Mech. 52 93
Google Scholar
[5] Anderson D M, Worster M G 1996 J. Fluid Mech. 307 245
Google Scholar
[6] Guba P, Anderson D M 2014 J. Fluid Mech. 760 634
Google Scholar
[7] Ganapathysubramanian B, Zabaras N 2005 Int. J. Heat Mass Transf. 48 4174
Google Scholar
[8] Tian X Y, Zou F, Li B W, He J C 2010 Metall. Mater. Trans. B 40 112
[9] Cukierski K, Thomas B G 2008 Metall. Mater. Trans. B 39 94
Google Scholar
[10] Thomas B G, Zhang L 2001 ISIJ Int. 41 1181
Google Scholar
[11] Mofatt H K 1965 J. Fluid Mech. 22 521
Google Scholar
[12] Saluja N, Ilegbusi O J, Szekely J 1990 J. Appl. Phys. 68 5845
Google Scholar
[13] Kumar A, Dutta P 2005 Int. J. Heat Mass Transf. 48 3674
Google Scholar
[14] Riahi D N 2000 J. Cryst. Growth 216 501
Google Scholar
[15] Muddamallappa M S, Bhatta D, Riahi D N 2009 Transport Porous Med. 79 301
Google Scholar
[16] Kao A, Cai B, Lee P D, Pericleous K 2017 J. Cryst. Growth 457 270
Google Scholar
[17] Sarkar S, Ganguly S, Dutta P 2017 Appl. Math. Model 48 233
Google Scholar
[18] Anderson D M 2003 J. Fluid Mech. 483 165
Google Scholar
[19] Anderson D M, Mcfadden G B, Coriell S R, Murray B T 2010 J. Fluid Mech. 647 309
Google Scholar
[20] Guba P, Anderson D M 2017 J. Fluid Mech. 825 853
Google Scholar
[21] Moreau R J 2013 Magnetohydrodynamics (Vol. 3) (Berlin: Springer Science & Business Media) pp4−12
DownLoad:
Catalog
Metrics
- Abstract views: 4539
- PDF Downloads: 41
- Cited By: 0
