-
In the Su-Schrieffer-Heeger (SSH) chain, the nontrivial topological edge states will have different winding numbers when the intra-cell and inter-cell hopping amplitudes are spin-dependent ones. Consequently, how to detect the edge states with different winding numbers theoretically and experimentally has become one of important topics in condensed matter physics. In this paper, in the framework of the tight-binding approximation, we study the topological properties and the electron transport properties of the edge states of the SSH chain with the spin-orbit coupling. It is demonstrated that the winding numbers of the quadruple-degenerate and twofold-degenerate edge states are two and one, respectively. Importantly, the electron transport properties in the vicinity of the zero energy can characterize the energy spectra of the edge states, when the spin-polarized electrons tunnel into the SSH chain from the source lead, namely, the source lead is a ferromagnetic one. With increasing the tunneling coupling strengths between the SSH chain and the two leads from the weak coupling regime to the strong coupling one, the number of transmission resonance peaks of the quadruple-degenerate with the winding numbers being two and twofold-degenerate edge states with the winding numbers being one will be reduced by four and two, respectively. In other words, the transmission resonance peaks related to the edge states will disappear when the SSH chain is strongly coupled to the two leads. Therefore, these results suggest an alternative way of detecting the nontrivial topological ones with different winding numbers by changing the number of transmission resonance peaks of edge states.
[1] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[2] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[3] Saei Ghareh Naz E, FulgaI I C, Ma L, Schmidt O G, van den Brink J 2018 Phys. Rev. A 98 033830
Google Scholar
[4] Wang Y, Lu Y H, Mei F, Gao J, Li Z M, Tang H, Zhu S L, Jia S T, Jin X M 2019 Phys. Rev. Lett. 122 193903
Google Scholar
[5] Atala M, Aidelsburger M, Barreiro J T, Abanin D, Kitagawa T, Demler E, Bloch I 2013 Nat. Phys. 9 795
Google Scholar
[6] Xie D Z, Gou W, Xiao T, Gadway B, Yan B 2019 NPJ Quantum Inf. 5 55
Google Scholar
[7] Drost R, Ojanen T, Harju A, Liljeroth P 2017 Nat. Phys. 13 668
Google Scholar
[8] Huda M N, Kezilebieke S, Ojanen T, Drost R, Liljeroth P 2020 NPJ Quantum Mater. 5 17
Google Scholar
[9] Poshakinskiy A V, Poddubny A N, Hafezi M 2015 Phys. Rev. A 91 043830
Google Scholar
[10] Hafezi M 2014 Phys. Rev. Lett. 112 210405
Google Scholar
[11] Petráček J, Kuzmiak V 2020 Phys. Rev. A 101 033805
Google Scholar
[12] Dong B, Lei X L 2018 Ann. Phys. 396 245
Google Scholar
[13] Böhling S, Engelhardt G, Platero G, Schaller G 2018 Phys. Rev. B 98 035132
Google Scholar
[14] 张蓝云, 薛海斌, 陈彬, 陈建宾, 邢丽丽 2020 69 077301
Google Scholar
Zhang L Y, Xue H B, Chen B, Chen J B, Xing L L 2020 Acta Phys. Sin. 69 077301
Google Scholar
[15] Tewari S, Sau D J 2012 Phys. Rev. Lett. 109 150408
Google Scholar
[16] Manchon A, Koo H C, Nitta J, Frolov S M, Duine R A 2015 Nat. Mater. 14 871
Google Scholar
[17] Lin Y J, Jiménez-García K, Spielman I B 2011 Nature 471 83
Google Scholar
[18] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[19] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[20] Galitski V, Spielman I B 2013 Nature 494 49
Google Scholar
[21] Whittaker C E, Cancellieri E, Walker P M, Royall B, Rodriguez L E T, Clarke E, Whittaker D M, Schomerus H, Skolnick M S, Krizhanovskii D N 2019 Phys. Rev. B 99 081402(R
Google Scholar
[22] Bahari M, Hosseini M V 2016 Phys. Rev. B 94 125119
Google Scholar
[23] Yao Y, Sato M, Nakamura T, Furukawa N, Oshikawa M 2017 Phys. Rev. B 96 205424
Google Scholar
[24] Ahmadi N, Abouie J, Baeriswyl D 2020 Phys. Rev. B 101 195117
Google Scholar
[25] Bahari M, Hosseini M V 2020 Physica E 119 113973
Google Scholar
[26] Asbóth J K, Oroszlány L, Pályi A 2016 A Short Course on Topological Insulators (Budapest: Springer) pp1−44
[27] Shen S Q 2017 Topological Insulators 2 nd ed. (Singapore: Springer) pp51−79
[28] Wakatsuki R, Ezawa M, Tanaka Y, Nagaosa N 2014 Phys. Rev. B 90 014505
Google Scholar
-
图 1 自旋轨道耦合SSH原子链与左、右导线耦合系统的示意图. 其中, 红色实心圆表示A原子, 蓝色实心圆表示B原子, 黑色空心圆表示导线上的原子.
${t_0}$ 表示导线上相邻原子之间的跳跃振幅,${t_{{\rm{L}}, \sigma }}$ 和${t_{{\rm{R}}, \sigma }}$ 表示自旋轨道耦合SSH原子链与左、右电极之间自旋依赖的隧穿耦合强度.$\upsilon $ 和w分别表示胞内和胞间自旋守恒的跳跃振幅, 而${\lambda _{\upsilon} }$ 和${\lambda _w}$ 则分别表示胞内和胞间自旋翻转的跳跃振幅Figure 1. The schematic diagram of the SSH chain with spin-orbit coupling coupled to the left and right leads. The red filled circles denote the A atoms, the blue filled circles denote the B atoms, the black unfilled circles denote atoms on the leads.
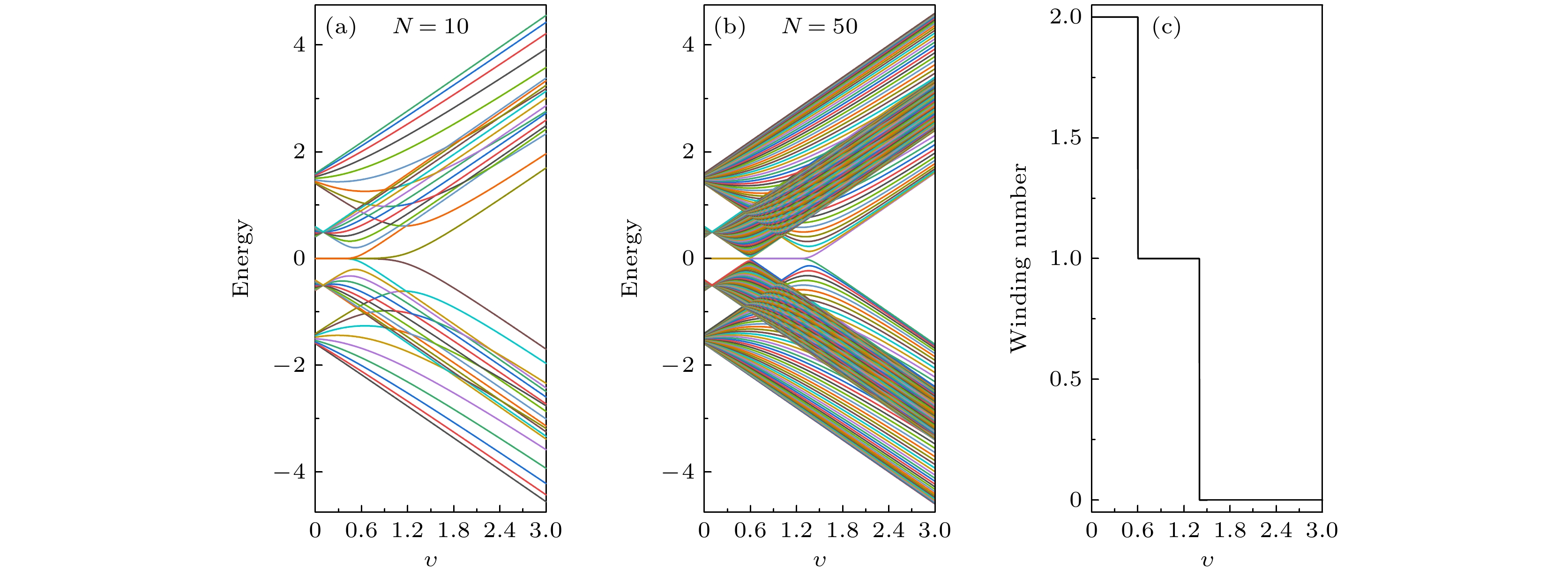
${t_0}$ describes the hopping amplitude between two adjacent atoms on the leads.${t_{{\rm{L}}, \sigma }}$ and${t_{{\rm{R}}, \sigma }}$ characterize the spin-dependent tunnel coupling strengths between the SSH chain with spin-orbit coupling and the left lead, and that between the SSH chain with spin-orbit coupling and the right lead, respectively.$\upsilon $ and w are the intra-cell and inter-cell hopping amplitudes with the spin-conserving processes, respectively. Whereas${\lambda _{\upsilon} }$ and${\lambda _w}$ are the intra-cell and inter-cell hopping amplitudes with the spin-flip processes, respectively
图 2 (a) 原胞数目为10的自旋轨道耦合SSH原子链的能谱图; (b) 原胞数目为50的自旋轨道耦合SSH原子链的能谱图; (c) 自旋轨道耦合SSH原子链的缠绕数随着胞内自旋守恒跳跃振幅
$\upsilon $ 的变化图. 自旋轨道耦合SSH原子链的参数选取为:$w = 1.0$ ,${\lambda _{\upsilon} } = 0.1$ 和${\lambda _w} = 0.5$ Figure 2. (a), (b) The energy spectrum of the SSH chain with spin-orbit coupling for
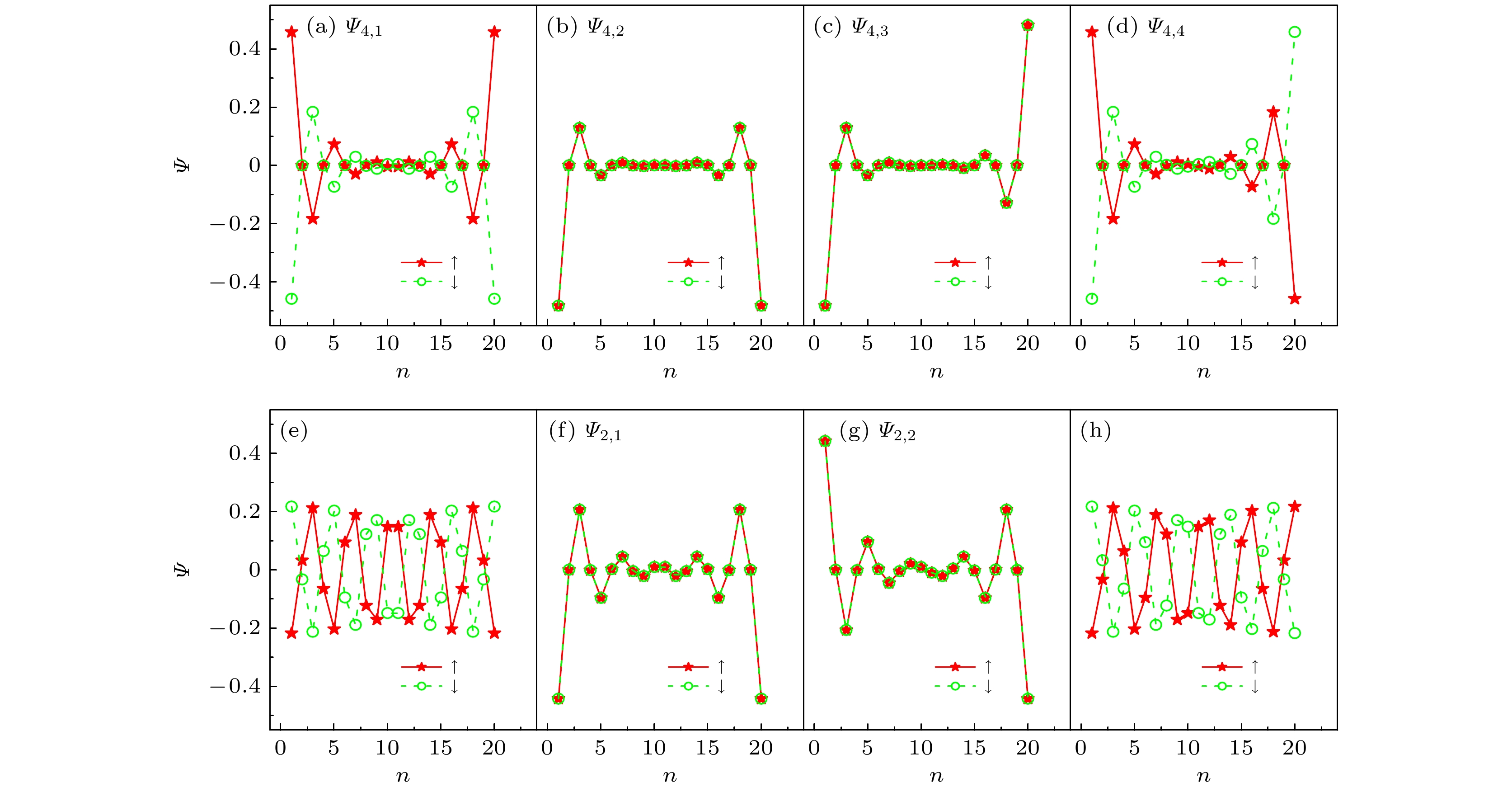
$N = 10$ and$N = 50$ , respectively; (c) the winding number of the SSH chain with spin-orbit coupling as a function of the intra-cell hopping amplitude with the spin-conserving process$\upsilon $ . The parameters of the SSH chain with spin-orbit coupling are chosen as$w = 1.0$ ,${\lambda _{\upsilon} } = 0.1$ and${\lambda _w} = 0.5$ .
图 3 自旋轨道耦合SSH原子链的本征值在4个零能附近的本征态波函数在每个原子上的几率幅分布图 (a)—(d)
$ \upsilon = 0.3$ ; (e)—(h)$ \upsilon = 0.6$ , 自旋轨道耦合SSH原子链的其他参数选取为$ w = 1.0$ ,$ {\lambda _\upsilon } = 0.1$ ,$ {\lambda _w} = 0.5$ ,$ N = 10$ Figure 3. (a)–(d) The distribution of probability amplitudes of the wave functions of the four nearly zero-energy eigenstates of the SSH chain with spin-orbit coupling: (a)–(d)
$\upsilon = 0.3$ ; (e)–(h)$\upsilon = 0.6$ . The other parameters of the SSH chain with spin-orbit coupling are chosen as$w = 1.0$ ,${\lambda _{\upsilon} } = 0.1$ ,${\lambda _w} = 0.5$ and$N = 10$ .
图 4 自旋轨道耦合SSH原子链的电子透射率在不同自旋极化率情形下随入射电子能量的变化 (a)
$\upsilon = 0.3$ ; (b)$\upsilon = $ $ 0.6$ , 其他参数与图3相同Figure 4. The transmission probabilities of the SSH chain with spin-orbit coupling as a function of the energy of incident electron for the different spin polarizations of left lead: (a)
$\upsilon = $ $ 0.3$ ; (b)$\upsilon = 0.6$ . The other parameters are the same as Fig. 3.
图 5 (a), (b) 自旋轨道耦合SSH原子链在零能级附近的能谱图; (c) 自旋轨道耦合SSH原子链与左导线原子
$j = - 1$ , 右导线原子$j = 1$ 耦合的系统在零能级附近的能谱图,${t_{\rm{L}}} = {t_{\rm{R}}} = 0.1$ , 其他参数与图3相同.Figure 5. (a) and (b) Energy spectrum of the SSH chain with spin-orbit coupling in the vicinity of the zero energy; (c) energy spectrum of the SSH chain with spin-orbit coupling coupled to the atom of the left lead
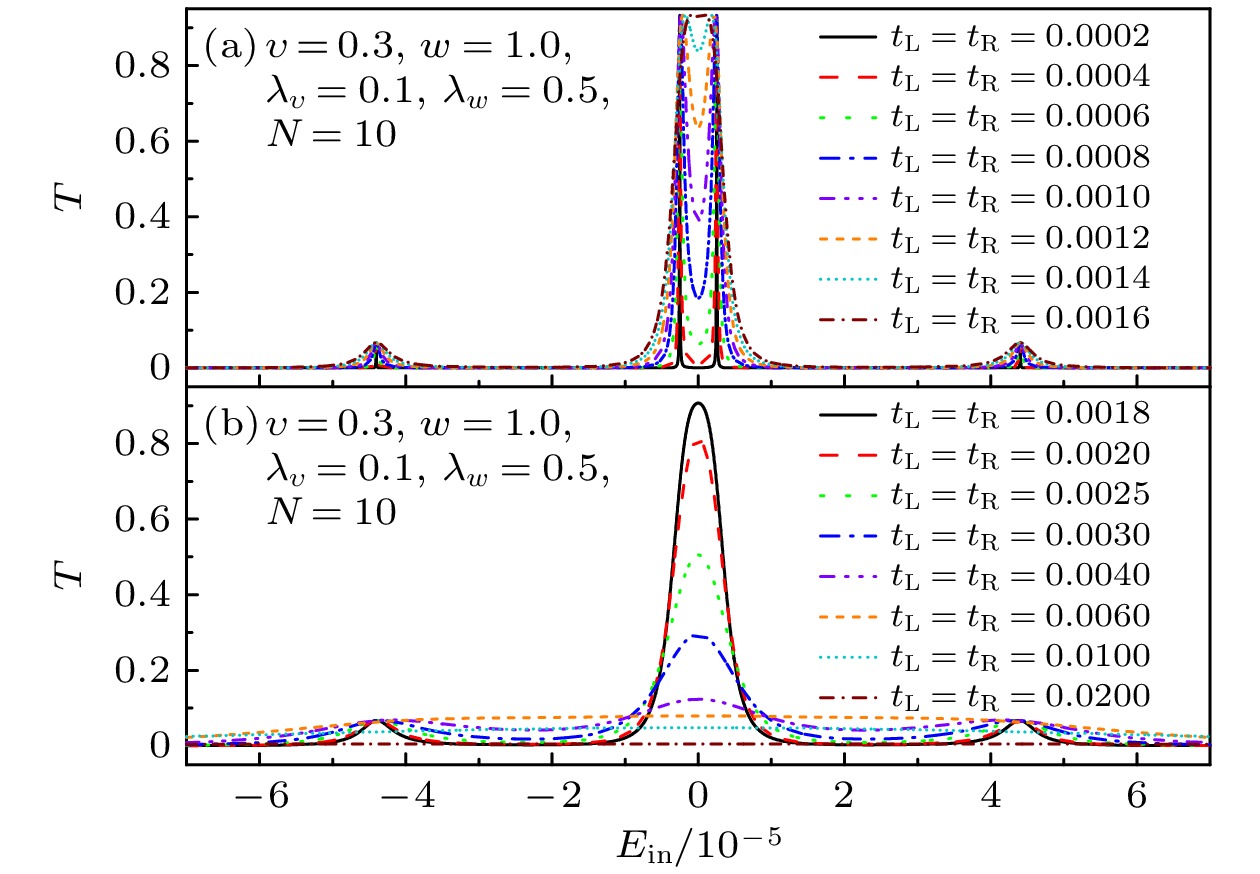
$j = - 1$ and that of the right lead$j = 1$ in the vicinity of the zero energy, where${t_{\rm{L}}} = {t_{\rm{R}}} = 0.1$ . The other parameters are the same as Fig. 3
图 6 自旋轨道耦合SSH原子链的电子透射率在不同隧穿耦合强度下随入射电子能量的变化,
$\upsilon = 0.3$ , 其他参数与图3相同Figure 6. The transmission probabilities of the SSH chain with spin-orbit coupling as a function of the energy of incident electron for different strengths of tunneling coupling,
$\upsilon = 0.3$ . The other parameters are the same as Fig. 3.
图 7 自旋轨道耦合SSH原子链的电子透射率在不同隧穿耦合强度下随入射电子能量的变化,
$\upsilon = 0.6$ , 其他参数与图3相同Figure 7. The transmission probabilities of the SSH chain with spin-orbit coupling as a function of the energy of incident electron for different strengths of tunneling coupling,
$\upsilon = 0.6$ . The other parameters are the same as Fig. 3. -
[1] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[2] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[3] Saei Ghareh Naz E, FulgaI I C, Ma L, Schmidt O G, van den Brink J 2018 Phys. Rev. A 98 033830
Google Scholar
[4] Wang Y, Lu Y H, Mei F, Gao J, Li Z M, Tang H, Zhu S L, Jia S T, Jin X M 2019 Phys. Rev. Lett. 122 193903
Google Scholar
[5] Atala M, Aidelsburger M, Barreiro J T, Abanin D, Kitagawa T, Demler E, Bloch I 2013 Nat. Phys. 9 795
Google Scholar
[6] Xie D Z, Gou W, Xiao T, Gadway B, Yan B 2019 NPJ Quantum Inf. 5 55
Google Scholar
[7] Drost R, Ojanen T, Harju A, Liljeroth P 2017 Nat. Phys. 13 668
Google Scholar
[8] Huda M N, Kezilebieke S, Ojanen T, Drost R, Liljeroth P 2020 NPJ Quantum Mater. 5 17
Google Scholar
[9] Poshakinskiy A V, Poddubny A N, Hafezi M 2015 Phys. Rev. A 91 043830
Google Scholar
[10] Hafezi M 2014 Phys. Rev. Lett. 112 210405
Google Scholar
[11] Petráček J, Kuzmiak V 2020 Phys. Rev. A 101 033805
Google Scholar
[12] Dong B, Lei X L 2018 Ann. Phys. 396 245
Google Scholar
[13] Böhling S, Engelhardt G, Platero G, Schaller G 2018 Phys. Rev. B 98 035132
Google Scholar
[14] 张蓝云, 薛海斌, 陈彬, 陈建宾, 邢丽丽 2020 69 077301
Google Scholar
Zhang L Y, Xue H B, Chen B, Chen J B, Xing L L 2020 Acta Phys. Sin. 69 077301
Google Scholar
[15] Tewari S, Sau D J 2012 Phys. Rev. Lett. 109 150408
Google Scholar
[16] Manchon A, Koo H C, Nitta J, Frolov S M, Duine R A 2015 Nat. Mater. 14 871
Google Scholar
[17] Lin Y J, Jiménez-García K, Spielman I B 2011 Nature 471 83
Google Scholar
[18] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[19] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[20] Galitski V, Spielman I B 2013 Nature 494 49
Google Scholar
[21] Whittaker C E, Cancellieri E, Walker P M, Royall B, Rodriguez L E T, Clarke E, Whittaker D M, Schomerus H, Skolnick M S, Krizhanovskii D N 2019 Phys. Rev. B 99 081402(R
Google Scholar
[22] Bahari M, Hosseini M V 2016 Phys. Rev. B 94 125119
Google Scholar
[23] Yao Y, Sato M, Nakamura T, Furukawa N, Oshikawa M 2017 Phys. Rev. B 96 205424
Google Scholar
[24] Ahmadi N, Abouie J, Baeriswyl D 2020 Phys. Rev. B 101 195117
Google Scholar
[25] Bahari M, Hosseini M V 2020 Physica E 119 113973
Google Scholar
[26] Asbóth J K, Oroszlány L, Pályi A 2016 A Short Course on Topological Insulators (Budapest: Springer) pp1−44
[27] Shen S Q 2017 Topological Insulators 2 nd ed. (Singapore: Springer) pp51−79
[28] Wakatsuki R, Ezawa M, Tanaka Y, Nagaosa N 2014 Phys. Rev. B 90 014505
Google Scholar
-
[1] Yang Yan-Li, Duan Zhi-Lei, Xue Hai-Bin. Edge states and skin effect dependent electron transport properties of non-Hermitian Su-Schrieffer-Heeger chain. Acta Physica Sinica, 2023, 72(24): 247301. doi: 10.7498/aps.72.20231286 [2] Xia Qun, Deng Wen-Ji. Conductance peaks of bulk states and edge states. Acta Physica Sinica, 2022, 71(13): 137301. doi: 10.7498/aps.71.20212424 [3] Wang Zhi-Mei, Wang Hong, Xue Nai-Tao, Cheng Gao-Yan. Quantum coherence in spin-orbit coupled quantum dots system. Acta Physica Sinica, 2022, 71(7): 078502. doi: 10.7498/aps.71.20212111 [4] Li Jia-Rui, Wang Zi-An, Xu Tong-Tong, Zhang Lian-Lian, Gong Wei-Jiang. Topological properties of the one-dimensional ${\cal {PT}}$ -symmetric non-Hermitian spin-orbit-coupled Su-Schrieffer-Heeger model. Acta Physica Sinica, 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796[5] Shi Ting-Ting, Wang Liu-Jiu, Wang Jing-Kun, Zhang Wei. Some recent progresses on the study of ultracold quantum gases with spin-orbit coupling. Acta Physica Sinica, 2020, 69(1): 016701. doi: 10.7498/aps.69.20191241 [6] Zhang Lan-Yun, Xue Hai-Bin, Chen Bin, Chen Jian-Bin, Xing Li-Li. Electron transport through a quantum-dot-Su-Schrieffer-Heeger-chain system. Acta Physica Sinica, 2020, 69(7): 077301. doi: 10.7498/aps.69.20191871 [7] Li Zhi-Qiang, Wang Yue-Ming. One-dimensional spin-orbit coupling Bose gases with harmonic trapping. Acta Physica Sinica, 2019, 68(17): 173201. doi: 10.7498/aps.68.20190143 [8] Zhang Wei-Feng, Li Chun-Yan, Chen Xian-Feng, Huang Chang-Ming, Ye Fang-Wei. Topological zero-energy modes in time-reversal-symmetry-broken systems. Acta Physica Sinica, 2017, 66(22): 220201. doi: 10.7498/aps.66.220201 [9] Gong Shi-Jing, Duan Chun-Gang. Recent progress in Rashba spin orbit coupling on metal surface. Acta Physica Sinica, 2015, 64(18): 187103. doi: 10.7498/aps.64.187103 [10] Wang Qing, Sheng Li. Edge mode of InAs/GaSb quantum spin hall insulator in magnetic field. Acta Physica Sinica, 2015, 64(9): 097302. doi: 10.7498/aps.64.097302 [11] Meng Zeng-Ming, Huang Liang-Hui, Peng Peng, Chen Liang-Chao, Fan Hao, Wang Peng-Jun, Zhang Jing. Raman coupling in atomic Bose-Einstein condensed with phase-locked laser system. Acta Physica Sinica, 2015, 64(24): 243202. doi: 10.7498/aps.64.243202 [12] Li Gui-Xia, Jiang Yong-Chao, Ling Cui-Cui, Ma Hong-Zhang, Li Peng. The characteristics of excited states for HF+ ion under spin-orbit coupling. Acta Physica Sinica, 2014, 63(12): 127102. doi: 10.7498/aps.63.127102 [13] Tang Nai-Yun. Bonding-antibonding ground state transition in coupled quantum dots. Acta Physica Sinica, 2013, 62(5): 057301. doi: 10.7498/aps.62.057301 [14] Wu Shao-Quan, Chen Jia-Feng, Zhao Guo-Ping. The effect of the interdot Coulomb interaction on Kondo resonance in series-coupled double quantum dots. Acta Physica Sinica, 2012, 61(8): 087203. doi: 10.7498/aps.61.087203 [15] Zhang Lei, Li Hui-Wu, Hu Liang-Bin. Study of stability of persistent spin helix in two-dimensional electron gases with spin-orbit coupling. Acta Physica Sinica, 2012, 61(17): 177203. doi: 10.7498/aps.61.177203 [16] Yu Zhi-Qiang, Xie Quan, Xiao Qing-Quan. Effects of the spin-orbit coupling on X-ray spectrum in special relativity. Acta Physica Sinica, 2010, 59(2): 925-931. doi: 10.7498/aps.59.925 [17] Du Xiao-Yu, Zheng Wan-Hua, Ren Gang, Wang Ke, Xing Ming-Xin, Chen Liang-Hui. Slow wave effect of 2-D photonic crystal coupled cavity array. Acta Physica Sinica, 2008, 57(1): 571-575. doi: 10.7498/aps.57.571 [18] Meng Xian-Lan, Gao Xu-Tuan, Qu Zhen, Kang Da-Wei, Liu De-Sheng, Xie Shi-Jie. Effects of interfacial couplings on charge transport properties of DNA molecule. Acta Physica Sinica, 2008, 57(8): 5316-5322. doi: 10.7498/aps.57.5316 [19] Du Juan, Zhang Chun-Min, Zhao Bao-Chang, Sun Yao. Analysis of the transmittance of modified Savart polariscope in the static large field of view polarization interference imaging spectrometer. Acta Physica Sinica, 2008, 57(10): 6311-6318. doi: 10.7498/aps.57.6311 [20] Peng Zhi-Hong, Zhang Chun-Min, Zhao Bao-Chang, Li Ying-Cai, Wu Fu-Quan. The transmittance of Savart polariscope in polarization interference imaging spectrometer. Acta Physica Sinica, 2006, 55(12): 6374-6381. doi: 10.7498/aps.55.6374
DownLoad:
Catalog
Metrics
- Abstract views: 6463
- PDF Downloads: 203
- Cited By: 0
