-
量子光学中的Rabi模型描述了一个与量子谐振子耦合的两能级系统, 当耦合强度与振子频率相当时, 会产生丰富的物理现象. 本文研究了谐波势阱中具有拉曼诱导自旋轨道耦合的Bose气体, 通过将受限系统映射为Rabi模型, 引入量子光学中的平移Fock态利用变分方法求解了系统的本征能态和基态, 发现左右平移Fock态的奇宇称叠加态能量低于平移态的能量，并分别研究了粒子在动量和坐标空间的动力学Zitterbewegung振荡特性以及原子极化的动力学, 给出了一个直观清晰的物理图像, 与相关实验的结果定性一致. 本文的研究结果有助于进一步研究量子光学领域目前难以实现的深度强耦合参数区域的量子Rabi模型, 对冷原子物理的研究也有一些借鉴和启发.
-
关键词:
- Rabi模型 /
- 自旋轨道耦合 /
- Zitterbewegung振荡 /
- 平移Fock态 /
- 变分法
Rabi model is a popular model in quantum optics and describes a two-level system coupling to a quantum resonator. The fruitful physics appears when the coupling strength is comparable to the frequency of the resonator. We investigate the Bose gases of Raman induced spin-orbit coupling with an external harmonic trapping. Using the displacement Fock state in quantum optics we seek for an approximate ground state. We find the superposition state of left and right displaced oscillator state with odd parity has lower energy than the displaced state itself. Besides, we study the time evolution of both the momentum and the position of the system at single particle level to demonstrate the Zitterbewegung oscillating characteristics, which present an intuitive physical picture and are in qualitative agreement with the relevant experimental results. The results are useful to study the Rabi model in deep-strong coupling regime, the model that is difficult to realize in today’s experiment based on the high controllability property of laser, and these results are also instructive for the cold atom physics field.-
Keywords:
- Rabi model /
- spin-orbit coupling /
- Zitterbewegung oscillations /
- displacement Fock state /
- variational method
[1] Xiao D, Chang M C, Niu Q 2010 Rev. Mod. Phys. 82 1959
Google Scholar
[2] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[3] Zutic I, Fabian J, Sarma S D 2004 Rev. Mod. Phys. 76 323
Google Scholar
[4] Lin Y J, Garcıa K J, Spielman I B 2011 Nature 471 8386
[5] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[6] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[7] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[8] Galitski V, Spielman I B 2013 Nature 494 4954
[9] Lin Y J, Compton R L, Garcia K J, Porto J V, Spielman I B 2009 Nature 462 628
Google Scholar
[10] Lin Y J, Compton R L, Perry A R, Phillips W D, Porto J V, Spielman I B 2009 Phys. Rev. Lett. 102 130401
Google Scholar
[11] Qu C, Hamner C, Gong M, Zhang C, Engels P 2013 Phys. Rev. A 88 021604
Google Scholar
[12] LeBlanc L J, Beeler M C, Jimenez-Garcia K, Perry A R, Sugawa S, Williams R A, Spielman I B 2013 New J. Phys. 15 073011
Google Scholar
[13] Wu C J, Mondragon-Shem I, Zhou X F 2011 Chin. Phys. Lett. 28 097102
Google Scholar
[14] Hu H, Ramachandhran B, Pu H, Liu X J 2012 Phys. Rev. Lett. 108 010402
Google Scholar
[15] Sinha S, Nath R, Santos L 2011 Phys. Rev. Lett. 107 270401
Google Scholar
[16] Ghosh S K, Vyasanakere J P, Shenoy V B, 2011 Phys. Rev. A 84 053629
Google Scholar
[17] Larson J, Anderson B M, Altland A 2013 Phys. Rev. A 87 013624
Google Scholar
[18] Rabi I I 1936 Phys. Rev. 49 324
Google Scholar
[19] Rabi I I 1937 Phys. Rev. 51 652
Google Scholar
[20] Braak D 2011 Phys. Rev. Lett. 107 100401
Google Scholar
[21] Chen Q H, Wang C, He S, Liu T, Wang K L 2012 Phys. Rev. A 86 023822
Google Scholar
[22] Solano E 2011 Physics 4 68
Google Scholar
[23] Gardas, Dajka J 2013 arXiv: 1301.5660[quant-ph]
[24] Wolf F A, Kollar M, Braak D 2012 Phys. Rev. A 85 053817
Google Scholar
[25] Walther H, Varcoe B, Englert B, Becker T 2006 Rep. Prog. Phys. 69 1325
Google Scholar
[26] Raimond J M, Brune M, Haroche S 2001 Rev. Mod. Phys. 73 565
Google Scholar
[27] Holstein T 1959 Ann. Phys. 8 325
Google Scholar
[28] Mabuchi H, Doherty A C 2002 Science 298 1372
Google Scholar
[29] Niemczyk T, Deppe F, Huebl H, Menzel E P, Hocke F, Schwarz M J, Garcia-Ripoll J J, Zueco D, Hümmer T, Solano E, Marx A, Gross R 2010 Nature Phys. 6 772
Google Scholar
[30] Forn-Diaz P, Lisenfeld J, Marcos D, Garcia-Ripoll J J, Solano E, Harmans C J P M, Mooij J E 2010 Phys. Rev. Lett. 105 237001
Google Scholar
[31] Fu Z, Wang P, Chai S, Huang L, Zhang J 2011 Phys. Rev. A 84 043609
Google Scholar
[32] Cahill K K, Glauber R J 1969 Phys. Rev. 177 1857
Google Scholar
[33] Graham R, Hohnerbach M 1984 Phys. B: Condens. Matter 57 233
Google Scholar
-
图 1 简并量子态
$\left| {{\psi _{N{\rm{,L}}\left( {\rm{R}} \right)}}} \right\rangle $ 能量${E_{N,{\rm{L/R}}}}$ 与左右平移奇宇称叠加态$\left| {{\psi _{ - ,N}}} \right\rangle $ 能量${E_{ - ,N}}$ 随SO耦合强度$\lambda $ 的变化 可见$N = 0$ 叠加态$\left| {{\psi _{ - ,0}}} \right\rangle $ 能量最低, 更接近基态; 而对于激发态$N \ne 0$ , 二者能量随参数变化出现交叉; 相关参数取值为$\varOmega \; = \;{\rm{1}}{\rm{.4}}\omega $ , 与文献[19]精确解的结果基本一致Fig. 1. The energies of degenerate quantum states
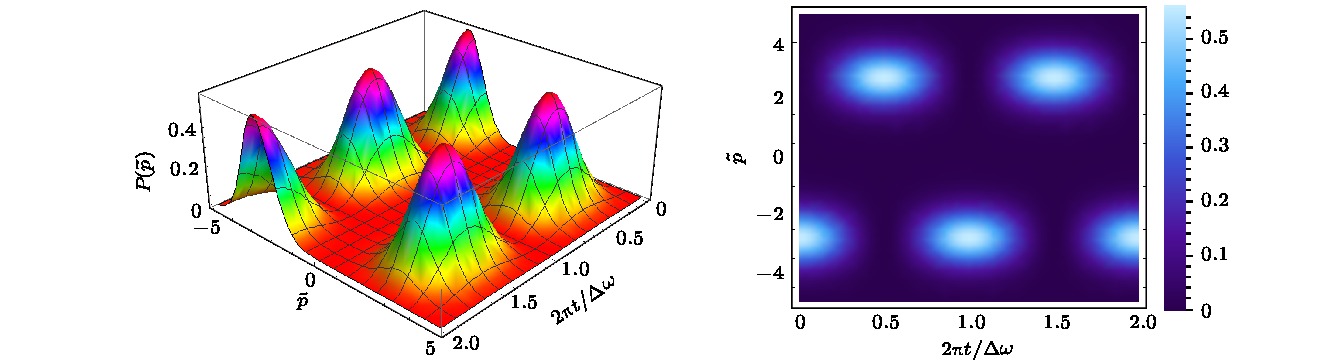
$\left| {{\psi _{N{\rm{,L}}\left( {\rm{R}} \right)}}} \right\rangle $ and the superposition state of odd parity$\left| {{\psi _{ - ,N}}} \right\rangle $ of left(right)-displaced number states varies as the spin-orbit coupling strength$\lambda $ . It is seen that for$N = 0$ , the superposition state has the lowest energy which is the best approximation for the ground state in our interest. And for the cases of$N \ne 0$ , the energies of the two quantum states have pitchforks.The relevant parameters is Ω=1.4 and the results are in agreement with those in Ref.[19].
图 2 原子动量分布概率的粗粒动力学演化 (3D, 左侧; 2D, 右侧) 相关参数取值为
$\varOmega \; = \;{\rm{3}}\omega $ ,$ \lambda \; = \;{\rm{2}}\omega $ , 初态为$\varPsi (t = 0) = {\psi _{0,{\rm L}}}$ , 动量$ \tilde p = \sqrt {1/m\hbar \omega } p $ Fig. 2. The coarse dynamics evulution of momentum distribution of single particle (left for 3D; right for 2D) with
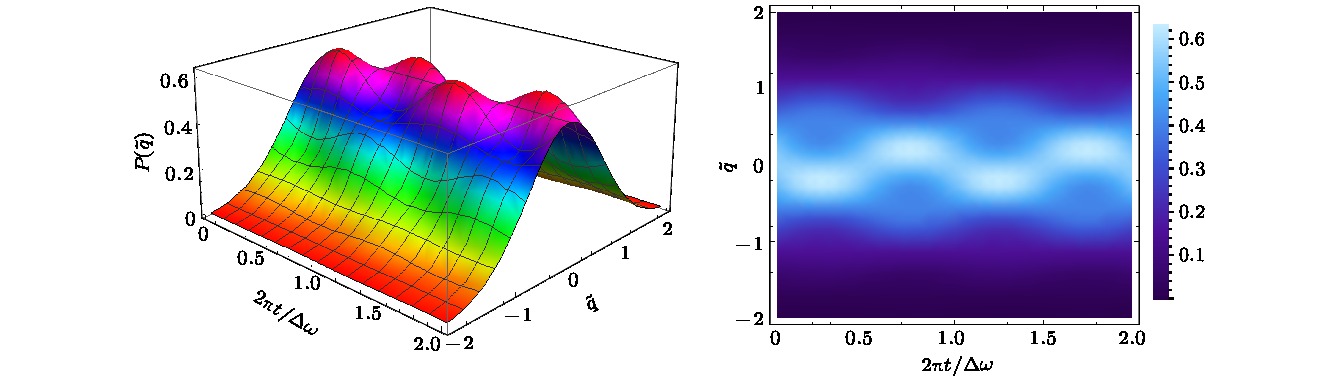
$\varOmega \; = \;{\rm{3}}\omega $ and$ \lambda \; = \;{\rm{2}}\omega $ . The initial state is set as$\varPsi (t = 0) = {\psi _{0,{\rm{L}}}}$ . Momentum$\tilde p$ is defined by$ \tilde p = \sqrt {1/m\hbar \omega } p $ .
图 3 原子空间位置分布概率的粗粒动力学演化(3D, 左侧; 2D, 右侧) 相关参数取值及初态同图2, 位置
$ \tilde q = \sqrt {m\omega /\hbar } q $ Fig. 3. The coarse dynamics evolution of position distribution of single particle (left for 3D; right for 2D) with the same parameters and the initial state in Fig. 2 and
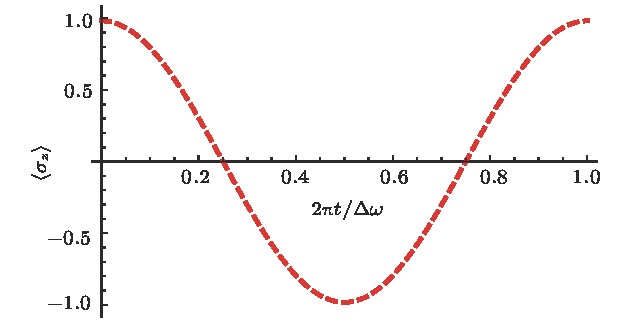
$ \tilde q = \sqrt {m\omega /\hbar } q $ .
图 4 原子极化
$\left\langle {{\sigma _z}} \right\rangle $ 随时间演化初态为$\varPsi \left( {t = 0} \right) = {\psi _{0,{\rm{L}}}}$ , 参数取值为$\varOmega \; = \;{\rm{3}}\omega $ 和$ \lambda \; = \;{\rm{2}}\omega $ , 时间以因子${{2{\text{π}}}/{\Delta \omega }}$ 标度Fig. 4. Time evolution of
$\left\langle {{\sigma _z}} \right\rangle $ with the initial state being$\varPsi \left( {t = 0} \right) = {\psi _{0,{\rm{L}}}}$ and the parameters$\varOmega \; = \;{\rm{3}}\omega $ and$ \lambda \; = \;{\rm{2}}\omega $ . The time is scaled by the tunneling period$2{\text{π}}/\Delta\omega $ . -
[1] Xiao D, Chang M C, Niu Q 2010 Rev. Mod. Phys. 82 1959
Google Scholar
[2] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[3] Zutic I, Fabian J, Sarma S D 2004 Rev. Mod. Phys. 76 323
Google Scholar
[4] Lin Y J, Garcıa K J, Spielman I B 2011 Nature 471 8386
[5] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[6] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[7] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[8] Galitski V, Spielman I B 2013 Nature 494 4954
[9] Lin Y J, Compton R L, Garcia K J, Porto J V, Spielman I B 2009 Nature 462 628
Google Scholar
[10] Lin Y J, Compton R L, Perry A R, Phillips W D, Porto J V, Spielman I B 2009 Phys. Rev. Lett. 102 130401
Google Scholar
[11] Qu C, Hamner C, Gong M, Zhang C, Engels P 2013 Phys. Rev. A 88 021604
Google Scholar
[12] LeBlanc L J, Beeler M C, Jimenez-Garcia K, Perry A R, Sugawa S, Williams R A, Spielman I B 2013 New J. Phys. 15 073011
Google Scholar
[13] Wu C J, Mondragon-Shem I, Zhou X F 2011 Chin. Phys. Lett. 28 097102
Google Scholar
[14] Hu H, Ramachandhran B, Pu H, Liu X J 2012 Phys. Rev. Lett. 108 010402
Google Scholar
[15] Sinha S, Nath R, Santos L 2011 Phys. Rev. Lett. 107 270401
Google Scholar
[16] Ghosh S K, Vyasanakere J P, Shenoy V B, 2011 Phys. Rev. A 84 053629
Google Scholar
[17] Larson J, Anderson B M, Altland A 2013 Phys. Rev. A 87 013624
Google Scholar
[18] Rabi I I 1936 Phys. Rev. 49 324
Google Scholar
[19] Rabi I I 1937 Phys. Rev. 51 652
Google Scholar
[20] Braak D 2011 Phys. Rev. Lett. 107 100401
Google Scholar
[21] Chen Q H, Wang C, He S, Liu T, Wang K L 2012 Phys. Rev. A 86 023822
Google Scholar
[22] Solano E 2011 Physics 4 68
Google Scholar
[23] Gardas, Dajka J 2013 arXiv: 1301.5660[quant-ph]
[24] Wolf F A, Kollar M, Braak D 2012 Phys. Rev. A 85 053817
Google Scholar
[25] Walther H, Varcoe B, Englert B, Becker T 2006 Rep. Prog. Phys. 69 1325
Google Scholar
[26] Raimond J M, Brune M, Haroche S 2001 Rev. Mod. Phys. 73 565
Google Scholar
[27] Holstein T 1959 Ann. Phys. 8 325
Google Scholar
[28] Mabuchi H, Doherty A C 2002 Science 298 1372
Google Scholar
[29] Niemczyk T, Deppe F, Huebl H, Menzel E P, Hocke F, Schwarz M J, Garcia-Ripoll J J, Zueco D, Hümmer T, Solano E, Marx A, Gross R 2010 Nature Phys. 6 772
Google Scholar
[30] Forn-Diaz P, Lisenfeld J, Marcos D, Garcia-Ripoll J J, Solano E, Harmans C J P M, Mooij J E 2010 Phys. Rev. Lett. 105 237001
Google Scholar
[31] Fu Z, Wang P, Chai S, Huang L, Zhang J 2011 Phys. Rev. A 84 043609
Google Scholar
[32] Cahill K K, Glauber R J 1969 Phys. Rev. 177 1857
Google Scholar
[33] Graham R, Hohnerbach M 1984 Phys. B: Condens. Matter 57 233
Google Scholar
-
[1] 王健, 吴重庆. 低差分模式群时延少模光纤的变分法分析及优化. , 2022, 71(9): 094206. doi: 10.7498/aps.71.20212198 [2] 王志梅, 王虹, 薛乃涛, 成高艳. 自旋轨道耦合量子点系统中的量子相干. , 2022, 71(7): 078502. doi: 10.7498/aps.71.20212111 [3] 魏向杰, 孙邓, 王黎明, 严宗朝. 类锂离子体系自旋四重态费米接触项的精密计算. , 2022, 71(20): 203101. doi: 10.7498/aps.71.20220923 [4] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江. 一维 ${\cal {PT}}$ 对称非厄米自旋轨道耦合Su-Schrieffer-Heeger模型的拓扑性质. , 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796[5] 张爱霞, 姜艳芳, 薛具奎. 光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的非线性能谱特性. , 2021, 70(20): 200302. doi: 10.7498/aps.70.20210705 [6] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽. 自旋轨道耦合Su-Schrieffer-Heeger原子链系统的电子输运特性. , 2021, 70(8): 087301. doi: 10.7498/aps.70.20201742 [7] 施婷婷, 汪六九, 王璟琨, 张威. 自旋轨道耦合量子气体中的一些新进展. , 2020, 69(1): 016701. doi: 10.7498/aps.69.20191241 [8] 董成伟. 非扩散洛伦兹系统的周期轨道. , 2018, 67(24): 240501. doi: 10.7498/aps.67.20181581 [9] 李群, 陈谦, 种景. InAlN/GaN异质结二维电子气波函数的变分法研究. , 2018, 67(2): 027303. doi: 10.7498/aps.67.20171827 [10] 卢亚鑫, 马宁. 耦合电磁场对石墨烯量子磁振荡的影响. , 2016, 65(2): 027502. doi: 10.7498/aps.65.027502 [11] 陈光平. 简谐+四次势中自旋轨道耦合旋转玻色-爱因斯坦凝聚体的基态结构. , 2015, 64(3): 030302. doi: 10.7498/aps.64.030302 [12] 龚士静, 段纯刚. 金属表面Rashba自旋轨道耦合作用研究进展. , 2015, 64(18): 187103. doi: 10.7498/aps.64.187103 [13] 李桂霞, 姜永超, 凌翠翠, 马红章, 李鹏. HF+离子在旋轨耦合作用下电子态的特性. , 2014, 63(12): 127102. doi: 10.7498/aps.63.127102 [14] 熊庄, 汪振新, Naoum C. Bacalis. 基于改进变分法对原子激发态精确波函数的研究. , 2014, 63(5): 053104. doi: 10.7498/aps.63.053104 [15] 汤乃云. 耦合量子点中空穴基态反键态特性研究. , 2013, 62(5): 057301. doi: 10.7498/aps.62.057301 [16] 俞立先, 梁奇锋, 汪丽蓉, 朱士群. Rabi模型的光场压缩. , 2013, 62(16): 160301. doi: 10.7498/aps.62.160301 [17] 杨晓勇, 薛海斌, 梁九卿. 自旋相干态变换和自旋-玻色模型的基于变分法的基态解析解. , 2013, 62(11): 114205. doi: 10.7498/aps.62.114205 [18] 张磊, 李辉武, 胡梁宾. 二维自旋轨道耦合电子气中持续自旋螺旋态的稳定性的研究. , 2012, 61(17): 177203. doi: 10.7498/aps.61.177203 [19] 杨杰, 董全力, 江兆潭, 张杰. 自旋轨道耦合作用对碳纳米管电子能带结构的影响. , 2011, 60(7): 075202. doi: 10.7498/aps.60.075202 [20] 余志强, 谢泉, 肖清泉. 狭义相对论下电子自旋轨道耦合对X射线光谱的影响. , 2010, 59(2): 925-931. doi: 10.7498/aps.59.925
下载:
计量
- 文章访问数: 8418
- PDF下载量: 108
- 被引次数: 0
