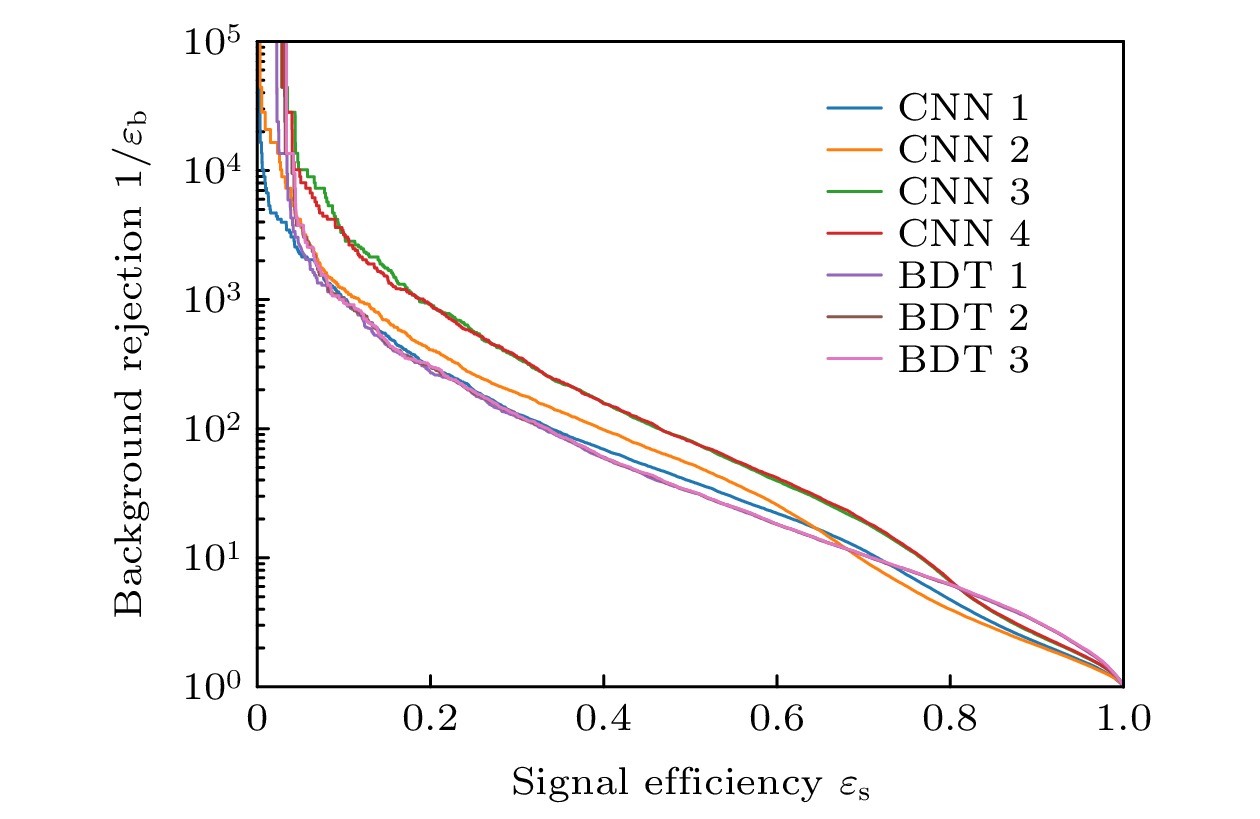
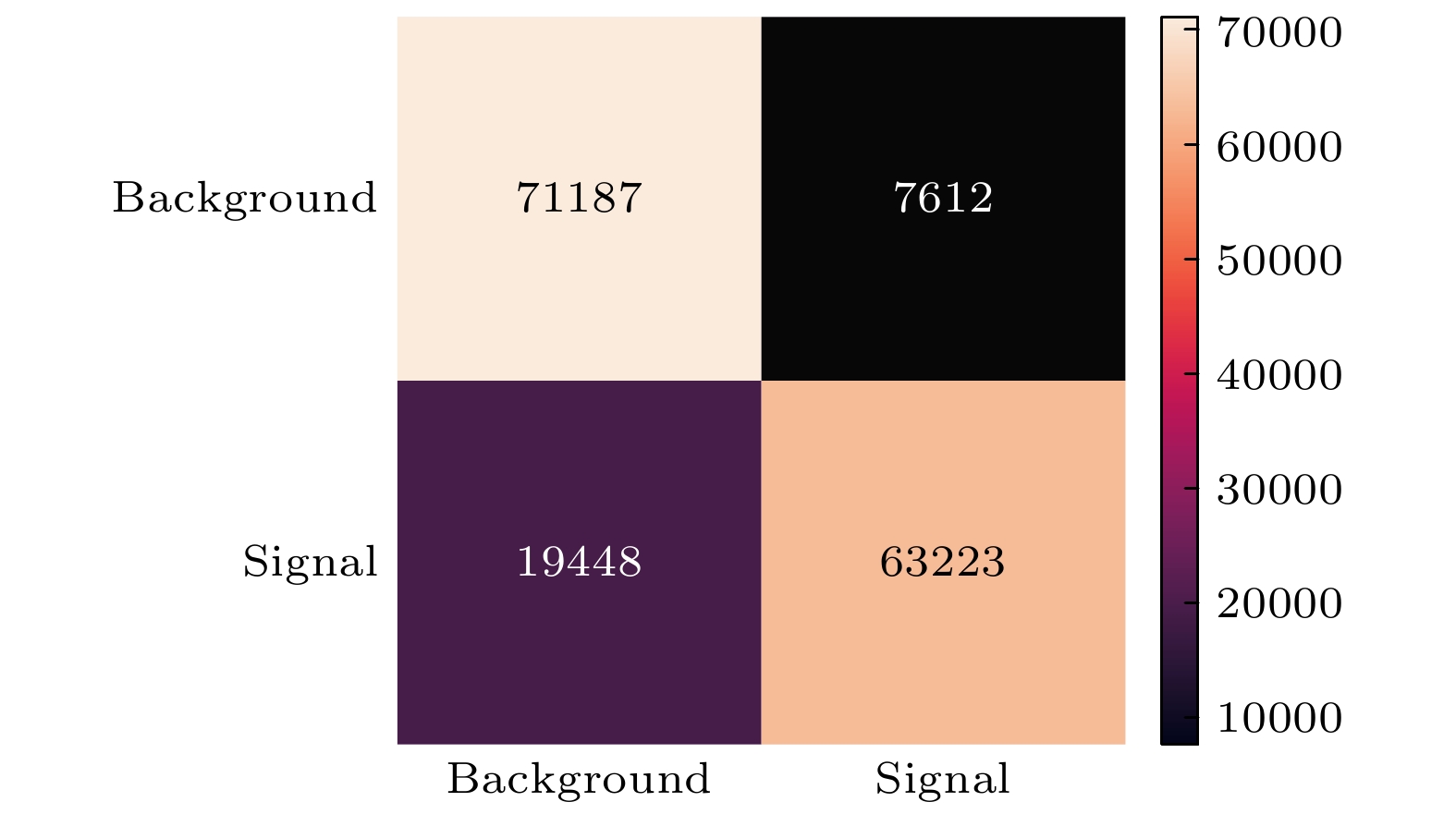
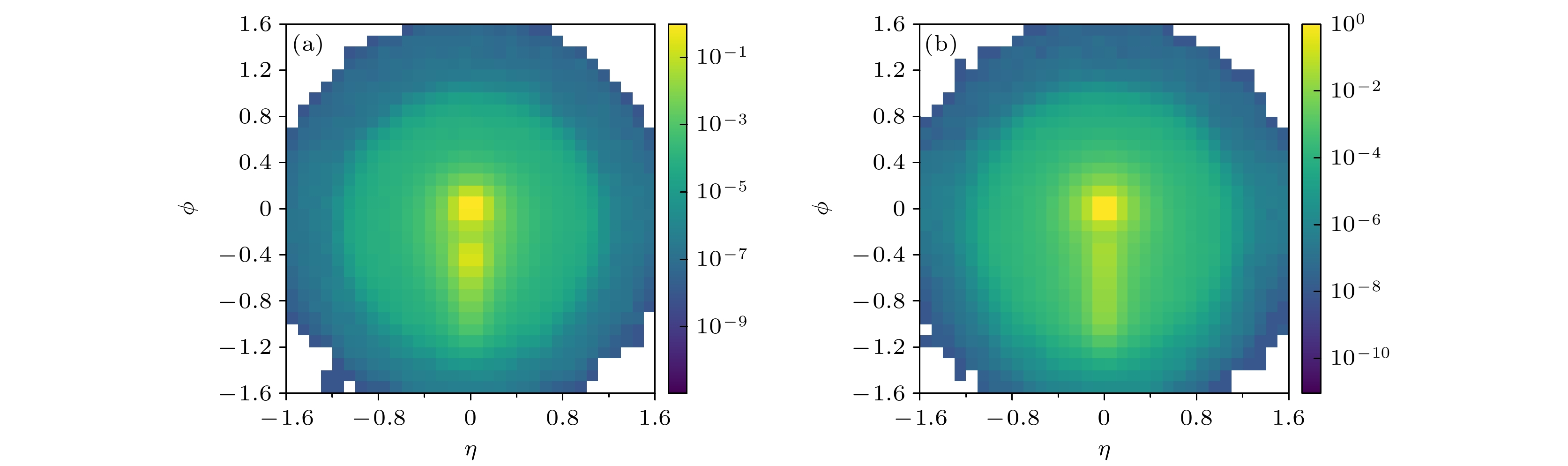
-
The jet tagging task in high-energy physics is to distinguish signals of interest from the background, which is of great importance for the discovery of new particles, or new processes, at the large hadron collider. The energy deposition generated in the calorimeter can be seen as a kind of picture. Based on this notion, tagging jets initiated by different processes becomes a classic image classification task in the computer vision field. We use jet images as the input built on high dimensional low-level information, energy-momentum four-vectors, to explore the potential of convolutional neural networks (CNNs). Four models of different depths are designed to make the best underlying useful features of jet images. Traditional multivariable method, boosted decision tree (BDT), is used as a baseline to determine the performance of networks. We introduce four observable quantities into BDTs: the mass, transverse momenta of fat jets, the distance between the leading and subleading jets, and N-subjettiness. Different tree numbers are adopted to build three kinds of BDTs, which is intended to have variable classifying abilities. After training and testing, the results show that the CNN 3 is the neatest and most efficient network under the design of stacking convolutional layers. Deepening the model could improve the performance to a certain extent but it is unable to work all the time. The performances of all BDTs are almost the same, which is possibly due to a small number of input observable types. The performance metrics show that the CNNs outperform the BDTs: the background rejection efficiency increases up to 150% at 50% signal efficiency. Besides, after inspecting the best and the worst samples, we conclude the characteristics of jets initiated by different processes: jets obtained by Z boson decays tend to concentrate in the center of jet images or have a clear differentiable substructure; the substructures of jets from general quantum chromodynamics processes have more random forms and not only just have two subjets. As the final step, the confusion matrix of the CNN 3 indicate that it comes to be kind of conservative. Exploring the way of keeping the balance between conservative and radical is our goal in the future work.
-
Keywords:
- decays of Z bosons /
- quarks /
- gluons /
- neural network
[1] Kogler R, Nachman B, Schmidt A, Asquith L, Winkels E, Campanelli M, Delitzsch C, Harris P, Hinzmann A, Kar D, McLean C, Pilot J, Takahashi Y, Tran N, Vernieri C, Vos M 2019 Rev. Mod. Phys. 91 045003
Google Scholar
[2] Kasieczka G, Plehn T, Butter A, Cranmer K, Debnath D, Dillon B M, Fairbairn M, Faroughy D A, Fedorko W, Gay C, Gouskos L, Kamenik J F, Komiske P, Leiss S, Lister A, Macaluso S, Metodiev E, Moore L, Nachman B, Nordström K, Pearkes J, Qu H, Rath Y, Rieger M, Shih D, Thompson J, Varma S 2019 SciPost Phys. 7 014
Google Scholar
[3] Larkoski A J, Moult I, Nachman B 2020 Phys. Rep. 841 1
Google Scholar
[4] 来志, 郭亮, 李小珍, 党文佳 2013 62 184207
Google Scholar
Lai Z, Guo L, Li X Z, Dang W J 2013 Acta Phys. Sin. 62 184207
Google Scholar
[5] 杨自欣, 高章然, 孙晓帆, 蔡宏灵, 张凤鸣, 吴小山 2019 68 210502
Google Scholar
Yang Z X, Gao Z R, Sun X F, Cai H L, Zhang F M, Wu X S 2019 Acta Phys. Sin. 68 210502
Google Scholar
[6] 徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元 2020 69 014209
Google Scholar
Xu Q W, Wang P P, Zeng Z J, Huang Z B, Zhou X X, Liu J M, Li Y, Chen S Q, Fan D Y 2020 Acta Phys. Sin. 69 014209
Google Scholar
[7] Cogan J, Kagan M, Strauss E, Schwarztman A 2015 J. High Energy Phys. 2015 118
Google Scholar
[8] Almeida L G, Backović M, Cliche M, Lee S J, Perelstein M 2015 J. High Energy Phys. 2015 86
Google Scholar
[9] Chen Y C J, Chiang C W, Cottin G, Shih D 2020 Phys. Rev. D 101 053001
Google Scholar
[10] Qu H, Gouskos L 2020 Phys. Rev. D 101 056019
Google Scholar
[11] Diefenbacher S, Frost H, Kasieczka G, Plehn T, Thompson J 2020 SciPost Phys. 8 023
Google Scholar
[12] Fraser K, Schwartz M D 2018 J. High Energy Phys. 2018 93
Google Scholar
[13] Macaluso S, Shih D 2018 J. High Energy Phys. 2018 121
Google Scholar
[14] Lin J, Freytsis M, Moult I, Nachman B 2018 J. High Energy Phys. 2018 101
Google Scholar
[15] Komiske P T, Metodiev E M, Schwartz M D 2017 J. High Energy Phys. 2017 110
Google Scholar
[16] Kasieczka G, Plehn T, Russell M, Schell T 2017 J. High Energy Phys. 2017 6
Google Scholar
[17] Baldi P, Bauer K, Eng C, Sadowski P, Whiteson D 2016 Phys. Rev. D 93 094034
Google Scholar
[18] Oliveira L, Kagan M, Mackey L, Nachman B, Schwartzman A 2016 J. High Energy Phys. 2016 69
Google Scholar
[19] Guest D, Collado J, Baldi P, Hsu S C, Urban G, Whiteson D 2016 Phys. Rev. D 94 112002
Google Scholar
[20] Butter A, Kasieczka G, Plehn T, Russell M 2018 SciPost Phys. 5 028
Google Scholar
[21] Kasieczka G, Kiefer N, Plehn T, Thompson J 2019 SciPost Phys. 6 069
Google Scholar
[22] Erdmann M, Geiser E, Rath Y, Rieger M 2019 J. Instrum. 14 P06006
Google Scholar
[23] Abdughani M, Ren J, Wu L, Yang J M 2019 J. High Energy Phys. 2019 55
Google Scholar
[24] Komiske P T, Metodiev E M, Thaler J 2019 J. High Energy Phys. 2019 121
Google Scholar
[25] Sjöstrand T, Ask S, Christiansen J R, Corke R, Desai N, Ilten P, Mrenna S, Prestel S, Rasmussen C O, Skands P Z 2015 Comput. Phys. Commun. 191 159
Google Scholar
[26] Cacciari M, Salam G P, Soyez G 2012 Eur. Phys. J. C 72 1896
Google Scholar
[27] Cacciari M, Salam G P, Soyez G 2008 J. High Energy Phys. 2008 63
Google Scholar
[28] Krohn D, Thaler J, Wang L T 2010 J. High Energy Phys. 2010 84
Google Scholar
-
图 1 (a)信号平均喷注图; (b)背景平均喷注图; 横坐标
$ \eta $ 代表赝快度, 纵坐标代表方位角$ \phi $ .Figure 1. (a) Signal average jet image; (b) background average jet image.
$ \eta $ and$ \phi $ represent pseudo-rapidity and azimuth respectively
图 2 CNN 3结构示意图, 产生这张图片的程序来自https://github.com/gwding/draw_convnet
Figure 2. Architecture of the CNN 3. This figure was generated by adapting the code from https://github.com/gwding/draw_convnet.
图 3 (a)胖喷注的质量分布; (b)胖喷注的横向动量分布; (c)胖喷注含有的首要与次要喷注的距离分布; (d) N-subjettiness
$ {\tau }_{21} $ 的分布Figure 3. (a) Mass distribution of fat jets; (b) transverse momentum distribution of fat jets; (c) distribution of distance between leading and subleading subjets; (d) distribution of N-subjettiness
$ {\tau }_{21} $ .
图 4 不同模型的ROC曲线
Figure 4. ROC curves of different models.
图 5 CNN 3信号神经元对于信号(橘色)与背景(蓝色)的输出分布
Figure 5. Distribution of the signal neuron of the CNN 3 on signal and background samples.
图 6 最优与最差的信号喷注图
Figure 6. The best and the worst signal jet images.
图 7 最优与最差的背景喷注图
Figure 7. The best and the worst background jet images.
图 8 CNN 3在测试集上的混淆矩阵, 其中纵坐标代表喷注图的真实类别, 横坐标代表模型预测的类别
Figure 8. Confusion matrix of the CNN 3 on the test set. The true label is on the vertical axis, and the predicted label in on the horizontal axis.
表 1 用来衡量不同模型表现的性能参数
Table 1. Metrics to evaluate performance of different models.
模型 AUC ACC R50 CNN 1 0.8754 0.8150 39.1103 CNN 2 0.8688 0.8252 53.3583 CNN 3 0.8980 0.8324 80.6715 CNN 4 0.8993 0.8328 79.9350 BDT 1 0.8955 0.8337 32.5351 BDT 2 0.8963 0.8342 32.8072 BDT 3 0.8969 0.8346 33.0144 
DownLoad: CSV
-
[1] Kogler R, Nachman B, Schmidt A, Asquith L, Winkels E, Campanelli M, Delitzsch C, Harris P, Hinzmann A, Kar D, McLean C, Pilot J, Takahashi Y, Tran N, Vernieri C, Vos M 2019 Rev. Mod. Phys. 91 045003
Google Scholar
[2] Kasieczka G, Plehn T, Butter A, Cranmer K, Debnath D, Dillon B M, Fairbairn M, Faroughy D A, Fedorko W, Gay C, Gouskos L, Kamenik J F, Komiske P, Leiss S, Lister A, Macaluso S, Metodiev E, Moore L, Nachman B, Nordström K, Pearkes J, Qu H, Rath Y, Rieger M, Shih D, Thompson J, Varma S 2019 SciPost Phys. 7 014
Google Scholar
[3] Larkoski A J, Moult I, Nachman B 2020 Phys. Rep. 841 1
Google Scholar
[4] 来志, 郭亮, 李小珍, 党文佳 2013 62 184207
Google Scholar
Lai Z, Guo L, Li X Z, Dang W J 2013 Acta Phys. Sin. 62 184207
Google Scholar
[5] 杨自欣, 高章然, 孙晓帆, 蔡宏灵, 张凤鸣, 吴小山 2019 68 210502
Google Scholar
Yang Z X, Gao Z R, Sun X F, Cai H L, Zhang F M, Wu X S 2019 Acta Phys. Sin. 68 210502
Google Scholar
[6] 徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元 2020 69 014209
Google Scholar
Xu Q W, Wang P P, Zeng Z J, Huang Z B, Zhou X X, Liu J M, Li Y, Chen S Q, Fan D Y 2020 Acta Phys. Sin. 69 014209
Google Scholar
[7] Cogan J, Kagan M, Strauss E, Schwarztman A 2015 J. High Energy Phys. 2015 118
Google Scholar
[8] Almeida L G, Backović M, Cliche M, Lee S J, Perelstein M 2015 J. High Energy Phys. 2015 86
Google Scholar
[9] Chen Y C J, Chiang C W, Cottin G, Shih D 2020 Phys. Rev. D 101 053001
Google Scholar
[10] Qu H, Gouskos L 2020 Phys. Rev. D 101 056019
Google Scholar
[11] Diefenbacher S, Frost H, Kasieczka G, Plehn T, Thompson J 2020 SciPost Phys. 8 023
Google Scholar
[12] Fraser K, Schwartz M D 2018 J. High Energy Phys. 2018 93
Google Scholar
[13] Macaluso S, Shih D 2018 J. High Energy Phys. 2018 121
Google Scholar
[14] Lin J, Freytsis M, Moult I, Nachman B 2018 J. High Energy Phys. 2018 101
Google Scholar
[15] Komiske P T, Metodiev E M, Schwartz M D 2017 J. High Energy Phys. 2017 110
Google Scholar
[16] Kasieczka G, Plehn T, Russell M, Schell T 2017 J. High Energy Phys. 2017 6
Google Scholar
[17] Baldi P, Bauer K, Eng C, Sadowski P, Whiteson D 2016 Phys. Rev. D 93 094034
Google Scholar
[18] Oliveira L, Kagan M, Mackey L, Nachman B, Schwartzman A 2016 J. High Energy Phys. 2016 69
Google Scholar
[19] Guest D, Collado J, Baldi P, Hsu S C, Urban G, Whiteson D 2016 Phys. Rev. D 94 112002
Google Scholar
[20] Butter A, Kasieczka G, Plehn T, Russell M 2018 SciPost Phys. 5 028
Google Scholar
[21] Kasieczka G, Kiefer N, Plehn T, Thompson J 2019 SciPost Phys. 6 069
Google Scholar
[22] Erdmann M, Geiser E, Rath Y, Rieger M 2019 J. Instrum. 14 P06006
Google Scholar
[23] Abdughani M, Ren J, Wu L, Yang J M 2019 J. High Energy Phys. 2019 55
Google Scholar
[24] Komiske P T, Metodiev E M, Thaler J 2019 J. High Energy Phys. 2019 121
Google Scholar
[25] Sjöstrand T, Ask S, Christiansen J R, Corke R, Desai N, Ilten P, Mrenna S, Prestel S, Rasmussen C O, Skands P Z 2015 Comput. Phys. Commun. 191 159
Google Scholar
[26] Cacciari M, Salam G P, Soyez G 2012 Eur. Phys. J. C 72 1896
Google Scholar
[27] Cacciari M, Salam G P, Soyez G 2008 J. High Energy Phys. 2008 63
Google Scholar
[28] Krohn D, Thaler J, Wang L T 2010 J. High Energy Phys. 2010 84
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5135
- PDF Downloads: 68
- Cited By: 0
