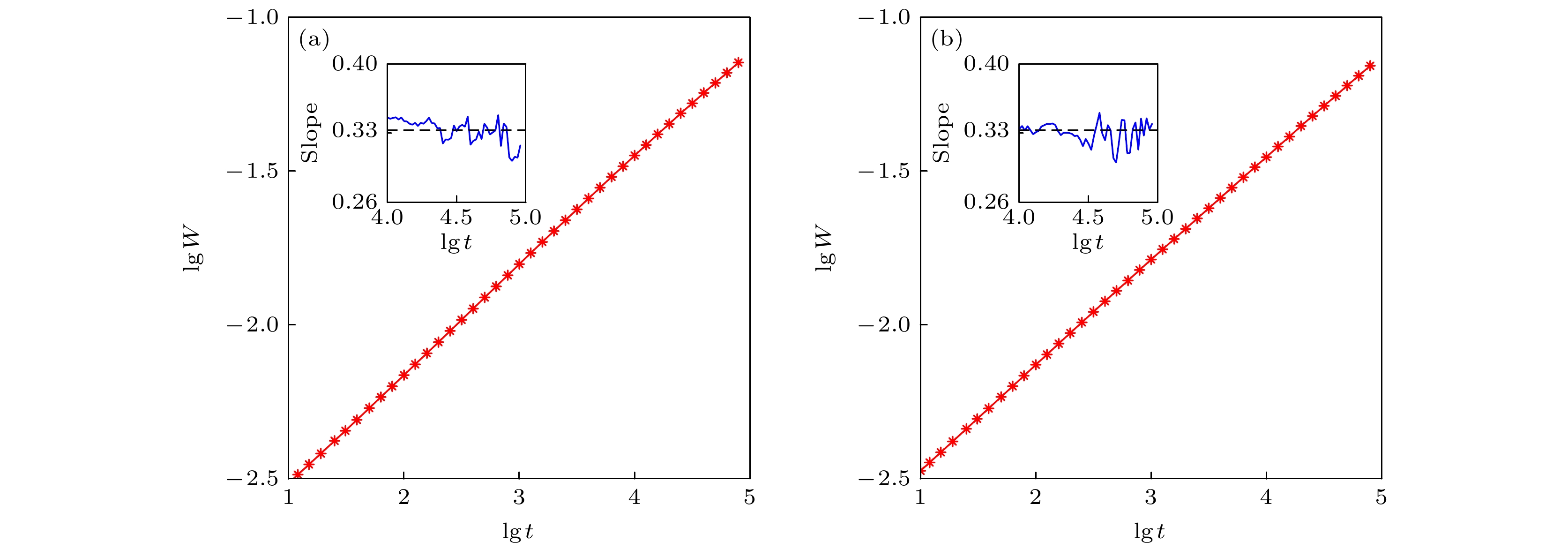
-
The Villain-Lai-Das Sarma (VLDS) equation has received much attention in surface growth dynamics due to its effective description of molecular beam epitaxy (MBE) growth process. However, the scaling exponent of the VLDS equation driven by long-range correlated noise is still unclear, because different analytical approximation methods yield inconsistent results. The nonlinear term in the VLDS equation challenges the numerical simulation methods, which often leads to the problem of numerical divergence. In the existing numerical approaches, the exponential decay techniques are mainly used to replace nonlinear terms to alleviate the numerical divergence. However, recent studies have shown that these methods may change the scaling exponent and universality class of the growth system. Therefore, we propose a novel deep neural network-based method to address this problem in this work. First, we construct a fully convolutional neural network to characterize the deterministic terms in the VLDS equation. To train the neural network, we generate training data by using the traditional finite-difference method before numerical divergence occurs. Then, we train the neural network to represent the deterministic terms, and perform simulations of VLDS driven by long-range temporally and spatially correlated noises based on the neural networks. The simulation results demonstrate that the deep neural networks constructed here possess good numerical stability. It can obtain reliable scaling exponents of the VLDS equation driven by different uncorrelated noise and correlated noise. Furthermore, in this work, it is also found that the VLDS system driven by long-range correlated noise exhibits a mound-like morphology when the temporal correlation exponent is large enough, while the growing surface morphology driven by spatially correlated noise still presents a self-affine fractal structure, independent of the spatial correlation exponent.
-
Keywords:
- neural network /
- molecular beam epitaxy growth /
- Villain-Lai-Das Sarma equation /
- dynamic scaling
[1] Cho A Y, Arthur J R 1975 Prog. Solid State Ch. 10 157
Google Scholar
[2] Panish M B 1980 Science 208 916
Google Scholar
[3] Arthur J R 2002 Surf. Sci. 500 189
Google Scholar
[4] Wolf D E, Villain J 1990 EPL 13 389
Google Scholar
[5] Das Sarma S, Tamborenea P 1991 Phys. Rev. Lett. 66 325
Google Scholar
[6] Villain J 1991 J. Phys. I 1 19
[7] Lai Z W, Das Sarma S 1991 Phys. Rev. Lett. 66 2348
Google Scholar
[8] Family F, Vicsek T S 1991 Dynamics of Fractal Surfaces (Singapore: World Scientific) pp73–132
[9] Katzav E 2002 Phys. Rev. E 65 032103
Google Scholar
[10] Tang G, Ma B 2001 Int. J. Mod. Phys. B 15 2275
Google Scholar
[11] Song T S, Xia H 2021 Phys. Rev. E 103 012121
Google Scholar
[12] Li B, Tan Z H, Jiao Y, Xia H 2021 J. Stat. Mech. Theory E 2021 023210
Google Scholar
[13] Song T S, Xia H 2021 J. Stat. Mech. Theory. E 2021 073203
Google Scholar
[14] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[15] 方波浪, 王建国, 冯国斌 2022 71 200601
Google Scholar
Fang B L, Wang J G, Feng G B 2022 Acta Phys. Sin. 71 200601
Google Scholar
[16] 田十方, 李彪 2023 72 100202
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
Google Scholar
[17] 方波浪, 武俊杰, 王晟, 吴振杰, 李天植, 张洋, 杨鹏翎, 王建国 2024 73 094301
Google Scholar
Fang B L, Wu J J, Wang S, Wu Z J, Li T Z, Zhang Y, Yang P L, Wang J G 2024 Acta Phys. Sin. 73 094301
Google Scholar
[18] Vinuesa R, Brunton S L 2022 Nat. Comput. Sci. 2 358
Google Scholar
[19] Kochkov D, Smith J A, Alieva A, Wang Q, Brenner M P, Hoyer S 2021 PNAS 118 e2101784118
Google Scholar
[20] Obiols-Sales O, Vishnu A, Malaya N, Chandramowliswharan A 2020 Proceedings of the 34th ACM International Conference on Supercomputing Barcelona Spain, June 29– July 2, 2020
[21] Ling J, Kurzawski A, Templeton J 2016 J. Fluid Mech. 807 155
Google Scholar
[22] Beck A, Flad D, Munz C D 2019 J. Comput. Phys. 398 108910
Google Scholar
[23] Rumelhart D E, Hinton G E, Williams R J 1986 Nature 323 533
Google Scholar
[24] Kingma D P, Ba J 2017 arXiv: 1412.6980 [cs. LG]
[25] Dasgupta C, Kim J M, Dutta M, Das Sarma S 1997 Phys. Rev. E 55 2235
Google Scholar
[26] Mandelbrot B B 1971 Water Resour. Res. 7 543
Google Scholar
[27] Lam C H, Sander L M 1992 Phys. Rev. A 46 R6128
Google Scholar
-
图 1 基于深度神经网络的VLDS方程数值模拟算法框图
Figure 1. Framework of deep neural network-based VLDS simulation algorithm.
图 2 VLDSNet训练阶段的损失值
Figure 2. Loss values of VLDSNet at the training stage.
图 3 VLDSNet在不同无关联噪声驱动的模拟结果 (a)均匀分布噪声; (b)高斯白噪声
Figure 3. Simulation results of VLDSNet driven by uncorrelated noise: (a) Uniformly distributed noise; (b) Gaussian white noise.
图 4 VLDSNet在长程关联噪声驱动的模拟结果 (a)长程时间关联噪声; (b)长程空间关联噪声
Figure 4. Simulation results of VLDSNet driven by long-range correlated noises: (a) Long-range temporally correlated noise; (b) long-range spatially correlated noise.
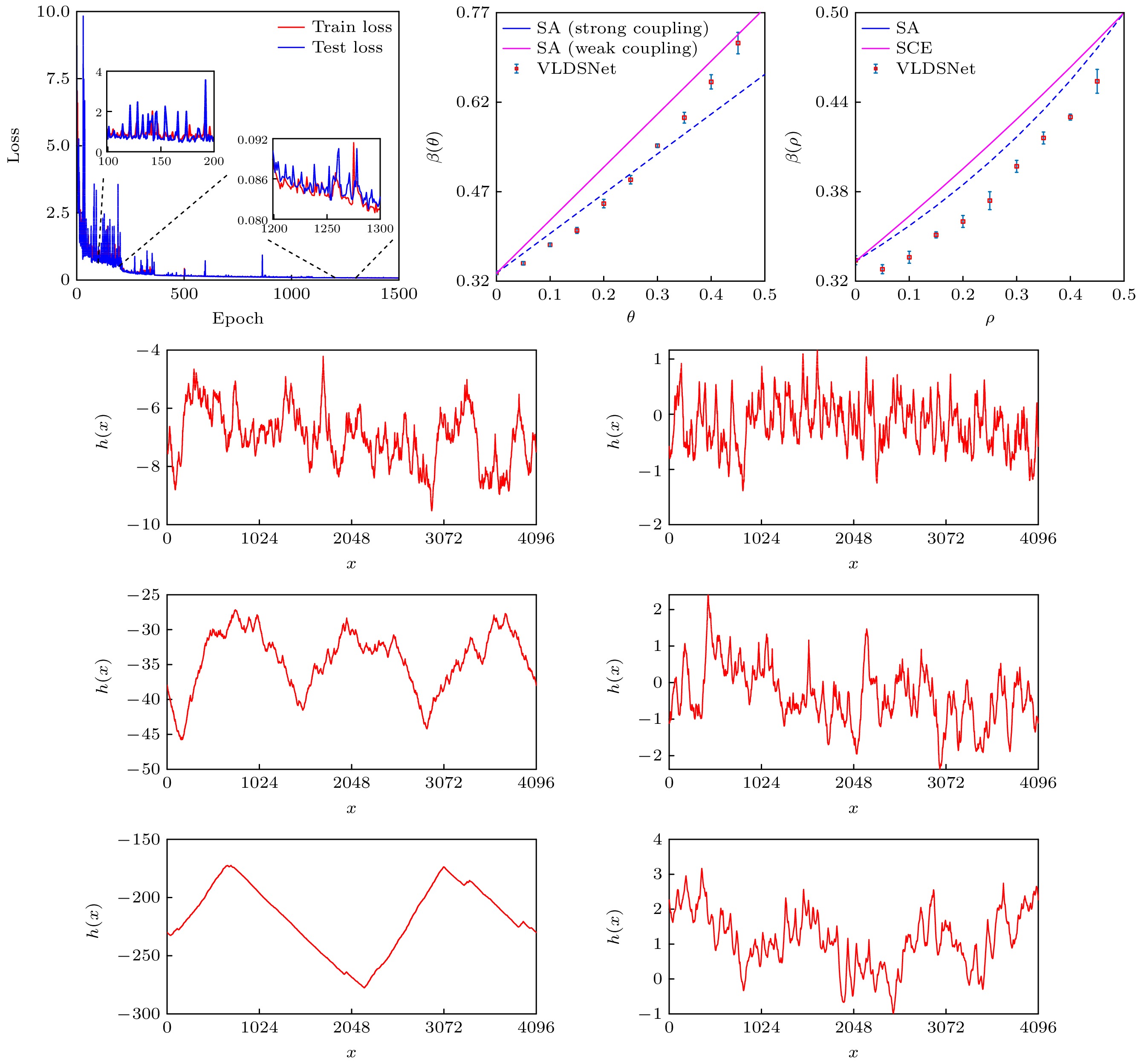
图 5 长程时间和空间关联噪声驱动的VLDS系统在稳态生长阶段的表面形貌 (a) $ \theta = 0.05 $; (b) $ \theta = 0.25 $; (c) $ \theta = 0.45 $; (d) $ \rho = $$ 0.05 $; (e) $ \rho = 0.25 $; (f) $ \rho = 0.45 $
Figure 5. Surface morphologies of VLDS system driven by long range temporally and spatially correlated noises in the steady growth regions: (a) $ \theta = 0.05 $; (b) $ \theta = 0.25 $; (c) $ \theta = 0.45 $; (d) $ \rho = 0.05 $; (e) $ \rho = 0.25 $; (f) $ \rho = 0.45 $.
表 1 VLDSNet网络结构
Table 1. Network structure of the VLDSNet.
网络层 卷积核(通道、大小、填充) 尺寸(通道×尺寸) 输入 — 1 × L 卷积层1 (9, 5, 2) 9 × L 卷积层2 (16, 3, 1) 16 × L 卷积层3 (64, 1, 0) 64 × L 卷积层4 (9, 1, 0) 9 × L 卷积层5 (1, 3, 1) 1 × L 输出 — 1 × L 
DownLoad: CSV
表 2 VLDSNet和有限差分方法数值发散比较
Table 2. Comparison of numerical divergence between VLDSNet and FD.
噪声缩放比例 离散时间步长 FD
发散时间
(高斯噪声)VLDSNet发散时间
(高斯噪声)FD
发散时间
(均匀噪声)VLDSNet发散时间
(均匀噪声)0.1 0.05 未发散 未发散 未发散 未发散 1 0.05 17.4 未发散 1728.5 未发散 10 0.05 7.0 未发散 9.9 未发散 100 0.05 5.0 未发散 6.0 未发散 0.1 0.1 2284.4 未发散 未发散 未发散 1 0.1 8.6 未发散 31.9 未发散 10 0.1 6.0 未发散 7.0 未发散 100 0.1 5.0 未发散 5.0 未发散
DownLoad: CSV
-
[1] Cho A Y, Arthur J R 1975 Prog. Solid State Ch. 10 157
Google Scholar
[2] Panish M B 1980 Science 208 916
Google Scholar
[3] Arthur J R 2002 Surf. Sci. 500 189
Google Scholar
[4] Wolf D E, Villain J 1990 EPL 13 389
Google Scholar
[5] Das Sarma S, Tamborenea P 1991 Phys. Rev. Lett. 66 325
Google Scholar
[6] Villain J 1991 J. Phys. I 1 19
[7] Lai Z W, Das Sarma S 1991 Phys. Rev. Lett. 66 2348
Google Scholar
[8] Family F, Vicsek T S 1991 Dynamics of Fractal Surfaces (Singapore: World Scientific) pp73–132
[9] Katzav E 2002 Phys. Rev. E 65 032103
Google Scholar
[10] Tang G, Ma B 2001 Int. J. Mod. Phys. B 15 2275
Google Scholar
[11] Song T S, Xia H 2021 Phys. Rev. E 103 012121
Google Scholar
[12] Li B, Tan Z H, Jiao Y, Xia H 2021 J. Stat. Mech. Theory E 2021 023210
Google Scholar
[13] Song T S, Xia H 2021 J. Stat. Mech. Theory. E 2021 073203
Google Scholar
[14] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686
Google Scholar
[15] 方波浪, 王建国, 冯国斌 2022 71 200601
Google Scholar
Fang B L, Wang J G, Feng G B 2022 Acta Phys. Sin. 71 200601
Google Scholar
[16] 田十方, 李彪 2023 72 100202
Google Scholar
Tian S F, Li B 2023 Acta Phys. Sin. 72 100202
Google Scholar
[17] 方波浪, 武俊杰, 王晟, 吴振杰, 李天植, 张洋, 杨鹏翎, 王建国 2024 73 094301
Google Scholar
Fang B L, Wu J J, Wang S, Wu Z J, Li T Z, Zhang Y, Yang P L, Wang J G 2024 Acta Phys. Sin. 73 094301
Google Scholar
[18] Vinuesa R, Brunton S L 2022 Nat. Comput. Sci. 2 358
Google Scholar
[19] Kochkov D, Smith J A, Alieva A, Wang Q, Brenner M P, Hoyer S 2021 PNAS 118 e2101784118
Google Scholar
[20] Obiols-Sales O, Vishnu A, Malaya N, Chandramowliswharan A 2020 Proceedings of the 34th ACM International Conference on Supercomputing Barcelona Spain, June 29– July 2, 2020
[21] Ling J, Kurzawski A, Templeton J 2016 J. Fluid Mech. 807 155
Google Scholar
[22] Beck A, Flad D, Munz C D 2019 J. Comput. Phys. 398 108910
Google Scholar
[23] Rumelhart D E, Hinton G E, Williams R J 1986 Nature 323 533
Google Scholar
[24] Kingma D P, Ba J 2017 arXiv: 1412.6980 [cs. LG]
[25] Dasgupta C, Kim J M, Dutta M, Das Sarma S 1997 Phys. Rev. E 55 2235
Google Scholar
[26] Mandelbrot B B 1971 Water Resour. Res. 7 543
Google Scholar
[27] Lam C H, Sander L M 1992 Phys. Rev. A 46 R6128
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 945
- PDF Downloads: 34
- Cited By: 0
