-
With the rapid development of social economy, the relationship between social members and groups has shown more complex and diverse characteristics. As a network depicting complex relation and multi-layer, hyper network has been widely used in different fields. Random network that obeys Poisson distribution is one of the pioneering models studying complex networks. In the existing hyper network researches, the hyper network based on ER random graph is still a blank. In this paper, we first propose an ER random hyper network model which is based on the hypergraph structure and it adopts the ER random graph theory. Furthermore, using this model, the node hyper degree distribution of this hyper network model is analyzed theoretically, and the node hyper degree distribution is simulated under different hyper edge probabilities:
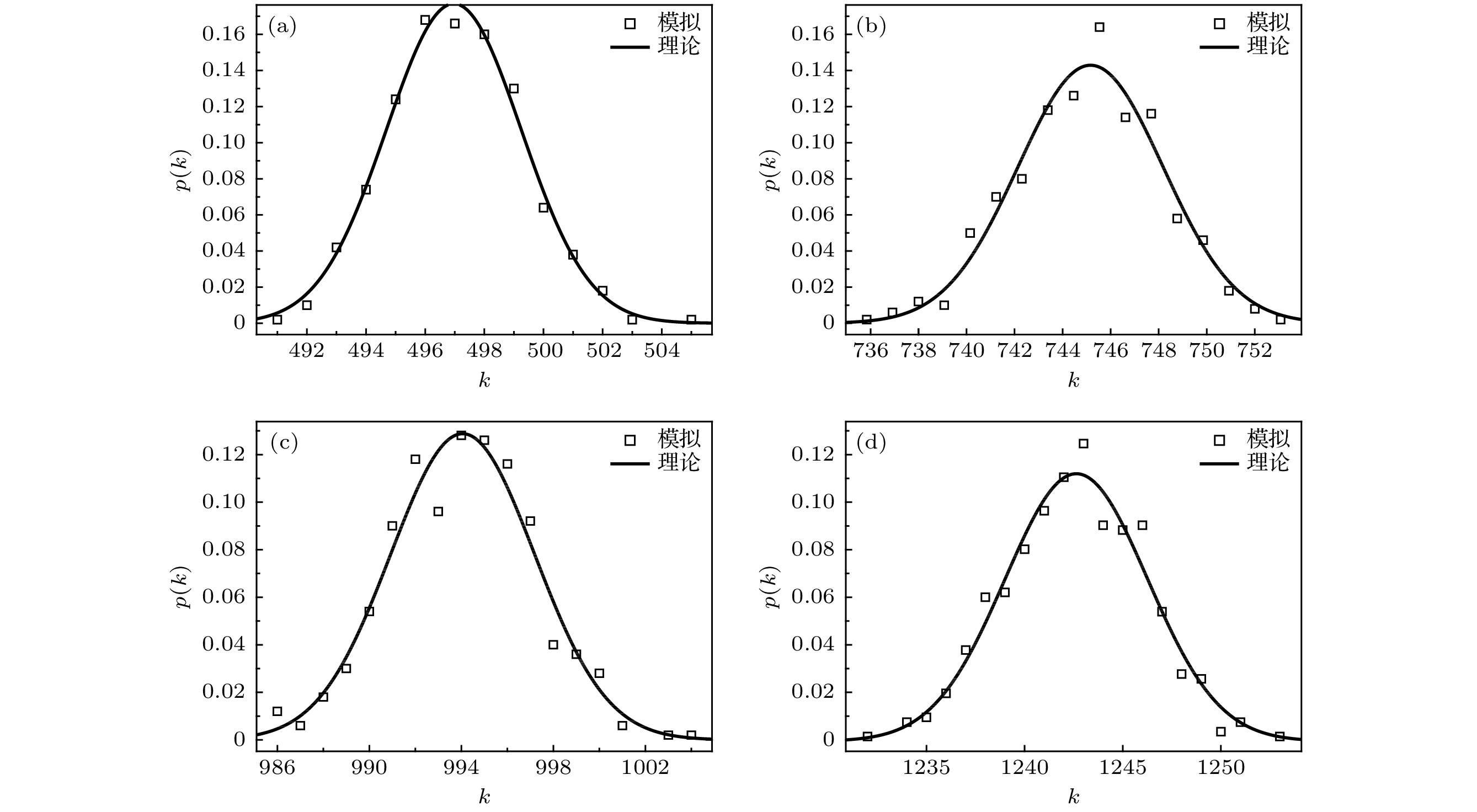
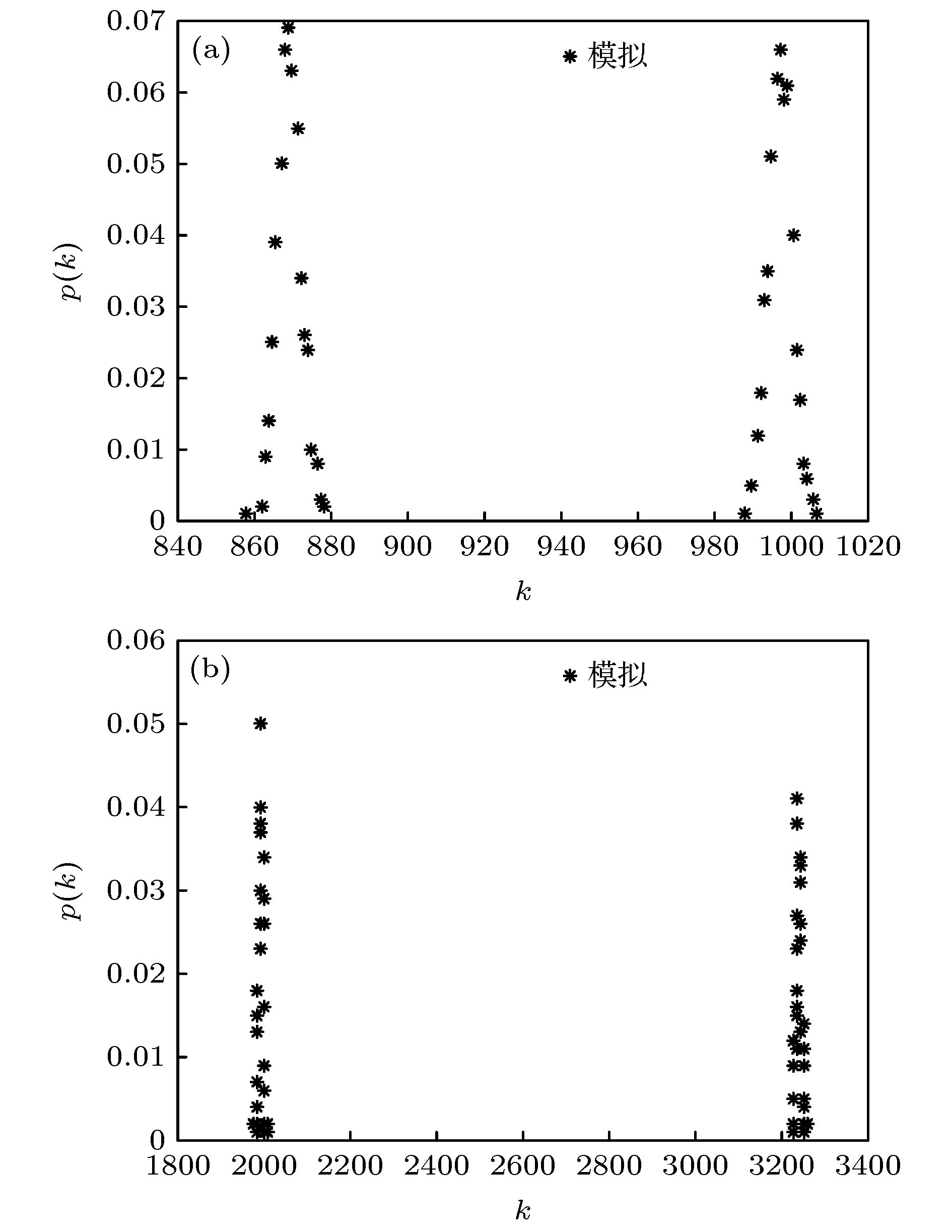
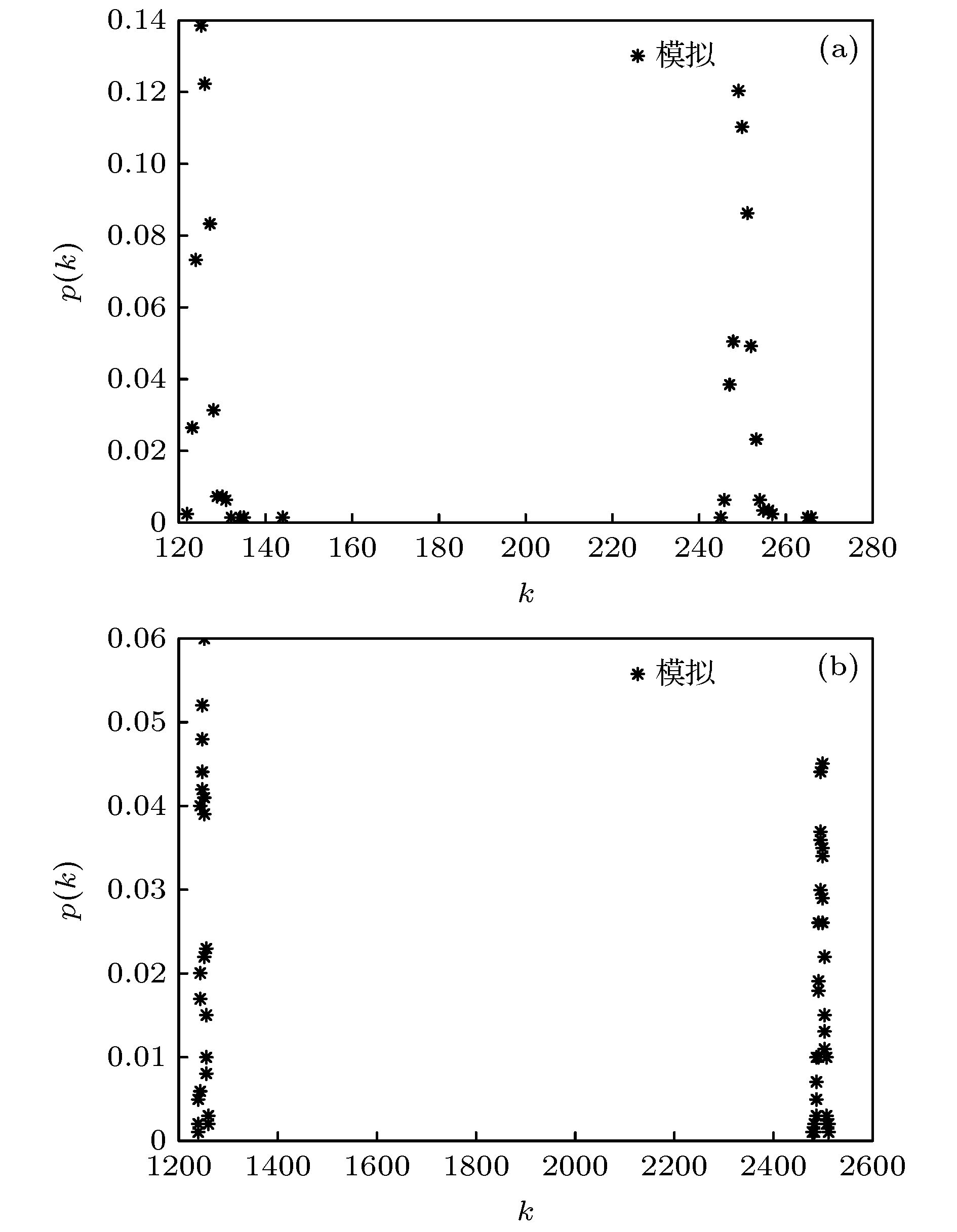
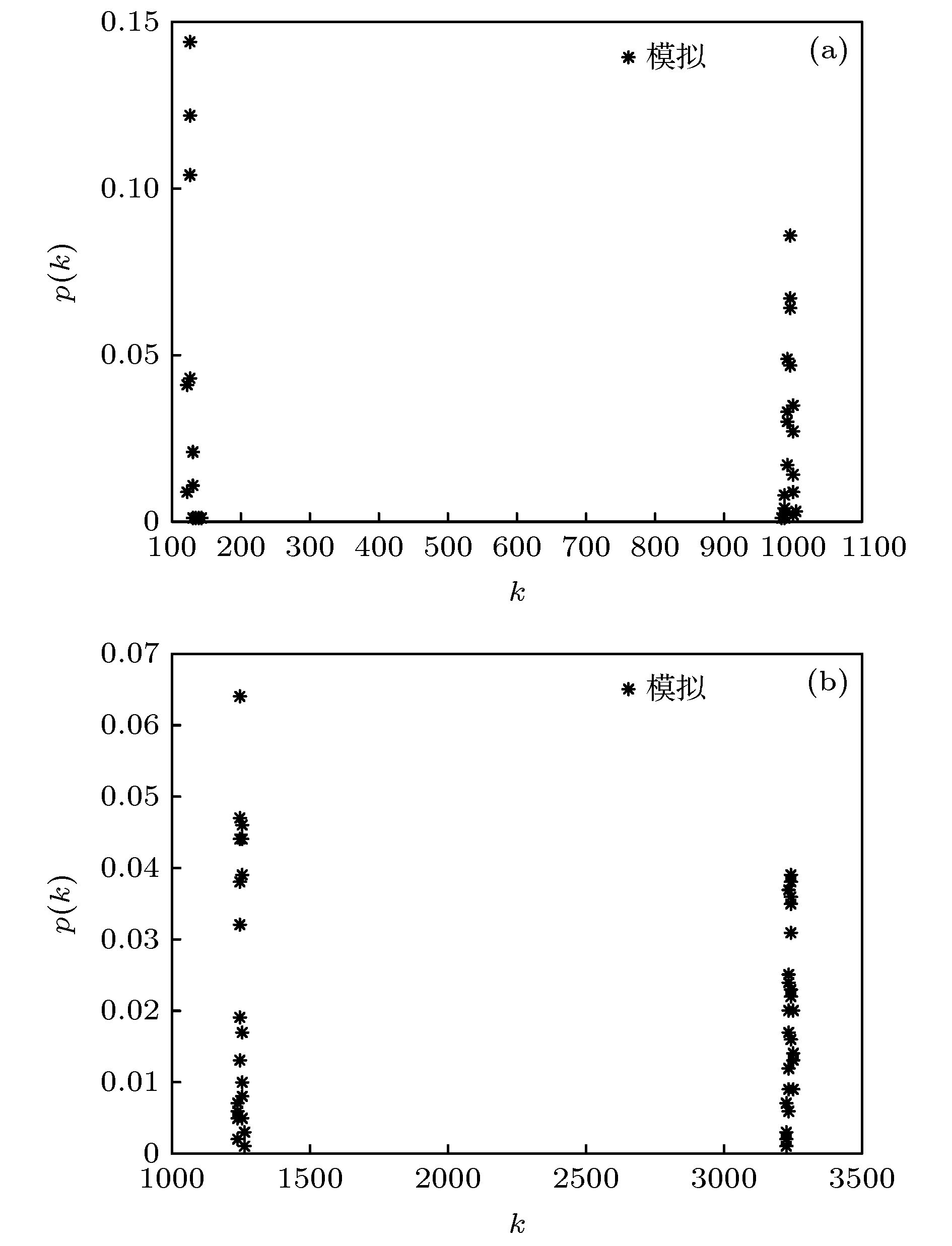
$ p=0.004$ ,$ p=0.006$ ,$ p=0.008$ and$ p=0.01$ . The results show that the node hyper degree distribution of this hyper network model complies to the Poisson distribution$p(k)\approx \dfrac{{{\left\langle \lambda \right\rangle }^{k}}}{k!}{{e}^{-\left\langle \lambda \right\rangle }}$ , which conforms with the characteristics of random networks and is consistent with the theoretical derivation. Further, in order to more accurately and effectively describe the multiple heterogeneous relationship in real life, in this paper we construct three different kinds of double-layer hyper network models with node hyper degree distribution with bimodal peak characteristics. The three kinds respectively are ER-ER, BA-BA and BA-ER, where ER represents the ER random hyper network, and BA denotes the scale-free hyper network, and the layers are connected by a random manner. The analytical expressions of node hyper degree distribution of the three kinds of double-layer hyper network models are obtained by theoretical analysis, and the average node hyper degrees of the three double-layer hyper networks are closely related to the inter-layer hyper edge probability. As the inter-layer hyper edge probability increases, the average node hyper degree increases. The results of simulation experiments show that the node hyper degree distributions of three kinds of double-layer hyper network models proposed in this paper possess the characteristics of bimodal peaks. The ER random hyper network model and the double-layer hyper network model proposed in this paper provide the theories for further studying the hyper network entropy, hyper network dynamics, hyper network representation learning, hyper network link prediction, and traffic hyper network optimization of such hyper networks in the future, and also it has certain reference significance for studying the evolution of multilayer hyper networks.-
Keywords:
- hypergraph /
- ER random hyper network /
- bimodal peaks characteristic /
- double-layer hyper network
[1] Wuchty S 2001 Mol. Biol. Evol. 18 1694
Google Scholar
[2] Wasserman S, Faust K 1994 Social Network Analysis (Cambridge: Cambridge University Press) pp1−66
[3] 汪小帆, 李翔, 陈关荣 2012 网络科学导论 (北京: 高等教育出版社) 第194 −226页
Wang X F, Li X, Chen G R 2012 Network Science: An Introduction (Beijing: Higher Education Press) pp194−226 (in Chinese)
[4] Wang P, Xu B W, Wu Y R, Zhou X Y 2015 Sci. Chin. Inf. 58 011101
[5] Lü L Y, Zhou T 2011 Phys. A 390 1150
Google Scholar
[6] Liben-Nowell D, Kleinberg J 2007 J. Am. Soc. Inf. Sci. Technol. 58 1019
Google Scholar
[7] Newman M E J 2001 Proc. Natl. Acad. Sci. 98 404
Google Scholar
[8] Zhou T, Wang B H, Jin Y D, He D R, Zhang P P, He Y, Su B B, Chen K, Zhang Z Z, Liu J G 2007 Int. J. Mod. Phys. C 18 297
Google Scholar
[9] Berge C 1973 Graphs and Hypergraphs (New York: American Elsevier Publishing Company, Inc.) pp389−425
[10] Camarinha-Matos L M, Afsarmanesh H 2003 Comput. Ind. 51 139
Google Scholar
[11] Wu Z Y, Duan J Q, Fu X C 2014 Appl. Math. Modell. 38 2961
Google Scholar
[12] 胡枫, 赵海兴, 何佳倍, 李发旭, 李淑玲, 张子柯 2013 62 198901
Google Scholar
Hu F, Zhao H X, He J B, Li F X, Li S L, Zhang Z K 2013 Acta Phys. Sin. 62 198901
Google Scholar
[13] Estrada E, Rodríguez-Velázquez J A 2006 Phys. A 364 581
Google Scholar
[14] Ghoshal G, Zlatić V, Caldarelli G, Newman M E J 2009 Phys. Rev. E 79 066118
Google Scholar
[15] Zlatić V, Ghoshal G, Caldarelli G 2009 Phys. Rev. E 80 036118
Google Scholar
[16] Zhang Z K, Liu C 2010 J. Stat. Mech. 10 1742
[17] Wang J W, Rong L L, Deng Q H 2010 Eur. Phys. J. B 77 493
Google Scholar
[18] 胡枫, 赵海兴, 马秀娟 2013 中国科学: 物理学 力学 天文学 43 16
Hu F, Zhao H X, Ma X J 2013 Sci. China, Ser. G 43 16
[19] 郭进利, 祝昕昀 2014 63 090207
Google Scholar
Guo J L, Zhu X J 2014 Acta Phys. Sin. 63 090207
Google Scholar
[20] 索琪, 郭进利 2017 系统工程理论与实践 37 720
Google Scholar
Suo Q, Guo J L 2017 System Eng. Theor. Prac. 37 720
Google Scholar
[21] Zhou Z, Jin Z, Jin J 2019 J. Phys. A 123 765
[22] 李甍娜, 郭进利, 卞闻, 常宁戈, 肖潇, 陆睿敏 2017 复杂系统与复杂性科学 4 66
Li M N, Guo J L, Bian W, Chang N G, Xiao X, Lu R M 2017 Complex Systems and Complexity Science 4 66
[23] 胡枫, 刘猛, 赵静 2018 复杂系统与复杂性科学 4 31
Hu F, Liu M, Zhao J 2018 Complex Systems and Complexity Science 4 31
[24] Fang J Q, Liu Q H, Tang M 2016 JAAC 6 12
Google Scholar
[25] 刘强, 方锦清, 李永 2015 复杂系统与复杂性科学 12 64
Liu Q, Fang J Q, Li Y 2015 Complex Systems and Complexity Science 12 64
[26] Boccaletti S, Bianconi G, Criado R 2014 Phys. Rep. 544 1
Google Scholar
[27] 蒋文君, 刘润然, 范天龙, 刘霜霜, 吕琳媛 2020 69 088904
Google Scholar
Jiang W J, Liu R R, Fan T L, Liu S S, Lü L Y 2020 Acta Phys. Sin. 69 088904
Google Scholar
[28] 杨喜艳, 吴亚豪, 张家军 2019 电子科技大学学报 10 12178
Yang X Y, Wu Y H, Zhang J J 2019 J. Elec. Sci. Tech. Univ. 10 12178
[29] Erdös P, Rényi A 1960 Publ. Math. Inst. Hung. Acad. Sci. 5 17
[30] Xu X P, Liu F 2008 Phys. Lett. A 372 6727
Google Scholar
[31] Xue X F 2017 Phys. A 486 434
Google Scholar
[32] Lima F W S, Sousa A O, Sumuor M A 2008 Phys. A 387 3503
Google Scholar
[33] Zehmakan A N 2020 Discrete. Appl. Math. 277 280
Google Scholar
[34] 李炎, 唐刚, 宋丽建, 寻之朋, 夏辉, 郝大鹏 2013 62 046401
Google Scholar
Li Y, Tang G, Song L J, Xu Z P, Xia H, Hao D P 2013 Acta Phys. Sin. 62 046401
Google Scholar
-
图 1 “航空-铁路”双层超网络模型
Figure 1. Airline-Railway double-layer hyper network.
图 2 500个节点的随机3均匀超网络在不同连接概率p值时的节点超度分布 (a)
$p = 0.004$ ; (b)$p = 0.006$ ; (c)$p = 0.008$ ; (d)$p = 0.01$ Figure 2. The hyper degree distribution of 3-uniform random hyper networks under different p: (a)
$p = 0.004$ ; (b)$p = 0.006$ ; (c)$p = 0.008$ ; (d)$p = 0.01$ .
图 3 双层3均匀EE超网络在不同层间超边连接概率时的节点超度分布 (a)
${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ Figure 3. The EE hyper degree distribution of double-layer 3-uniform hyper network under different
${p_{12}}$ : (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ .
图 4 双层3均匀BB超网络节点超度分布 (a)
${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ Figure 4. The BB hyper degree distribution of double-layer 3-uniform hyper network under different
${p_{12}}$ : (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ .
图 5 双层3均匀BE超网络模型节点超度分布 (a)
${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ Figure 5. The BE hyper degree distribution of double-layer 3-uniform hyper network under different
${p_{12}}$ : (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ .表 1 EE双层3均匀超网络实验统计
Table 1. Experimental statistics of EE hyper network.
${N_1}$ ${N_2}$ N ${p_1} = {p_2}$ ${p_{12}}$ M $\left\langle {{k_1}} \right\rangle $ $\left\langle {{k_2}} \right\rangle $ $\left\langle k \right\rangle $ 500 500 1000 0.006 0.001 62375 870 994 932 0.01 623750 1992 3240 2616 
DownLoad: CSV
表 2 BB双层3均匀超网络实验统计
Table 2. Experimental statistics of BB hyper network.
${N_1}$ ${N_2}$ N ${m_{10}} = {m_{20}}$ ${p_{12}}$ M $\left\langle {{k_1}} \right\rangle $ $\left\langle {{k_2}} \right\rangle $ $\left\langle k \right\rangle $ 500 500 1000 3 0.001 62375 126 251 188 0.01 623750 1992 3240 2616
DownLoad: CSV
表 3 BE双层3均匀超网络实验统计
Table 3. Experimental statistics of BE hyper network.
${N_1}$ ${N_2}$ N ${m_{10}}$ ${p_2}$ ${p_{12}}$ M $\left\langle {{k_1}} \right\rangle $ $\left\langle {{k_2}} \right\rangle $ $\left\langle k \right\rangle $ 500 500 1000 3 0.006 0.001 62375 126 994 560 0.01 623750 1249 3240 2244
DownLoad: CSV
-
[1] Wuchty S 2001 Mol. Biol. Evol. 18 1694
Google Scholar
[2] Wasserman S, Faust K 1994 Social Network Analysis (Cambridge: Cambridge University Press) pp1−66
[3] 汪小帆, 李翔, 陈关荣 2012 网络科学导论 (北京: 高等教育出版社) 第194 −226页
Wang X F, Li X, Chen G R 2012 Network Science: An Introduction (Beijing: Higher Education Press) pp194−226 (in Chinese)
[4] Wang P, Xu B W, Wu Y R, Zhou X Y 2015 Sci. Chin. Inf. 58 011101
[5] Lü L Y, Zhou T 2011 Phys. A 390 1150
Google Scholar
[6] Liben-Nowell D, Kleinberg J 2007 J. Am. Soc. Inf. Sci. Technol. 58 1019
Google Scholar
[7] Newman M E J 2001 Proc. Natl. Acad. Sci. 98 404
Google Scholar
[8] Zhou T, Wang B H, Jin Y D, He D R, Zhang P P, He Y, Su B B, Chen K, Zhang Z Z, Liu J G 2007 Int. J. Mod. Phys. C 18 297
Google Scholar
[9] Berge C 1973 Graphs and Hypergraphs (New York: American Elsevier Publishing Company, Inc.) pp389−425
[10] Camarinha-Matos L M, Afsarmanesh H 2003 Comput. Ind. 51 139
Google Scholar
[11] Wu Z Y, Duan J Q, Fu X C 2014 Appl. Math. Modell. 38 2961
Google Scholar
[12] 胡枫, 赵海兴, 何佳倍, 李发旭, 李淑玲, 张子柯 2013 62 198901
Google Scholar
Hu F, Zhao H X, He J B, Li F X, Li S L, Zhang Z K 2013 Acta Phys. Sin. 62 198901
Google Scholar
[13] Estrada E, Rodríguez-Velázquez J A 2006 Phys. A 364 581
Google Scholar
[14] Ghoshal G, Zlatić V, Caldarelli G, Newman M E J 2009 Phys. Rev. E 79 066118
Google Scholar
[15] Zlatić V, Ghoshal G, Caldarelli G 2009 Phys. Rev. E 80 036118
Google Scholar
[16] Zhang Z K, Liu C 2010 J. Stat. Mech. 10 1742
[17] Wang J W, Rong L L, Deng Q H 2010 Eur. Phys. J. B 77 493
Google Scholar
[18] 胡枫, 赵海兴, 马秀娟 2013 中国科学: 物理学 力学 天文学 43 16
Hu F, Zhao H X, Ma X J 2013 Sci. China, Ser. G 43 16
[19] 郭进利, 祝昕昀 2014 63 090207
Google Scholar
Guo J L, Zhu X J 2014 Acta Phys. Sin. 63 090207
Google Scholar
[20] 索琪, 郭进利 2017 系统工程理论与实践 37 720
Google Scholar
Suo Q, Guo J L 2017 System Eng. Theor. Prac. 37 720
Google Scholar
[21] Zhou Z, Jin Z, Jin J 2019 J. Phys. A 123 765
[22] 李甍娜, 郭进利, 卞闻, 常宁戈, 肖潇, 陆睿敏 2017 复杂系统与复杂性科学 4 66
Li M N, Guo J L, Bian W, Chang N G, Xiao X, Lu R M 2017 Complex Systems and Complexity Science 4 66
[23] 胡枫, 刘猛, 赵静 2018 复杂系统与复杂性科学 4 31
Hu F, Liu M, Zhao J 2018 Complex Systems and Complexity Science 4 31
[24] Fang J Q, Liu Q H, Tang M 2016 JAAC 6 12
Google Scholar
[25] 刘强, 方锦清, 李永 2015 复杂系统与复杂性科学 12 64
Liu Q, Fang J Q, Li Y 2015 Complex Systems and Complexity Science 12 64
[26] Boccaletti S, Bianconi G, Criado R 2014 Phys. Rep. 544 1
Google Scholar
[27] 蒋文君, 刘润然, 范天龙, 刘霜霜, 吕琳媛 2020 69 088904
Google Scholar
Jiang W J, Liu R R, Fan T L, Liu S S, Lü L Y 2020 Acta Phys. Sin. 69 088904
Google Scholar
[28] 杨喜艳, 吴亚豪, 张家军 2019 电子科技大学学报 10 12178
Yang X Y, Wu Y H, Zhang J J 2019 J. Elec. Sci. Tech. Univ. 10 12178
[29] Erdös P, Rényi A 1960 Publ. Math. Inst. Hung. Acad. Sci. 5 17
[30] Xu X P, Liu F 2008 Phys. Lett. A 372 6727
Google Scholar
[31] Xue X F 2017 Phys. A 486 434
Google Scholar
[32] Lima F W S, Sousa A O, Sumuor M A 2008 Phys. A 387 3503
Google Scholar
[33] Zehmakan A N 2020 Discrete. Appl. Math. 277 280
Google Scholar
[34] 李炎, 唐刚, 宋丽建, 寻之朋, 夏辉, 郝大鹏 2013 62 046401
Google Scholar
Li Y, Tang G, Song L J, Xu Z P, Xia H, Hao D P 2013 Acta Phys. Sin. 62 046401
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7166
- PDF Downloads: 119
- Cited By: 0
