-
The spatial structure and social diversity playing a nontrivial role in the emergence and maintenance of cooperation among selfish individuals have been verified. Their effects on the evolution of cooperation have attracted great attention in recent years. Most of previous evolutionary game dynamics is based on pairwise interactions. However, the interactions often take place within groups of people in many real situations and cannot be described simply by dyads. The dynamics of evolutionary games in systems with higher-order interactions has not yet been explored as deserved. In this paper, we introduce heterogeneous multiplication factors into the spatial public goods game to investigate the cooperative behaviors on the hypergraphs. In addition to the original model in which all groups have the same multiplication factor, three types of heterogeneous multiplication factor distributions including uniform, exponential and power-law distributions are considered. The numerical simulation results show that the increase of the order g of the uniform random hypergraphs is conducive to the emergence and prosperity of the individuals' cooperative behavior no matter what types these distributions belong to. Furthermore, compared with the results of the original spatial public goods games on hypergraphs, the heterogeneous multiplication factors following three different distributions can remarkably promote the evolution of cooperation. In particular, for most of ranges of the average rescaling multiplication factor
$r_0$ , the highest cooperation level can be obtained under the power-law distribution, while the uniform distribution leads to the lowest cooperation level. We provide an explanation through investigating the number of cooperators in each group. In addition, to probe into the essence that influences the survival of cooperative behaviors, we study the time series of the fraction of groups with different numbers of cooperators. Besides, we also investigate the influence of the number of hyperlinks on cooperation evolution. We find that the results are robust against the number of hyperlinks L, and the emergence of cooperative behaviors in public goods games on hypergraphs is hindered with the value of L increasing. To some extent, these results are helpful in the better understanding of the evolutionary dynamics of the spatial public goods games on hypergraphs with social diversity.[1] Axelrod R, Hamilton W 1981 Science 211 1390
Google Scholar
[2] Szabó G, Fáth G 2007 Phys. Rep. 446 97
Google Scholar
[3] Nowak M A, May R M 1992 Nature 359 826
Google Scholar
[4] Szabó G, Borsos I 2016 Phys. Rep. 624 1
Google Scholar
[5] Perc M, Jordan J J, Rand D G, Wang Z, Boccaletti S, Szolnoki A 2017 Phys. Rep. 687 1
Google Scholar
[6] Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, Young J G, Petri G 2020 Phys. Rep. 874 1
Google Scholar
[7] Santos F C, Santos M D, Pacheco J M 2008 Nature 454 213
Google Scholar
[8] Rong Z, Wu Z X 2009 Europhys. Lett. 87 30001
Google Scholar
[9] Battiston F, Perc M, Latora V 2017 New J. Phys. 19 073017
Google Scholar
[10] Huang C W, Han W C, Li H H, Cheng H Y, Dai Q L, Yang J Z 2019 Appl. Math. Comput. 340 305
Google Scholar
[11] Szolnoki A, Perc M 2010 Europhys. Lett. 92 38003
Google Scholar
[12] Brandt H, Hauert C, Sigmund K 2003 Proc. R. Soc. London, Ser. B 270 1099
Google Scholar
[13] Helbing D, Szolnoki A, Perc M, Szabó G 2010 New J. Phys. 12 083005
Google Scholar
[14] Chen X, Szolnoki A, Perc M 2014 New J. Phys. 16 083016
Google Scholar
[15] Yang H X, Rong Z H 2015 Chaos Solitons Fractals 77 230
Google Scholar
[16] Yang H X, Chen X 2018 Appl. Math. Comput. 316 460
Google Scholar
[17] Zhang Y C, Wang J, Ding C X, Xia C 2017 Knowledge-Based Systems 136 150
Google Scholar
[18] Zhang L, Xie Y, Huang C W, Li H H, Dai Q L 2020 Chaos, Solitons Fractals 133 109675
Google Scholar
[19] Liu L, Chen X, Perc M 2019 Nonlinear Dynamics 97 749
Google Scholar
[20] Liu L, Chen X 2020 Knowledge-Based Systems 188 104835
Google Scholar
[21] Chen M, Wang L, Wang J, Sun S, Xia C 2015 Appl. Math. Comput. 251 192
Google Scholar
[22] Szolnoki A, Chen X 2015 Phys. Rev. E 92 042813
Google Scholar
[23] Szolnoki A, Perc M 2016 New J. Phys. 18 083021
Google Scholar
[24] Javarone M A, Antonioni A, Caravelli F 2016 Europhys. Lett. 114 38001
Google Scholar
[25] Pei Z, Wang B, Du J 2017 New J. Phys. 19 013037
Google Scholar
[26] Shi D M, Zhuang Y, Wang B H 2010 Europhys. Lett. 90 58003
Google Scholar
[27] Shi D M, Zhuang Y, Wang B H 2012 Physica A 391 1636
Google Scholar
[28] Chen X, Liu Y, Zhou Y, Wang L, Perc M 2012 PLoS One 7 e36895
Google Scholar
[29] Weng Q, He N, Hu L, Chen X 2021 Phys. Lett. A 400 127299
Google Scholar
[30] 郭进利, 祝昕昀 2014 63 090207
Google Scholar
Guo J L, Zhu X Y 2014 Acta Phys. Sin. 63 090207
Google Scholar
[31] 卢文, 赵海兴, 孟磊, 胡枫 2021 70 018901
Google Scholar
Lu W, Zhao H X, Meng L, Hu F 2021 Acta Phys. Sin. 70 018901
Google Scholar
[32] Vasilyeva E, Kozlov A, Alfaro-Bittner K, Musatov D, Raigorodskii A M, Perc M, Boccaletti S 2021 Sci. Rep. 11 5666
Google Scholar
[33] Battiston F, Amico E, Barrat A, Bianconi G, Ferraz de Arruda G, Franceschiello B, Iacopini I, Kéfi S, Latora V, Moreno Y, Murray M M, Peixoto T P, Vaccarino F, Petri G 2021 Nat. Phys. 17 1093
Google Scholar
[34] Burgio G, Matamalas J T, Gómez S, Arenas A 2020 Entropy 22 744
Google Scholar
[35] Alvarez-Rodriguez U, Battiston F, de Arruda G F, Moreno Y, Perc M, Latora V 2021 Nature Human Behaviour 5 586
Google Scholar
[36] Perc M, Szolnoki A 2008 Phys. Rev. E 77 011904
Google Scholar
[37] Taylor P, Jonker L 1978 Math. Biosci. 40 145
Google Scholar
-
图 1 3阶均匀随机超图上的空间公共品博弈
Figure 1. The spatial public goods game on uniform random hypergraph with hyperlinks of order equal to g = 3.
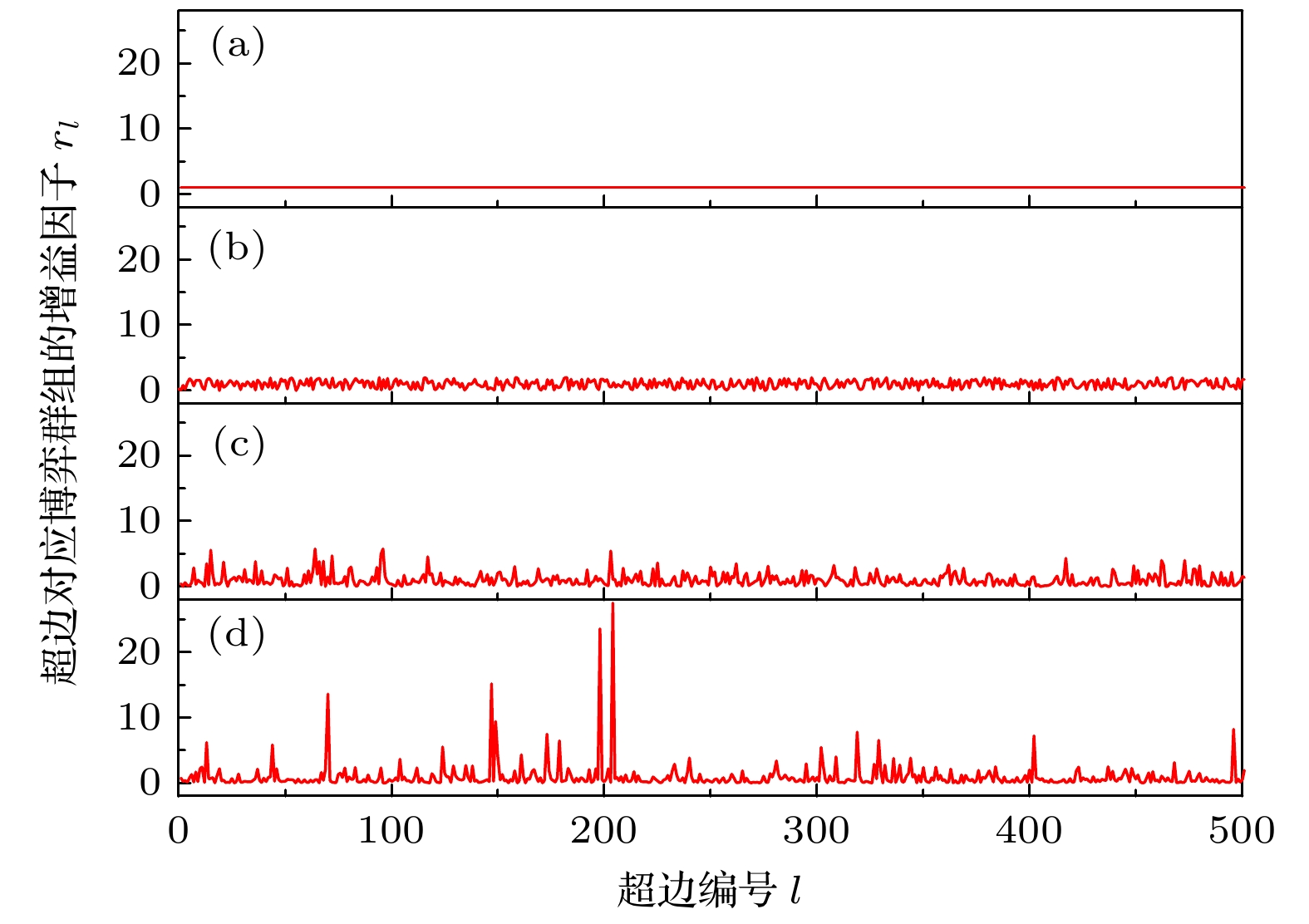
图 2
$ r_0 = 1.0 $ 和$ a = 1.0 $ 时4种分布情况下的群体增益因子$ r_{l} = r_0(1 + \xi) $ 的分布 (a) 原始模型; (b) 均匀分布; (c) 指数分布; (d) 幂律分布Figure 2. Distributions of synergy factors
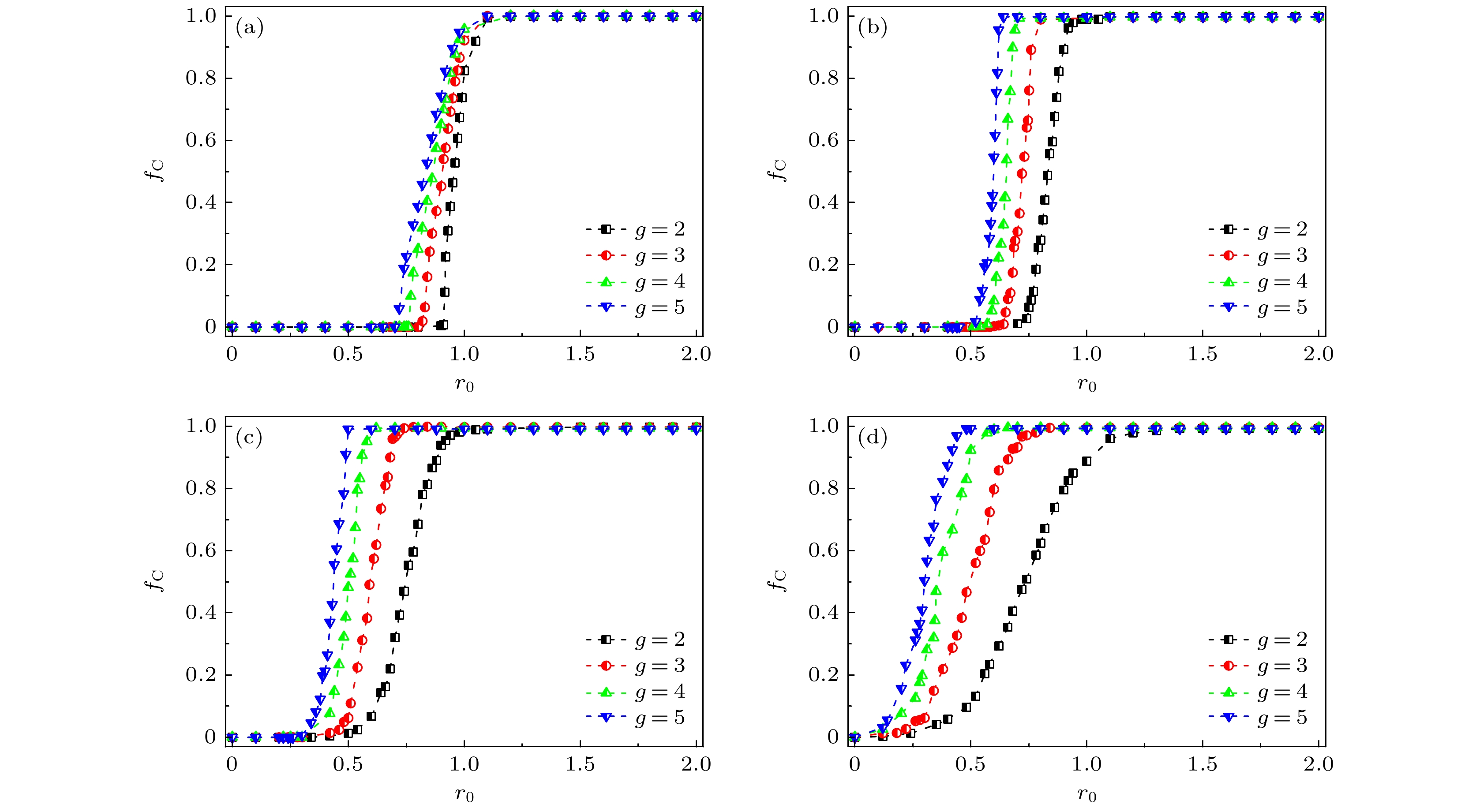
$ r_{l} = r_0(1 + \xi) $ for$ r_0 = 1.0 $ and$ a = 1.0 $ of the four cases: (a) Original model; (b) uniform distribution; (c) exponential distribution; (d) power-law distribution.
图 3 4种增益因子分布情况下, 不同阶数
$ g $ 的超图上群体合作水平$f_{\rm{C}}$ 随$ r_0 $ 的变化 (a) 原始模型; (b) 均匀分布; (c) 指数分布; (d) 幂律分布Figure 3. Fraction of cooperators
$ f_{\rm{C}} $ as a function of$ r_0 $ for hypergraphs with different orders$ g $ : (a) Original model; (b) uniform distribution; (c) exponential distribution; (d) power-law distribution
图 4 不同超图阶数
$ g $ 值情况下, 4种增益因子分布对应的群体合作水平$f_{\rm{C}}$ 随$ r_0 $ 的变化 (a)$ g = 2 $ ; (b)$ g = 3 $ ; (c)$ g = 4 $ ; (d)$ g = 5 $ Figure 4. Fraction of cooperators
$ f_{\rm{C}} $ as a function of$ r_0 $ on hypergraphs with (a)$ g = 2 $ , (b)$ g = 3 $ , (c)$ g = 4 $ and (d)$ g = 5 $ for the four situations
图 5 参数取
$ g = 5 $ 与$ r_0 = 0.35 $ 时博弈群组单元中合作者数目$w_{\rm{C }}$ 的分布Figure 5. Distribution of the numbers of cooperators in the group
$w_{\rm{C}}$ for$ g = 5 $ and$ r_0 = 0.35 $ 
图 6 4种增益因子分布情况下, 参数取
$ g = 5 $ 与$ r_0 = 0.35 $ 时群体合作水平$ f_{\rm{C}} $ 以及群组中合作者数目$ w_{\rm{C}} $ 分别为0, 1, 2, 3, 4, 5的博弈群组比例的演化时间序列 (a) 原始模型; (b) 均匀分布; (c) 指数分布; (d) 幂律分布Figure 6. Time series for the evolution of the fraction of cooperators
$ f_{\rm{C}} $ and the fractions of groups with$ w_{\rm{C}} = 0, 1, 2, 3, 4, 5 $ for$ g = 5 $ and$ r_0 = 0.35 $ : (a) Original model; (b) uniform distribution; (c) exponential distribution; (d) power-law distribution
图 7 4种增益因子分布情况下, 不同阶数
$ g $ 的超图上临界增益因子均值$r_{\rm{c}}$ 随超边数目$ L $ 与阈值$ L_{\rm{c}} $ 的比值的变化 (a) 原始模型; (b) 均匀分布; (c) 指数分布; (d) 幂律分布Figure 7. Critical value of the synergy factor
$ r_{\rm{c}} $ as a function of the ratio between the number of hyperlinks$ L $ and the critical value$ L_{\rm{c}} $ in hypergraphs of different orders$ g $ : (a) Original model; (b) uniform distribution; (c) exponential distribution; (d) power-law distribution -
[1] Axelrod R, Hamilton W 1981 Science 211 1390
Google Scholar
[2] Szabó G, Fáth G 2007 Phys. Rep. 446 97
Google Scholar
[3] Nowak M A, May R M 1992 Nature 359 826
Google Scholar
[4] Szabó G, Borsos I 2016 Phys. Rep. 624 1
Google Scholar
[5] Perc M, Jordan J J, Rand D G, Wang Z, Boccaletti S, Szolnoki A 2017 Phys. Rep. 687 1
Google Scholar
[6] Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, Young J G, Petri G 2020 Phys. Rep. 874 1
Google Scholar
[7] Santos F C, Santos M D, Pacheco J M 2008 Nature 454 213
Google Scholar
[8] Rong Z, Wu Z X 2009 Europhys. Lett. 87 30001
Google Scholar
[9] Battiston F, Perc M, Latora V 2017 New J. Phys. 19 073017
Google Scholar
[10] Huang C W, Han W C, Li H H, Cheng H Y, Dai Q L, Yang J Z 2019 Appl. Math. Comput. 340 305
Google Scholar
[11] Szolnoki A, Perc M 2010 Europhys. Lett. 92 38003
Google Scholar
[12] Brandt H, Hauert C, Sigmund K 2003 Proc. R. Soc. London, Ser. B 270 1099
Google Scholar
[13] Helbing D, Szolnoki A, Perc M, Szabó G 2010 New J. Phys. 12 083005
Google Scholar
[14] Chen X, Szolnoki A, Perc M 2014 New J. Phys. 16 083016
Google Scholar
[15] Yang H X, Rong Z H 2015 Chaos Solitons Fractals 77 230
Google Scholar
[16] Yang H X, Chen X 2018 Appl. Math. Comput. 316 460
Google Scholar
[17] Zhang Y C, Wang J, Ding C X, Xia C 2017 Knowledge-Based Systems 136 150
Google Scholar
[18] Zhang L, Xie Y, Huang C W, Li H H, Dai Q L 2020 Chaos, Solitons Fractals 133 109675
Google Scholar
[19] Liu L, Chen X, Perc M 2019 Nonlinear Dynamics 97 749
Google Scholar
[20] Liu L, Chen X 2020 Knowledge-Based Systems 188 104835
Google Scholar
[21] Chen M, Wang L, Wang J, Sun S, Xia C 2015 Appl. Math. Comput. 251 192
Google Scholar
[22] Szolnoki A, Chen X 2015 Phys. Rev. E 92 042813
Google Scholar
[23] Szolnoki A, Perc M 2016 New J. Phys. 18 083021
Google Scholar
[24] Javarone M A, Antonioni A, Caravelli F 2016 Europhys. Lett. 114 38001
Google Scholar
[25] Pei Z, Wang B, Du J 2017 New J. Phys. 19 013037
Google Scholar
[26] Shi D M, Zhuang Y, Wang B H 2010 Europhys. Lett. 90 58003
Google Scholar
[27] Shi D M, Zhuang Y, Wang B H 2012 Physica A 391 1636
Google Scholar
[28] Chen X, Liu Y, Zhou Y, Wang L, Perc M 2012 PLoS One 7 e36895
Google Scholar
[29] Weng Q, He N, Hu L, Chen X 2021 Phys. Lett. A 400 127299
Google Scholar
[30] 郭进利, 祝昕昀 2014 63 090207
Google Scholar
Guo J L, Zhu X Y 2014 Acta Phys. Sin. 63 090207
Google Scholar
[31] 卢文, 赵海兴, 孟磊, 胡枫 2021 70 018901
Google Scholar
Lu W, Zhao H X, Meng L, Hu F 2021 Acta Phys. Sin. 70 018901
Google Scholar
[32] Vasilyeva E, Kozlov A, Alfaro-Bittner K, Musatov D, Raigorodskii A M, Perc M, Boccaletti S 2021 Sci. Rep. 11 5666
Google Scholar
[33] Battiston F, Amico E, Barrat A, Bianconi G, Ferraz de Arruda G, Franceschiello B, Iacopini I, Kéfi S, Latora V, Moreno Y, Murray M M, Peixoto T P, Vaccarino F, Petri G 2021 Nat. Phys. 17 1093
Google Scholar
[34] Burgio G, Matamalas J T, Gómez S, Arenas A 2020 Entropy 22 744
Google Scholar
[35] Alvarez-Rodriguez U, Battiston F, de Arruda G F, Moreno Y, Perc M, Latora V 2021 Nature Human Behaviour 5 586
Google Scholar
[36] Perc M, Szolnoki A 2008 Phys. Rev. E 77 011904
Google Scholar
[37] Taylor P, Jonker L 1978 Math. Biosci. 40 145
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4883
- PDF Downloads: 123
- Cited By: 0
