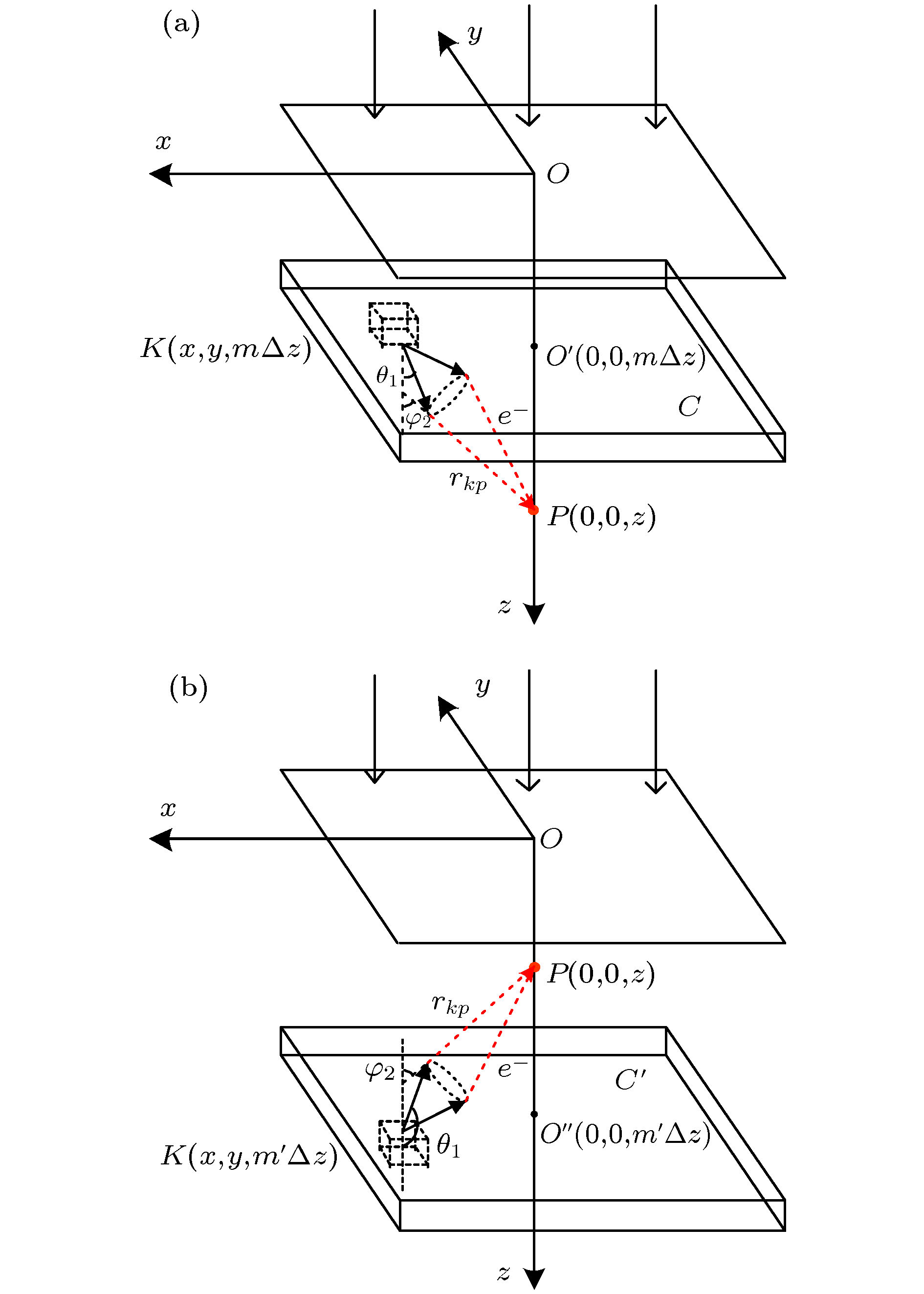
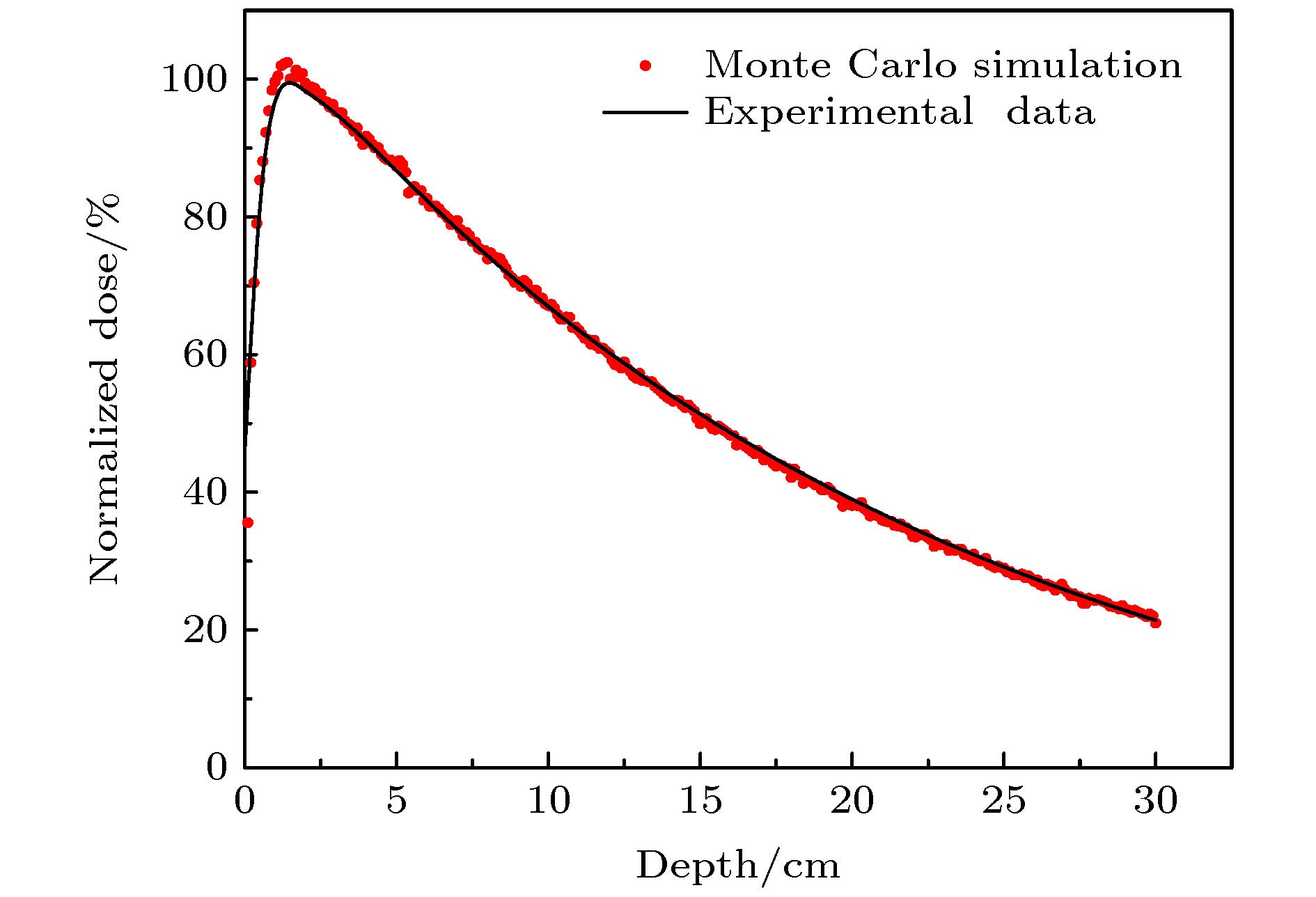
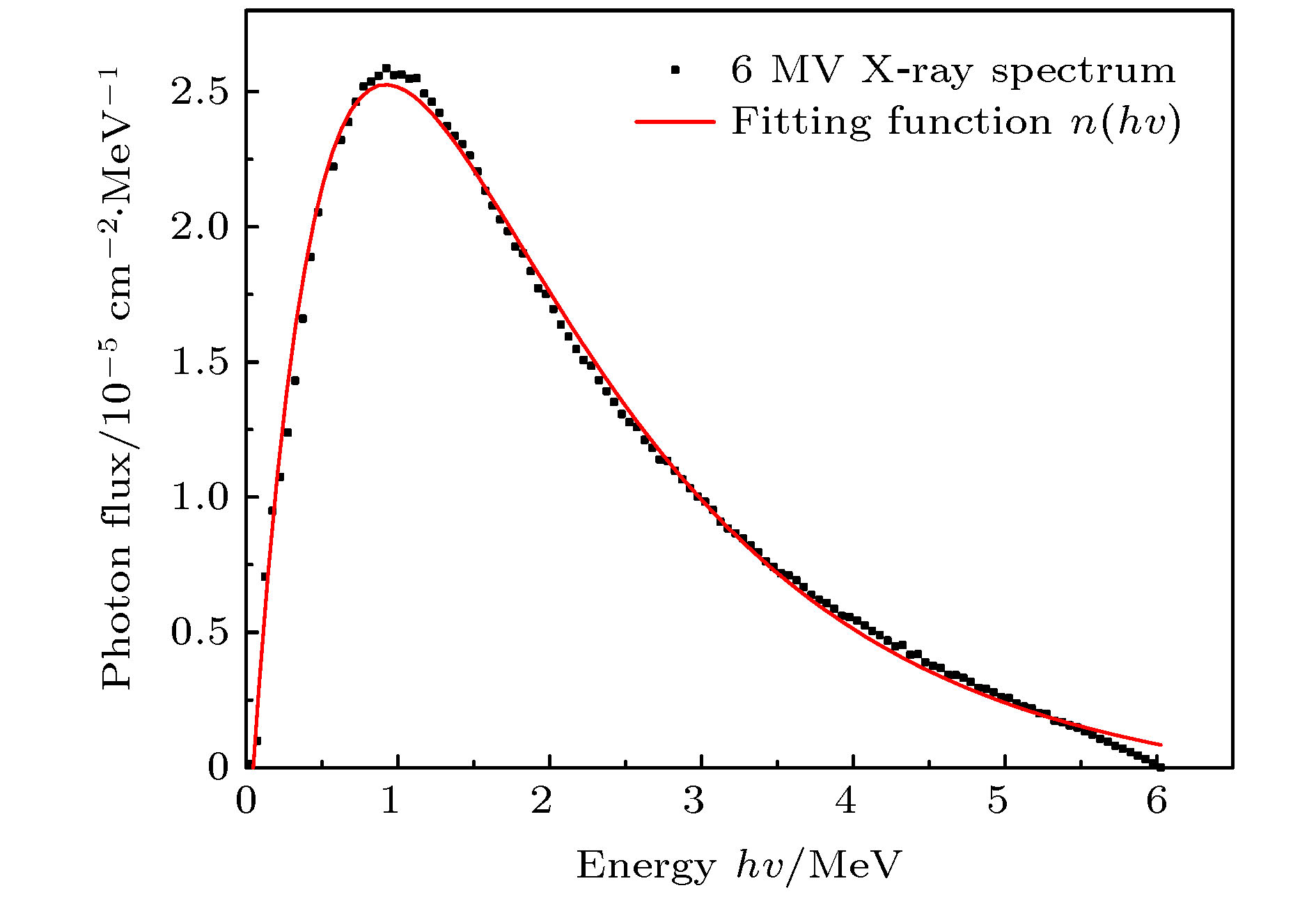
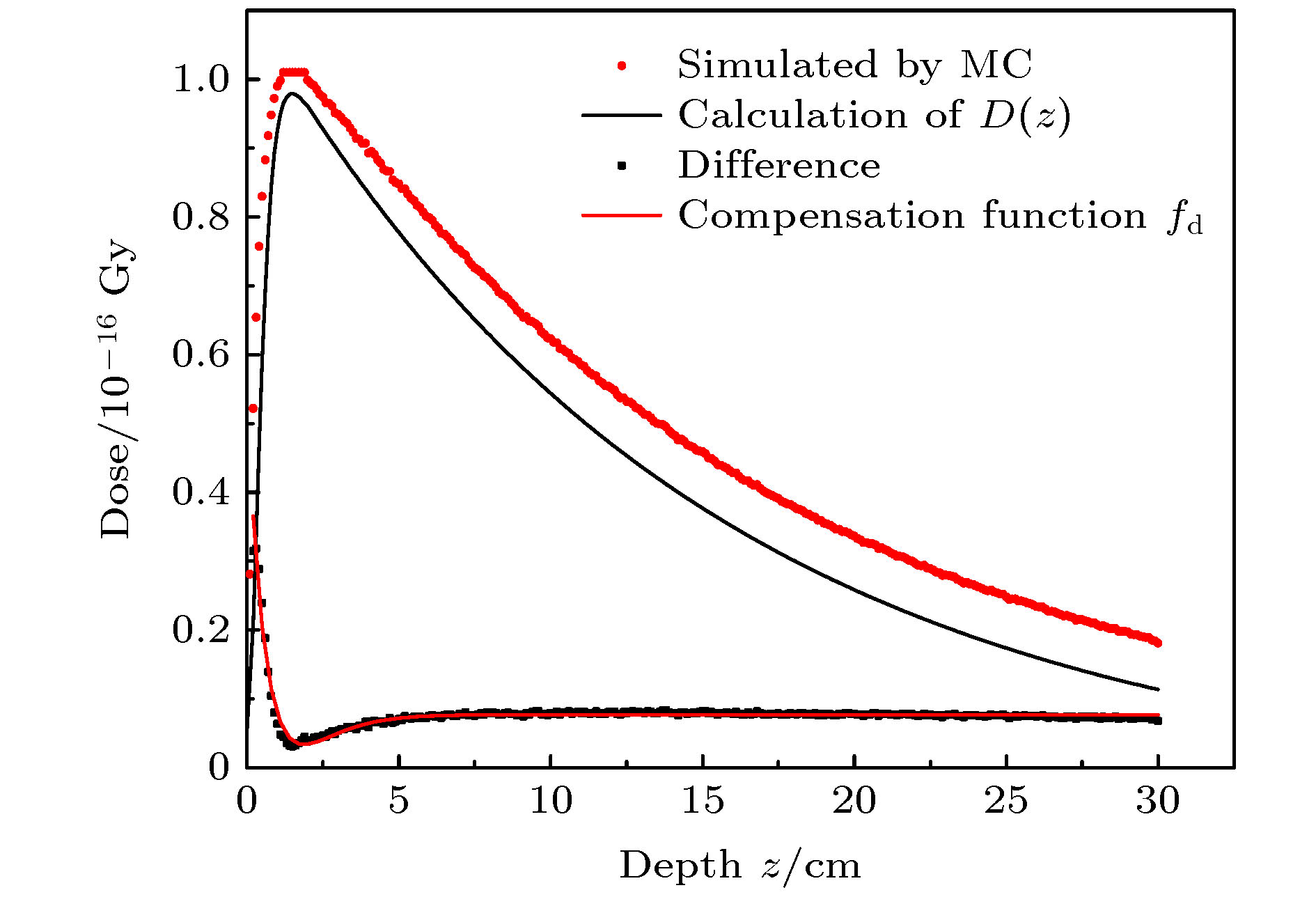
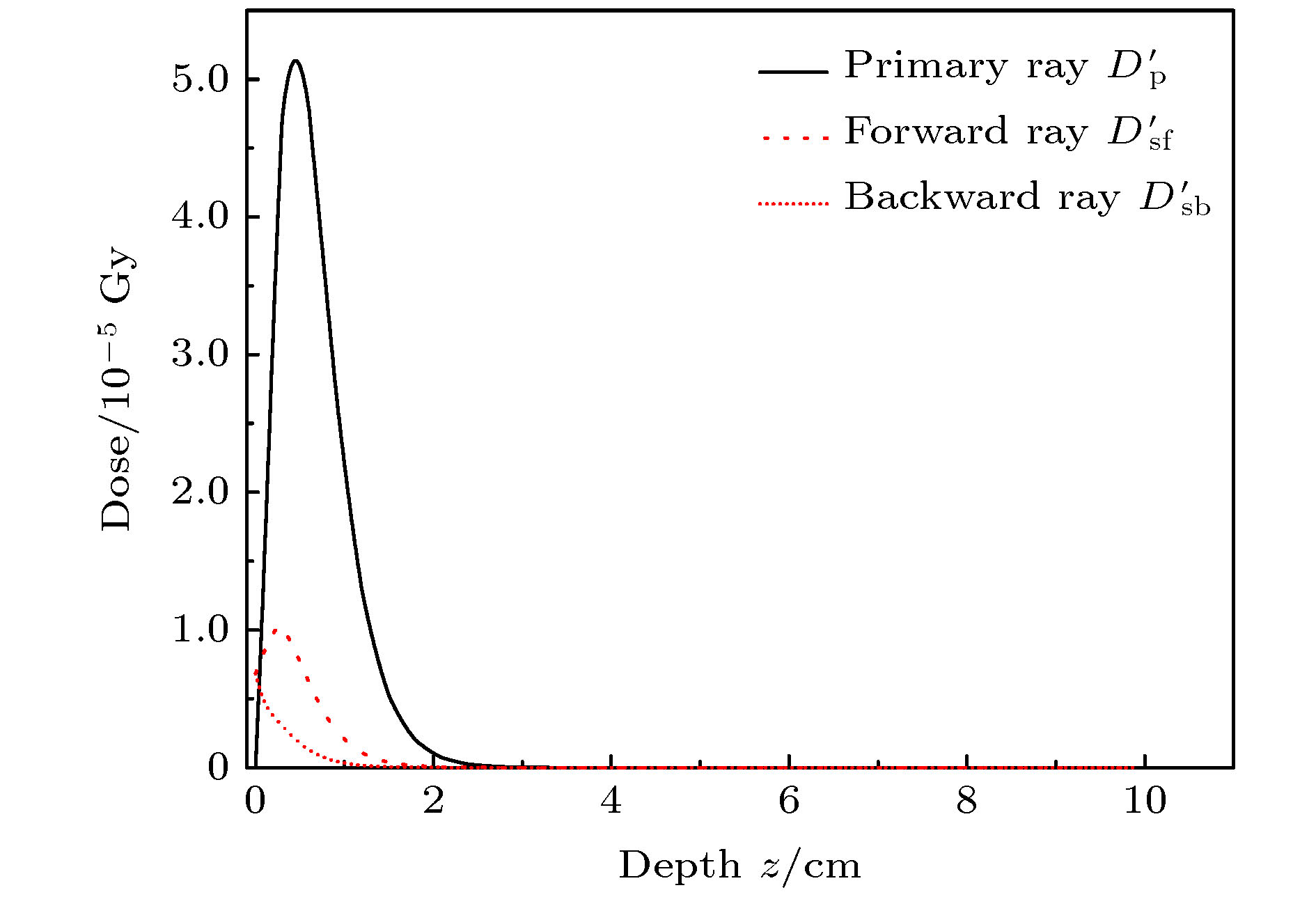
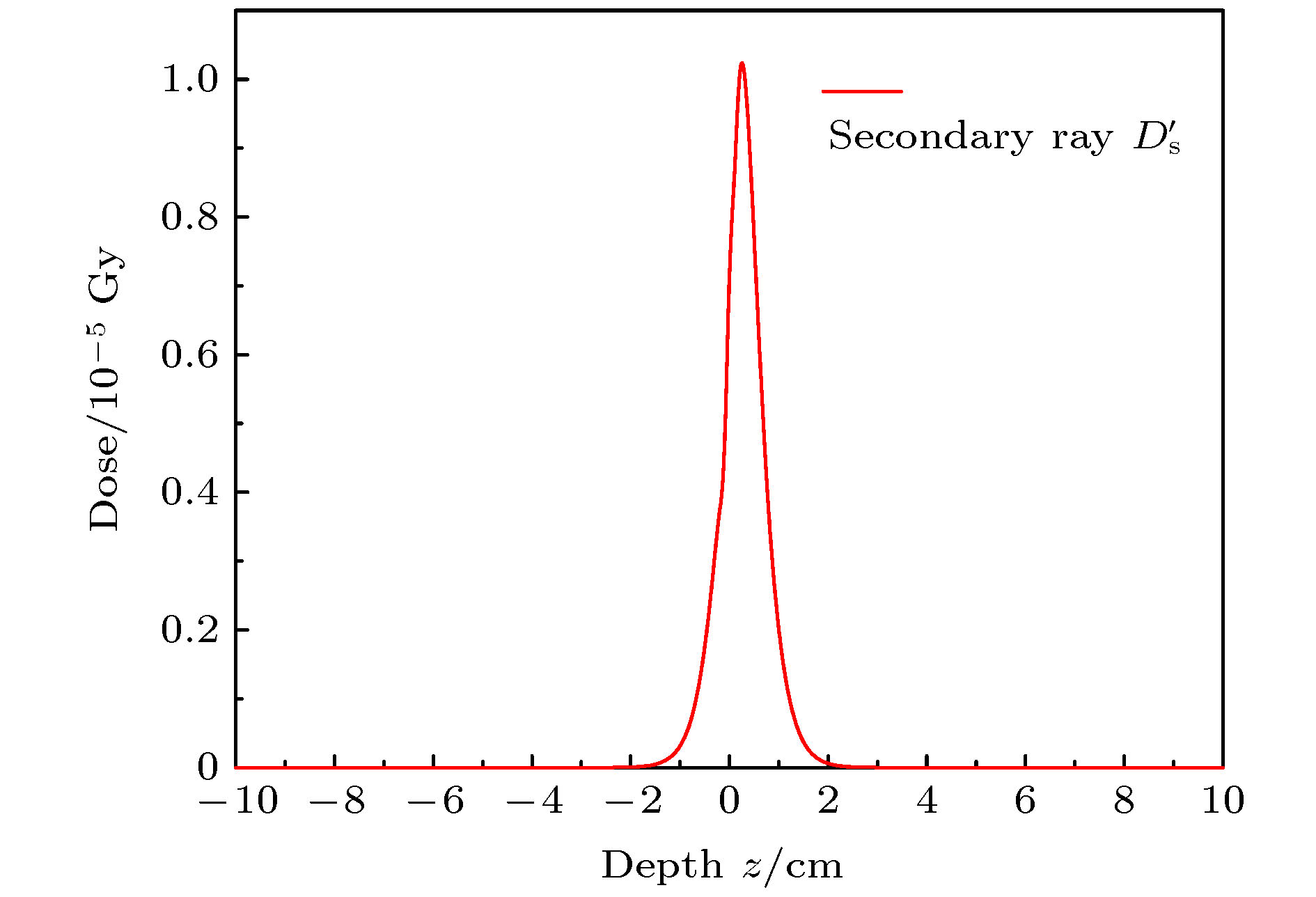
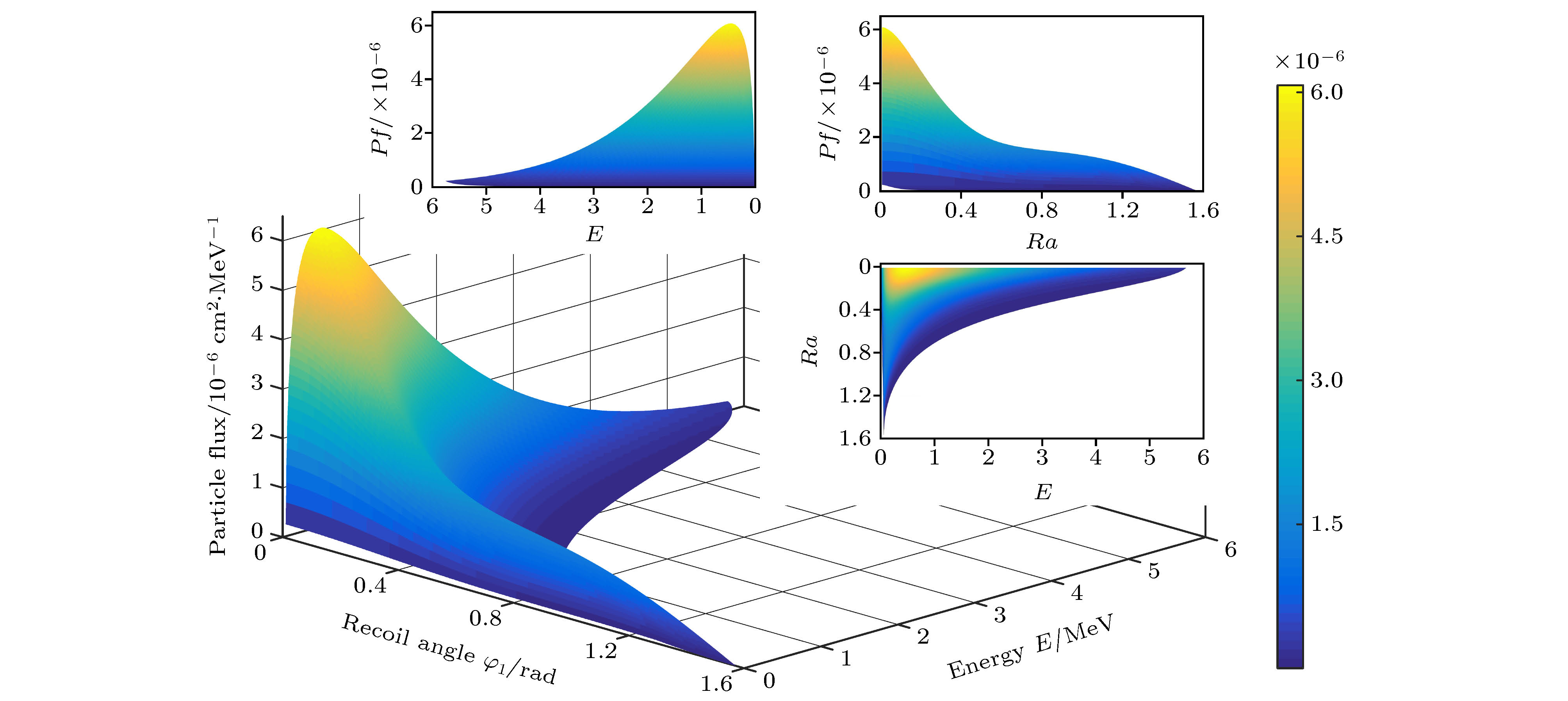
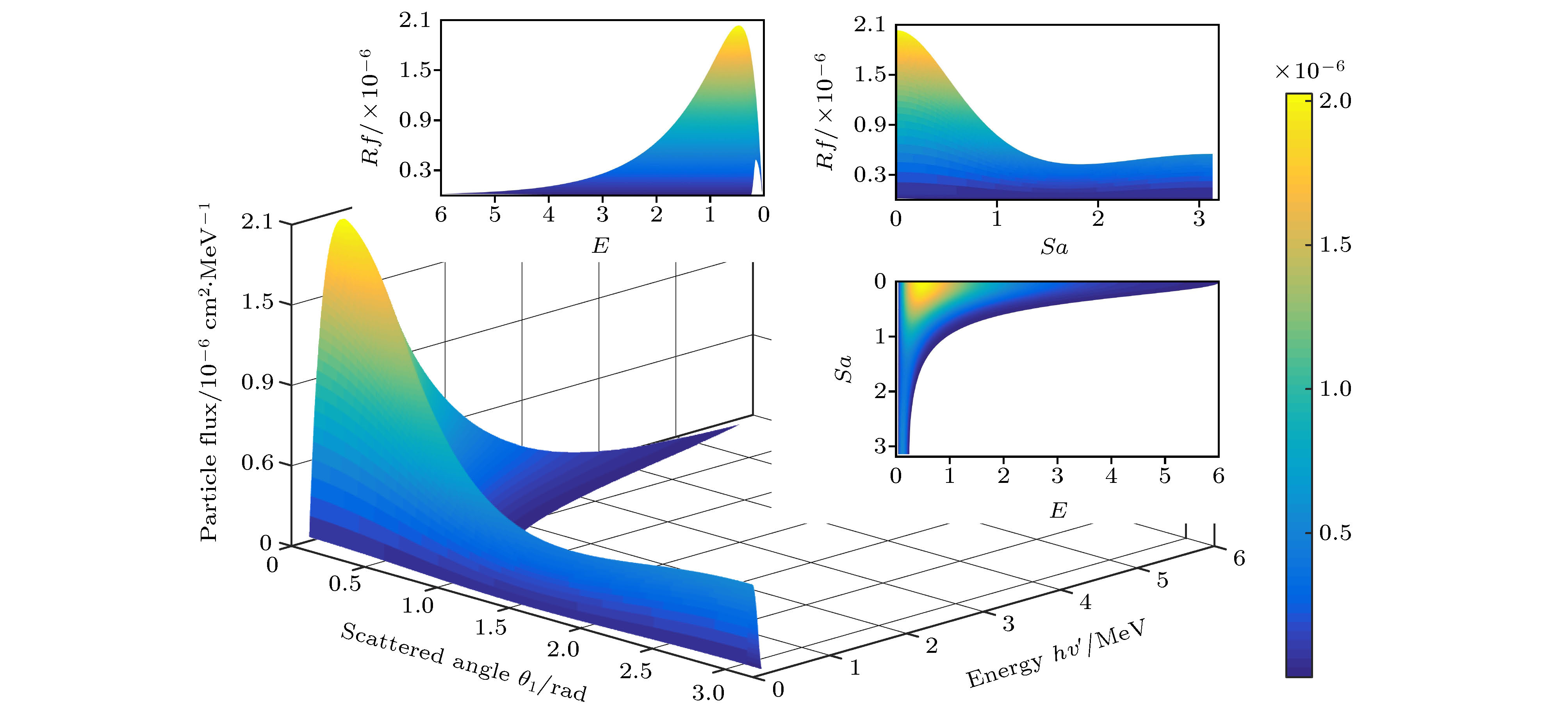
-
A algorithm of obtaining absolute dose at each tissue depth only by the mathematical calculation of formula is reported. The algorithm is based on integrating the energy flux of the electron generated by X-ray in the range of irradiation field, and the energy spectrum of ray and the secondary scattered ray are considered in this process. In this algorithm, the water phantom in the irradiation field is divided into several thin layers, and the energy flux of the electrons generated by interaction between the ray and thin layer reaching the calculation point is calculated. Finally, the absolute dose of the calculation point can be obtained by accumulating the energy flux contribution of all thin layers. For the X-ray with continuous energy spectrum, the expected mass attenuation coefficient is calculated for obtaining the photon flux at each depth in this process. The absolute dose calculated by this algorithm is verified by Monte Carlo simulation, and the difference between the algorithm and simulation is compensated for by a dose function about multiple scattering photons, and the function shows fast descent and then slow ascent. It is found that the ratio of the dose caused by backscatter to the surface dose, and the relationship among forward scatter, backward scatter and primary ray, and the relationship between the dose and the depth of the secondary scattered rays show a trend of first rising and then declining, and the depth of the peak value deviates from the position of the thin layer. Three-dimensional energy spectra of the secondary photon and the secondary electron are also compared with each other, and the spectrum is a function of particle flux about particle energy and particle direction. From the perspective of Compton effect, the physical meanings of different positions in the three-dimensional energy spectrum of the two particles are explained. It is found that the difference between algorithm percentage depth dose and simulation percentage depth dose is similar to the difference between small irradiation field percentage depth dose and big irradiation field percentage depth dose from simulation, and it is verified that the difference between algorithm and simulation comes from the increase of scattered rays. Finally, the algorithm is applied to the dose calculation of non-uniform phantom, which can accurately reflect the dose distribution characteristics and have less error.
-
Keywords:
- radiotherapy /
- model /
- absolute dose /
- Compton effect
[1] Yamamoto T, Mizowaki T, Miyabe Y, Takegawa H, Narita Y, Yano S, Nagata Y, Teshima T, Hiraoka M 2007 Phys. Med. Biol. 52 1991
Google Scholar
[2] Einstein A J, Henzlova M J, Rajagopalan S 2007 JAMA 298 317
Google Scholar
[3] Delaney G, Jacob S, Featherstone C, Barton M 2005 Cancers 104 1129
Google Scholar
[4] Das I J, Cheng C W, Watts R J, Ahnesjo A, Gibbons J, Li X A, Lowenstein J, Mitra R K, Simon W E, Zhu T C 2008 Med. Phys. 35 4186
Google Scholar
[5] van't Veld A A, van Luijk P, Praamstra F, van der Hulst P C 2001 Med. Phys. 28 738
Google Scholar
[6] van't Veld A A, van Luijk P, Praamstra F, van der Hulst P C 2000 Med. Phys. 27 923
Google Scholar
[7] Jette D 2000 Med. Phys. 27 1705
Google Scholar
[8] Jette D 1999 Med. Phys. 26 924
Google Scholar
[9] Tillikainen L, Helminen H, Torsti T, Siljamaki S, Alakuijala J, Pyyry J, Ulmer W 2008 Phys. Med. Biol. 53 3821
Google Scholar
[10] Jones A O, Das I J 2005 Med. Phys. 32 766
Google Scholar
[11] Aarup L R, Nahum A E, Zacharatou C, Juhler-Nottrup T, Knoos T, Nystrom H, Specht L, Wieslander E, Korreman S S 2009 Radiother. Oncol. 91 405
Google Scholar
[12] Krieger T, Sauer O A 2005 Phys. Med. Biol. 50 859
Google Scholar
[13] Beilla S, Younes T, Vieillevigne L, Bardies M, Franceries X, Simon L 2017 Phys. Medica 41 46
Google Scholar
[14] Jansen A A 1980 Icru Report 33: Radiation Quantities and Units (Washington)
[15] 胡逸民 1999 肿瘤放射物理学 (北京: 原子能出版社) 第38−44页
Hu Y M 1999 Radiation Oncology Physics (Beijing: Atomic Energy Press) pp38−44(in Chinese)
[16] Attix F H 1986 Gamma- and X-Ray Interactions in Matter (Vol.1) (Weinheim: Wiley-VCH Verlag GmbH & Co.KgaA) pp125−38
[17] Price M J, Hogstrom K R, Antolak J A, White R A, Bloch C D, Boyd R A 2007 J. Appl. Clin. Med. Phys 8 61
Google Scholar
[18] Malataras G, Kappas C, Lovelock D M J 2001 Phys. Med. Biol. 46 2435
Google Scholar
[19] Cheng C W, Cho S H, Taylor M, Das I J 2007 Med. Phys. 34 3149
Google Scholar
[20] Carlone M, Tadic T, Keller H, Rezaee M, Jaffray D 2016 Med. Phys. 43 2927
Google Scholar
[21] Kinhikar R A 2008 Technol. Cancer Res. Treat. 7 381
Google Scholar
[22] Chow J C L, Grigorov G N, Barnett R B 2006 Med. Dosim. 31 249
Google Scholar
[23] Disher B, Hajdok G, Gaede S, Battista J J 2012 Phys. Med. Biol. 57 1543
Google Scholar
[24] Mesbahi A, Dadgar H, Ghareh-Aghaji N, Mohammadzadeh M 2014 J. Cancer Res. Ther. 10 896
Google Scholar
-
图 1 绝对剂量的算法模型示意图
Figure 1. Schematic diagram of absolute dose algorithm model
图 2
$ {D}_{\mathrm{s}\mathrm{f}}' $ (a)和$ {D}_{\mathrm{s}\mathrm{b}}' $ (b)算法模型示意图Figure 2. Schematic diagram of
$ {D}_{\mathrm{s}\mathrm{f}}' $ (a) and$ {D}_{\mathrm{s}\mathrm{b}}' $ (b) algorithm model.
图 3 蒙特卡罗PDD与真实测量数据的对比
Figure 3. Comparison of PDD between Monte Carlo simulation and experimental data.
图 4 6 MV射线能谱及其仿真函数
Figure 4. 6 MV X-ray spectrum and its fitting function.
图 5 蒙特卡罗仿真的绝对剂量和计算绝对剂量
$ D\left(z\right) $ 的比较Figure 5. Comparison of absolute dose between Monte Carlo simulation and calculation of
$ D\left(z\right) $ .
图 6 比较由原射线产生的剂量
$ {D}_{p}' $ 、前向散射产生的剂量$ {D}_{\mathrm{s}\mathrm{f}}' $ 、后向散射产生的剂量$ {D}_{\mathrm{s}\mathrm{b}}' $ 随深度的变化Figure 6. Comparison of dose caused by primary ray
$ {D}_{\mathrm{p}}' $ , forward scatter$ {D}_{\mathrm{s}\mathrm{f}}' $ and backscatter$ {D}_{\mathrm{s}\mathrm{b}}' $ with depth.
图 7 向前和向后的二次射线产生的剂量随深度的变化
Figure 7. Dose caused by scattered ray in forward and back directions with depth.
图 8 二次电子的粒子注量随能量E和反冲角
$ {\varphi }_{1} $ 的变化Figure 8. Particle flux of secondary electron with energy E and recoil angle
$ {\varphi }_{1} $ .
图 9 二次光子的粒子注量随能量
$ {hv}' $ 和散射角${\theta _{\rm{1}}}$ 的变化Figure 9. Particle flux of secondary photon with energy
$ {hv}' $ and scattered angle$ {\theta }_{1} $ .
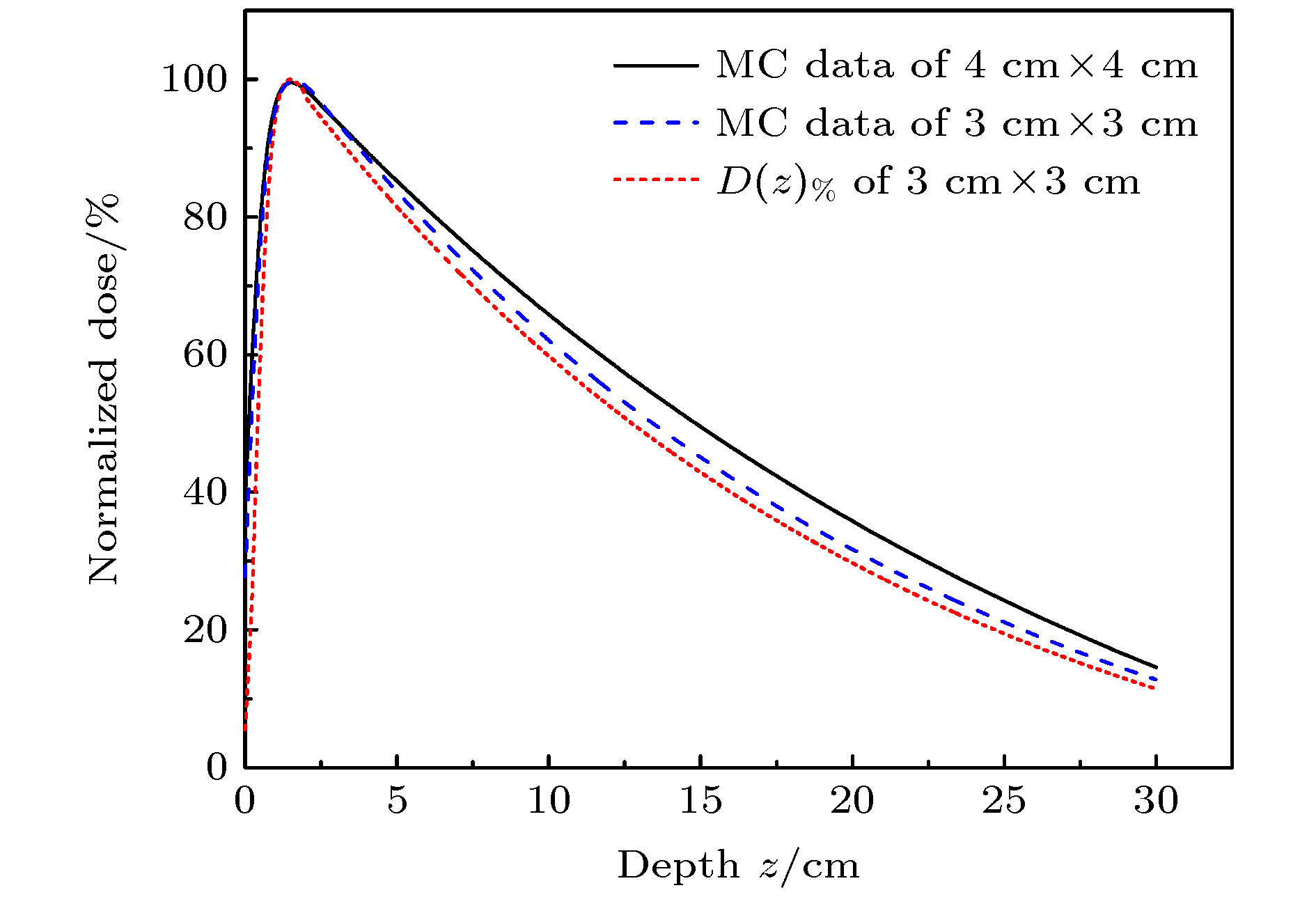
图 10 比较随不同射野(射野大小3 cm × 3 cm和4 cm × 4 cm)变化的蒙特卡罗仿真数据
$ {D}_{\mathrm{M}\mathrm{C}} $ 与计算的$ D{\left(z\right)}_{\%} $ (射野大小3 cm × 3 cm)Figure 10. Comparison of Monte Carlo simulation PDD with different fields (field size 3 cm × 3 cm and 4 cm × 4 cm) and calculation PDD
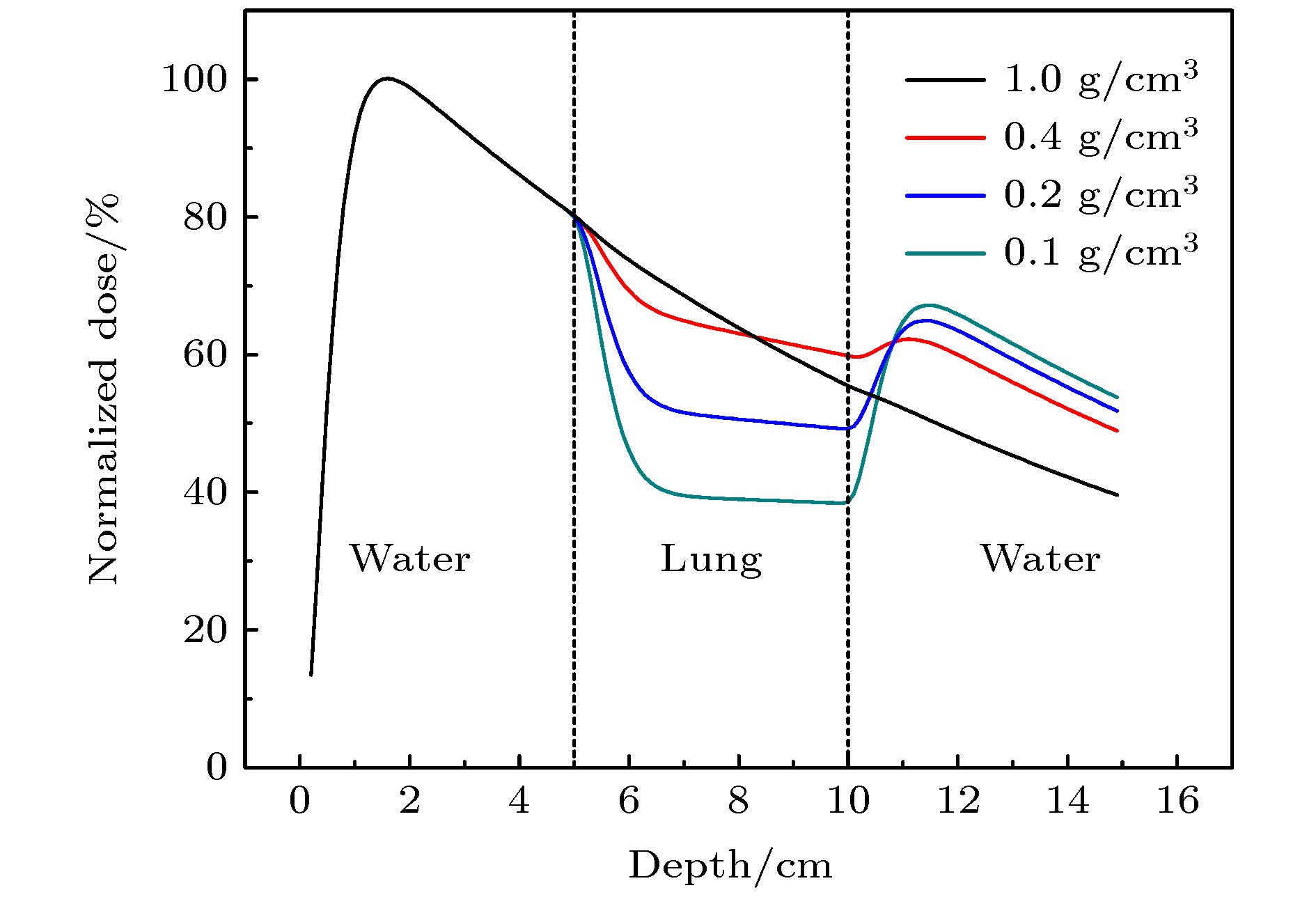
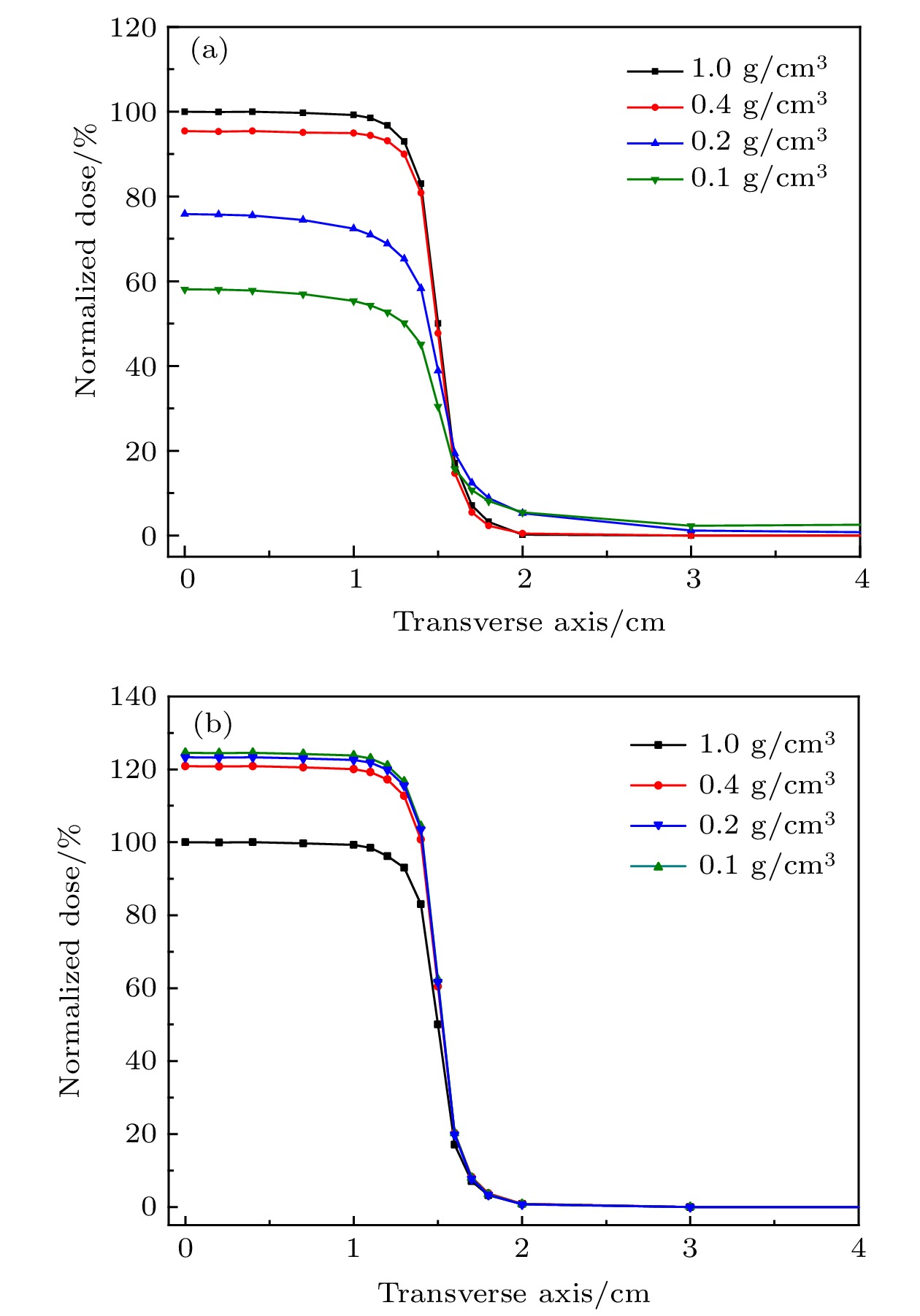
$ D{\left(z\right)}_{\%} $ (field size 3 cm × 3 cm).
图 11 不同肺密度的水肺水模体的射野中心轴百分深度剂量
Figure 11. Percentage depth dose of the central axis of the field of radiation in water-lung-water phantom with different lung densities.
图 12 不同模体深度处的离轴比曲线 (a) 7 cm; (b) 11 cm
Figure 12. Off-axis ratio curves at different phantom depths: (a) 7 cm; (b) 11 cm.
表 1 不同肺模体密度ρ对应参数kρ和μ0
Table 1. Parameters kρ and μ0 of lung phantom densities ρ.
ρ/g·cm–3 0.1 0.2 0.4 ≥ ρT kρ –6 –3.75 0.75 3 μ0 6.8 6.1 4.7 4 
DownLoad: CSV
-
[1] Yamamoto T, Mizowaki T, Miyabe Y, Takegawa H, Narita Y, Yano S, Nagata Y, Teshima T, Hiraoka M 2007 Phys. Med. Biol. 52 1991
Google Scholar
[2] Einstein A J, Henzlova M J, Rajagopalan S 2007 JAMA 298 317
Google Scholar
[3] Delaney G, Jacob S, Featherstone C, Barton M 2005 Cancers 104 1129
Google Scholar
[4] Das I J, Cheng C W, Watts R J, Ahnesjo A, Gibbons J, Li X A, Lowenstein J, Mitra R K, Simon W E, Zhu T C 2008 Med. Phys. 35 4186
Google Scholar
[5] van't Veld A A, van Luijk P, Praamstra F, van der Hulst P C 2001 Med. Phys. 28 738
Google Scholar
[6] van't Veld A A, van Luijk P, Praamstra F, van der Hulst P C 2000 Med. Phys. 27 923
Google Scholar
[7] Jette D 2000 Med. Phys. 27 1705
Google Scholar
[8] Jette D 1999 Med. Phys. 26 924
Google Scholar
[9] Tillikainen L, Helminen H, Torsti T, Siljamaki S, Alakuijala J, Pyyry J, Ulmer W 2008 Phys. Med. Biol. 53 3821
Google Scholar
[10] Jones A O, Das I J 2005 Med. Phys. 32 766
Google Scholar
[11] Aarup L R, Nahum A E, Zacharatou C, Juhler-Nottrup T, Knoos T, Nystrom H, Specht L, Wieslander E, Korreman S S 2009 Radiother. Oncol. 91 405
Google Scholar
[12] Krieger T, Sauer O A 2005 Phys. Med. Biol. 50 859
Google Scholar
[13] Beilla S, Younes T, Vieillevigne L, Bardies M, Franceries X, Simon L 2017 Phys. Medica 41 46
Google Scholar
[14] Jansen A A 1980 Icru Report 33: Radiation Quantities and Units (Washington)
[15] 胡逸民 1999 肿瘤放射物理学 (北京: 原子能出版社) 第38−44页
Hu Y M 1999 Radiation Oncology Physics (Beijing: Atomic Energy Press) pp38−44(in Chinese)
[16] Attix F H 1986 Gamma- and X-Ray Interactions in Matter (Vol.1) (Weinheim: Wiley-VCH Verlag GmbH & Co.KgaA) pp125−38
[17] Price M J, Hogstrom K R, Antolak J A, White R A, Bloch C D, Boyd R A 2007 J. Appl. Clin. Med. Phys 8 61
Google Scholar
[18] Malataras G, Kappas C, Lovelock D M J 2001 Phys. Med. Biol. 46 2435
Google Scholar
[19] Cheng C W, Cho S H, Taylor M, Das I J 2007 Med. Phys. 34 3149
Google Scholar
[20] Carlone M, Tadic T, Keller H, Rezaee M, Jaffray D 2016 Med. Phys. 43 2927
Google Scholar
[21] Kinhikar R A 2008 Technol. Cancer Res. Treat. 7 381
Google Scholar
[22] Chow J C L, Grigorov G N, Barnett R B 2006 Med. Dosim. 31 249
Google Scholar
[23] Disher B, Hajdok G, Gaede S, Battista J J 2012 Phys. Med. Biol. 57 1543
Google Scholar
[24] Mesbahi A, Dadgar H, Ghareh-Aghaji N, Mohammadzadeh M 2014 J. Cancer Res. Ther. 10 896
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8029
- PDF Downloads: 114
- Cited By: 0
