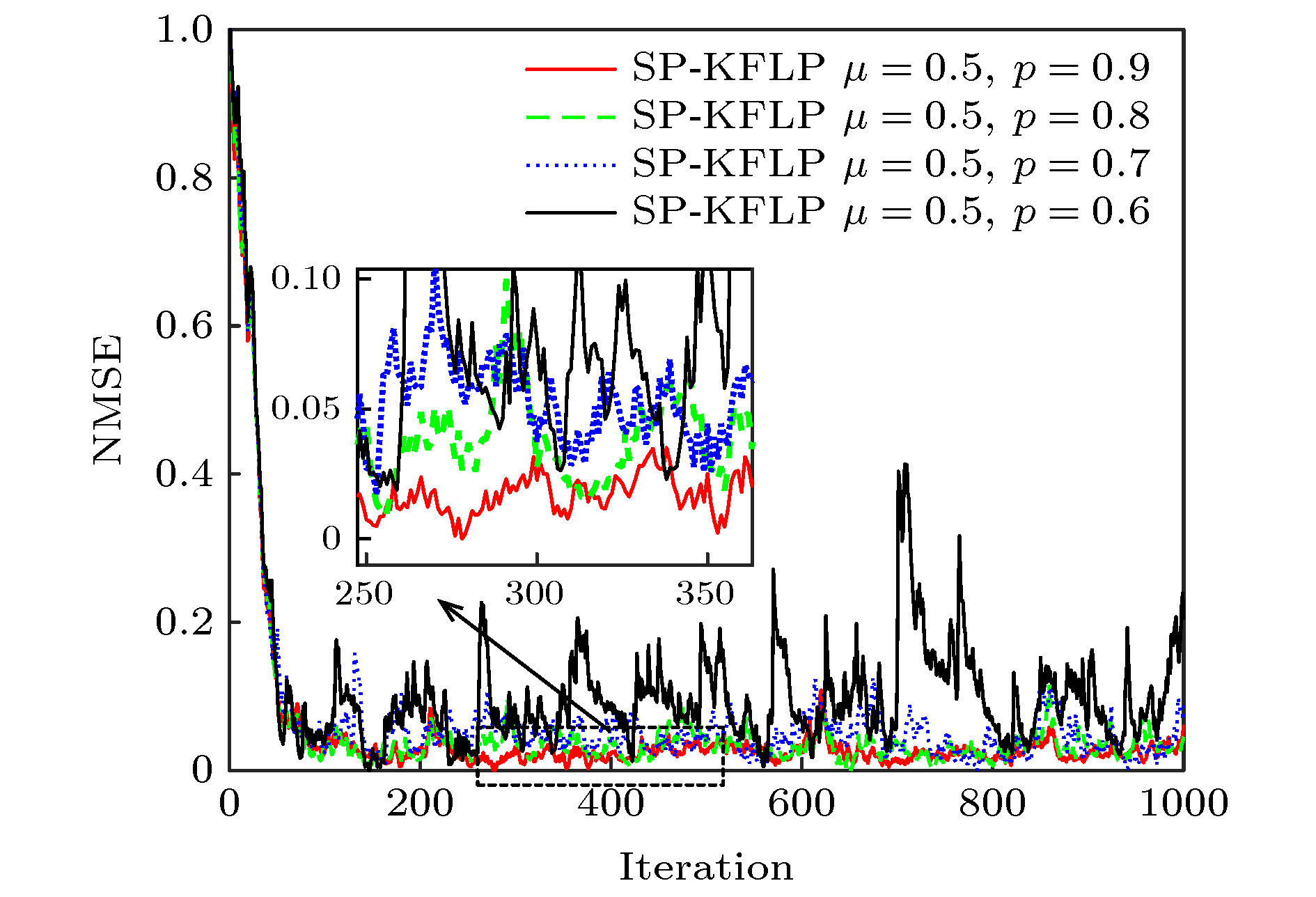
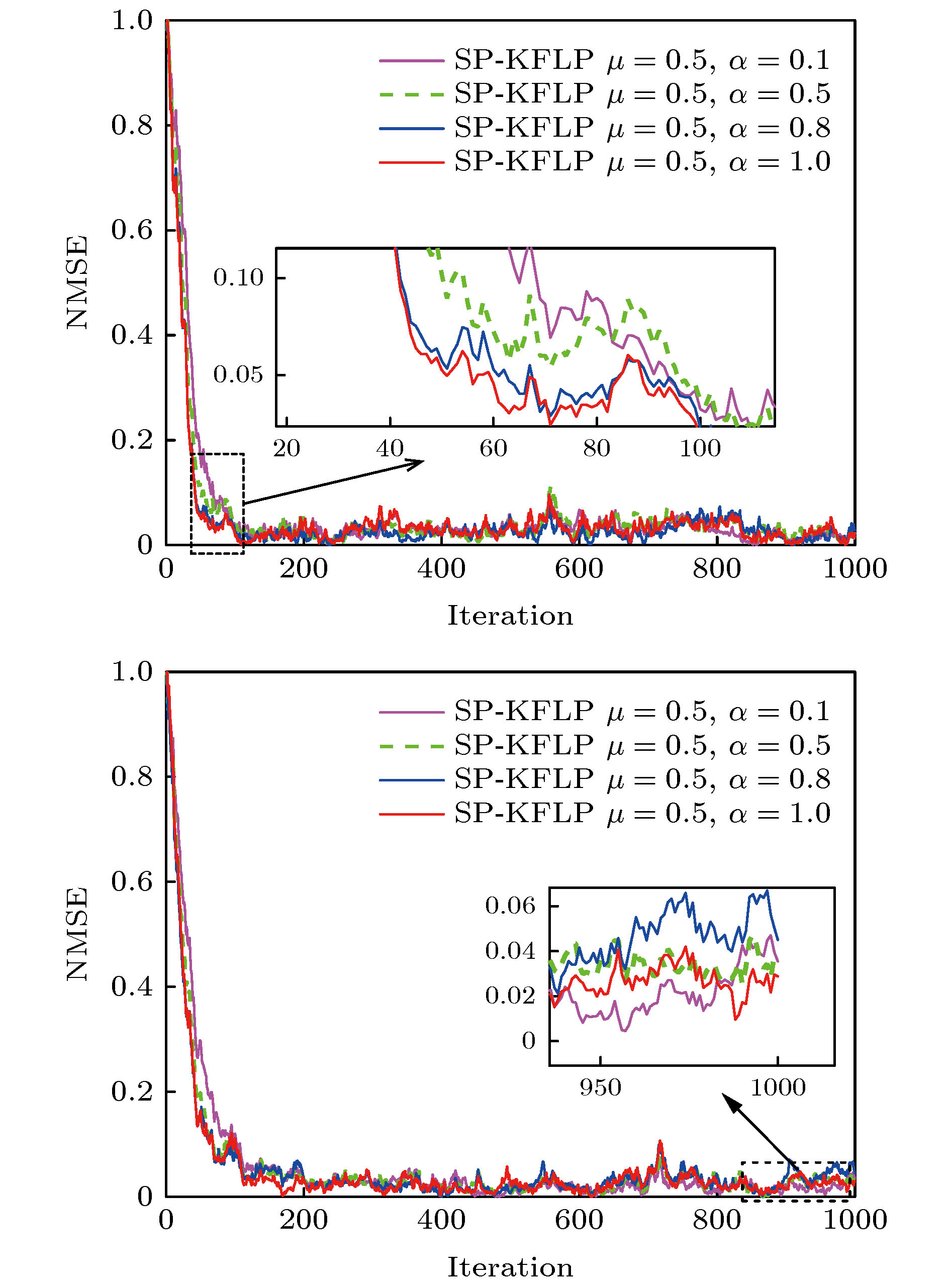
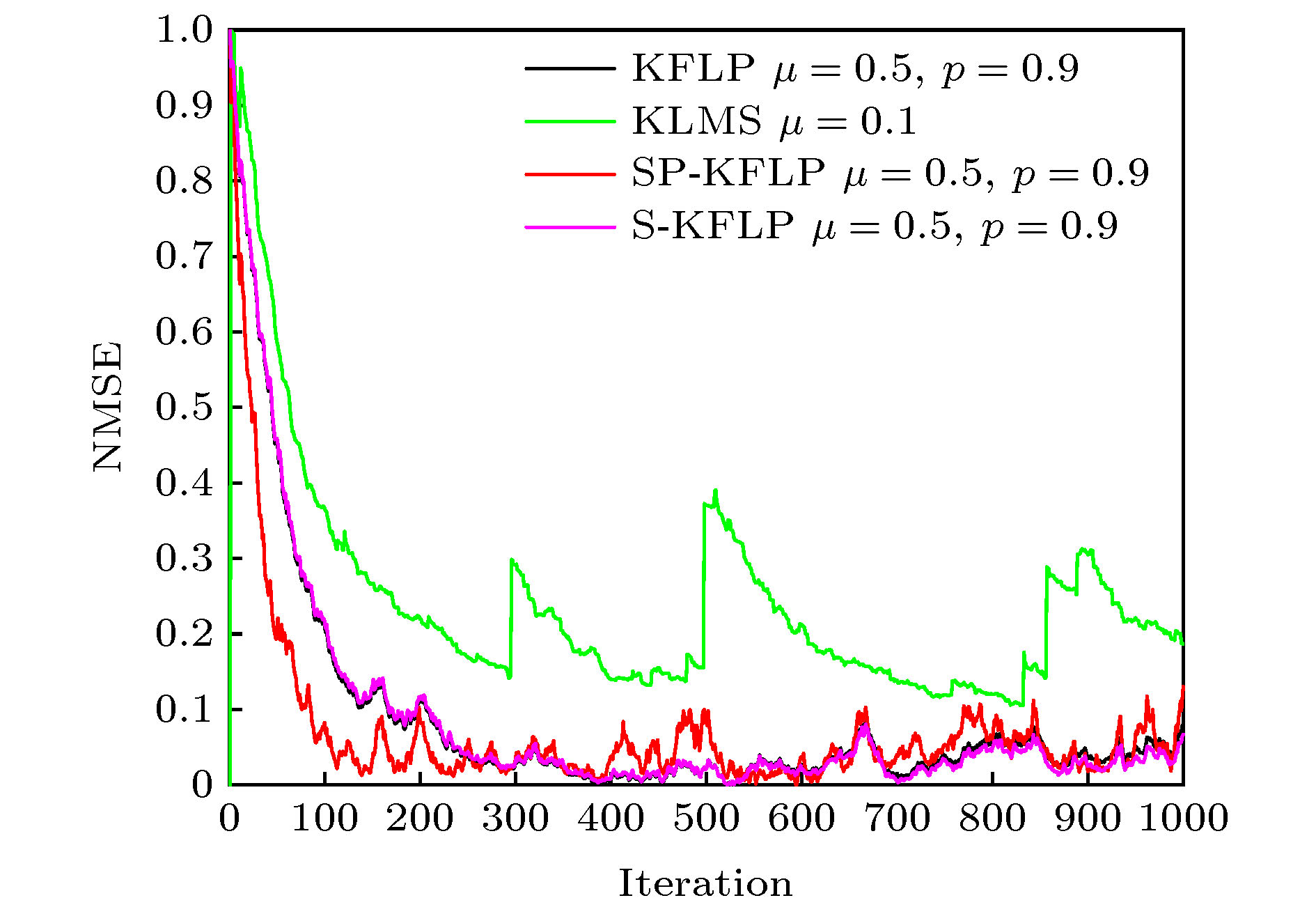
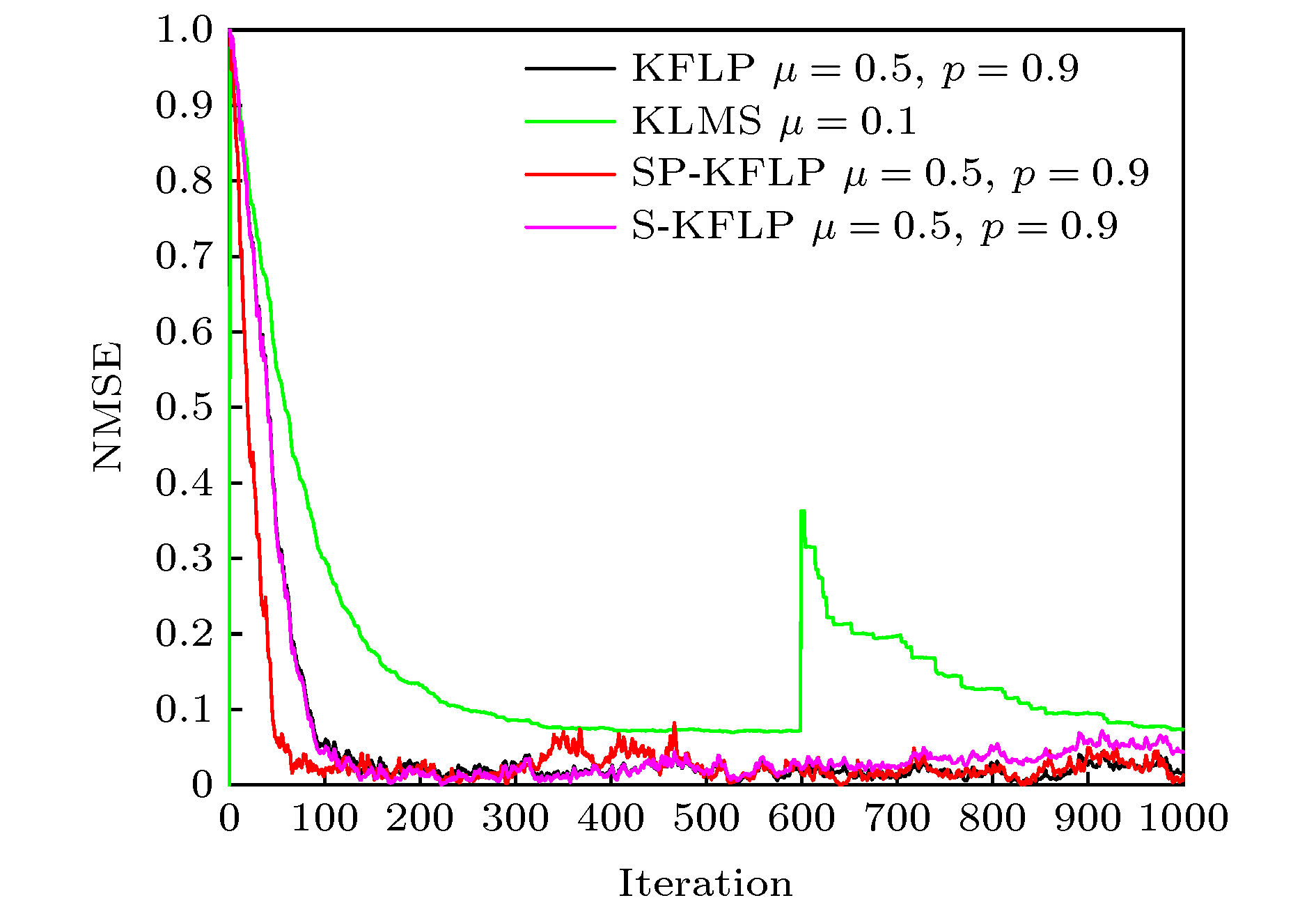
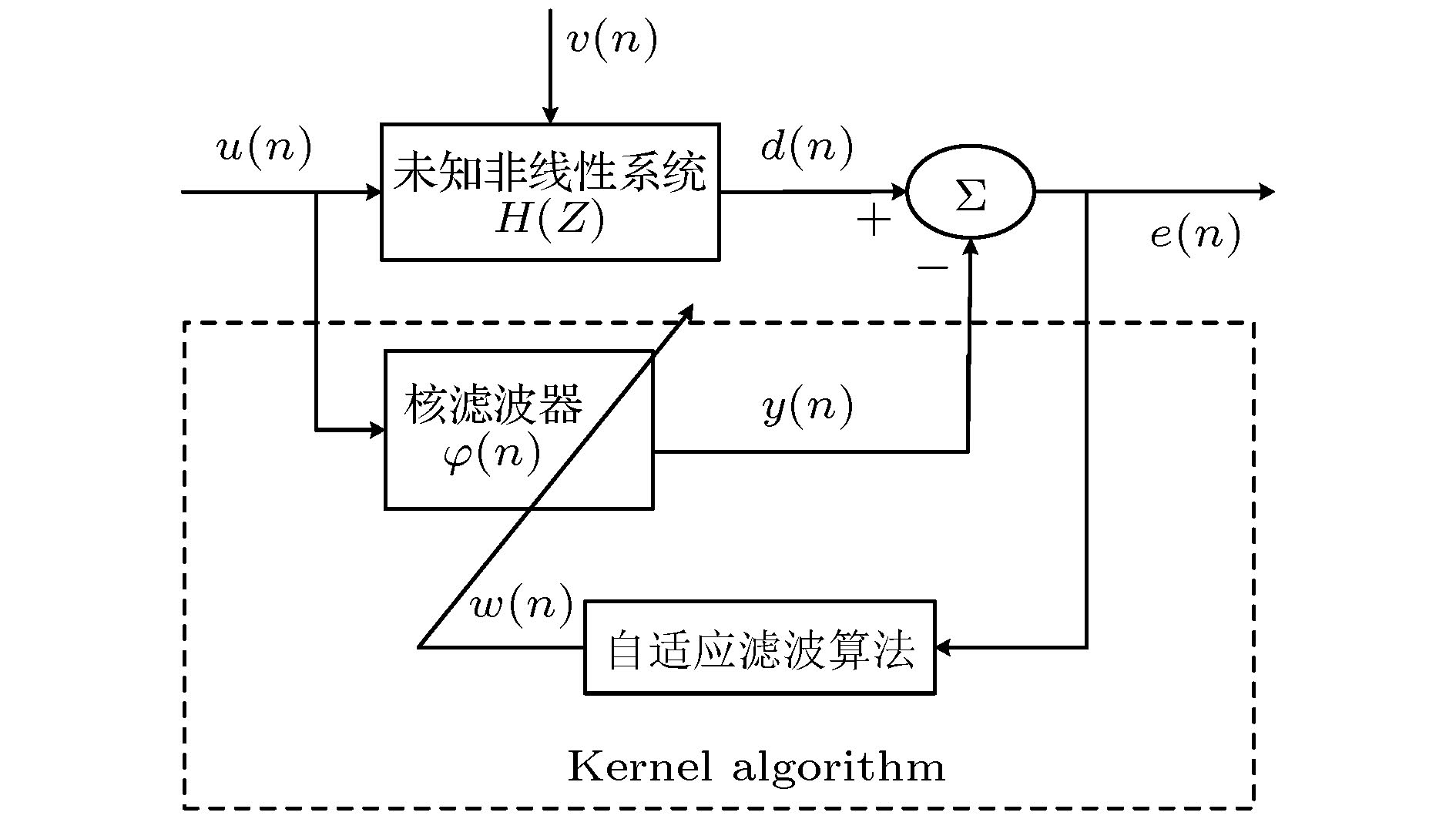
-
Kernel adaptive filters are a class of powerful nonlinear filter developed in reproducing kernel Hilbert space (RKHS).The Gaussian kernel is usually the default kernel in KAF algorithm, because the Gaussian kernel has the universal approximation. However, in previous research the kernel adaptive filtering algorithms were mostly based on mean square error criterion and assumed to be in a Gaussian noise environment. When environmental noise is changed, the performance of conventional kernel adaptive filtering algorithm based on mean square error criterion is seriously reduced to failure due to the interference of non-Gaussian noise and the influence of inappropriate non-Gaussian modeling. Therefore, it is important to develop a new method of suppressing the noise of non-Gaussian signals. In this paper, a new kernel fractional lower power adaptive filtering algorithm is proposed by combining the benefits of the kernel method and a new loss function which is robust against non-Gaussian impulsive interferences and has fast convergence under a similar stability condition. The proposed SP-KFLP algorithm generates a new framework of cost function which combines the Softplus function with the KFLP algorithm by updating its weight vector according to the gradient estimation while nonlinear saturation characteristics of output error are used. Compared with the features of sigmoid function the features of the Softplus function guarantee the SP-KFLP an excellent performance for combatting impulsive interference and speeding up the convergence rate. In the kernel fractional low power criterion the reciprocal of the system error is used as the coefficient of the weight vector update formula, and the method of error burst is used to make the weight vector not update to resist the impulse noise. The mean square convergence analysis for SP-KFLP is conducted, and a sufficient condition for guaranteeing convergence is therefore obtained by using the energy conservation relation. The proposed algorithm is very simple computationally. Simulations in a system identification show that the proposed SP-KFLP algorithm outperforms the kernel least-mean-square algorithm, kernel fractional lower power algorithm, and sigmoid kernel fractional lower algorithm in terms of convergence rate and the robustness of against impulsive interference. The proposed algorithm improves not only the capability of resisting impulsive interference, but also the convergence rate. In other words, the contradiction between convergence and tracking performance stability is well taken into account, and the performance under Gaussian noise is also better than the performance of the traditional kernel adaptive algorithm.
-
Keywords:
- kernel adaptive filtering algorithm /
- Softplus function /
- kernel fractional low power error criterion /
- non-Gaussian impulse interference
[1] Huang F Y, Zhang J S 2017 Digital Signal Process. 70 49
Google Scholar
[2] Wiener N 1958 Nonlinear Problems in Random Theory (New York: Wiley) pp45−145
[3] Gabor D 1968 Nature 217 584
Google Scholar
[4] Wang W, Zhao H, Chen B 2017 Circuits Syst. Signal Process. 36 4097
Google Scholar
[5] 沈力华, 陈吉红, 曾志刚, 金健 2018 67 030501
Google Scholar
Shen L H, Chen J H, Zeng Z G, Jin J 2018 Acta Phys. Sin. 67 030501
Google Scholar
[6] Frieb T, Harrison R F 1999 Intell. Data Anal. 3 307
Google Scholar
[7] Liu W, Pokharel P P, Príncipe J C 2008 IEEE Trans. Signal Process. 56 543
Google Scholar
[8] Engel Y, Mannor S, Meir R 2004 IEEE Trans. Signal Process. 52 2275
Google Scholar
[9] Liu W, Park I, Wang Y, Príncipe J C 2009 IEEE Signal Process. 57 3801
Google Scholar
[10] 李军, 后新燕 2019 68 100503
Google Scholar
Li J, Hou X Y 2019 Acta Phys. Sin. 68 100503
Google Scholar
[11] Zhao H Q, Lu L, Chen B D 2017 Nonlinear Dyn. 90 999
Google Scholar
[12] Vaerenbergh S V, Lazaro-Gredilla M, Santurmaria 2012 IEEE Trans. Neural Networks Learn. 23 1313
Google Scholar
[13] Wang S, Wang W, Duan S 2017 IEEE Trans. Circuits Syst. Express Briefs 64 730
Google Scholar
[14] Zhang T, Wang S Y, Zhang H N, Xiong K, Wang L 2019 Entropy 21 588
Google Scholar
[15] 林飞飞, 曾喆昭 2017 66 090504
Google Scholar
Lin F F, Zeng J Z 2017 Acta Phys. Sin. 66 090504
Google Scholar
[16] Gao W, En J 2017 IEEE Signal Process. Lett. 24 996
Google Scholar
[17] Dai S G, Jin M M 2020 Int. J. Pattern Recognit 34 2054006
Google Scholar
[18] 李群生, 赵剡, 寇磊, 王进达 2020 电子与信息学报 42 924
Li Q S, Zhao Y, Kou L, Wang J D 2020 J. Electr. Inf. Technol. 42 (in Chinesse)
[19] 董庆, 林云 2019 计算机科学 46 80
Google Scholar
Dong Q, Lin Y 2019 Computer Science 46 80
Google Scholar
[20] Pei S C, Tseng C C 1994 IEEE J. Sel. Areas Commun. 12 1540
Google Scholar
[21] Zhao J, Zhang H B, Liao X F 2018 Digital Signal Process. 83 59
Google Scholar
[22] Zhao J, Zhang H B, Andrew Zhang J 2020 Signal Process. 166 107270
Google Scholar
-
图 1 系统识别模型
Figure 1. System identification model.
图 2 非高斯噪声下, 不同p值的SP-KFLP算法归一化学习曲线对比
Figure 2. Comparison of normalized learning curves of SP-KFLP algorithm with different p values under non-Gaussian noise.
图 3 不同
$\alpha $ 值下SP-KFLP算法的归一化学习曲线对比Figure 3. Comparison of normalized learning curves of SP-KFLP algorithm under different values
$\alpha $ .
图 4 KLMS, KMCC, KFLP, S-FKLP和本文SP-KFLP算法的比较
Figure 4. Comparison of KLMS, KMCC, KFLP, S-FKLP and SP-KFLP algorithms in this paper.
图 5 非高斯干扰下的KFLP, KLMS, S-KFLP与SP-KFLP算法比较
Figure 5. Comparison of KFLP, KLMS, S-KFLP and SP-KFLP algorithms under non-Gaussian interference.
图 6 在第600次迭代过程中加入冲激噪声时各算法性能对比
Figure 6. Performance comparison of algorithms when impulsive noise is added in the 600th iteration.
-
[1] Huang F Y, Zhang J S 2017 Digital Signal Process. 70 49
Google Scholar
[2] Wiener N 1958 Nonlinear Problems in Random Theory (New York: Wiley) pp45−145
[3] Gabor D 1968 Nature 217 584
Google Scholar
[4] Wang W, Zhao H, Chen B 2017 Circuits Syst. Signal Process. 36 4097
Google Scholar
[5] 沈力华, 陈吉红, 曾志刚, 金健 2018 67 030501
Google Scholar
Shen L H, Chen J H, Zeng Z G, Jin J 2018 Acta Phys. Sin. 67 030501
Google Scholar
[6] Frieb T, Harrison R F 1999 Intell. Data Anal. 3 307
Google Scholar
[7] Liu W, Pokharel P P, Príncipe J C 2008 IEEE Trans. Signal Process. 56 543
Google Scholar
[8] Engel Y, Mannor S, Meir R 2004 IEEE Trans. Signal Process. 52 2275
Google Scholar
[9] Liu W, Park I, Wang Y, Príncipe J C 2009 IEEE Signal Process. 57 3801
Google Scholar
[10] 李军, 后新燕 2019 68 100503
Google Scholar
Li J, Hou X Y 2019 Acta Phys. Sin. 68 100503
Google Scholar
[11] Zhao H Q, Lu L, Chen B D 2017 Nonlinear Dyn. 90 999
Google Scholar
[12] Vaerenbergh S V, Lazaro-Gredilla M, Santurmaria 2012 IEEE Trans. Neural Networks Learn. 23 1313
Google Scholar
[13] Wang S, Wang W, Duan S 2017 IEEE Trans. Circuits Syst. Express Briefs 64 730
Google Scholar
[14] Zhang T, Wang S Y, Zhang H N, Xiong K, Wang L 2019 Entropy 21 588
Google Scholar
[15] 林飞飞, 曾喆昭 2017 66 090504
Google Scholar
Lin F F, Zeng J Z 2017 Acta Phys. Sin. 66 090504
Google Scholar
[16] Gao W, En J 2017 IEEE Signal Process. Lett. 24 996
Google Scholar
[17] Dai S G, Jin M M 2020 Int. J. Pattern Recognit 34 2054006
Google Scholar
[18] 李群生, 赵剡, 寇磊, 王进达 2020 电子与信息学报 42 924
Li Q S, Zhao Y, Kou L, Wang J D 2020 J. Electr. Inf. Technol. 42 (in Chinesse)
[19] 董庆, 林云 2019 计算机科学 46 80
Google Scholar
Dong Q, Lin Y 2019 Computer Science 46 80
Google Scholar
[20] Pei S C, Tseng C C 1994 IEEE J. Sel. Areas Commun. 12 1540
Google Scholar
[21] Zhao J, Zhang H B, Liao X F 2018 Digital Signal Process. 83 59
Google Scholar
[22] Zhao J, Zhang H B, Andrew Zhang J 2020 Signal Process. 166 107270
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5663
- PDF Downloads: 61
- Cited By: 0
