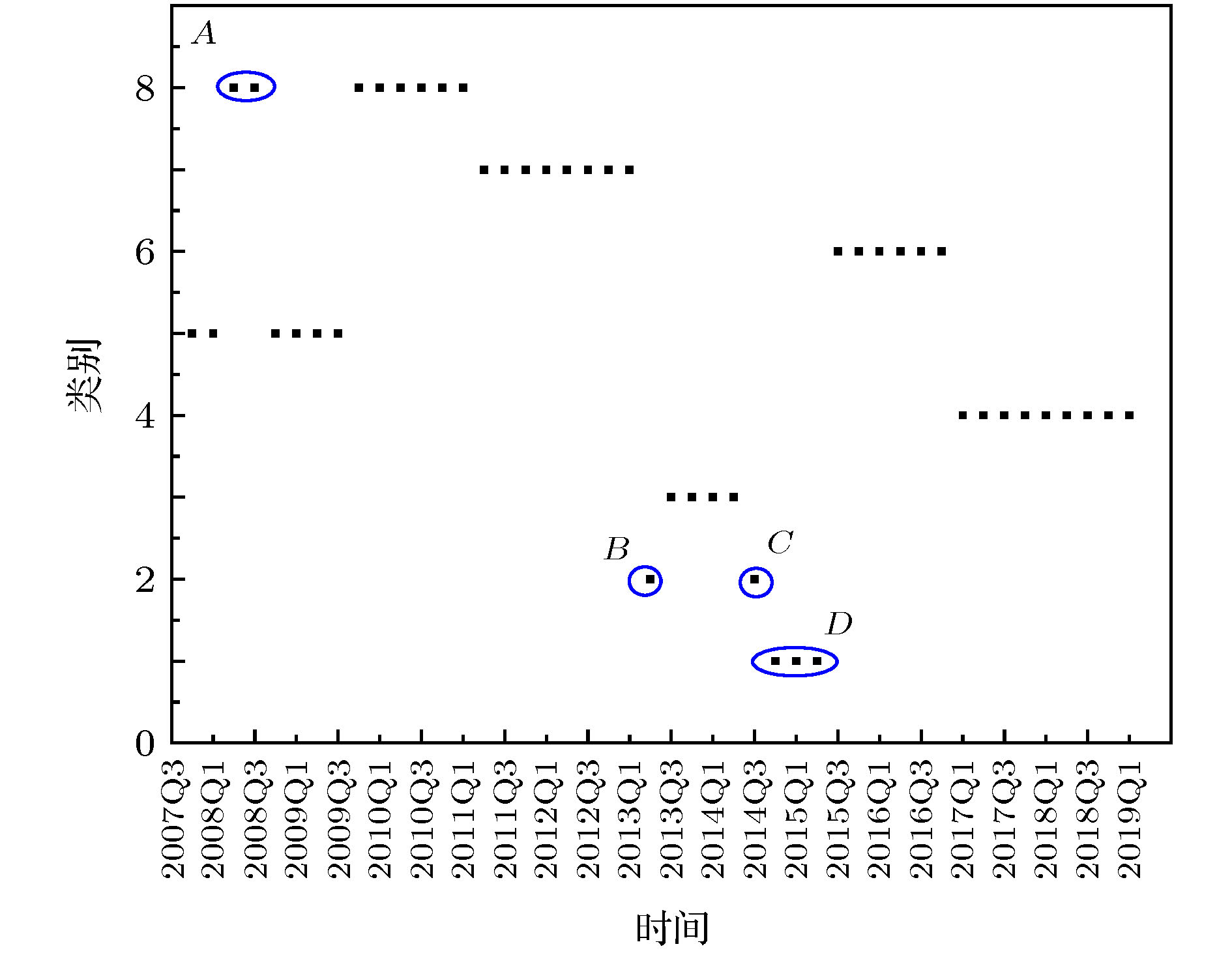
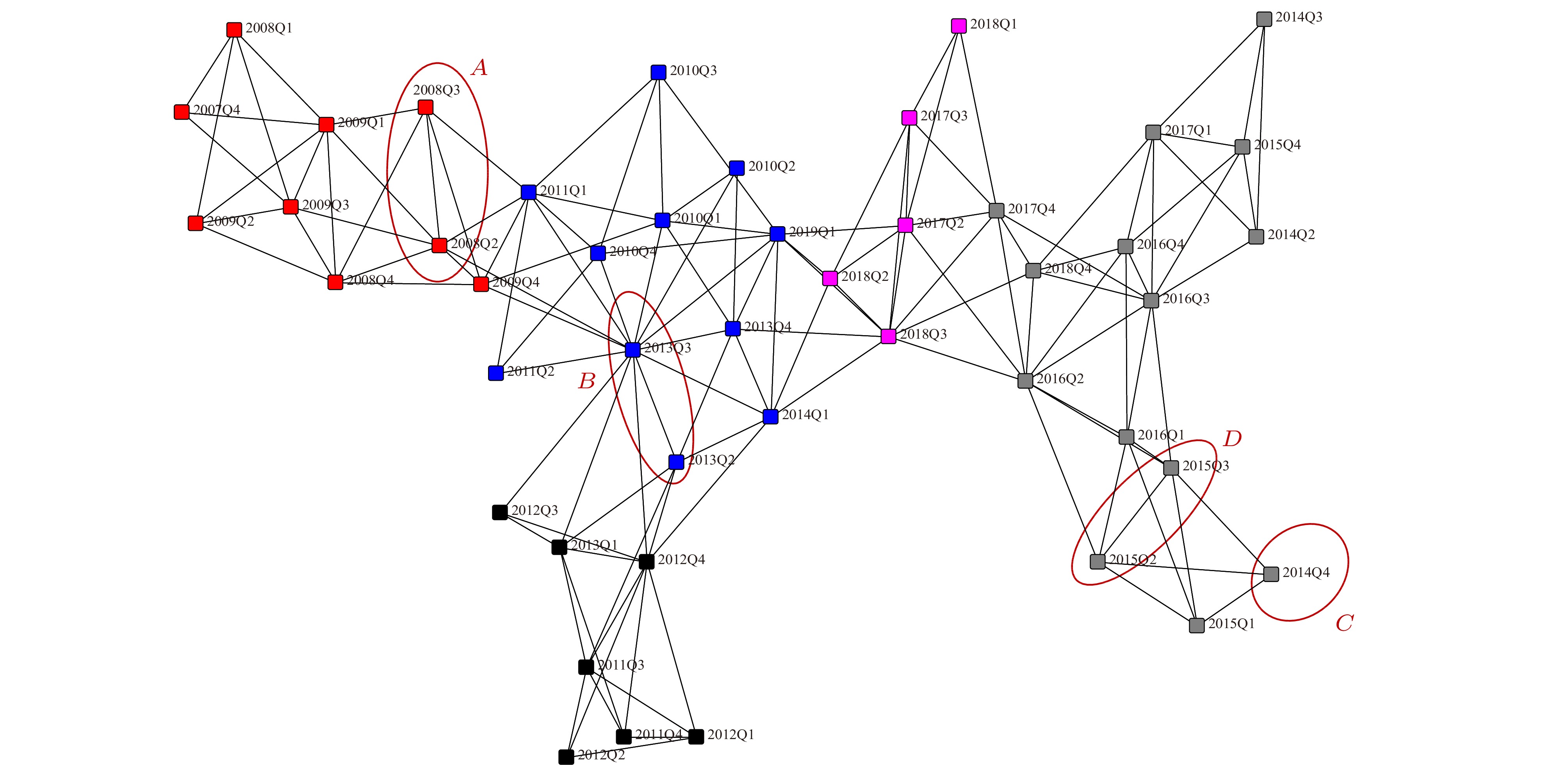
-
Aiming at the state transition between bank networks, we propose a time-varying state network model. In this model, we classify the bank networks in each time period by the kmeans method, and use directed minimum spanning tree(DMST) method to describe the topological structure of each kind of bank network. We also construct a time-varying bank state network by the planar maximally filtered graph(PMFG) method. The state network can be used to find the source of bank risk and conduct the time-varying analysis. We put into the model the inter-bank lending data of 15 listed Chinese commercial banks from the fourth quarter of 2007 to the first quarter of 2019. The results show that the short-term continuity jump between the bank states can effectively describe the occurrence of financial crisis. For example, before and after the global financial crisis in 2008, there was a short-term jump between two states. From the “money shortage” in 2013 to the stock market crash in 2015, there were four short-term jumps between states. At the same time, the outgoing degree of each directed bank state network is directly proportional to the contagion effect, and the incoming degree is inversely proportional to the steady degree of the risk faced by the bank. The sequential bank state network has the memory characteristic, which can provide the central bank for decision basis to prevent the systematic risk.
-
Keywords:
- bank network /
- directed minimum spanning tree /
- risk contagion intensity /
- planar maximally filtered graph
[1] Anand K, Lelyveld I, Banai Á, Friedrich S, Garratt R, Hałaj G, Fique J, Hansen I, Jaramillo S M, Lee H, Molina J L, Nobili S, Rajan S, Salakhova D, Silva T C, Silvestri L, Souza S 2018 J. Financ. Stabil. 35 107
Google Scholar
[2] 唐文进, 苏帆 2017 经济研究 04 19
Tang W J, Su F 2017 ERJ 04 19
[3] Müller J 2006 J. Financ. Serv. Res. 29 37
Google Scholar
[4] Wells S 2004 B.E.Q. Bull. 3 331
[5] Upper C, Worms A 2004 Eur. Econ. Rev. 48 827
Google Scholar
[6] Anand K, Craig B, Peter G 2015 Quant. Financ. 15 625
Google Scholar
[7] 李守伟, 何建敏, 庄亚明 2010 系统工程 5 20
Li S W, He J M, Zhuang Y M 2010 Syst. Eng. 5 20
[8] 范宏, 郑阳, 杨明明 2019 系统工程 37 101
Fan H, Zheng Y, Yang M M 2019 Syst. Eng. 37 101
[9] 王明亮, 何建敏, 李守伟 2013 中国管理科学 S1 237
Wang M L, He J M, Li S W 2013 Chin. J. Manage. Sci. S1 237
[10] Zhou L, Qiu L, Gu C G, Yang H J 2018 EPL 121 48002
Google Scholar
[11] 邓向荣, 曹红 2016 中央财经大学学报 3 52
Deng X R, Cao H 2016 J. Central Univ. Financ. Econ. 3 52
[12] 胡利琴, 胡蝶, 彭红枫 2018 国际金融研究 06 53
Google Scholar
Hu L Q, Hu D, Peng H F 2018 Stud. Inter. Fin. 06 53
Google Scholar
[13] Constantin A, Peltonen T A, Sarlin P 2018 J. Financ. Stabil. 35 226
Google Scholar
[14] 陈梦根, 赵雨涵 2019 经济研究 54 49
Chen M G, Zhao Y H 2019 Econ. Res. J. 54 49
[15] 李智, 牛晓健 2018 大连理工大学学报(社会科学版) 2 19
Li Z, Niu X J 2018 J. Dalian Univ. Technol. (Soc. Sci.) 2 19
[16] 李政, 刘淇, 梁琪 2019 统计研究 36 23
Li Z, Liu Q, Liang Q 2019 Stat. Res. 36 23
[17] Garratt R, Mahadeva L, Svirydzenka K 2012 SSRN Electron. J. 413 1
[18] Spelta A and Araújo T 2012 Physica A 391 5572
Google Scholar
[19] Zhang J, Small M 2006 Phys. Rev. Lett. 96 238701
Google Scholar
[20] Xu X K, Zhang J, Small M 2008 PNAS 105 19601
Google Scholar
[21] Münnix M C, Shimada T, Schäfer R, Leyvraz F, Seligman T H, Guhr T, Stanley H E 2012 Sci. Rep. 2 644
Google Scholar
[22] Qiu L, Gu C G, Xiao Q, Yang H J, Wu G L 2018 Physica A 492 1120
Google Scholar
[23] Tumminello M, Aste T, Di Matteo T, Mantegna R N 2005 PNAS 102 10421
Google Scholar
[24] Holme P, Saramäki J 2012 Phys. Rep. 519 97
Google Scholar
[25] Blien U, Graef F 1998 Entropy Optimizing Methods for the Estimation of Tables (Germany: Springer) p3
[26] Wilks D S 2004 Mon. Weather. Rev. 132 1329
Google Scholar
[27] Kwon O, Yang J S 2008 EPL 82 680031
[28] Girvan M, Newman M E J 2002 PNAS 99 7821
Google Scholar
[29] 蒋海, 张锦意 2018 财贸经济 39 50
Jiang H, Zhang J Y 2018 Financ. Trad. Econ. 39 50
-
图 1 主体方法和流程图
Figure 1. Main method and flow chart.
图 2 距离比率与比率变化率
Figure 2. Distance ratio and rate of change.
图 3 银行拆借矩阵状态演化图
Figure 3. State evolution of bank lending matrix.
图 4 8类银行状态矩阵图
Figure 4. Bank matrix diagram of 8 states.
图 5 各个银行状态之间的相关矩阵
Figure 5. Correlation matrix between Bank states.
图 6 状态1—4的有向最小生成树 (a) 状态1的有向生成树; (b) 状态2的有向生成树; (c) 状态3的有向生成树; (d) 状态4的有向生成树
Figure 6. . Directed network diagram of state 1 to 4: (a) Directed network diagram of state 1 (b) directed network diagram of state 2; (c) directed network diagram of state 3; (d) directed network diagram of state 4.
图 7 状态5—8的有向最小生成树 (a) 状态5的有向生成树; (b) 状态6的有向生成树; (c) 状态7的有向生成树; (d) 状态8的有向生成树
Figure 7. Directed network diagram of state 5 to 8: (a) Directed network diagram of state 5; (b) directed network diagram of state 6; (c) directed network diagram of state 7; (d) directed network diagram of state 8.
图 8 各个时间状态下拆借矩阵关系
Figure 8. Lending matrix relationship in different time states.
表 1 商业银行汇总
Table 1. Summary of commercial banks.
编号 银行 类型 编号 银行 类型 1 浦发银行 股份制商业银行 2 民生银行 股份制商业银行 3 华夏银行 股份制商业银行 4 招商银行 股份制商业银行 5 兴业银行 股份制商业银行 6 北京银行 地方商业银行 7 上海银行 地方商业银行 8 中国农业银行 国有商业银行 9 中国交通银行 国有商业银行 10 中国工商银行 国有商业银行 11 中国建设银行 国有商业银行 12 中国银行 国有商业银行 13 中信银行 股份制商业银行 14 平安银行 股份制商业银行 15 宁波银行 地方商业银行 
DownLoad: CSV
表 2 8个状态矩阵的相关矩阵
Table 2. Correlation matrix of eight state matrices.
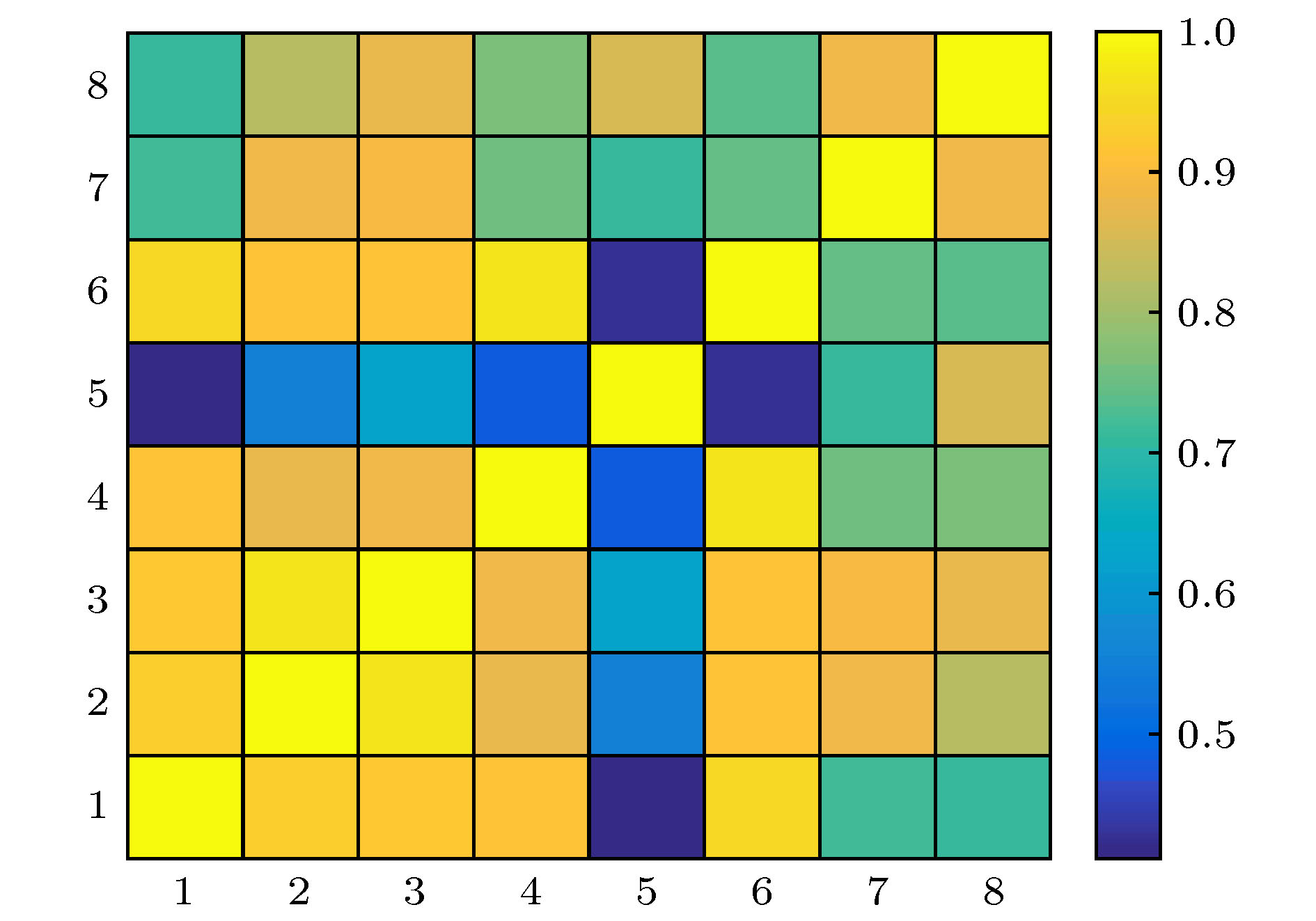
状态1 状态2 状态3 状态4 状态5 状态6 状态7 状态8 状态1 1.000 0.927 0.918 0.909 0.410 0.949 0.714 0.708 状态2 0.927 1.000 0.968 0.874 0.549 0.911 0.881 0.819 状态3 0.918 0.968 1.000 0.887 0.630 0.911 0.893 0.875 状态4 0.909 0.874 0.887 1.000 0.481 0.963 0.757 0.767 状态5 0.410 0.549 0.63 0.481 1.000 0.422 0.707 0.861 状态6 0.949 0.911 0.911 0.963 0.422 1.000 0.75 0.734 状态7 0.714 0.881 0.893 0.757 0.707 0.750 1.000 0.884 状态8 0.708 0.819 0.875 0.767 0.861 0.734 0.884 1.000
DownLoad: CSV
表 3 8个状态矩阵的全局相似度
Table 3. Global similarity of eight state matrices.
状态 1 2 3 4 5 6 7 8 全局相似度 6.536 6.929 7.082 6.638 5.060 6.639 6.587 6.647
DownLoad: CSV
表 4 银行状态网络拓扑特性统计
Table 4. Statistics of topological characteristics of banking state network.
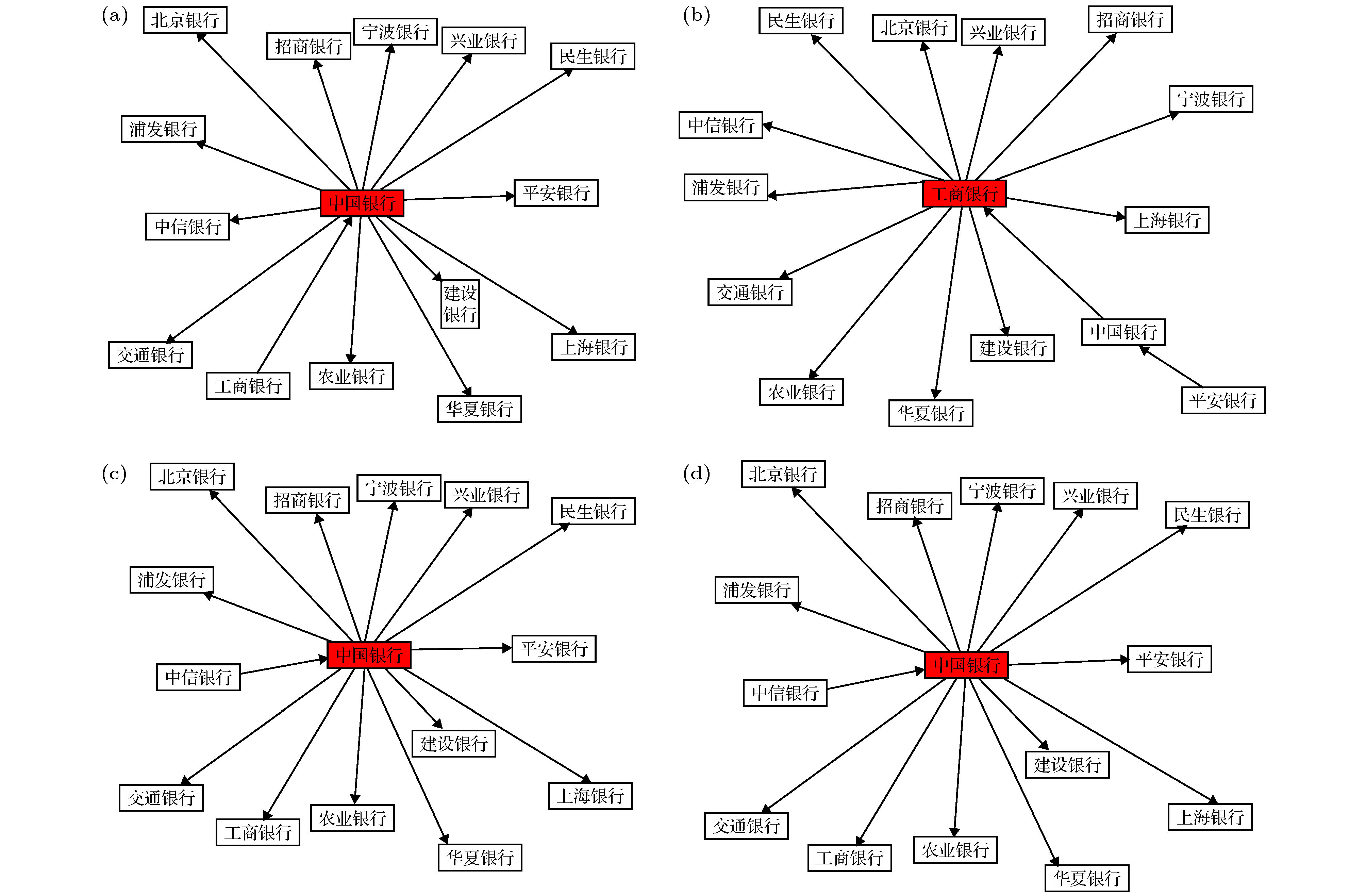
银行 状态1出度 状态2出度 状态3出度 状态4出度 状态5出度 状态6出度 状态7出度 状态8出度 头节点数 中心节点数 浦发 0 0 0 0 0 0 0 0 0 0 民生 1 1 1 0 0 0 0 0 3 0 华夏 0 0 0 0 0 0 0 0 0 0 招商 0 0 0 0 0 0 0 0 0 0 兴业 0 0 0 0 0 0 0 0 0 0 北京 0 0 0 0 0 0 0 0 0 0 上海 0 0 0 0 0 0 0 0 0 0 农业 0 5 1 0 0 0 0 0 0 1 交通 0 0 0 1 0 0 0 0 0 0 工商 13 0 5 11 1 12 0 0 1 4 建设 0 0 0 0 0 0 0 0 0 0 中国 0 8 7 1 13 1 13 13 0 5 中信 0 0 0 1 0 0 1 1 3 0 平安 0 0 0 0 0 1 0 0 1 0 宁波 0 0 0 0 0 0 0 0 0 0
DownLoad: CSV
-
[1] Anand K, Lelyveld I, Banai Á, Friedrich S, Garratt R, Hałaj G, Fique J, Hansen I, Jaramillo S M, Lee H, Molina J L, Nobili S, Rajan S, Salakhova D, Silva T C, Silvestri L, Souza S 2018 J. Financ. Stabil. 35 107
Google Scholar
[2] 唐文进, 苏帆 2017 经济研究 04 19
Tang W J, Su F 2017 ERJ 04 19
[3] Müller J 2006 J. Financ. Serv. Res. 29 37
Google Scholar
[4] Wells S 2004 B.E.Q. Bull. 3 331
[5] Upper C, Worms A 2004 Eur. Econ. Rev. 48 827
Google Scholar
[6] Anand K, Craig B, Peter G 2015 Quant. Financ. 15 625
Google Scholar
[7] 李守伟, 何建敏, 庄亚明 2010 系统工程 5 20
Li S W, He J M, Zhuang Y M 2010 Syst. Eng. 5 20
[8] 范宏, 郑阳, 杨明明 2019 系统工程 37 101
Fan H, Zheng Y, Yang M M 2019 Syst. Eng. 37 101
[9] 王明亮, 何建敏, 李守伟 2013 中国管理科学 S1 237
Wang M L, He J M, Li S W 2013 Chin. J. Manage. Sci. S1 237
[10] Zhou L, Qiu L, Gu C G, Yang H J 2018 EPL 121 48002
Google Scholar
[11] 邓向荣, 曹红 2016 中央财经大学学报 3 52
Deng X R, Cao H 2016 J. Central Univ. Financ. Econ. 3 52
[12] 胡利琴, 胡蝶, 彭红枫 2018 国际金融研究 06 53
Google Scholar
Hu L Q, Hu D, Peng H F 2018 Stud. Inter. Fin. 06 53
Google Scholar
[13] Constantin A, Peltonen T A, Sarlin P 2018 J. Financ. Stabil. 35 226
Google Scholar
[14] 陈梦根, 赵雨涵 2019 经济研究 54 49
Chen M G, Zhao Y H 2019 Econ. Res. J. 54 49
[15] 李智, 牛晓健 2018 大连理工大学学报(社会科学版) 2 19
Li Z, Niu X J 2018 J. Dalian Univ. Technol. (Soc. Sci.) 2 19
[16] 李政, 刘淇, 梁琪 2019 统计研究 36 23
Li Z, Liu Q, Liang Q 2019 Stat. Res. 36 23
[17] Garratt R, Mahadeva L, Svirydzenka K 2012 SSRN Electron. J. 413 1
[18] Spelta A and Araújo T 2012 Physica A 391 5572
Google Scholar
[19] Zhang J, Small M 2006 Phys. Rev. Lett. 96 238701
Google Scholar
[20] Xu X K, Zhang J, Small M 2008 PNAS 105 19601
Google Scholar
[21] Münnix M C, Shimada T, Schäfer R, Leyvraz F, Seligman T H, Guhr T, Stanley H E 2012 Sci. Rep. 2 644
Google Scholar
[22] Qiu L, Gu C G, Xiao Q, Yang H J, Wu G L 2018 Physica A 492 1120
Google Scholar
[23] Tumminello M, Aste T, Di Matteo T, Mantegna R N 2005 PNAS 102 10421
Google Scholar
[24] Holme P, Saramäki J 2012 Phys. Rep. 519 97
Google Scholar
[25] Blien U, Graef F 1998 Entropy Optimizing Methods for the Estimation of Tables (Germany: Springer) p3
[26] Wilks D S 2004 Mon. Weather. Rev. 132 1329
Google Scholar
[27] Kwon O, Yang J S 2008 EPL 82 680031
[28] Girvan M, Newman M E J 2002 PNAS 99 7821
Google Scholar
[29] 蒋海, 张锦意 2018 财贸经济 39 50
Jiang H, Zhang J Y 2018 Financ. Trad. Econ. 39 50
DownLoad:
Catalog
Metrics
- Abstract views: 6454
- PDF Downloads: 85
- Cited By: 0
