新型压缩感知计算模型分析三维电大目标电磁散射特性

王攀; 王仲根; 孙玉发; 聂文艳

doi:10.7498/aps.72.20221532

摘要

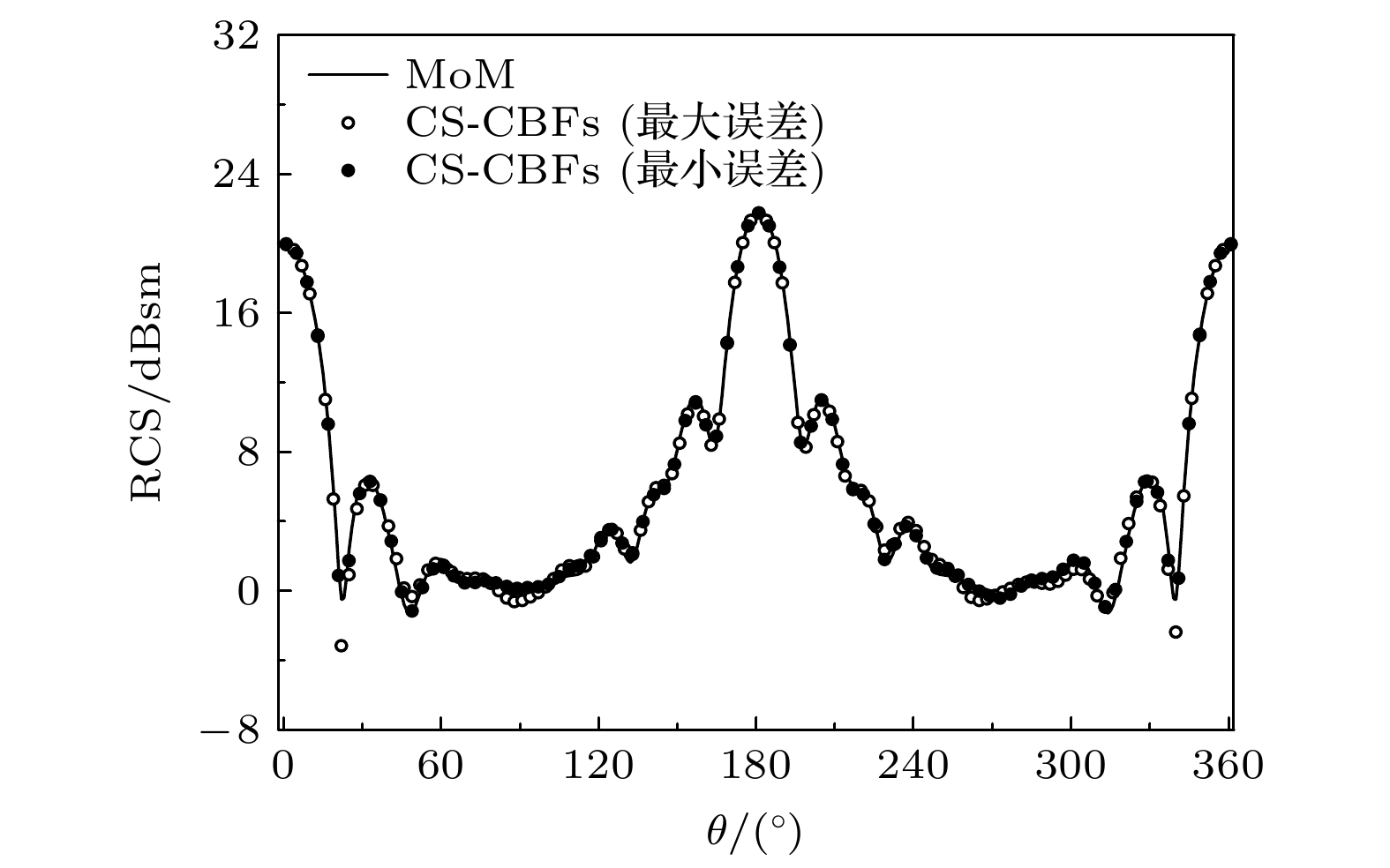
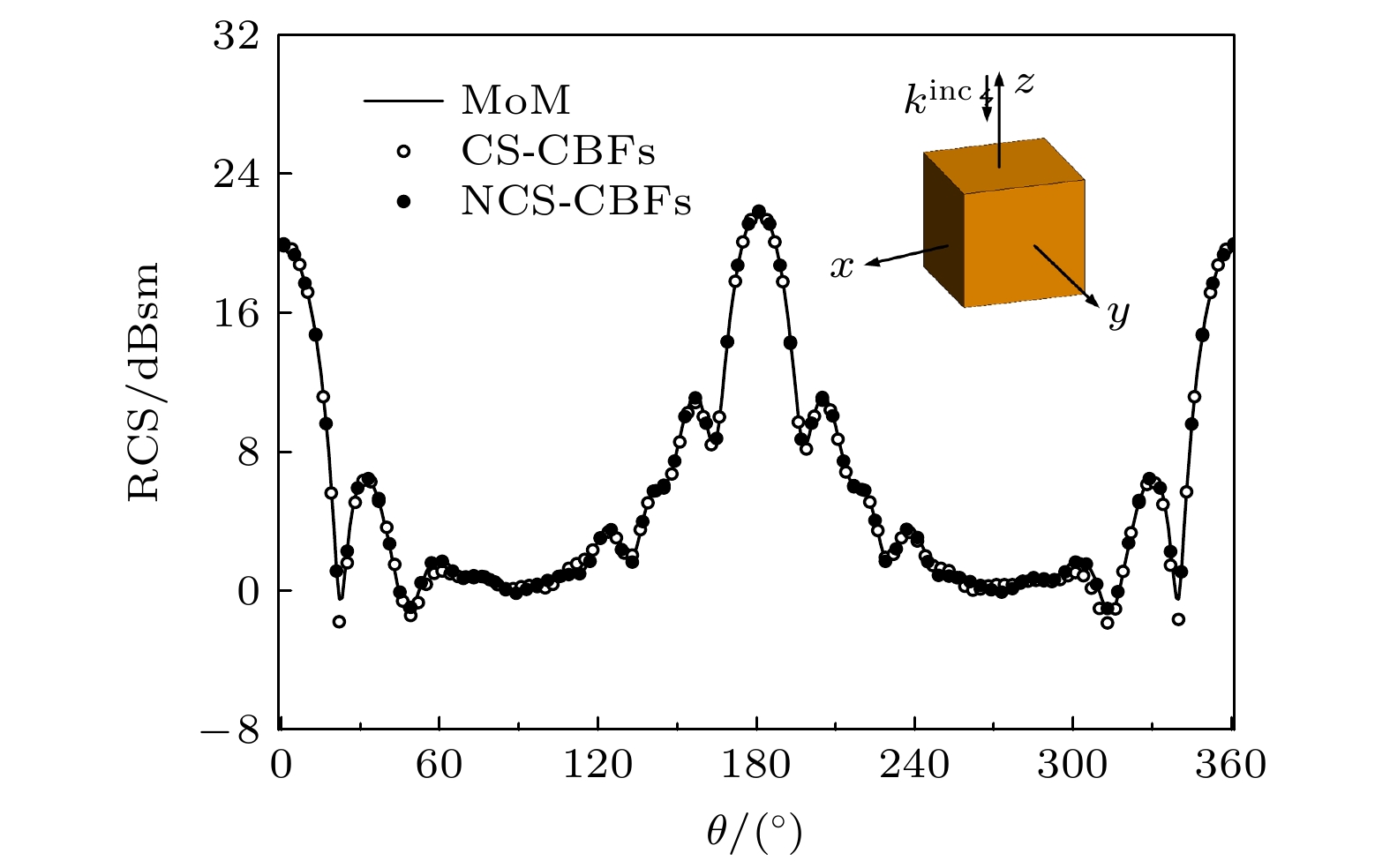
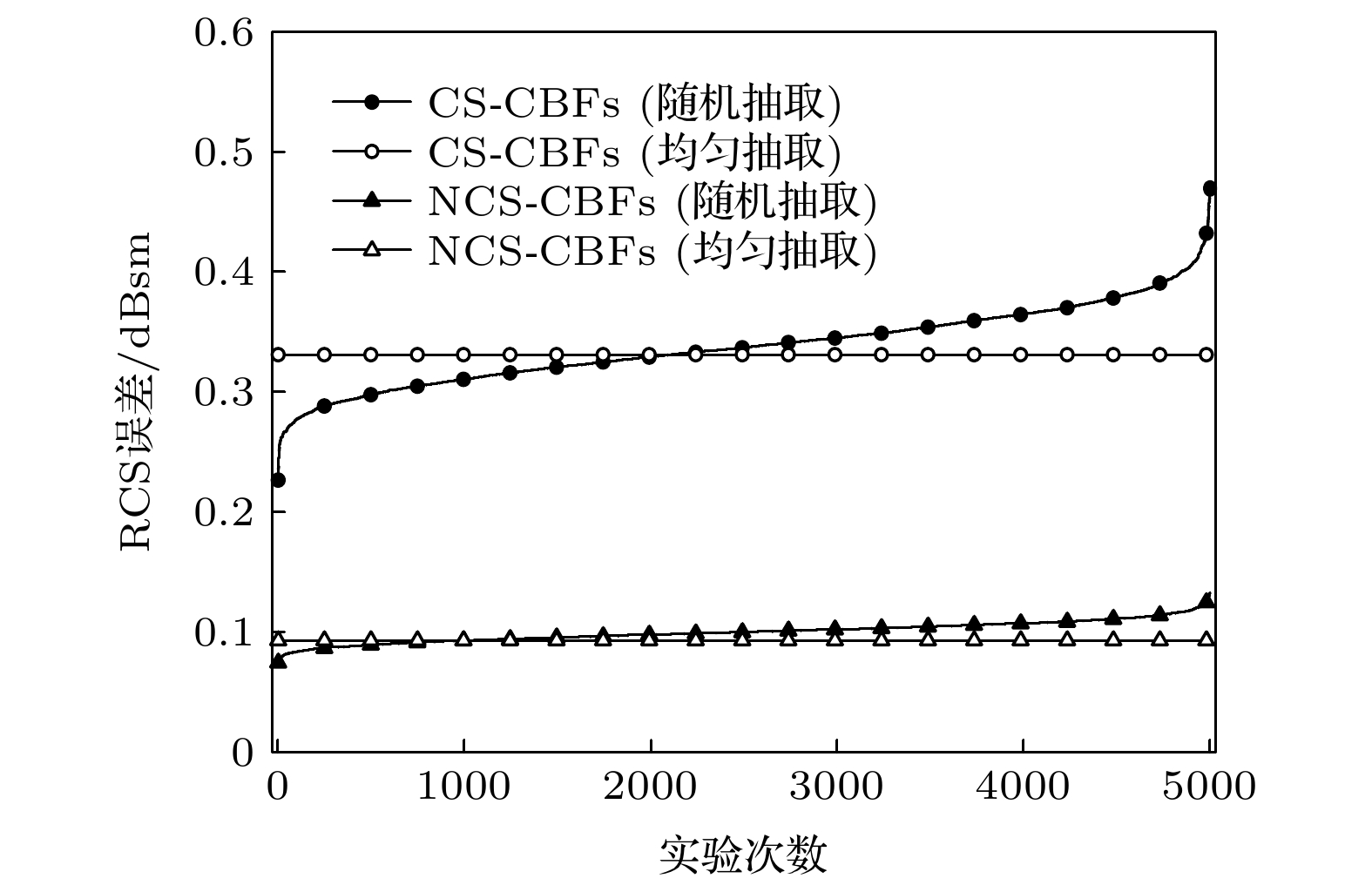
为提高基于压缩感知技术的矩量法在三维电大目标双站电磁散射问题中的计算效率和稳定性, 提出新的稀疏、测量和重构方法, 构建一种新型压缩感知计算模型. 不同于基于欠定方程的传统的压缩感知计算模型, 新型计算模型首先采用按行均匀抽取阻抗矩阵的方法构造测量矩阵以获得稳定的计算结果; 然后, 基于Foldy-Lax方程生成多阶特征基函数并作为稀疏基对感应电流进行稀疏转换; 再依据少数低阶特征基函数足以近似表征感应电流的先验条件, 将恢复算法简化为最小二乘法; 最后, 将矩阵方程转换为一个超定系统并采用最小二乘法解出电流系数. 与传统的计算模型相比, 新型计算模型不仅可以获得更加稳定的精确解, 还可以显著提高电大目标双站散射问题的求解效率和计算精度. 数值仿真结果证明了新方法的可行性和高效性.

关键词:

Abstract

The method of moments is one of the most effective algorithms for solving electromagnetic scattering problems. However, the high computational complexity limits its application to electrically large problems. As an improved algorithm, the compressive sensing-based method of moments introduces the compressive sensing technique into the algorithmic structure, which avoids the inverse of the matrix equation and improves the computational efficiency. Using the underdetermined equation-based calculation model, this scheme is utilized to efficiently analyze the bistatic scattering of the objects. In this technique, the extracted few rows from the impedance matrix are used to construct the measurement matrix. Nevertheless, the results are unstable due to the random extraction utilized to build the measurement matrix. Furthermore, it is challenging task to provide an appropriate sparse basis for the induced currents of three-dimensional objects discretized by the Rao-Wilton-Glisson basis functions. To address the aforementioned issues, a novel compressive sensing calculation model that enhances measurement matrix building, sparse basis construction, and recovery is provided in this paper. First, several rows of the impedance matrix are uniformly extracted to produce consistent computation results, which is opposed to the randomly constructed measurement matrix in the conventional technique. The number of rows to be extracted is typically set to be 3–5 times the number of basis functions for high accuracy. Then, the characteristic basis functions based on the Foldy-Lax equation are employed to construct the sparse basis. Considering the prior knowledge that the lower order characteristic basis functions are dominant, the columns of the recovery matrix corresponding to some low-order characteristic functions are determined in advance as the columns that will be identified by the recovery algorithm, thus simplifying the recovery algorithm to a least-squares operation. Obviously, the matrix equation is reduced to an overdetermined equation instead of the underdetermined equation since only a few low-order basis functions are to be computed. Compared with the conventional compressive sensing-based method of moments with characteristic basis functions, the computation time is significantly reduced in terms of constructing the basis functions and recovering the current coefficients, while the accuracy is improved. Finally, both the suggested method and the conventional compressive sensing-based method of moments are used to simulate the bistatic radar cross sections of the perfect electrical conductor cube, cylinder, and missile model. The efficiency and accuracy of the proposed method are verified by the numerical results.

Keywords:

作者及机构信息

1.
安徽理工大学电气与信息工程学院, 淮南　232001

2.
安徽大学电子信息工程学院, 合肥　230601

3.
淮南师范学院机械与电气工程学院, 淮南　232001

通信作者: 王仲根, zgwang@ahu.edu.cn

基金项目: 国家自然科学基金(批准号: 62071004)、安徽省自然科学基金(批准号: 2108085MF200)和安徽高校自然科学重点项目(批准号: KJ2020A0307)资助的课题.

Authors and contacts

1.
School of Electrical and Information Engineering, Anhui University of Science and Technology, Huainan 232001, China

2.
School of Electronics and Information Engineering, Anhui University, Hefei 230601, China

3.
School of Mechanical and Electrical Engineering, Huainan Normal University, Huainan 232001, China

Corresponding author: Wang Zhong-Gen, zgwang@ahu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 62071004), the Natural Science Foundation of Anhui Provincial, China (Grant No. 2108085MF200), and the Natural Science Foundation of the Anhui Higher Education Institutions of China (Grant No. KJ2020A0307).

文章全文 : translate this paragraph

参考文献

[1]	Hanington R F 1968 Field Computation by Moment Methods (New York: Maxillan) p6
[2]	Song J M, Lu C C, Chew W C 1997 IEEE Trans. Antenn. Propag. 45 1488 Google Scholar
[3]	Freni A, Vita D P, Pirinoli P, Matekovits L, Vecchi G 2011 IEEE Trans. Antenn. Propag. 59 4588 Google Scholar
[4]	Jrgensen E, Volakis J L, Meincke P, Breinbjerg O 2004 IEEE Trans. Antennas Propag. 52 2985 Google Scholar
[5]	Prakash V V S, Mittra R 2003 Microw. Opt. Technol. Lett. 36 95 Google Scholar
[6]	Sun Y F, Chan C H, Mittra R 2003 IEEE Antennas and Propagation Society International Symposium Columbus, June 22–27, 2003 p1068
[7]	Donoho D L 2006 IEEE Trans. Inform. Theory 52 1289 Google Scholar
[8]	Chen M S, Liu F L, Du H M, Wu X L 2011 IEEE Antennas Wirel. Propag. Lett. 10 1243 Google Scholar
[9]	柴水荣, 郭立新 2015 64 060301 Google Scholar Chai S R, Guo L X 2015 Acta Phys. Sin. 64 060301 Google Scholar
[10]	Chai S R, Guo L X 2016 IEEE Trans. Antennas Propag. 64 3545 Google Scholar
[11]	Liu Y, Qi Q, Cao X Y, Chen M S, Deng G Q, Huang Z X, WU X L 2021 Int. J. Antennas Propag. 2021 9912502 Google Scholar
[12]	Kong M, Chen M S, Cao X Y, Zhang L, Qi Q, Wu X L 2020 IEEE Access 8 127640 Google Scholar
[13]	Kong M, Chen M S, Cao X Y, Zhu J B, Kuang X J, Qi Q, Wu X L 2021 IEEE Antennas Wirel. Propag. Lett. 20 1527 Google Scholar
[14]	王哲, 王秉中 2014 63 120202 Google Scholar Wang Z, Wang B Z 2014 Acta Phys. Sin. 63 120202 Google Scholar
[15]	Chai S R, Guo L X 2016 IEEE Antennas Wirel. Propag. Lett. 15 1771 Google Scholar
[16]	Wang Z, Wang B Z, Shao W 2015 J. Electromagn. Waves Appl. 29 683 Google Scholar
[17]	Chai S R, Guo L X 2016 J. Electromagn. Waves Appl. 30 1755 Google Scholar
[18]	Cao X Y, Chen M S, Qi Q, Kong M, Hu J H, Zhang L, Wu X L 2020 IEEE Microw. Wireless Compon. Lett. 30 541 Google Scholar
[19]	丁亚辉, 孙玉发, 朱金玉 2018 67 100201 Google Scholar Ding Y H, Sun Y F, Zhu J Y 2018 Acta Phys. Sin. 67 100201 Google Scholar
[20]	Wang Z G, Wang P, Sun Y F, Nie W Y 2022 IEEE Antennas Wirel. Propag. Lett. 21 1817 Google Scholar
[21]	Candès E J 2008 Comptes Rendus Mathematique 346 589 Google Scholar
[22]	Wang J, Kwon S, Shim B 2012 IEEE Trans. Signal Process. 60 6202 Google Scholar

施引文献

图 1 5000次实验的RCS误差分布

Fig. 1. RCS error distribution of 5000 experiments.

下载: 全尺寸图片幻灯片

图 2 随机抽取方法下CS-CBFs的不同计算结果对比 (φ = 0°)

Fig. 2. Comparison of different calculation results of CS-CBFs with randomly extracting (φ = 0°).

下载: 全尺寸图片幻灯片

图 3 不同抽取行数下两种方法的RCS误差和求解时间

Fig. 3. RCS error and solution time of two methods with different number of extracted rows.

下载: 全尺寸图片幻灯片

图 4 不同基函数阶数下本文方法的RCS误差和求解时间

Fig. 4. RCS error and solution time of the proposed method for different orders of basis functions.

下载: 全尺寸图片幻灯片

图 5 立方体水平极化双站RCS (φ = 0°)

Fig. 5. Bistatic RCS of cube in horizontal polarization　(φ = 0°).

下载: 全尺寸图片幻灯片

图 6 圆柱体垂直极化双站RCS (φ = 0°)

Fig. 6. Bistatic RCS of cylinder in vertical polarization (φ = 0°).

下载: 全尺寸图片幻灯片

图 7 导弹水平极化双站RCS (φ = 0°)

Fig. 7. Bistatic RCS of missile in horizontal polarization (φ = 0°).

下载: 全尺寸图片幻灯片

表 1 测量矩阵与稀疏基之间的相关系数

Table 1. Correlation coefficient of the measurement matrix and sparse basis.

方法	CS-CBFs		NCS-CBFs
方法	均匀抽取	随机抽取	均匀抽取	随机抽取
相关系数	0.033 + 0.132i	0.100 + 0.021i	–0.040 + 0.087i	0.047 + 0.053i

下载: 导出CSV

表 2 计算时间和RCS误差比较

Table 2. Comparison of computation time and RCS error.

目标	方法	构造基函数时间/s	重构电流系数时间/s	总求解时间/s	RCS 误差/dBsm
导体立方体	CS-CBFs	43.8	3.9	48.0	0.33
导体立方体	NCS-CBFs	24.0	1.3	25.6	0.09
导体圆柱	CS-CBFs	287.2	60.0	348.1	1.48
导体圆柱	NCS-CBFs	200.4	6.7	208.0	0.71
导弹	CS-CBFs	75.4	2.4	78.1	1.02
导弹	NCS-CBFs	23.5	0.8	24.7	0.28

下载: 导出CSV

map

[1]	Hanington R F 1968 Field Computation by Moment Methods (New York: Maxillan) p6
[2]	Song J M, Lu C C, Chew W C 1997 IEEE Trans. Antenn. Propag. 45 1488 Google Scholar
[3]	Freni A, Vita D P, Pirinoli P, Matekovits L, Vecchi G 2011 IEEE Trans. Antenn. Propag. 59 4588 Google Scholar
[4]	Jrgensen E, Volakis J L, Meincke P, Breinbjerg O 2004 IEEE Trans. Antennas Propag. 52 2985 Google Scholar
[5]	Prakash V V S, Mittra R 2003 Microw. Opt. Technol. Lett. 36 95 Google Scholar
[6]	Sun Y F, Chan C H, Mittra R 2003 IEEE Antennas and Propagation Society International Symposium Columbus, June 22–27, 2003 p1068
[7]	Donoho D L 2006 IEEE Trans. Inform. Theory 52 1289 Google Scholar
[8]	Chen M S, Liu F L, Du H M, Wu X L 2011 IEEE Antennas Wirel. Propag. Lett. 10 1243 Google Scholar
[9]	柴水荣, 郭立新 2015 64 060301 Google Scholar Chai S R, Guo L X 2015 Acta Phys. Sin. 64 060301 Google Scholar
[10]	Chai S R, Guo L X 2016 IEEE Trans. Antennas Propag. 64 3545 Google Scholar
[11]	Liu Y, Qi Q, Cao X Y, Chen M S, Deng G Q, Huang Z X, WU X L 2021 Int. J. Antennas Propag. 2021 9912502 Google Scholar
[12]	Kong M, Chen M S, Cao X Y, Zhang L, Qi Q, Wu X L 2020 IEEE Access 8 127640 Google Scholar
[13]	Kong M, Chen M S, Cao X Y, Zhu J B, Kuang X J, Qi Q, Wu X L 2021 IEEE Antennas Wirel. Propag. Lett. 20 1527 Google Scholar
[14]	王哲, 王秉中 2014 63 120202 Google Scholar Wang Z, Wang B Z 2014 Acta Phys. Sin. 63 120202 Google Scholar
[15]	Chai S R, Guo L X 2016 IEEE Antennas Wirel. Propag. Lett. 15 1771 Google Scholar
[16]	Wang Z, Wang B Z, Shao W 2015 J. Electromagn. Waves Appl. 29 683 Google Scholar
[17]	Chai S R, Guo L X 2016 J. Electromagn. Waves Appl. 30 1755 Google Scholar
[18]	Cao X Y, Chen M S, Qi Q, Kong M, Hu J H, Zhang L, Wu X L 2020 IEEE Microw. Wireless Compon. Lett. 30 541 Google Scholar
[19]	丁亚辉, 孙玉发, 朱金玉 2018 67 100201 Google Scholar Ding Y H, Sun Y F, Zhu J Y 2018 Acta Phys. Sin. 67 100201 Google Scholar
[20]	Wang Z G, Wang P, Sun Y F, Nie W Y 2022 IEEE Antennas Wirel. Propag. Lett. 21 1817 Google Scholar
[21]	Candès E J 2008 Comptes Rendus Mathematique 346 589 Google Scholar
[22]	Wang J, Kwon S, Shim B 2012 IEEE Trans. Signal Process. 60 6202 Google Scholar

计量

文章访问数: 4115
PDF下载量: 80
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板