-
In this review, we give a brief review on the recent progress in the theoretical research of quench dynamics in topological band systems. Beginning with two band models, we introduce conception of dynamical Chern number and give the connection between the dynamical Chern number and topological invariant in the corresponding equilibrium systems. Then by studying the 1 + 1 dimensional parent Hamiltonian, we show the complete dynamical classification of Altland-Zirnbauer classes, and show the crossing of entanglement spectrum as a feature of dynamical bulk edge correspondence. Furthermore, we consider the impact of the disorder and band dispersion. At last, we show the experimental simulation of dynamical Chern number by a superconducting qubit system.
-
Keywords:
- topological phase transition /
- quench dynamics
[1] Klitzing K V, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Thouless D J, Kohmoto M, Nightingale M P, Nijs M den Nijs 1982 Phys. Rev. Lett. 49 405
Google Scholar
[3] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[4] Qi X, Zhang S 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[5] Chiu C, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005
Google Scholar
[6] Atala M, Aidelsburger M, Barreiro J T, Abanin D, Kitagawa T, Demler E, Bloch I 2013 Nat. Phys. 9 795
Google Scholar
[7] Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, Esslinger T 2014 Nature (London)
515 237 Google Scholar
[8] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y, Chen S, Liu X J, Pan J W 2016 Science 354 83
Google Scholar
[9] Aidelsburger M, Atala M, Lohse M, Barreiro J T, Paredes B, Bloch I 2013 Phys. Rev. Lett. 111 185301
Google Scholar
[10] Aidelsburger M, Lohse M, Schweizer C, Atala M, Barreiro J T, Nascimbne S, Cooper N R, Bloch I, Goldman N 2015 Nat. Phys. 11 162
Google Scholar
[11] Miyake H, Siviloglou G A, Kennedy C J, Burton W C, Ketterle W 2013 Phys. Rev. Lett. 111 185302
Google Scholar
[12] Caio M D, Cooper N R, Bhaseen M J 2015 Phys. Rev. Lett. 115 236403
Google Scholar
[13] Alessio L D, Rigol M 2015 Nat. Commun. 6 8336
Google Scholar
[14] Hu Y, Zoller P, Budich J C 2016 Phys. Rev. Lett. 117 126083
[15] Wilson J H, Song J C W, Refael G 2016 Phys. Rev. Lett. 117 235032
[16] McGinley M, Cooper N R 2018 Phys. Rev. Lett. 121 090401
Google Scholar
[17] McGinley M, Cooper N R 2019 Phys. Rev. B 99 075418
Google Scholar
[18] Wang C, Zhang P, Chen X, Yu J, Zhai H 2017 Phys. Rev. Lett. 118 185701
Google Scholar
[19] Chen X, Wang C, Yu J 2019 arXiv: 1907.08840
[20] Tarnowski M, Unal F N, Flaschner N, Rem B S, Eckardt A, Sengstock K, Weitenberg C 2019 Nat. Commun. 10 1728
Google Scholar
[21] Yang C, Li L, Chen S 2018 Phys. Rev. B(R)
97 060304 Google Scholar
[22] Guo X Y, Yang C, Zeng Y, Peng Y, Li H K, Deng H, Jin Y R, Chen S, Zheng D N, Fan H 2019 Phys. Rev. Applied 11 044080
Google Scholar
[23] Gong Z, Ueda M 2018 Phys. Rev. Lett. 121 250601
Google Scholar
[24] Zhang L, Zhang L, Niu S, Liu X J 2018 Science Bulletin 63 1385
Google Scholar
[25] Zhang L, Zhang L, Liu X J 2019 Phys. Rev. A 99 053606
Google Scholar
[26] Zhang L, Zhang L, Liu X J 2019 arXiv: 1907.08840
[27] Sun W, Yi C R, Wang B Z, Zhang W W, Sanders B C, Xu X T, Wang Z Y, Schmiedmayer J, Deng Y J, Liu X J, Chen S, Pan J W 2019 Phys. Rev. Lett. 121 250403
[28] Lieb E H, Robinson D W 1972 Commun. Math. Phys. 28 251
Google Scholar
[29] Gong Z, Kura N, Sato M, Ueda M 2019 arXiv: 1904.12464
[30] Altland A, Zirnbauer M R 1997 Phys. Rev. B 55 1142
Google Scholar
[31] Schnyder A P, Ryu S, Furusaki A, Ludwig A W W 2008 Phys. Rev. B 78 2208
[32] Kitaev A 2009 AIP Conf. Proc. 22 1134
[33] Kitaev A 2001 Ann. Phys. (NY)
303 2 [34] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[35] Li L, Yang C, Chen S 2016 Eur. Phys. J. B 89 195
Google Scholar
[36] Teo J C Y, Kane C L 2010 Phys. Rev. B 82 115120
Google Scholar
[37] Shiozaki K, Sato M 2014 Phys. Rev. B 90 165114
Google Scholar
[38] Chiu C K, Yao H, Ryu S 2013 Phys. Rev. B 88 075142
Google Scholar
[39] Fu L, Kane C 2006 Phys. Rev. B 74 195312
Google Scholar
[40] Moore J E, Balents L 2007 Phys. Rev. B(R)
75 121306 Google Scholar
[41] Wen X G 1992 Int. J. Mod. Phys. B 06 1711
Google Scholar
[42] Fidkowski L 2010 Phys. Rev. Lett. 104 130502
Google Scholar
[43] Peschel I 2002 J. Phys. A 36 L205
[44] Hughes T L, Prodan E, Bernevig B A 2011 Phys. Rev. B 83 245132
Google Scholar
[45] Fu L, Kane C L 2009 Phys. Rev. B 79 161408
Google Scholar
[46] Lu S, Yu J 2019 Phys. Rev. A 99 033621
Google Scholar
[47] Turner A M, Zhang Y, Vishwanath A 2010 Phys. Rev. B 82 241102
Google Scholar
[48] Bansil A, Lin S, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[49] Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319
Google Scholar
[50] Barends R, Kelly J, Megrant A, Sank D, Jeffrey E, Chen Y, Yin Y, Chiaro B, Mutus J, Neill C, O'Malley P, Roushan P, Wenner J, White T C, Cleland A N, Martinis J M 2013 Phys. Rev. Lett. 111 080502
Google Scholar
[51] Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O'Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2016 Nature 508 500
[52] Steffen M, Ansmann M, McDermott R, Katz N, Bialczak R C, Lucero E, Neeley M, Weig E M, Cleland A N, Martinis J M 2006 Phys. Rev. Lett. 97 050502
Google Scholar
[53] Dziarmaga J 2005 Phys. Rev. Lett. 95 245701
Google Scholar
[54] Ezawa M 2018 Phys. Rev. B 98 205406
Google Scholar
[55] Chang P Y 2018 Phys. Rev. B 97 224304
Google Scholar
[56] Qiu X, Deng T S, Hu Y, Xue P, Yi W 2018 arXiv: 1806.10268
[57] Wang K, Qiu X, Xiao L, Zhan X, Bian Z, Sanders B C, Yi W, Xue P 2018 Nat. Commun. 10 2293
[58] 邓天舒, 易为 2019 68 040303
Google Scholar
Deng T S, Yi W 2019 Acta Phys. Sin. 68 040303
Google Scholar
-
图 1 (a) 每个截面对应固定动量, 截面内的极角对应于时间. 橘黄色的环代表
$k=0$ 和$2{\text{π}} $ , 它们粘合起来组成了$T^2$ ; (b) 如果动量空间中存在一些不动点$k_1$ ,$k_2$ , 截面的时间可连续收缩为一个点, 动量时间流形约化成一系列球面[21]Figure 1. (a) For any fixed momentum k, the cross section can be viewed as a circle
$S^1$ where the azimuthal angle represents the time t. After gluing$k=0$ and$k = 2{\text{π}} $ (saffron circles), the topology of the momentum-time manifold becomes$T^2$ ; (b) if there are two fixed points$k=k_1$ and$k_2$ , the corresponding circle contracts to a point, then the momentum-time manifold reduces to a series of spheres$S^2$ [21].
图 2 (a) SSH模型, 初态
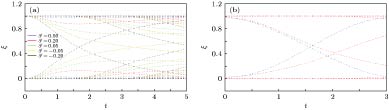
$\delta^{\rm i}=1$ 为拓扑平庸的, 末态$\delta^{\rm f}$ 取不同的值. 仅当末态为拓扑非平庸时, 纠缠谱在$1/2$ 处有交叉; (b)扩展的SSH模型, 次次次近邻跃迁具有相位, 系统属于AIII类. 蓝色的线代表用平带化的哈密顿量进行动力学演化, 红色的线代表由真实末态哈密顿量进行演化. 可以看出能带的色散打开了纠缠谱的能隙Figure 2. (a) In SSH model, the initial state of
$\delta^{\rm i}=1$ is topologically trivial, evolution of entanglement spectrum for different post-quenched$\delta^{\rm f}{\rm{s}}$ are shown with different colors. If and only if the post-quenched Hamiltonian is topologically nontrivial, the entanglement spectrum can cross at$1/2$ ; (b) in Extended SSH model, the third-nearest-neighbor hopping carries a phase factor, and the Hamiltonian belongs to class AIII. The blue curve shows the dynamics of entanglement spectrum evolved by flattened Hamiltonian, and the red curve shows the dynamics evolved by entanglement spectrum of real Hamiltonian. It can be seen that the band dispersion opens the gap of entanglement spectrum.
图 3 (a)实验过程序列示意图. 对每一个动量k, 初始时刻通过脉冲
$A_0\cos(\omega t+\phi_0)$ 制备初态, 而后通过改变外加的脉冲的$A_k$ 和$\phi_k$ 实现淬火动力学. (b), (c) 不同动量k对应的Bloch矢量的演化. 红色的星为实验的数据, 黄色的环为数值计算的数据. (b)初态$h^{\rm i}=0.2$ , 末态$h^{\rm f}=1.5$ . (c) 初态$h^{\rm i}=0.2$ , 末态$h^{\rm f}=0.5$ [22]Figure 3. The scheme of experiment control sequence. The initial state is prepared at the state-initialization period by control quantity
$A_0\cos(\omega t+\phi_0)$ for a fixed momentum k. Then for a quantum quench, by controlling$A_k$ and$\phi_k$ , we adjust the direction of the rotation axis. (b), (c) the evolution of Bloch vectors for different momenta. The red points and yellow rings are experimental and numerical datas. (b) pre-quenched parameter$h^{\rm i}=0.2$ , post-quench parameter$h^{\rm f}=1.5$ . (c) pre-quenched parameter$h^{\rm i}=0.2$ , post-quench parameter$h^{\rm f}=0.5$ .表 1 母哈密顿量
$\tilde{h}(k, t)$ 的拓扑分类. TRS、PHS、CS分别是时间反演对称性, 粒子空穴对称性和手征对称性. s, t, d,$d_{//}$ , 额外对称性P参见文献[37]; original class是没有额外对称性时系统的拓扑分类.$K_{\rm C}^{\rm U/A}(K_{\rm R}^{\rm U/A})$ 是系统的K群. Dynamical realization表示在淬火动力学中存在的拓扑分类. Stable against dispersion指能带存在色散时纠缠谱交叉能够稳定存在的拓扑分类Table 1. Topological classification of parent Hamiltonian. TRS, PHS and CS represent the time reversal symmetry, particle hole symmetry and chorial symmetry, respectively. The definition of s, t, d,
$d_{//}$ and additional symmetry P can be found in Ref.[37]. Original class represents the topological classification without additional symmetry.$K_{\rm C}^{\rm U/A}(K_{\rm R}^{\rm U/A})$ is the K group. Dynamical realization means the topological classes which can be realized in quench dynamics. Stable against dispersion means entanglement spectrum crossing which is stable against band dispersion.AZ class TRS PHS CS $(s, t, d, d_{//}, \text{original~class,} P)$ $K_{\rm C}^{\rm U/A}(K_{\rm R}^{\rm U/A})$ Dynamical realization Stable against dispersion A 0 0 0 $(\sim, \sim, 2, \sim, A, \sim)$ ${\mathbb Z}$ 0 0 AIII 0 0 1 $(0, 1, 2, 1, A, \bar{U})$ ${\mathbb Z}\bigoplus{\mathbb Z}$ ${\mathbb Z}$ 0 AI 1 0 0 $(\sim, \sim, 2, \sim, AI, \sim)$ 0 0 0 BDI 1 1 1 $(0, 3, 2, 1, AI, \bar{A}_{+}^{+})$ ${\mathbb Z}$ ${\mathbb Z}$ ${\mathbb Z}_2$ D 0 1 0 $(2, \sim, 2, 1, A, \bar{A}^{+})$ ${\mathbb Z}_2$ ${\mathbb Z}_2$ ${\mathbb Z}_2$ DIII –1 1 1 $(4, 1, 2, 1, AII, \bar{A}_{+}^{+})$ ${\mathbb Z}_2\bigoplus{\mathbb Z}_2$ ${\mathbb Z}_2$ 0 AII –1 0 0 $(\sim, \sim, 2, \sim, AII, \sim)$ ${\mathbb Z}_2$ 0 0 CII –1 –1 1 $(4, 3, 2, 1, AII, \bar{A}_{+}^{-})$ ${\mathbb Z}$ ${\mathbb Z}$ 0 C 0 –1 0 $(6, \sim, 2, 1, A, \bar{A}^{-})$ 0 0 0 CI 1 –1 1 $(0, 1, 2, \sim, AI, \bar{A}_{+}^{-})$ 0 0 0 
DownLoad: CSV
-
[1] Klitzing K V, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Thouless D J, Kohmoto M, Nightingale M P, Nijs M den Nijs 1982 Phys. Rev. Lett. 49 405
Google Scholar
[3] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[4] Qi X, Zhang S 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[5] Chiu C, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005
Google Scholar
[6] Atala M, Aidelsburger M, Barreiro J T, Abanin D, Kitagawa T, Demler E, Bloch I 2013 Nat. Phys. 9 795
Google Scholar
[7] Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, Esslinger T 2014 Nature (London)
515 237 Google Scholar
[8] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y, Chen S, Liu X J, Pan J W 2016 Science 354 83
Google Scholar
[9] Aidelsburger M, Atala M, Lohse M, Barreiro J T, Paredes B, Bloch I 2013 Phys. Rev. Lett. 111 185301
Google Scholar
[10] Aidelsburger M, Lohse M, Schweizer C, Atala M, Barreiro J T, Nascimbne S, Cooper N R, Bloch I, Goldman N 2015 Nat. Phys. 11 162
Google Scholar
[11] Miyake H, Siviloglou G A, Kennedy C J, Burton W C, Ketterle W 2013 Phys. Rev. Lett. 111 185302
Google Scholar
[12] Caio M D, Cooper N R, Bhaseen M J 2015 Phys. Rev. Lett. 115 236403
Google Scholar
[13] Alessio L D, Rigol M 2015 Nat. Commun. 6 8336
Google Scholar
[14] Hu Y, Zoller P, Budich J C 2016 Phys. Rev. Lett. 117 126083
[15] Wilson J H, Song J C W, Refael G 2016 Phys. Rev. Lett. 117 235032
[16] McGinley M, Cooper N R 2018 Phys. Rev. Lett. 121 090401
Google Scholar
[17] McGinley M, Cooper N R 2019 Phys. Rev. B 99 075418
Google Scholar
[18] Wang C, Zhang P, Chen X, Yu J, Zhai H 2017 Phys. Rev. Lett. 118 185701
Google Scholar
[19] Chen X, Wang C, Yu J 2019 arXiv: 1907.08840
[20] Tarnowski M, Unal F N, Flaschner N, Rem B S, Eckardt A, Sengstock K, Weitenberg C 2019 Nat. Commun. 10 1728
Google Scholar
[21] Yang C, Li L, Chen S 2018 Phys. Rev. B(R)
97 060304 Google Scholar
[22] Guo X Y, Yang C, Zeng Y, Peng Y, Li H K, Deng H, Jin Y R, Chen S, Zheng D N, Fan H 2019 Phys. Rev. Applied 11 044080
Google Scholar
[23] Gong Z, Ueda M 2018 Phys. Rev. Lett. 121 250601
Google Scholar
[24] Zhang L, Zhang L, Niu S, Liu X J 2018 Science Bulletin 63 1385
Google Scholar
[25] Zhang L, Zhang L, Liu X J 2019 Phys. Rev. A 99 053606
Google Scholar
[26] Zhang L, Zhang L, Liu X J 2019 arXiv: 1907.08840
[27] Sun W, Yi C R, Wang B Z, Zhang W W, Sanders B C, Xu X T, Wang Z Y, Schmiedmayer J, Deng Y J, Liu X J, Chen S, Pan J W 2019 Phys. Rev. Lett. 121 250403
[28] Lieb E H, Robinson D W 1972 Commun. Math. Phys. 28 251
Google Scholar
[29] Gong Z, Kura N, Sato M, Ueda M 2019 arXiv: 1904.12464
[30] Altland A, Zirnbauer M R 1997 Phys. Rev. B 55 1142
Google Scholar
[31] Schnyder A P, Ryu S, Furusaki A, Ludwig A W W 2008 Phys. Rev. B 78 2208
[32] Kitaev A 2009 AIP Conf. Proc. 22 1134
[33] Kitaev A 2001 Ann. Phys. (NY)
303 2 [34] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[35] Li L, Yang C, Chen S 2016 Eur. Phys. J. B 89 195
Google Scholar
[36] Teo J C Y, Kane C L 2010 Phys. Rev. B 82 115120
Google Scholar
[37] Shiozaki K, Sato M 2014 Phys. Rev. B 90 165114
Google Scholar
[38] Chiu C K, Yao H, Ryu S 2013 Phys. Rev. B 88 075142
Google Scholar
[39] Fu L, Kane C 2006 Phys. Rev. B 74 195312
Google Scholar
[40] Moore J E, Balents L 2007 Phys. Rev. B(R)
75 121306 Google Scholar
[41] Wen X G 1992 Int. J. Mod. Phys. B 06 1711
Google Scholar
[42] Fidkowski L 2010 Phys. Rev. Lett. 104 130502
Google Scholar
[43] Peschel I 2002 J. Phys. A 36 L205
[44] Hughes T L, Prodan E, Bernevig B A 2011 Phys. Rev. B 83 245132
Google Scholar
[45] Fu L, Kane C L 2009 Phys. Rev. B 79 161408
Google Scholar
[46] Lu S, Yu J 2019 Phys. Rev. A 99 033621
Google Scholar
[47] Turner A M, Zhang Y, Vishwanath A 2010 Phys. Rev. B 82 241102
Google Scholar
[48] Bansil A, Lin S, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[49] Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319
Google Scholar
[50] Barends R, Kelly J, Megrant A, Sank D, Jeffrey E, Chen Y, Yin Y, Chiaro B, Mutus J, Neill C, O'Malley P, Roushan P, Wenner J, White T C, Cleland A N, Martinis J M 2013 Phys. Rev. Lett. 111 080502
Google Scholar
[51] Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O'Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2016 Nature 508 500
[52] Steffen M, Ansmann M, McDermott R, Katz N, Bialczak R C, Lucero E, Neeley M, Weig E M, Cleland A N, Martinis J M 2006 Phys. Rev. Lett. 97 050502
Google Scholar
[53] Dziarmaga J 2005 Phys. Rev. Lett. 95 245701
Google Scholar
[54] Ezawa M 2018 Phys. Rev. B 98 205406
Google Scholar
[55] Chang P Y 2018 Phys. Rev. B 97 224304
Google Scholar
[56] Qiu X, Deng T S, Hu Y, Xue P, Yi W 2018 arXiv: 1806.10268
[57] Wang K, Qiu X, Xiao L, Zhan X, Bian Z, Sanders B C, Yi W, Xue P 2018 Nat. Commun. 10 2293
[58] 邓天舒, 易为 2019 68 040303
Google Scholar
Deng T S, Yi W 2019 Acta Phys. Sin. 68 040303
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 11925
- PDF Downloads: 422
- Cited By: 0
