-
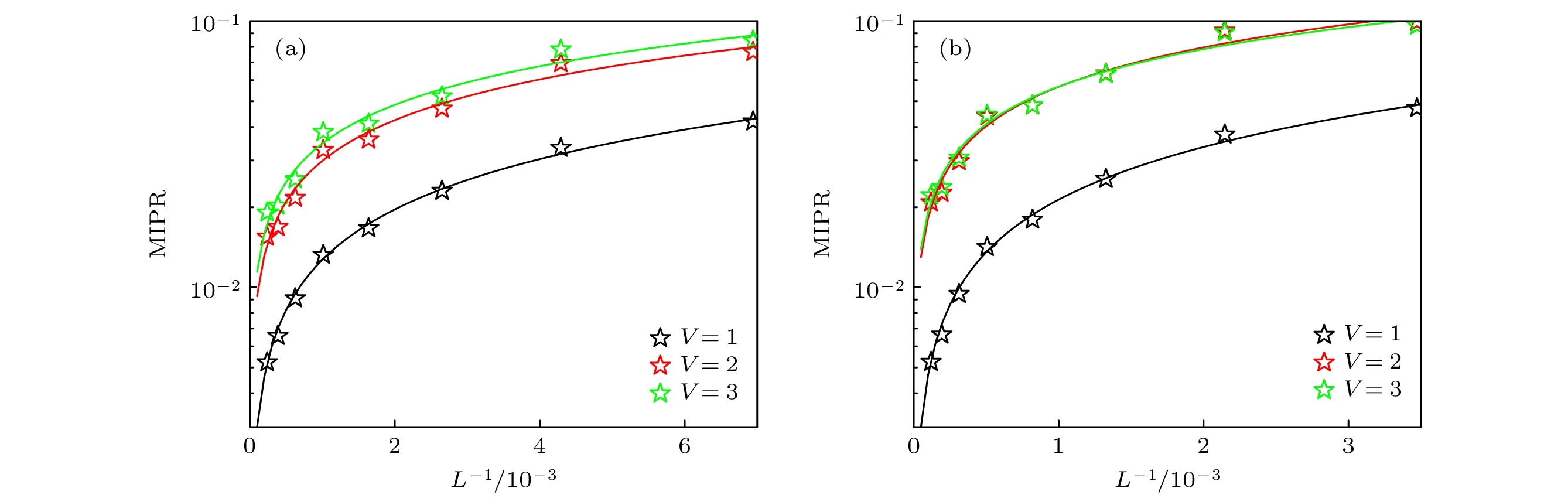
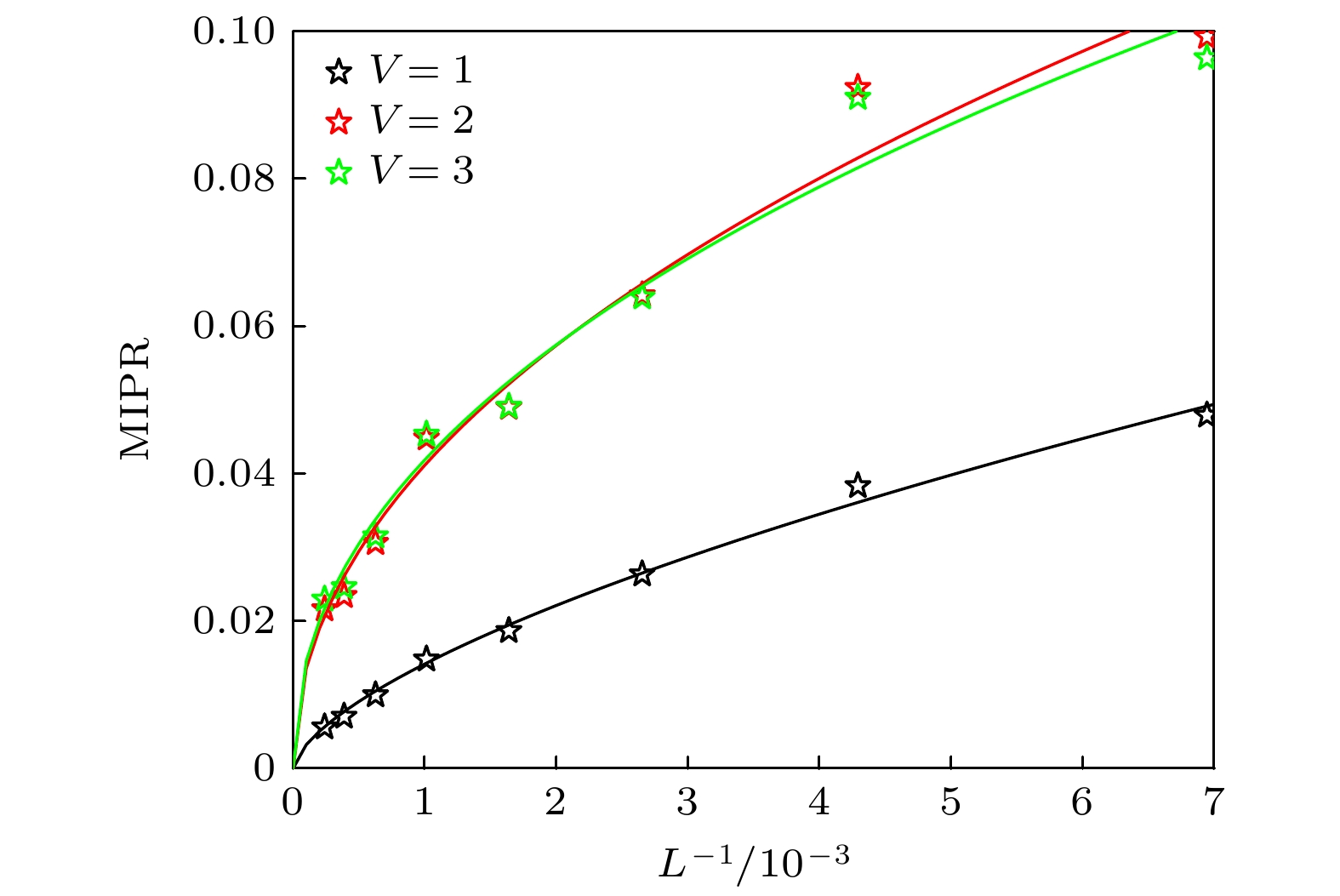
This paper investigates the topological phase transitions and localization properties in a 1D p-wave superconductor under Fibonacci quasi-periodic potential modulation. By calculating the $Z_2$ topological invariant, we numerically determine the topological phase diagram of the system. We find that, under Fibonacci quasi-periodic modulation, the system can transition from a topologically trivial phase to a topological Anderson superconductor phase. Moreover, under certain parameters, the system undergoes multiple topological Anderson superconductor phases transitions, accompanied by the emergence of zero-energy modes. However, in the case of strong disorder, the topological Anderson superconductor phase is destroyed, indicating that the topological Anderson superconductor phase can only be induced within a finite range of parameters. Furthermore, by calculating and analyzing the fractal dimension and the mean inverse participation ratio (MIPR) order parameter, we analyze the localization properties of the system. The results show that regardless of the increase in disorder strength, the fractal dimension values of most eigenstates always remain within the range $(0,1)$. Subsequently, the variations in the fractal dimensions of all eigenstates for different system sizes were studied. The results show that the fractal dimension values of most eigenstates are away from $0$ and $1$. These results indicate that the wavefunction in the bulk of the topological Anderson superconductor phase induced by Fibonacci quasi-periodic potential are critical state wavefunction, with the system overall being in a critical phase. The stability of the critical phase is confirmed by scale behavior of MIPR, as shown in Fig. (a). It differs from the traditional topological Anderson superconductor phase induced by random disorder or AA-type quasi-periodic disorder. The results provide new insights and references for the study of topological phase transitions and localization transitions in 1D p-wave superconductors. 
-
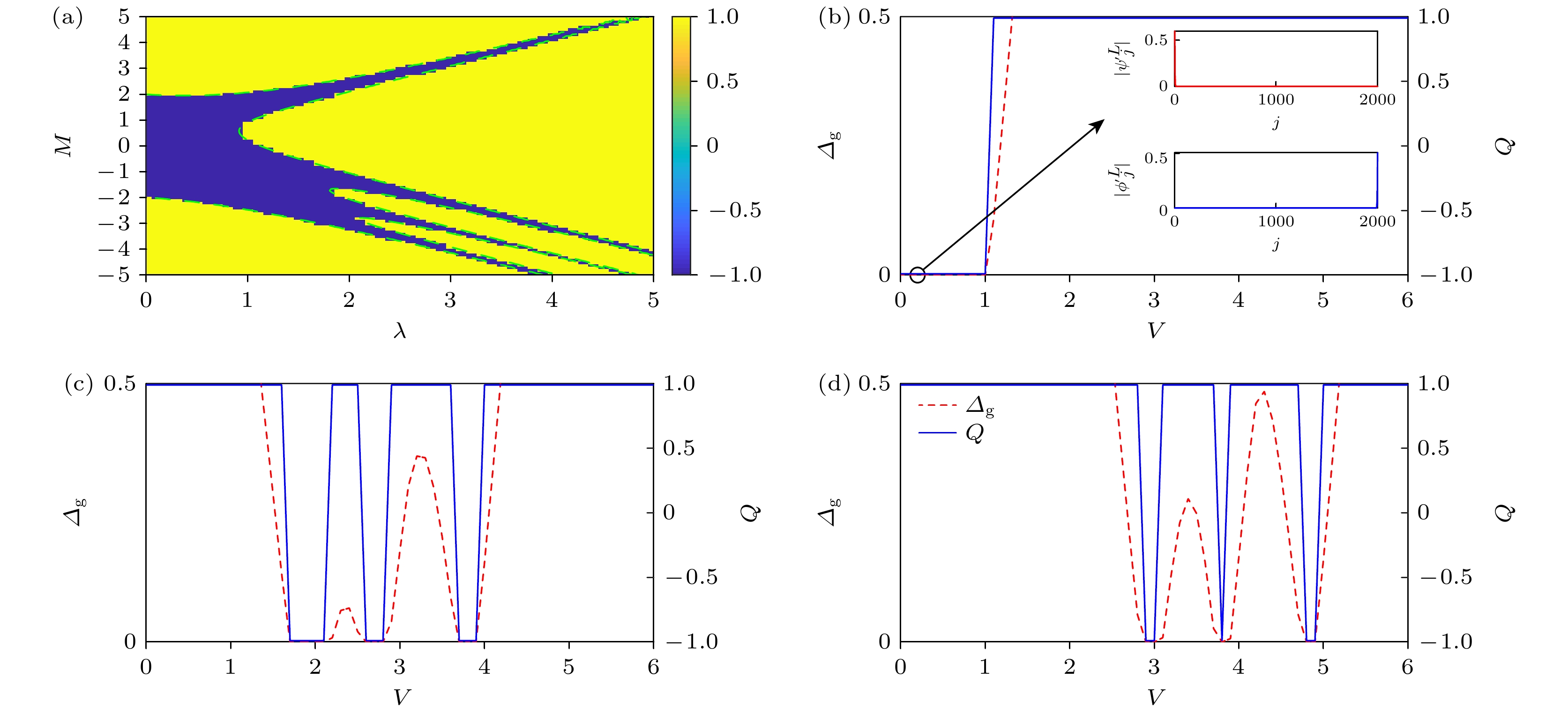
图 1 (a)以拓扑不变量 Q大小为背景颜色填充的 V- M参数平面的拓扑相图. 颜色条代表 $Z_{2}$拓扑不变量 Q的大小. 绿色虚线代表拓扑相变点解析解, 由( 20)式确定. (b)—(d) 当常数势强度 $M=1$, $-3$和 $-4$时, 能隙 $\Delta_g$和 $Z_{2}$拓扑不变量 Q随着无序强度 V的变化. (b)插图中对应的无序强度 $V=0.2$时, L能级对应的波函数分布. 这里, $\Delta=0.4$和 $L=2000$
Figure 1. The $Z_{2}$ topological invariant Q as a function of the disorder strength V and constant potential M. The colorbar shows the value of the $Z_{2}$ topological invariant Q. The green dashed line represents the analytical solution of the topological phase transition point, determined by Eq. ( 20). Energy gap $\Delta_g$ and the $Z_{2}$ topological invariant Q as a function of V for (b) $M=1$, (c) $M=-3$ and (d) $M=-4$. The wave function distributions corresponding to the L energy levels at a disorder strength of $V=0.2$ in the inset of (b). Other parameters: $\Delta=0.4$ and $L=2000$.
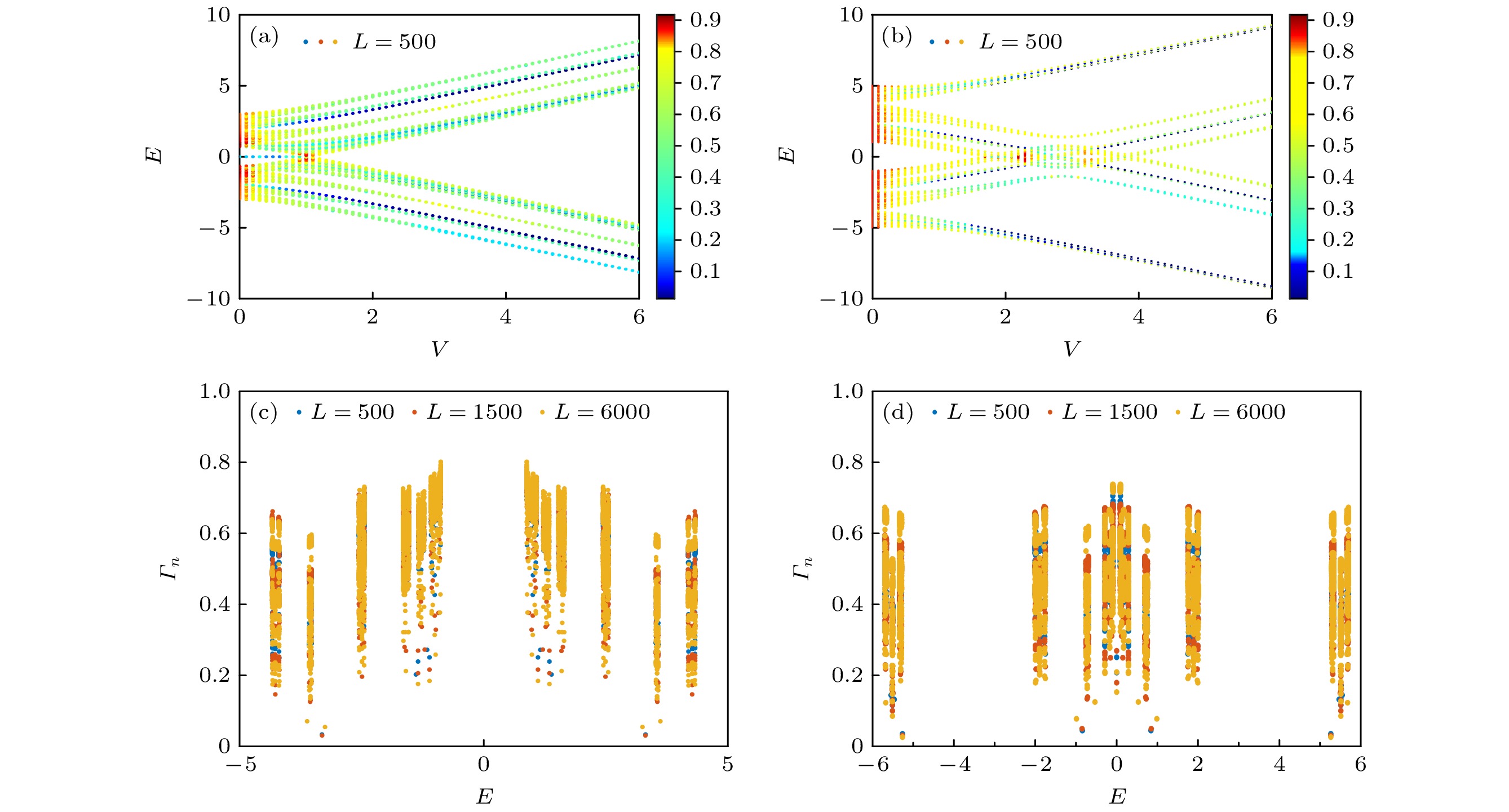
图 2 当系统尺寸 $L=500$, M分别为(a) $M=1$和(b) $M=-3$时, 分形维度( ${\Gamma}_n$)随着本征能量 E和无序强度 V的变化. 图中的颜色条代表分形维度( ${\Gamma}_n$)的大小. (c)当 $V=2$且 $M=1$时, 不同系统尺寸下, 系统分形维度( ${\Gamma}_n$)的值. (d)当 $V=2$且 $M=-3$时, 不同系统尺寸下, 系统分形维度( ${\Gamma}_n$)的值. 其他参数: $\Delta=0.4$
Figure 2. The fractal dimension ${\Gamma}_n$ of different eigenstates as a function of the corresponding E and the modulation strength V with $L=500$ for (a) $M=1$ and (b) $M=-3$. (c) The Fractal dimensions ${\Gamma}_n$ for different system sizes for $V=2$ and $M=1$. (d) The Fractal dimensions ${\Gamma}_n$ for different system sizes for $V=2$ and $M=-3$. Other parameters: $\Delta=0.4$.
图 3 当 M分别为(a) $M=1$和(b) $M=-3$时, MNPR在无序强度为 $V=1$, $2$ 和 $3$情况下的标度行为. 其他参数: $\Delta=0.4$
Figure 3. The scaling behavior of MIPR in (a) $M=1$ and (b) $M=-3$ with $V=1, 2$ and $3$. Other parameters: $\Delta=0.4$.
-
[1] Nakajima S, Takei N, Sakuma K, Kuno Y, Marra P, Takahashi Y 2021 Nat. Phys. 17 844
Google Scholar
[2] Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[3] Hasan M X and Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[4] Qi X L and Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[5] Bansil A, Lin H, T. Das 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[6] Xiao T, Xie D, Dong Z, Chen T, Yi W, Yan B 2021 Sci. Bull. 66 2175
Google Scholar
[7] Szameit A and Rechtsman M C 2024 Nat. Phys. 20 905
Google Scholar
[8] König M, Wiedmann S, Brüne C, Roth A, Buhmann H, Molenkamp L, Qi X L, Zhang S C 2007 Science 318 766
Google Scholar
[9] Zhang H J, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438
Google Scholar
[10] Zhang Y Y, Chu R L, Zhang F C, Shen S Q 2012 Phys. Rev. B 85 035107
Google Scholar
[11] Jiang H, Wang L, Sun Q f, Xie X C 2009 Phys. Rev. B 80 165316
Google Scholar
[12] Li X Q, Zhang H H, Xu H, San H D, Wang X N, Qi S F, Qiao Z H 2024 Phys. Rev. B 109 155427
Google Scholar
[13] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[14] Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801
Google Scholar
[15] Velury S, Bradlyn B, Hughes T L 2021 Phys. Rev. B 103 024205
Google Scholar
[16] 徐磊, 李沛岭, 吕昭征, 沈洁, 屈凡明, 刘广同, 吕力 2023 72 177401
徐磊, 李沛岭, 吕昭征, 沈洁, 屈凡明, 刘广同, 吕力 2023 72 177401
[17] 关欣, 陈刚 2023 72 140301
Google Scholar
Guan X, Chen G 2023 Acta Phys. Sin. 72 140301
Google Scholar
[18] Gu Y, Lu Z P 2024 Chin. Phys.B 33 090202
Google Scholar
[19] Li G Q, Wang B H, Tang J Y, Peng P, Dong L W 2023 Chin. Phys. B 32 077102
Google Scholar
[20] Huang A H, Ke S S, Guan J H, Li J, Lou W K 2024 Chin. Phys. Lett. 41 097302
Google Scholar
[21] Chang Z W, Hao W C, Bustamante M, Liu X 2024 Chin. Phys. Lett. 41 037302
Google Scholar
[22] Xu Z, Zhang R, Chen S, Fu L, Zhang Y 2020 Phys. Rev. A 101 013635
Google Scholar
[23] Prodan E, Hughes T L, Bernevig B A 2010 Phys. Rev. Lett. 105 115501
Google Scholar
[24] Cai X, Lang L J, Chen S, Wang Y 2013 Phys. Rev. Lett. 110 176403
Google Scholar
[25] Liu J, Potter A C, Law K T, Lee P A 2012 Phys. Rev. Lett. 109 267002
Google Scholar
[26] Li J, Chu R L, Jain J K, Shen S Q 2009 Phys. Rev. Lett. 102 136806
Google Scholar
[27] Groth C W, Wimmer M, Akhmerov A R, Tworzydlo J, Beenakker C W J 2009 Phys. Rev. Lett. 103 196805
Google Scholar
[28] Meier E J, An F A, Dauphin A, Maffei M, Massignan P, Hughes T L, Gadway B 2018 Science 362 929
Google Scholar
[29] Stützer S, Plotnik Y, Lumer Y, Titum P, Lindner N H, Segev M, Rechtsman M C, Szameit A 2018 Nature (London) 560 461
Google Scholar
[30] Borchmann J, Farrell A, Pereg-Barnea T 2016 Phys. Rev. B 93 125133
Google Scholar
[31] Kitaev A Y 2001 Phys. Usp. 44 131
Google Scholar
[32] Ivanov D A 2001 Phys. Rev. Lett. 86 268
Google Scholar
[33] Zhu S L, Shao L B, Wang Z D, Duan L M 2011 Phys. Rev. Lett. 106 100404
Google Scholar
[34] Lindner N H, Berg E, Refael G, Stern A 2012 Phys. Rev. X 2 041002
[35] Nayak C, Simon S H, Stern A, Freedman M, Sarma S D 2008 Rev. Mod. Phys. 80 1083
Google Scholar
[36] Lang L J, Chen S 2012 Phys. Rev. B. 86 205135
Google Scholar
[37] Cai X M, Lang L J, Chen S, Wang Y P 2013 Phys. Rev. Lett. 110 176403
Google Scholar
[38] Hua C B, Chen R, Xu D H, Zhou B 2019 Phys. Rev. B 100 205302
Google Scholar
[39] Hegde S S, Vishveshwara S 2016 Phys. Rev. Lett. 94 115166
[40] DeGottardi W, Thakurathi M, Vishveshwara S, Sen D 2013 Phys. Rev. B 88 165111
Google Scholar
[41] Wakatsuki R, Ezawa M, Tanaka Y, Nagaosa N 2014 Phys. Rev. B 90 014505
Google Scholar
[42] Jagannathan A 2021 Rev. Mod. Phys. 93 045001
Google Scholar
[43] Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 18
[44] Merlin R, Bajema K, Clarke R, Juang F Y, Bhattacharya P K 1985 Phys. Rev. Lett. 55 1768
Google Scholar
[45] Longhi S 2019 Phys. Rev. Lett. 122 237601
Google Scholar
[46] Kobiałka A, Awoga O A, Leijnse M, Domański T, Holmvall P, Black-Schaffer A M 2024 Phys. Rev. B 110 134508
Google Scholar
[47] Hu Y C, Kane C L 2018 Phys. Rev. Lett. 120 066801
Google Scholar
[48] Tong L, Cheng S J, Guo H, Gao X L 2021 Phys. Rev. B 103 104203
Google Scholar
[49] Zhu J X 2016 Bogoliubov-de Gennes Method and Its Applications (Lecture Notes in Physics 924
[50] Lieb E, Schultz T, Mattis D 1961 Ann. Phys. 16 407
Google Scholar
[51] P. Zhang and F. Nori 2016 New J. Phys. 18 043033
Google Scholar
[52] Akhmerov A R, Dahlhaus J P, Hassler F, Wimmer M, Beenakker C W J 2011 Phys. Rev. Lett. 106 057001
Google Scholar
[53] Fulga I C, Hassler F, Akhmerov A R, Beenakker C W J 2011 Phys. Rev. B 83 155429
Google Scholar
[54] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803
Google Scholar
[55] Li X, Sarma S D 2020 Phys. Rev. B 101 064203
Google Scholar
[56] Wang Y, Zhang L, Niu S, Yu D, Liu X J 2020 Phys. Rev. Lett. 125 073204
Google Scholar
[57] Longhi S 2020 Opt. Lett. 45 4036
Google Scholar
[58] Lang L J, Cai X M, Chen S 2012 Phys. Rev. Lett. 108 220401
Google Scholar
[59] Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 1003
Google Scholar
[60] Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001
Google Scholar
[61] Lin C H, Sau J D, Das Sarma S 2012 Phys. Rev. B 86 224511
Google Scholar
[62] Prada E, San Jose P, Aguado R 2012 Phys. Rev. B 86 180503
Google Scholar
[63] Nichele F, Drachmann A C C, Whiticar A M, O $\acute{\rm{F}}$arrell E C T, Suominen H J, Fornieri A, Wang T, Gardner G C, Thomas C, Hatke A T, Krogstrup P, Manfra M J, Flensberg K, Marcus C M 2017 Phys. Rev. Lett. 119 136803
Google Scholar
[64] Kells G, Meidan D, Brouwer P W 2012 Phys. Rev. B 85 060507
Google Scholar
[65] Chen J, Woods B D, Yu P, Hocevar M, Car D, Plissard S R, Bakkers E P A M, Stanescu T D, Frolov S M 2019 Phys. Rev. Lett. 123 107703
Google Scholar
[66] Yu P, Chen J, Gomanko M, Badawy G, Bakkers E P A M, Zuo K, Mourik V, Frolov S M 2021 Nat. Phys. 17 482
Google Scholar
DownLoad:
Metrics
- Abstract views: 499
- PDF Downloads: 21
- Cited By: 0
