-
构建了二维六角蜂窝晶格的两种结构, 让散射体和基体材料反转. 由于特有的点群对称, 该晶格在布里渊区中心具有类比电子体系的p轨道和d轨道. 在散射体和基体反转的两种结构中, p轨道和d轨道也直接实现了反转. 定量分析了产生轨道反转的原因来自于低频局域共振产生空气带和介质带的反转. 通过p轨道和d轨道的宇称特性, 构建了类比电子体系量子自旋霍尔效应的赝自旋态. 通过Γ点处有效哈密顿量的分析, 揭示轨道反转导致的拓扑相变. 通过结构的优化, 构建了基于赝自旋的拓扑边界态. 电磁波仿真模拟和能流矢量分析证明了结构具有电子体系量子自旋霍尔效应的特性, 即自旋与传播方向锁定和拓扑保护. 结果也证明经典波量子自旋霍尔效应的实现可以不经历带隙关闭的过程. 与同类型的研究相比较, 本文的结构不需要晶格的缩放, 具有设计简单、带隙宽和边界态局域性较强的特点.Two kinds of two-dimensional photonic crystal with hexagonal honeycomb lattices are constructed in which the scatterer and the matrix materials are reversed. Due to the symmetry of special point group, the lattices have p and d orbitals in the center of Brillouin region, which are similar to those in the electronic system. With the structure reversal, the p and d orbitals are also directly inverted. Quantitative analysis shows that the orbital inversion is due to the inversion of air band and medium band because of the local resonance effect in the low frequency bands. Based on the parity properties of p and d orbitals, the pseudo spin states are constructed by analogy to the quantum spin Hall effect in electronic systems. The analysis of the effective Hamiltonian at Γ point shows that the topological phase transition caused by orbital inversion is revealed. The pseudo spin edge states construct an optimal structure. The electromagnetic wave simulations and energy flow vector analysis show that the structure edge takes on the properties of quantum spin Hall effect, namely, the propagation direction is locked by the spin direction and the propagation is topologically protected. The results also show that the quantum spin Hall effect can be realized without undergoing the closing of gap. The comparison among similar researches indicates that the realization of the pseudo spin states does not need the deformation of lattice, and the structure proposed in this work possesses the characteristics of simple design, wide band gap and strong edge localization.
-
Keywords:
- photonic crystal /
- structure reversal /
- band reversal /
- topology transition /
- pseudospin
[1] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[2] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[3] Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[4] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
Google Scholar
[5] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[6] Sheng L, Sheng D N, Ting C S, Haldane F D M 2005 Phys. Rev. Lett. 95 136602
Google Scholar
[7] Wang Z, Chong Y D, Joannopoulos J D, et al. 2009 Nature 461 772
Google Scholar
[8] Wang Z, Chong Y D, Soljačić M 2008 Phys. Rev. Lett. 100 013905
Google Scholar
[9] Fang Y T, He H Q, Hu J X, Wen Z 2016 Phys. Rev. A 91 033827
Google Scholar
[10] Fang Y T, He H Q, Hu J X 2016 IEEE J. Sel. Top. Quant. 22 4901109
Google Scholar
[11] Lu L, Joannopoulos J D, Soljaˇci′c M 2014 Nat. Photonics 8 821
Google Scholar
[12] 孙晓晨, 何程, 卢明辉, 陈延峰 2017 66 224203
Google Scholar
Sun X C, He C, Lu M H, Chen Y F 2017 Acta Phys. Sin. 66 224203
Google Scholar
[13] 王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延峰 2019 68 224206
Google Scholar
Wang H F, Xie B Y, Zhan P, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 224206
Google Scholar
[14] Skirlo S A, Lu L, Soljačić M 2014 Phys. Rev. Lett. 113 113904
Google Scholar
[15] Khanikaev A B, Mousavi S H, Tse W K, Kargarian M, MacDonald A H, Shvets G 2013 Nat. Mater. 12 233
Google Scholar
[16] He C, Sun X C, Liu X P, Lu M H, Chen Y, Feng L, Chen Y F 2016 Proc. Natl. Acad. Sci. USA 113 4924
Google Scholar
[17] Guo Z W, Jiang H T, Long Y, Yu K, Ren J, Xue C H, Chen H 2017 Sci. Rep. 7 7742
Google Scholar
[18] Bisharat D J, Sievenpiper D F 2019 Laser Photonics Rev. 13 1900126
Google Scholar
[19] Wu L H, Hu X 2015 Phys. Rev. Lett. 114 223901
Google Scholar
[20] Li Y, Sun Y, Zhu W W, Guo Z W, Jiang J, Kariyado T, Chen H, Hu X 2018 Nat. Commun. 9 4598
Google Scholar
[21] Huang X Q, Yang Y T, Hang Z H, Zhang Z Q, Chan C T 2016 Phys. Rev. B 93 085415
Google Scholar
[22] Xu L, Wang H X, Xu Y D, Chen H Y, Jiang J H 2016 Opt. Express 24 18059
Google Scholar
[23] Mei J, Chen Z G, Wu Y 2016 Sci. Rep. 6 32752
Google Scholar
[24] Gao Y F, Jiang Z and Zhang L L, et al. 2018 J. Appl. Phys. 124 213107
Google Scholar
[25] 王键, 吴世巧, 梅军 2017 66 224301
Google Scholar
Wang J, Wu S Q, Mei J 2017 Acta Phys. Sin. 66 224301
Google Scholar
[26] 贾鼎, 葛勇, 袁寿其, 孙宏祥 2019 68 224301
Google Scholar
Jia D, Ge Y, Yuan S Q, Sun H X 2019 Acta Phys. Sin. 68 224301
Google Scholar
[27] Xia B Z, Fan H Y, Liu T T 2019 Int. J. Mech. Sci. 155 197
Google Scholar
[28] Yang Y T, Xu Y F, Xu T, Wang H X, Jiang J H, Hu X, Hang Z H 2018 Phys. Rev. Lett. 120 217401
Google Scholar
[29] Yang Y H, Sun H X, Xia J P, Xue H R, Guo Z, Ge Y, Jia D, Yuan S Q, Chong Y D, Zhang B L 2019 Nat. Phys. 15 645
Google Scholar
[30] John D J, Steven G J, Robert D M 2008 Photonic Crystals Molding the Flow of Light (2nd Ed.) (Princeton: Princeton University Press) pp46–49
[31] 温熙森, 温激鸿, 郁殿龙, 王刚, 刘耀宗, 韩小云 2009 声子晶体 (北京: 国防工业出版社) 第8页
Wen X S, Wen J H, Yu D L, Wang G, Liu Y Z, Han X Y 2009 Phononic Crystals (Beijing: National Defense Industry Press) p8 (in Chinese)
[32] Lemoult F, Kaina N, Fink M, Lerosey 2013 Nat. Phys. 9 55
Google Scholar
[33] Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757
Google Scholar
[34] Xia J P, Jia D, Sun H X, Yuan S Q, Ge Y, Si Q R, Liu X J 2018 Adv. Mater. 30 1805002
Google Scholar
[35] Jiang Z, Gao Y F, He L, Sun J P, Song H, Wang Q 2019 Phys. Chem. Chem. Phys. 21 11367
Google Scholar
[36] Ji C Y, Liu G B, Zhang Y Y, Zou B S, Yao Y G 2019 Phys. Rev. A 99 043801
Google Scholar
-
图 1 六角蜂窝晶格结构模型(六边形是原胞, a1和a2是晶格基矢) (a) A型结构, 散射体是空气柱, 基体是介质; (b) D型结构, 散射体是介质柱, 基体是空气; (c) 晶格第一布里渊区
Fig. 1. Schematic of hexagonal honeycomb lattice (the hexagon is the unit cell, and a1 and a2 are the basic vectors of lattice): (a) The scatterer and matrix are air rods and dielectric, respectively; (b) the scatterer and matrix are dielectric rods and air, respectively; (c) the first Brillouin zone.
图 2 两种结构的能带和在Γ点的p轨道和d轨道 (a) A型结构; (b) D型结构
Fig. 2. Band structures of the hexagonal honeycomb lattices, and the orbitals of p and d: (a) Type A; (b) type D.
图 3 p轨道和d轨道的频率随散射体材料介电常数
$ {\varepsilon _{\rm{s}}} $ 和基体体材料介电常数$ {\varepsilon _{\rm{m}}} $ 之差的变化Fig. 3. Frequency positions of p and d orbits with the differences of
$ {\varepsilon _{\rm{s}}} $ and$ {\varepsilon _{\rm{m}}} $ 
图 4 优化后两种结构的能带以及p轨道和d轨道的位置 (a) A型结构; (b) D型结构
Fig. 4. Band structures of the optimized lattices, and the orbitals of p and d: (a) Type A; (b) type D.
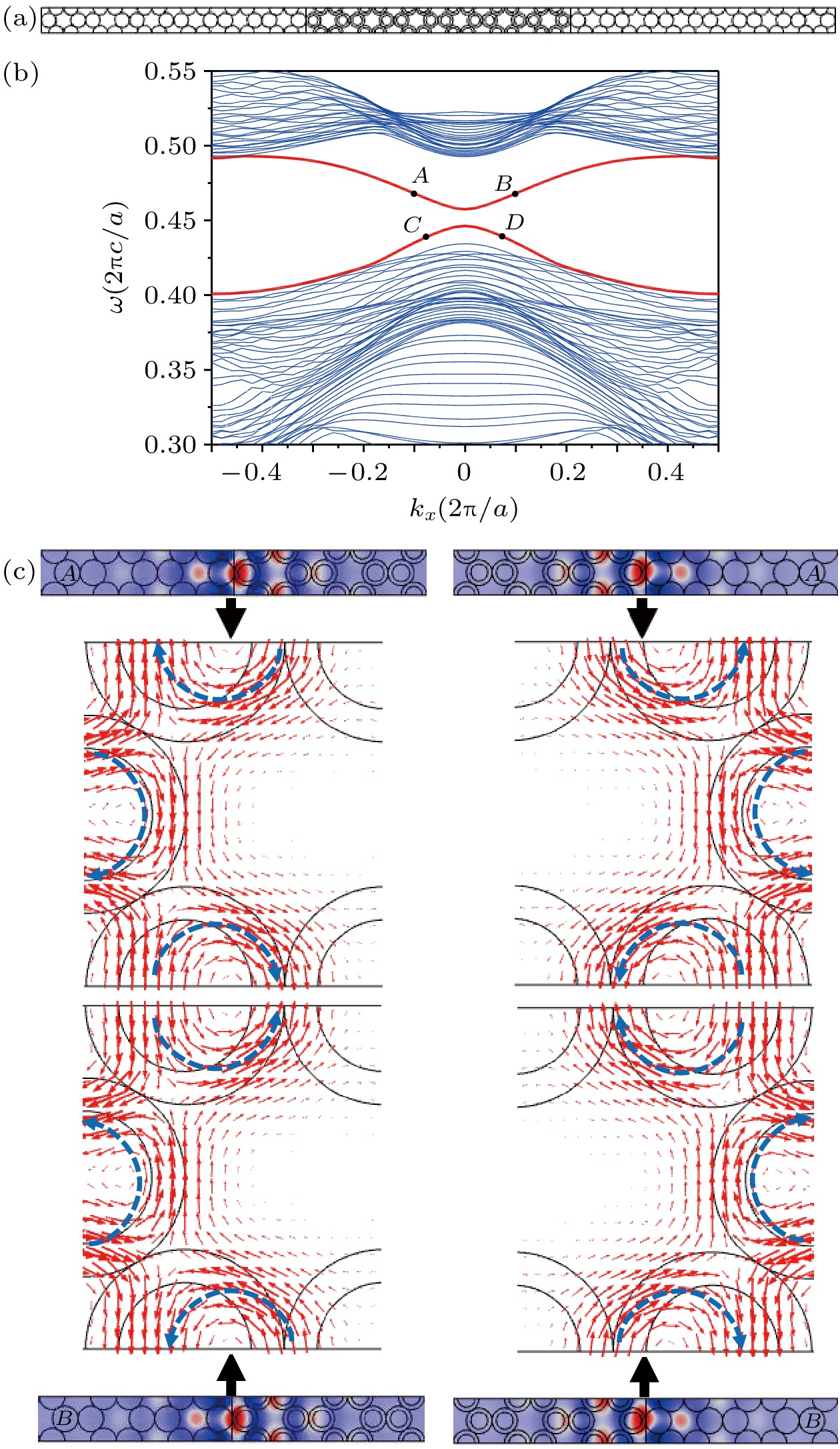
图 5 边界态的构建与分析 (a) 超胞; (b) 超胞的带结构; (c) 模式分析; 图(c)给出图(b)边界态A 和B两点在拓扑非平庸层(中间层)左、右两侧边界激发的模场Ez和边界靠非平庸层一侧的能流矢量, 它们分别对应不同旋转方向的赝自旋, 分别用旋转箭头表示; 由于边界处能流矢量比涡旋处能流矢量大很多, 为了看清矢量旋转方向, 将矢量图的位置向非平庸层方向进行了适当的偏离
Fig. 5. Construction and analysis of the edge states: (a) Supercell; (b) bands of the supercell; (c) mode analysis. The mode field Ez of the energy flow vectors of points A and B in (c) reveal the pseudo spins at the two edges of the middle non-trivial layer in (a). Because the energy flow vectors at the edge are much larger than those in the vortex, we move the vector plots to the non-trivial layer for a proper distance.
图 6 赝自旋源(白色六角星)激发的电磁波边界态传输 (a) 频率位置为AB, 逆时针自旋; (b) 频率位置为AB, 顺时针自旋; (c) 频率位置为CD, 逆时针自旋; (d) 频率位置为CD, 顺时针自旋
Fig. 6. Edge state transmission of electromagnetic wave excited by pseudospin source (white hexagon star): (a) Frequency position at AB and counterclockwise spin; (b) frequency position at AB and clockwise spin; (c) frequency position at CD and counterclockwise spin; (d) frequency position at CD and clockwise spin.
图 7 拓扑边界态鲁棒性的验证, 白色六角星为赝自旋源位置 (a) 电场Ez幅度的分布, 障碍物(插图黑色区域)介电常数2.25; (b) 电场Ez幅度的分布, 障碍物介电常数11.7; (c) 边界态沿z型路线传输Ez场的分布, 插图为局部放大的能流矢量分布; (d) 边界态沿z型路线传输的能流矢量和Ez场的分布, 和图(c)比较, 源向右移动3个晶格常数距离
Fig. 7. Robust of the topological boundary states and the pseudo-spin source position represented by white hexagonal star: (a) The distribution of the Ez field amplitude with the obstacle (the black area in the illustration) permittivity 2.25; (b) the distribution of the Ez field amplitude with the obstacle permittivity 11.7; (c) the distribution of the Ez field from the edge state transmission along the z-type route (the inset shows a locally amplified Poynting vector distribution); (d) the distribution of the Ez field and the energy flow vectors from the edge state transmission along the z-type route with the source moved 3a to the right.
表 1 电场能量密度在两种类型结构的分布
Table 1. Distribution of electric field energy density in two structures.
p orbit d orbit Type A $\begin{array}{l}\dfrac{ { { {\bar w}_{ {\rm{air} } } } } }{ { { {\bar w}_{ {\rm{dielectric} } } } } } = \dfrac{ {9.8962 \times { {10}^{ - 13} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } }{ {6.4143 \times { {10}^{ - 11} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } } = 0.01542\end{array}$ $\begin{array}{l}\dfrac{ { { {\bar w}_{ {\rm{air} } } } } }{ { { {\bar w}_{ {\rm{dielectric} } } } } } = \dfrac{ {2.834 \times { {10}^{ - 12} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } }{ {5.9366 \times { {10}^{ - 11} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } } = 0.04774\end{array}$ Type D $\begin{array}{l}\dfrac{ { { {\bar w}_{ {\rm{air} } } } } }{ { { {\bar w}_{ {\rm{dielectric} } } } } } = \dfrac{ {3.2652 \times { {10}^{ - 12} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } }{ {9.2058 \times { {10}^{ - 11} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } } = 0.03574\end{array}$ $\begin{array}{l}\dfrac{ { { {\bar w}_{ {\rm{air} } } } } }{ { { {\bar w}_{ {\rm{dielectric} } } } } } = \dfrac{ {3.603 \times { {10}^{ - 12} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } }{ {8.5597 \times { {10}^{ - 11} }\, {\rm{J} } \cdot { {\rm{m} }^{ - 2} } } } = 0.042\end{array}$ 
下载: 导出CSV
-
[1] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[2] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[3] Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[4] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
Google Scholar
[5] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[6] Sheng L, Sheng D N, Ting C S, Haldane F D M 2005 Phys. Rev. Lett. 95 136602
Google Scholar
[7] Wang Z, Chong Y D, Joannopoulos J D, et al. 2009 Nature 461 772
Google Scholar
[8] Wang Z, Chong Y D, Soljačić M 2008 Phys. Rev. Lett. 100 013905
Google Scholar
[9] Fang Y T, He H Q, Hu J X, Wen Z 2016 Phys. Rev. A 91 033827
Google Scholar
[10] Fang Y T, He H Q, Hu J X 2016 IEEE J. Sel. Top. Quant. 22 4901109
Google Scholar
[11] Lu L, Joannopoulos J D, Soljaˇci′c M 2014 Nat. Photonics 8 821
Google Scholar
[12] 孙晓晨, 何程, 卢明辉, 陈延峰 2017 66 224203
Google Scholar
Sun X C, He C, Lu M H, Chen Y F 2017 Acta Phys. Sin. 66 224203
Google Scholar
[13] 王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延峰 2019 68 224206
Google Scholar
Wang H F, Xie B Y, Zhan P, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 224206
Google Scholar
[14] Skirlo S A, Lu L, Soljačić M 2014 Phys. Rev. Lett. 113 113904
Google Scholar
[15] Khanikaev A B, Mousavi S H, Tse W K, Kargarian M, MacDonald A H, Shvets G 2013 Nat. Mater. 12 233
Google Scholar
[16] He C, Sun X C, Liu X P, Lu M H, Chen Y, Feng L, Chen Y F 2016 Proc. Natl. Acad. Sci. USA 113 4924
Google Scholar
[17] Guo Z W, Jiang H T, Long Y, Yu K, Ren J, Xue C H, Chen H 2017 Sci. Rep. 7 7742
Google Scholar
[18] Bisharat D J, Sievenpiper D F 2019 Laser Photonics Rev. 13 1900126
Google Scholar
[19] Wu L H, Hu X 2015 Phys. Rev. Lett. 114 223901
Google Scholar
[20] Li Y, Sun Y, Zhu W W, Guo Z W, Jiang J, Kariyado T, Chen H, Hu X 2018 Nat. Commun. 9 4598
Google Scholar
[21] Huang X Q, Yang Y T, Hang Z H, Zhang Z Q, Chan C T 2016 Phys. Rev. B 93 085415
Google Scholar
[22] Xu L, Wang H X, Xu Y D, Chen H Y, Jiang J H 2016 Opt. Express 24 18059
Google Scholar
[23] Mei J, Chen Z G, Wu Y 2016 Sci. Rep. 6 32752
Google Scholar
[24] Gao Y F, Jiang Z and Zhang L L, et al. 2018 J. Appl. Phys. 124 213107
Google Scholar
[25] 王键, 吴世巧, 梅军 2017 66 224301
Google Scholar
Wang J, Wu S Q, Mei J 2017 Acta Phys. Sin. 66 224301
Google Scholar
[26] 贾鼎, 葛勇, 袁寿其, 孙宏祥 2019 68 224301
Google Scholar
Jia D, Ge Y, Yuan S Q, Sun H X 2019 Acta Phys. Sin. 68 224301
Google Scholar
[27] Xia B Z, Fan H Y, Liu T T 2019 Int. J. Mech. Sci. 155 197
Google Scholar
[28] Yang Y T, Xu Y F, Xu T, Wang H X, Jiang J H, Hu X, Hang Z H 2018 Phys. Rev. Lett. 120 217401
Google Scholar
[29] Yang Y H, Sun H X, Xia J P, Xue H R, Guo Z, Ge Y, Jia D, Yuan S Q, Chong Y D, Zhang B L 2019 Nat. Phys. 15 645
Google Scholar
[30] John D J, Steven G J, Robert D M 2008 Photonic Crystals Molding the Flow of Light (2nd Ed.) (Princeton: Princeton University Press) pp46–49
[31] 温熙森, 温激鸿, 郁殿龙, 王刚, 刘耀宗, 韩小云 2009 声子晶体 (北京: 国防工业出版社) 第8页
Wen X S, Wen J H, Yu D L, Wang G, Liu Y Z, Han X Y 2009 Phononic Crystals (Beijing: National Defense Industry Press) p8 (in Chinese)
[32] Lemoult F, Kaina N, Fink M, Lerosey 2013 Nat. Phys. 9 55
Google Scholar
[33] Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757
Google Scholar
[34] Xia J P, Jia D, Sun H X, Yuan S Q, Ge Y, Si Q R, Liu X J 2018 Adv. Mater. 30 1805002
Google Scholar
[35] Jiang Z, Gao Y F, He L, Sun J P, Song H, Wang Q 2019 Phys. Chem. Chem. Phys. 21 11367
Google Scholar
[36] Ji C Y, Liu G B, Zhang Y Y, Zou B S, Yao Y G 2019 Phys. Rev. A 99 043801
Google Scholar
-
[1] 杨玉婷, 钱欣悦, 石礼伟. 二维光子晶体中赝磁场作用下的电磁波操控. , 2023, 72(13): 134203. doi: 10.7498/aps.72.20222242 [2] 刘香莲, 李凯宙, 李晓琼, 张强. 二维电介质光子晶体中量子自旋与谷霍尔效应共存的研究. , 2023, 72(7): 074205. doi: 10.7498/aps.72.20221814 [3] 隋文杰, 张玉, 张紫瑞, 王小龙, 张洪方, 史强, 杨冰. 拓扑自旋光子晶体中螺旋边界态单向传输调控研究. , 2022, 71(19): 194101. doi: 10.7498/aps.71.20220353 [4] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江. 一维 ${\cal {PT}}$ 对称非厄米自旋轨道耦合Su-Schrieffer-Heeger模型的拓扑性质. , 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796[5] 骆全斌, 黄学勤, 邓伟胤, 吴迎, 陆久阳, 刘正猷. 声子晶体板中的第二类狄拉克点和边缘传输. , 2021, 70(18): 184302. doi: 10.7498/aps.70.20210712 [6] 裴东亮, 杨洮, 陈猛, 刘宇, 徐文帅, 张满弓, 姜恒, 王育人. 基于复合蜂窝结构的宽带周期与非周期声拓扑绝缘体. , 2020, 69(2): 024302. doi: 10.7498/aps.69.20191454 [7] 郑周甫, 尹剑飞, 温激鸿, 郁殿龙. 基于声子晶体板的弹性波拓扑保护边界态. , 2020, 69(15): 156201. doi: 10.7498/aps.69.20200542 [8] 王彦兰, 李妍. 二维介电光子晶体中的赝自旋态与拓扑相变. , 2020, 69(9): 094206. doi: 10.7498/aps.69.20191962 [9] 王一鹤, 张志旺, 程营, 刘晓峻. 声子晶体中的表面声波赝自旋模式和拓扑保护声传输. , 2019, 68(22): 227805. doi: 10.7498/aps.68.20191363 [10] 杨圆, 陈帅, 李小兵. Rashba自旋轨道耦合下square-octagon晶格的拓扑相变. , 2018, 67(23): 237101. doi: 10.7498/aps.67.20180624 [11] 王青海, 李锋, 黄学勤, 陆久阳, 刘正猷. 一维颗粒声子晶体的拓扑相变及可调界面态. , 2017, 66(22): 224502. doi: 10.7498/aps.66.224502 [12] 沈清玮, 徐林, 蒋建华. 圆环结构磁光光子晶体中的拓扑相变. , 2017, 66(22): 224102. doi: 10.7498/aps.66.224102 [13] 王健, 吴世巧, 梅军. 二维声子晶体中简单旋转操作导致的拓扑相变. , 2017, 66(22): 224301. doi: 10.7498/aps.66.224301 [14] 武执政, 余坤, 郭志伟, 李云辉, 江海涛. 类特异材料半导体复合结构中的电子Tamm态. , 2015, 64(10): 107302. doi: 10.7498/aps.64.107302 [15] 张正仁, 隆正文, 袁玉群, 刁心峰. 对称型单负交替一维光子晶体的能带结构. , 2010, 59(1): 587-591. doi: 10.7498/aps.59.587 [16] 朱永政, 尹计秋, 邱明辉. 非密堆积TiO2空心微球光子晶体的制备与能带分析. , 2008, 57(12): 7725-7728. doi: 10.7498/aps.57.7725 [17] 关春颖, 苑立波. 六角蜂窝结构光子晶体异质结带隙特性研究. , 2006, 55(3): 1244-1247. doi: 10.7498/aps.55.1244 [18] 董慧媛, 刘 楣, 吴宗汉, 汪 静, 王振林. 由介质球构成的三维光子晶体能带结构的平面波研究. , 2005, 54(7): 3194-3199. doi: 10.7498/aps.54.3194 [19] 刘晓东, 王义全, 许兴胜, 程丙英, 张道中. 具有态守恒赝隙的光子晶体中两能级原子自发辐射的增强与抑制. , 2004, 53(1): 125-131. doi: 10.7498/aps.53.125 [20] 李 岩, 郑瑞生, 冯玉春, 牛憨笨. 含有理想导体的准分形结构光子晶体的能带. , 2004, 53(9): 3205-3210. doi: 10.7498/aps.53.3205
下载:
计量
- 文章访问数: 9610
- PDF下载量: 379
- 被引次数: 0
