-
二维Su-Schrieffer-Heeger(SSH)模型是在拓扑物理领域受到广泛研究的一种模型, 具有许多独特的物理性质. 它属于高阶拓扑绝缘体, 在第二条和第三条能带间会产生具有连续谱束缚态(bound states in the continuum, BICs)性质的角态. 本文首先介绍了二维SSH模型的拓扑性质, 在此基础上论证了第二条和第三条能带何时会在整个布里渊区上产生能隙. 随后, 计算了模型的电荷极化分布和电荷密度分布, 证明了当x方向上胞内跃迁几率和胞间跃迁几率较大时, x方向的边缘电荷极化激发了y方向的边缘态, 反之亦然. 同时, 边缘电荷极化激发了角上的异常填充, 产生了具有良好局域性与鲁棒性的拓扑角态. 最后, 构建了一种声学谐振腔模型, 并证明了该模型可以较好的模拟各向异性二维SSH模型的拓扑性质.
The one-dimensional (1D) Su-Schrieffer-Heeger (SSH) chain is a model that has been widely studied in the field of topological physics. The two-dimensional (2D) SSH model is a 2D extension of the 1D SSH chain and has many unique physical properties. It is a higher-order topological insulator (HOTI), in which corner states with bound states in the continuum (BIC) properties will arise between the second energy band and the third energy band. There are two different topological phases in the isotropic 2D SSH model, and a topological phase transition will happen when the intracell coupling strength is equal to the intercell coupling strength. In this paper, we first break the isotropy of the isotropic 2D SSH model, defining the ratio of the x-directional coupling strength to the y-directional coupling strength as α and the ratio of the intercell coupling strength to the intracell coupling strength as β, which represent the strength of the topological property and anisotropy respectively. We use α and β to calibrate all possible models, classify them as three different types of phases, and draw their phase diagrams.Then we argue when the energy gap between the second energy band and the third energy band emerges over the entire Brillouin zone. Meanwhile, we use a method to calculate the spatial distribution of polarization when the model is half-filled, and it is shown that there is 1/2 polarization localized at the edges in the direction with larger intracell coupling, but no edge polarization in the other direction. The edge polarization excites the edge dipole moment, giving rise to a topological edge state in the energy gap. At the same time, when the model has an entire open boundary, the dipole moment directs the charge to accumulate on the corners, which can be observed from the local charge density distribution. This type of fractional charge is a filling anomaly and formed spontaneously by the lattice to maintain electrical neutrality and rotational symmetry simultaneously. This fractional charge induces the aforementioned corner state. And by its nature of filling anomaly, this corner state is better localized and robust. It will not couple with the bulk state as long as the rotational symmetry or chirality of the model is not broken. Finally, we construct an acoustic resonant cavity model: a rectangular shaped resonant cavity is used to simulate individual lattice points and the coupling strength between the lattice points is controlled by varying the diameter of the conduit between the resonant cavities. According to the Comsol calculation results, we can see that the topological properties of the anisotropic two-dimensional SSH model are well simulated by this model. [1] Klitzing K V, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Thouless D J, Kohmoto M, Nightingale M P, Den Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[3] Ma G, Xiao M, Chan C T 2019 Nat. Rev. Phys. 1 281
Google Scholar
[4] Huber S D 2016 Nat. Phys. 12 621
Google Scholar
[5] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[6] Zhang X J, Xiao M, Cheng Y, Lu M H, Christensen J 2018 Commun. Phys. 1 97
Google Scholar
[7] Lu L, Joannopoulos J D, Soljačić M 2014 Nat. Photonics 8 821
Google Scholar
[8] Haldane F D, Raghu S 2008 Phys. Rev. Lett. 100 013904
Google Scholar
[9] Wang Z, Chong Y, Joannopoulos J D, Soljacic M 2009 Nature 461 772
Google Scholar
[10] Song Z, Fang Z, Fang C 2017 Phys. Rev. Lett. 119 246402
Google Scholar
[11] Langbehn J, Peng Y, Trifunovic L, von Oppen F, Brouwer P W 2017 Phys. Rev. Lett. 119 246401
Google Scholar
[12] Serra G M, Peri V, Susstrunk R, Bilal O R, Larsen T, Villanueva L G, Huber S D 2018 Nature 555 342
Google Scholar
[13] Peterson C W, Benalcazar W A, Hughes T L, Bahl G 2018 Nature 555 346
Google Scholar
[14] Imhof S, Berger C, Bayer F, Brehm J, Molenkamp L W, Kiessling T, Schindler F, Lee C H, Greiter M, Neupert T, Thomale R 2018 Nat. Phys. 14 925
Google Scholar
[15] Noh J, Benalcazar W A, Huang S, Collins M J, Chen K P, Hughes T L, Rechtsman M C 2018 Nat. Photonics 12 408
Google Scholar
[16] Mittal S, Orre V V, Zhu G, Gorlach M A, Poddubny A, Hafezi M 2019 Nat. Photonics 13 692
Google Scholar
[17] Chen X D, Deng W M, Shi F L, Zhao F L, Chen M, Dong J W 2019 Phys. Rev. Lett. 122 233902
Google Scholar
[18] El Hassan A, Kunst F K, Moritz A, Andler G, Bergholtz E J, Bourennane M 2019 Nat. Photonics 13 697
Google Scholar
[19] Fan H, Xia B, Tong L, Zheng S, Yu D 2019 Phys. Rev. Lett. 122 204301
Google Scholar
[20] Liu S, Gao W, Zhang Q, Ma S, Zhang L, Liu C, Xiang Y J, Cui T J, Zhang S 2019 Research 2019 8609875
Google Scholar
[21] Serra G M, Süsstrunk R, Huber S D 2019 Phys. Rev. B 99 020304
Google Scholar
[22] Xue H, Yang Y, Gao F, Chong Y, Zhang B 2019 Nat. Mater. 18 108
Google Scholar
[23] Ni X, Weiner M, Alù A, Khanikaev A B 2019 Nat. Mater. 18 113
Google Scholar
[24] Zhang X, Wang H X, Lin Z K, Tian Y, Xie B, Lu M H, Chen Y F, Jiang J H 2019 Nat. Phys. 15 582
Google Scholar
[25] Zhang Z, Long H, Liu C, Shao C, Cheng Y, Liu X, Christensen J 2019 Adv. Mater. 31 1904682
Google Scholar
[26] Zhang X, Xie B Y, Wang H F, Xu X, Tian Y, Jiang J H, Lu M H, Chen Y F 2019 Nat. Commun. 10 5331
Google Scholar
[27] Weiner M, Ni X, Li M, Alù A, Khanikaev A B 2020 Sci. Adv. 6 eaay4166
Google Scholar
[28] Qi Y, Qiu C, Xiao M, He H, Ke M, Liu Z 2020 Phys. Rev. Lett. 124 206601
Google Scholar
[29] Xie B Y, Su G X, Wang H F, Su H, Shen X P, Zhan P, Lu M H, Wang Z L, Chen Y F 2019 Phys. Rev. Lett. 122 233903
Google Scholar
[30] Coutant A, Achilleos V, Richoux O, Theocharis G, Pagneux V 2021 J. Appl. Phys. 129 125108
Google Scholar
[31] Obana D, Liu F, Wakabayashi K 2019 Phys. Rev. B 100 075437
Google Scholar
[32] Lieu S 2018 Phys. Rev. B 97 045106
Google Scholar
[33] Yuce C, Ramezani H 2019 Phys. Rev. A 100 032102
Google Scholar
[34] Dangel F, Wagner M, Cartarius H, Main J, Wunner G 2018 Phys. Rev. A 98 013628
Google Scholar
[35] Bomantara R W, Zhou L, Pan J, Gong J 2019 Phys. Rev. B 99 045441
Google Scholar
[36] Xie B Y, Wang H F, Wang H X, Zhu X Y, Jiang J H, Lu M H, Chen Y F 2018 Phys. Rev. B 98 205147
Google Scholar
[37] Zhen B, Hsu C W, Lu L, Stone A D, Soljacic M 2014 Phys. Rev. Lett. 113 257401
Google Scholar
[38] Molina M I, Miroshnichenko A E, Kivshar Y S 2012 Phys. Rev. Lett. 108 070401
Google Scholar
[39] Weimann S, Xu Y, Keil R, Miroshnichenko A E, Tunnermann A, Nolte S, Sukhorukov A A, Szameit A, Kivshar Y S 2013 Phys. Rev. Lett. 111 240403
Google Scholar
[40] Benalcazar W A, Cerjan A 2020 Phys. Rev. B 101 161116
Google Scholar
[41] Benalcazar W A, Bernevig B A, Hughes T L 2017 Phys. Rev. B 96 245115
Google Scholar
[42] Hsu C W, Zhen B, Stone A D, Joannopoulos J D, Soljačić M 2016 Nat. Rev. Mater. 1 16048
Google Scholar
[43] Stillinger F H, Herrick D R 1975 Phys. Rev. A 11 446
Google Scholar
[44] Friedrich H, Wintgen D 1985 Phys. Rev. A:Gen Phys 32 3231
Google Scholar
[45] Marinica D C, Borisov A G, Shabanov S V 2008 Phys. Rev. Lett. 100 183902
Google Scholar
[46] Shipman S P, Venakides S 2005 Phys. Rev. E:Stat. Nonlinear Soft Matter Phys. 71 026611
Google Scholar
[47] Moiseyev N 2009 Phys. Rev. Lett. 102 167404
Google Scholar
[48] Plotnik Y, Peleg O, Dreisow F, Heinrich M, Nolte S, Szameit A, Segev M 2011 Phys. Rev. Lett. 107 183901
Google Scholar
[49] Lee J, Zhen B, Chua S L, Qiu W, Joannopoulos J D, Soljacic M, Shapira O 2012 Phys. Rev. Lett. 109 067401
Google Scholar
[50] Evans D V, Levitin M, Vassiliev D 2006 J. Fluid Mech. 261 21
Google Scholar
[51] Koshelev K, Lepeshov S, Liu M, Bogdanov A, Kivshar Y 2018 Phys. Rev. Lett. 121 193903
Google Scholar
[52] Liu F, Wakabayashi K 2017 Phys. Rev. Lett. 118 076803
Google Scholar
[53] Benalcazar W A, Bernevig B A, Hughes T L 2017 Science 357 61
Google Scholar
[54] Benalcazar W A, Li T H, Hughes T L 2019 Phys. Rev. B 99 245151
Google Scholar
[55] Li C A, Wu S S 2020 Phys. Rev. B 101 195309
Google Scholar
-
图 1 (a) 二维SSH模型原胞示意图; (b) 二维SSH模型在倒空间的示意图; (c) 二维SSH模型的相图. 图中黑色, 绿色, 蓝色五角星标记了三种典型的拓扑相, 其代表的参数
$\left( {\alpha , \beta } \right)$ 分别为$\left( {1.5, 3} \right)$ ,$\left( {2, 3} \right)$ ,$\left( {2.5, 3} \right)$ ; (d) 图1(c)中黑色五角星代表的模型的带结构图, 红色圆形标记了高对称点X上第二条和第三条能带的变化过程; (e) 绿色五角星代表的模型的带结构图; (f) 蓝色五角星代表的模型的带结构图Fig. 1. (a) Schematic diagram of the original cell of the 2D SSH model; (b) schematic diagram of the 2D SSH model in inverse space; (c) phase diagram of the 2D SSH model. The black, green and blue pentagrams in the figure mark the three typical topological phases with the parameters
$\left( {\alpha , \beta } \right)$ as$\left( {1.5, 3} \right)$ ,$\left( {2, 3} \right)$ and$\left( {2.5, 3} \right)$ respectively; (d) a diagram of the band structure of the model represented by the black pentagram in Fig. 1(c), and the red circles mark the evolution process of the second and third energy bands at the high symmetry point X; (e) band structure for the model represented by the green pentagram; (f) band structure for the model represented by the blue pentagram.
图 2 电荷极化与电荷密度分布计算结果 (a) 电荷极化分布计算结果. 使用的参数为
$ \alpha = 5, \beta = 4 $ , 计算中使用了半无限大的条带模型, 开放边界的一侧计算了有20个原胞, 从左至右分别为电荷极化的x方向分量和y方向分量; (b) 拓扑平庸态下的电荷极化分布. 使用的参数为$\alpha = 5, \beta = 0.25$ ; (c) 电荷密度分布计算结果, 计算中使用了20 × 20个原胞; (d) 拓扑平庸态下的电荷极化分布Fig. 2. Calculation result of polarization and charge density distribution: (a) Calculated results of the polarization intensity distribution. The parameters used are
$\alpha = 5, \beta = 4$ , a semi-infinite strip model is used, and there are 20 primary cells on the side of the open boundary. From left to right, for the x- and y-directional components of the polarization; (b) calculated results of the polarization intensity distribution in topological trival phase. The parameters used are$\alpha = 5, \beta = 0.25$ ; (c) calculated results of the charge density distribution, 20 × 20 unit cells used in the calculation; (d) calculated results of the charge density distribution in topological trival phase.
图 3 (a) 二维SSH模型的态密度分布. 使用的参数为
$ \alpha = 5, \beta = 4 $ , 计算中使用了20 × 20个原胞; (b) x方向投影能带图, 蓝色标记部分为边缘态, 计算中使用了50个原胞; (c) y方向投影能带图; (d) 体态的局域态密度分布; (e) 边缘态的局域态密度分布; (f) 角态的局域态密度分布Fig. 3. (a) Density of states distribution for the 2D SSH model. The parameters used are
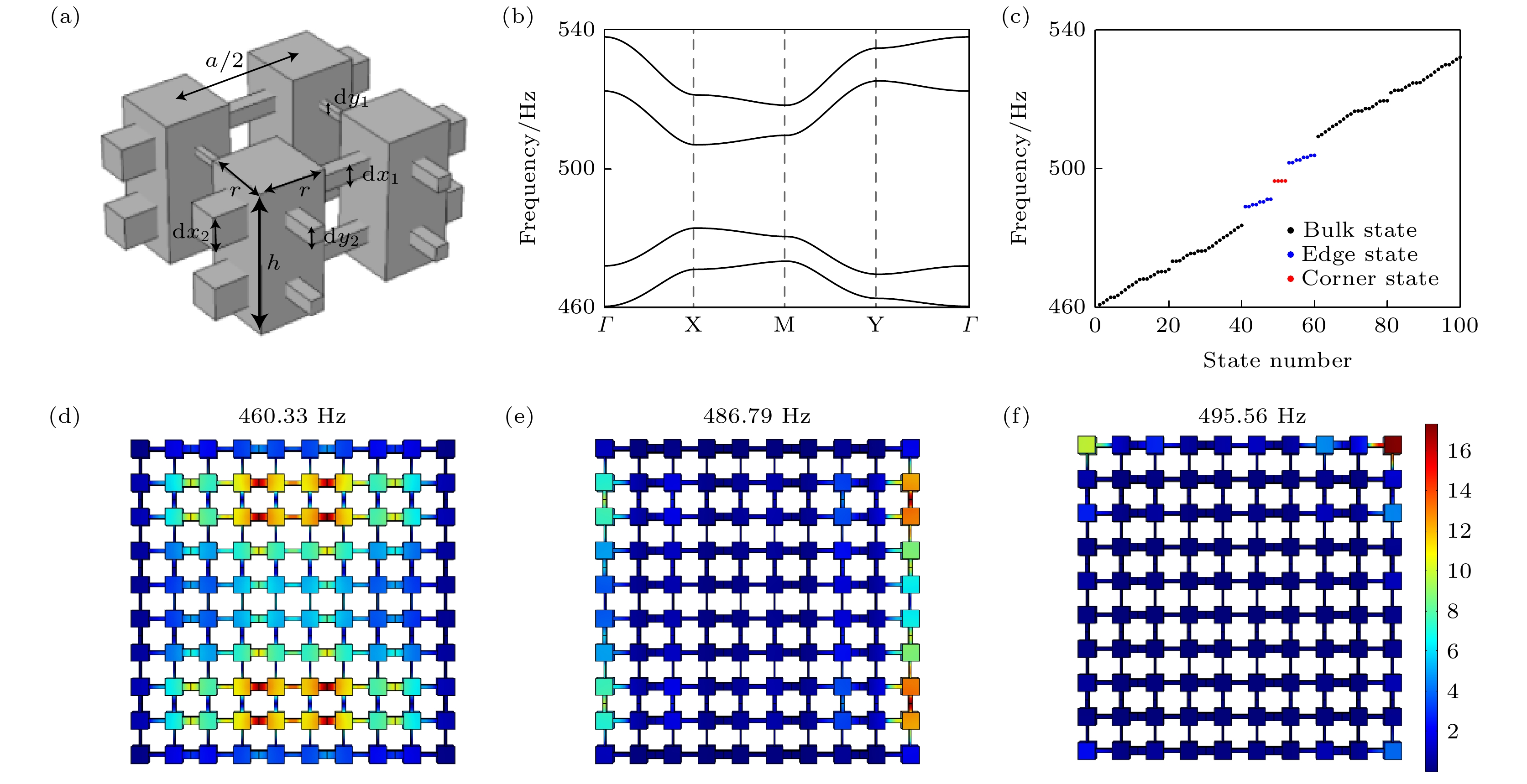
$\alpha = 5, \beta = 4$ . 20 × 20 unit cells used in the calculation; (b) projected band diagram in x-direction, with edge states marked in blue, 50 unit cells used in the calculation; (c) projected band diagram in y-direction; (d) local density distribution of bulk states; (e) local density distribution of edge states; (f) local density distribution of corner states.
图 4 (a) 计算中使用的原胞模型示意图; (b) 模拟计算的带结构图; (c) 模拟计算的态密度分布图, 计算中使用了8 × 8个原胞; (d) 体态声压场分布示意图; (e) 边缘态声压场分布示意图; (f) 角态声压场分布示意图.
Fig. 4. (a) Schematic diagram of the unit cell model used in the calculations; (b) diagram of the band structure for the simulations; (c) diagram of the density of states distribution for the simulations with 8 × 8 unit cells used; (d) schematic diagram of the bulk sound pressure field distribution; (e) schematic diagram of the edge state sound pressure field distribution; (f) schematic diagram of corner state sound pressure field distribution.
表 1 运用威尔森循环法计算二维SSH模型Zak phase的结果
Table 1. Results of the two-dimensional SSH model Zak phase using the Willson Loop method.
相 占据的能带数目 1 2 3 4 相①(左半部分) (1/2, 1/2) (0, 0) (0, 0) (1/2, 1/2) 相①(右半部分) (1/2, 1/2) (0, 0) (0, 0) (1/2, 1/2) 相② (1/2, 1/2) (0, 0) (0, 0) (1/2, 1/2) 相③ (0, 0) (0, 0) (0, 0) (0, 0) 
下载: 导出CSV
-
[1] Klitzing K V, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Thouless D J, Kohmoto M, Nightingale M P, Den Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[3] Ma G, Xiao M, Chan C T 2019 Nat. Rev. Phys. 1 281
Google Scholar
[4] Huber S D 2016 Nat. Phys. 12 621
Google Scholar
[5] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[6] Zhang X J, Xiao M, Cheng Y, Lu M H, Christensen J 2018 Commun. Phys. 1 97
Google Scholar
[7] Lu L, Joannopoulos J D, Soljačić M 2014 Nat. Photonics 8 821
Google Scholar
[8] Haldane F D, Raghu S 2008 Phys. Rev. Lett. 100 013904
Google Scholar
[9] Wang Z, Chong Y, Joannopoulos J D, Soljacic M 2009 Nature 461 772
Google Scholar
[10] Song Z, Fang Z, Fang C 2017 Phys. Rev. Lett. 119 246402
Google Scholar
[11] Langbehn J, Peng Y, Trifunovic L, von Oppen F, Brouwer P W 2017 Phys. Rev. Lett. 119 246401
Google Scholar
[12] Serra G M, Peri V, Susstrunk R, Bilal O R, Larsen T, Villanueva L G, Huber S D 2018 Nature 555 342
Google Scholar
[13] Peterson C W, Benalcazar W A, Hughes T L, Bahl G 2018 Nature 555 346
Google Scholar
[14] Imhof S, Berger C, Bayer F, Brehm J, Molenkamp L W, Kiessling T, Schindler F, Lee C H, Greiter M, Neupert T, Thomale R 2018 Nat. Phys. 14 925
Google Scholar
[15] Noh J, Benalcazar W A, Huang S, Collins M J, Chen K P, Hughes T L, Rechtsman M C 2018 Nat. Photonics 12 408
Google Scholar
[16] Mittal S, Orre V V, Zhu G, Gorlach M A, Poddubny A, Hafezi M 2019 Nat. Photonics 13 692
Google Scholar
[17] Chen X D, Deng W M, Shi F L, Zhao F L, Chen M, Dong J W 2019 Phys. Rev. Lett. 122 233902
Google Scholar
[18] El Hassan A, Kunst F K, Moritz A, Andler G, Bergholtz E J, Bourennane M 2019 Nat. Photonics 13 697
Google Scholar
[19] Fan H, Xia B, Tong L, Zheng S, Yu D 2019 Phys. Rev. Lett. 122 204301
Google Scholar
[20] Liu S, Gao W, Zhang Q, Ma S, Zhang L, Liu C, Xiang Y J, Cui T J, Zhang S 2019 Research 2019 8609875
Google Scholar
[21] Serra G M, Süsstrunk R, Huber S D 2019 Phys. Rev. B 99 020304
Google Scholar
[22] Xue H, Yang Y, Gao F, Chong Y, Zhang B 2019 Nat. Mater. 18 108
Google Scholar
[23] Ni X, Weiner M, Alù A, Khanikaev A B 2019 Nat. Mater. 18 113
Google Scholar
[24] Zhang X, Wang H X, Lin Z K, Tian Y, Xie B, Lu M H, Chen Y F, Jiang J H 2019 Nat. Phys. 15 582
Google Scholar
[25] Zhang Z, Long H, Liu C, Shao C, Cheng Y, Liu X, Christensen J 2019 Adv. Mater. 31 1904682
Google Scholar
[26] Zhang X, Xie B Y, Wang H F, Xu X, Tian Y, Jiang J H, Lu M H, Chen Y F 2019 Nat. Commun. 10 5331
Google Scholar
[27] Weiner M, Ni X, Li M, Alù A, Khanikaev A B 2020 Sci. Adv. 6 eaay4166
Google Scholar
[28] Qi Y, Qiu C, Xiao M, He H, Ke M, Liu Z 2020 Phys. Rev. Lett. 124 206601
Google Scholar
[29] Xie B Y, Su G X, Wang H F, Su H, Shen X P, Zhan P, Lu M H, Wang Z L, Chen Y F 2019 Phys. Rev. Lett. 122 233903
Google Scholar
[30] Coutant A, Achilleos V, Richoux O, Theocharis G, Pagneux V 2021 J. Appl. Phys. 129 125108
Google Scholar
[31] Obana D, Liu F, Wakabayashi K 2019 Phys. Rev. B 100 075437
Google Scholar
[32] Lieu S 2018 Phys. Rev. B 97 045106
Google Scholar
[33] Yuce C, Ramezani H 2019 Phys. Rev. A 100 032102
Google Scholar
[34] Dangel F, Wagner M, Cartarius H, Main J, Wunner G 2018 Phys. Rev. A 98 013628
Google Scholar
[35] Bomantara R W, Zhou L, Pan J, Gong J 2019 Phys. Rev. B 99 045441
Google Scholar
[36] Xie B Y, Wang H F, Wang H X, Zhu X Y, Jiang J H, Lu M H, Chen Y F 2018 Phys. Rev. B 98 205147
Google Scholar
[37] Zhen B, Hsu C W, Lu L, Stone A D, Soljacic M 2014 Phys. Rev. Lett. 113 257401
Google Scholar
[38] Molina M I, Miroshnichenko A E, Kivshar Y S 2012 Phys. Rev. Lett. 108 070401
Google Scholar
[39] Weimann S, Xu Y, Keil R, Miroshnichenko A E, Tunnermann A, Nolte S, Sukhorukov A A, Szameit A, Kivshar Y S 2013 Phys. Rev. Lett. 111 240403
Google Scholar
[40] Benalcazar W A, Cerjan A 2020 Phys. Rev. B 101 161116
Google Scholar
[41] Benalcazar W A, Bernevig B A, Hughes T L 2017 Phys. Rev. B 96 245115
Google Scholar
[42] Hsu C W, Zhen B, Stone A D, Joannopoulos J D, Soljačić M 2016 Nat. Rev. Mater. 1 16048
Google Scholar
[43] Stillinger F H, Herrick D R 1975 Phys. Rev. A 11 446
Google Scholar
[44] Friedrich H, Wintgen D 1985 Phys. Rev. A:Gen Phys 32 3231
Google Scholar
[45] Marinica D C, Borisov A G, Shabanov S V 2008 Phys. Rev. Lett. 100 183902
Google Scholar
[46] Shipman S P, Venakides S 2005 Phys. Rev. E:Stat. Nonlinear Soft Matter Phys. 71 026611
Google Scholar
[47] Moiseyev N 2009 Phys. Rev. Lett. 102 167404
Google Scholar
[48] Plotnik Y, Peleg O, Dreisow F, Heinrich M, Nolte S, Szameit A, Segev M 2011 Phys. Rev. Lett. 107 183901
Google Scholar
[49] Lee J, Zhen B, Chua S L, Qiu W, Joannopoulos J D, Soljacic M, Shapira O 2012 Phys. Rev. Lett. 109 067401
Google Scholar
[50] Evans D V, Levitin M, Vassiliev D 2006 J. Fluid Mech. 261 21
Google Scholar
[51] Koshelev K, Lepeshov S, Liu M, Bogdanov A, Kivshar Y 2018 Phys. Rev. Lett. 121 193903
Google Scholar
[52] Liu F, Wakabayashi K 2017 Phys. Rev. Lett. 118 076803
Google Scholar
[53] Benalcazar W A, Bernevig B A, Hughes T L 2017 Science 357 61
Google Scholar
[54] Benalcazar W A, Li T H, Hughes T L 2019 Phys. Rev. B 99 245151
Google Scholar
[55] Li C A, Wu S S 2020 Phys. Rev. B 101 195309
Google Scholar
-
[1] 郭刚峰, 包茜茜, 谭磊, 刘伍明. 非厄米准周期系统中的二次局域体态和局域-扩展的边缘态. , 2025, 74(1): 010301. doi: 10.7498/aps.74.20240933 [2] 刘香莲, 李凯宙, 李晓琼, 张强. 二维电介质光子晶体中量子自旋与谷霍尔效应共存的研究. , 2023, 72(7): 074205. doi: 10.7498/aps.72.20221814 [3] 徐诗琳, 胡岳芳, 袁丹文, 陈巍, 张薇. 应变调控下Tl2Ta2O7中的拓扑相变. , 2023, 72(12): 127102. doi: 10.7498/aps.72.20230043 [4] 刘畅, 王亚愚. 磁性拓扑绝缘体中的量子输运现象. , 2023, 72(17): 177301. doi: 10.7498/aps.72.20230690 [5] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江. 一维 ${\cal {PT}}$ 对称非厄米自旋轨道耦合Su-Schrieffer-Heeger模型的拓扑性质. , 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796[6] 裴东亮, 杨洮, 陈猛, 刘宇, 徐文帅, 张满弓, 姜恒, 王育人. 基于复合蜂窝结构的宽带周期与非周期声拓扑绝缘体. , 2020, 69(2): 024302. doi: 10.7498/aps.69.20191454 [7] 郑周甫, 尹剑飞, 温激鸿, 郁殿龙. 基于声子晶体板的弹性波拓扑保护边界态. , 2020, 69(15): 156201. doi: 10.7498/aps.69.20200542 [8] 王彦兰, 李妍. 二维介电光子晶体中的赝自旋态与拓扑相变. , 2020, 69(9): 094206. doi: 10.7498/aps.69.20191962 [9] 方云团, 王张鑫, 范尔盼, 李小雪, 王洪金. 基于结构反转二维光子晶体的拓扑相变及拓扑边界态的构建. , 2020, 69(18): 184101. doi: 10.7498/aps.69.20200415 [10] 杨超, 陈澍. 淬火动力学中的拓扑不变量. , 2019, 68(22): 220304. doi: 10.7498/aps.68.20191410 [11] 王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延峰. 拓扑光子学研究进展. , 2019, 68(22): 224206. doi: 10.7498/aps.68.20191437 [12] 严忠波. 高阶拓扑绝缘体和高阶拓扑超导体简介. , 2019, 68(22): 226101. doi: 10.7498/aps.68.20191101 [13] 郝宁, 胡江平. 铁基超导中拓扑量子态研究进展. , 2018, 67(20): 207101. doi: 10.7498/aps.67.20181455 [14] 喻祥敏, 谭新生, 于海峰, 于扬. 利用超导量子电路模拟拓扑量子材料. , 2018, 67(22): 220302. doi: 10.7498/aps.67.20181857 [15] 杨圆, 陈帅, 李小兵. Rashba自旋轨道耦合下square-octagon晶格的拓扑相变. , 2018, 67(23): 237101. doi: 10.7498/aps.67.20180624 [16] 龙洋, 任捷, 江海涛, 孙勇, 陈鸿. 超构材料中的光学量子自旋霍尔效应. , 2017, 66(22): 227803. doi: 10.7498/aps.66.227803 [17] 沈清玮, 徐林, 蒋建华. 圆环结构磁光光子晶体中的拓扑相变. , 2017, 66(22): 224102. doi: 10.7498/aps.66.224102 [18] 王健, 吴世巧, 梅军. 二维声子晶体中简单旋转操作导致的拓扑相变. , 2017, 66(22): 224301. doi: 10.7498/aps.66.224301 [19] 王青海, 李锋, 黄学勤, 陆久阳, 刘正猷. 一维颗粒声子晶体的拓扑相变及可调界面态. , 2017, 66(22): 224502. doi: 10.7498/aps.66.224502 [20] 冉扬强, 薛立徽, 胡嗣柱. 具有一维Coulomb型对称势Dirac方程的精确解. , 2002, 51(11): 2435-2439. doi: 10.7498/aps.51.2435
下载:
计量
- 文章访问数: 11358
- PDF下载量: 848
- 被引次数: 0
