-
In order to improve the computational efficiency of multiple-relaxation-time lattice Boltzmann model (MRT), a 12-velocity multiple-relaxation-time lattice Boltzmann model (iD3Q12 MRT model) for three-dimensional incompressible flows is proposed in this work by using an inversion method. This model has higher computational efficiency than the commonly used D3Q13 MRT model in principle. In numerical simulations, the accuracy and stability of iD3Q12 MRT model are validated by simulating different flows, including steady Poiseuille flow driven by pressure, unsteady pulsatile flow driven by periodic pressure and lid-driven cavity flow. We also compare the iD3Q12 MRT model with the 13-velocity multiple-relaxation-time lattice Boltzmann model(He-Luo D3Q13 MRT model). For the Poiseuille flow and pulsatile flow, the numerical solutions of the iD3Q12 MRT model agree well with the analytical solutions. In terms of accuracy, the iD3Q12 MRT model and He-Luo D3Q13 MRT model are used to simulate Poiseuille flow with different parameters. The global relative errors of the two models are identical. Similarly, we also simulate the pulsatile flow to calculate the global relative errors of flow fields at different times and different lattice spacing. It is found that the global relative errors of the iD3Q12 MRT model are smaller than those of the He-Luo D3Q13 MRT model, and both models have the second-order spatial accuracy. Furthermore, we also simulate the pulsatile flow by changing the lattice spacing or relaxation time when the maximal pressure drop of the channel is increased, and it is found that the global relative errors calculated by the iD3Q12 MRT model are smaller than those by the He-Luo D3Q13 MRT model in most cases, but the iD3Q12 MRT model diverges when the maximal pressure drop of the channel is large. This indicates that the iD3Q12 MRT model is more accurate than the He-Luo D3Q13 MRT model in simulating unsteady pulsatile flow, but less stable. For the lid-driven cavity flow, the results show that the numerical results of the iD3Q12 MRT model agree well with those given by Ku et al [Ku H C, Hirsh R S, Taylor T D 1987 J. Comput. Phys. 70 439]. In terms of stability, the iD3Q12 MRT model is quantitatively less stable than He-Luo D3Q13 MRT model. -
Keywords:
- 12-velocity in three dimensions /
- multiple-relaxation-time /
- lattice Boltzmann model /
- incompressible flows
[1] McNamara G R, Zanetti G 1988 Phys. Rev. Lett. 61 2332
Google Scholar
[2] Higuera F, Jimenez J 1989 Europhys. Lett. 9 663
Google Scholar
[3] Higuera F, Succi S S, Benzi R 1989 Europhys. Lett. 9 345
Google Scholar
[4] Abe T 1997 J. Comput. Phys. 131 241
Google Scholar
[5] He X Y, Luo L S 1997 Phys. Rev. E 56 6811
Google Scholar
[6] Shan X W, He X Y 1998 Phys. Rev. Lett. 80 65
Google Scholar
[7] Shan X W, Chen H D 1993 Phys. Rev. E 47 1815
Google Scholar
[8] 张良奇 2014 博士学位论文 (重庆: 重庆大学)
Zhang L Q 2014 Ph. D. Dissertation (Chongqing: Chongqing University)
[9] He X Y, Shan X W, Doolen G D 1998 Phys. Rev. E 57 R13
[10] Qi D W 1999 J. Fluid. Mech. 385 41
Google Scholar
[11] Chen S Y, Chen H D, Martínez D, Matthaeus W 1991 Phys. Rev. Lett. 67 3776
Google Scholar
[12] Chen X W, Shi B C 2005 Chin. Phys. Soc. 14 1398
Google Scholar
[13] Zhang T, Shi B C, Chai Z H 2015 64 154701
Google Scholar
Pan C X, Luo L S, Miller C T 2015 Acta Phys. Sin. 64 154701
Google Scholar
[14] Velivelli A C, Bryden K M 2006 Physica A 362 139
Google Scholar
[15] Ginzburge I 2005 Adv. Water Resour. 28 1171
Google Scholar
[16] Chai Z H, Shi B C, Guo Z L 2016 J. Sci. Comput. 69 355
Google Scholar
[17] Chai Z H, Shi B C 2008 Appl. Math. Model. 32 2050
Google Scholar
[18] Du R, Sun D K, Shi B C, Chai Z H 2019 Appl. Math. Comput. 358 80
[19] Bhatnagar J, Gross E P, Krook M K 1954 Phys. Rev. 94 511
Google Scholar
[20] Qian Y, d'Humières D, Lallemand P 1992 Europhys. Lett. 17 479
Google Scholar
[21] He X Y, Luo L S 1997 J. Stat. Phys. 88 927
Google Scholar
[22] Guo Z L, Shi B C, Wang N C 2000 J. Comput. Phys. 165 288
Google Scholar
[23] He N Z, Wang N C, Shi B C, Guo Z L 2004 Chin. Phys. Soc. 13 0040
Google Scholar
[24] Ansumali S, Karlin I V, Ottinger H C 2003 Europhys. Lett. 63 798
Google Scholar
[25] Ginzburg I, Verhaeghe F, d'Humières D 2008 Commun. Comput. Phys. 3 427
[26] Ginzburg I, Verhaeghe F, d'Humières D 2008 Commun. Comput. Phys. 3 519
[27] d'Humières D 1992 AIAA J. 159 450
[28] d'Humières D 2002 Phil. Trans. R. Soc. Lond. A 360 437
Google Scholar
[29] d'Humières D, Bouzidi M'hamed, Lallemand P 2001 Phys. Rev. E 63 066702
Google Scholar
[30] Lallemand P, Luo L S 2000 Phys. Rev. E 61 6546
Google Scholar
[31] Du R, Shi B C, Chen X W 2006 Phys. Lett. A 359 564
Google Scholar
[32] Du R, Shi B C 2009 Int. J. Mod. Phys. C 20 1023
Google Scholar
[33] Zhang W H, Shi B C, Wang Y H 2015 Comput. Math. Appl. 69 997
Google Scholar
[34] Suga K, Kuwata Y, Takashima K, Chikasue R 2015 Comput. Math. Appl. 69 518
Google Scholar
[35] Luo L S, Liao W, Chen X W, Peng Y, Zhang W 2011 Phys. Rev. E 83 056710
Google Scholar
[36] Kang S K, Hassan Y A 2013 J. Comput. Phys. 232 100
Google Scholar
[37] Peng C, Nicholas G, Guo Z L, Wang L P 2018 J. Comput. Phys. 357 16
Google Scholar
[38] Guo Z L, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[39] White F M 2005 Viscous Fluid Flow (3rd Ed.) (New York: McGraw-Hill) p135
[40] O'Brien V 1975 J. Franklin I. 300 225
Google Scholar
[41] Ku H C, Hirsh R S, Taylor T D 1987 J. Comput. Phys. 70 439
Google Scholar
-
图 1 三维泊肃叶流示意图
Figure 1. The schematic of three-dimensional Poiseuille flow.
图 2 泊肃叶流数值解与解析解的对比 (a) 泊肃叶流在
$x=1$ 截面处z取不同的值时水平速度$u_{x}$ 随y变化的函数图像; (b) 在截面$z=0$ 处y取不同的值时压力p随x变化的函数图像; 直线: 解析解; 符号: 数值解; 松弛因子$\lambda_{\nu}=1.3$ Figure 2. Comparison between numerical and analytical solutions of Poiseuille flow: (a) The variation of
$u_{x}$ with y for different locations of z at section$x=1$ for Poiseuille flow; (b) the variation of pressure with x for different locations of y at section$z=0$ for Poiseuille flow. Lines, analytical solutions; symbols, numerical results; the relaxation parameter${\lambda}_{\nu}=1.3$ .
图 3 不同的
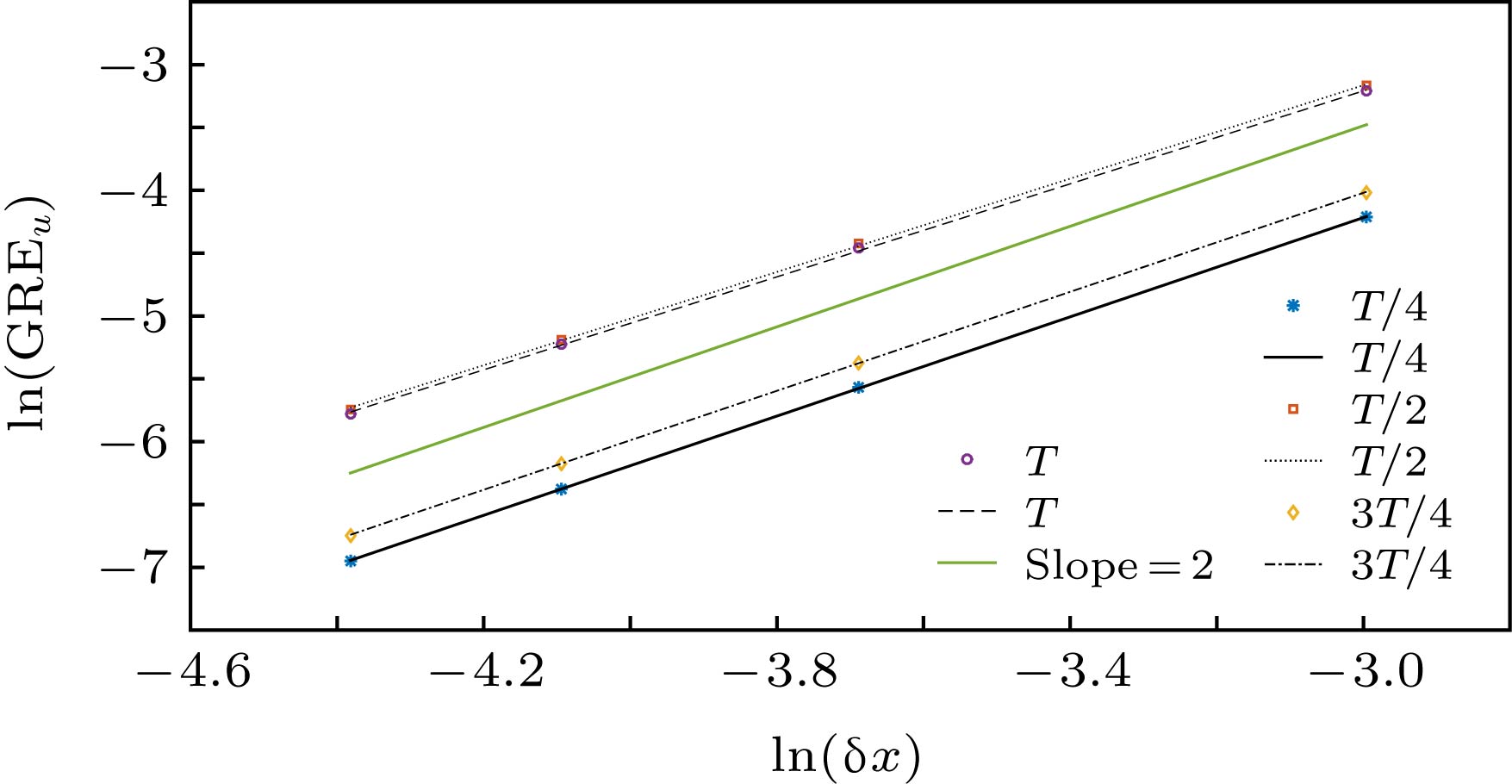
$\lambda_{\nu}$ 下, 模拟泊肃叶流得到的速度场的全局相对误差${\rm {GRE}}_u$ 随空间步长$\text{δ}{x}$ 的变化, 符号代表数值解, 连线表示拟合直线Figure 3. The variation of
${\rm {GRE}}_u$ of velocity field with the lattice spacing$\text{δ}{x}$ at different$\lambda_{\nu}$ for Poiseuille flow. Symbols represent numerical solutions, lines represent fitting line.
图 4 在
$\eta=2.8285$ 时脉动流在$x=1$ ,$z=0$ 处水平速度ux随y变化的函数. 直线: 解析解; 符号: 数值解Figure 4. The variation of horizontal velocity ux with y for pulsatile flow at the location
$x=1$ ,$z=0$ ,$\eta=2.8285$ . Line, analytical solutions; symbols, numerical solutions.
图 5 同一周期四个不同时刻下变量
${\rm {GRE}}_u$ 随空间步长$\text{δ}{x}$ 的变化Figure 5. The variation of
${\rm {GRE}}_u$ with the lattice spacing at four different times in a period for pulsatile flow.
图 6 三维顶盖驱动的方腔流示意图
Figure 6. The schematic of three-dimensional lid-driven cavity flow
图 7 不同的雷诺数下模拟方腔流, 在截面
$z=0.5$ 处竖直和水平中心线的速度分布 (a) Re = 100; (b)$Re=400$ ; (c)$Re=1000$ Figure 7. The velocity distribution in the vertical and horizontal center lines at section
$z=0.5$ for cavity flows at different$Re$ : (a)$Re=100$ ; (b)$Re=400$ ; (c)$Re=1000$ .表 1 iD3Q12 MRT和D3Q13 MRT模型在不同松弛因子
${\lambda}_{\nu}$ 和不同空间步长下计算得到的泊肃叶流的速度场的全局相对误差${\rm GRE}_u$ Table 1. The
${\rm GRE}_u$ of velocity field for Poiseuille flow computed by iD3Q12 MRT and D3Q13 MRT models under different relaxation parameters and different lattice spacings.${\rm GRE}_u$ Lattice spacing $\text{δ} x$ Model 1/8 1/16 1/32 1/64 ${\lambda}_{\nu}=0.8,$ ${\lambda}'_{\nu}=1.143$ $3.090\times10^{-2}$ $7.700\times10^{-3}$ $1.900\times10^{-3}$ $4.623\times10^{-4}$ iD3Q12 MRT $3.090\times10^{-2}$ $7.700\times10^{-3}$ $1.900\times10^{-3}$ $4.623\times10^{-4}$ D3Q13 MRT ${\lambda}_{\nu}=1.0,$ ${\lambda}'_{\nu}=1.333$ $5.990\times10^{-2}$ $1.660\times10^{-2}$ $4.400\times10^{-3}$ $1.100\times10^{-3}$ iD3Q12 MRT $5.990\times10^{-2}$ $1.660\times10^{-2}$ $4.400\times10^{-3}$ $1.100\times10^{-3}$ D3Q13 MRT ${\lambda}_{\nu}=1.3,$ ${\lambda}'_{\nu}=1.576$ $8.720\times10^{-2}$ $2.500\times10^{-2}$ $6.700\times10^{-3}$ $1.700\times10^{-3}$ iD3Q12 MRT $8.720\times10^{-2}$ $2.500\times10^{-2}$ $6.700\times10^{-3}$ $1.700\times10^{-3}$ D3Q13 MRT 
DownLoad: CSV
表 2 在
$\eta=2.8285$ 时, 不同空间步长下用iD3Q12 MRT模型和D3Q13 MRT模型模拟脉动流所得的不同时刻下的速度场的全局相对误差${\rm GRE}_u$ Table 2. The global relative errors of the velocity field at different times for pulsatile flow simulated by iD3Q12 MRT and D3Q13 MRT models at different lattice spacings,
$\eta=2.8285$ .Lattice spacing ${\rm GRE}_u$ Model $T/4$ $T/2$ $3 T/4$ T ${\rm{\text{δ}} } x= {1}/{20}$ $1.483\times10^{-2}$ $4.214\times10^{-2}$ $1.805\times10^{-2}$ $4.028\times10^{-2}$ iD3Q12 MRT $1.662\times10^{-2}$ $4.733\times10^{-2}$ $2.118\times10^{-2}$ $4.299\times10^{-2}$ D3Q13 MRT ${\rm{\text{δ}} } x= {1}/{40}$ $3.803\times10^{-3}$ $1.199\times10^{-2}$ $4.651\times10^{-3}$ $1.153\times10^{-2}$ iD3Q12 MRT $4.172\times10^{-3}$ $1.324\times10^{-2}$ $5.398\times10^{-3}$ $1.217\times10^{-2}$ D3Q13 MRT ${\rm{\text{δ}} } x= {1}/{60}$ $1.702\times10^{-3}$ $5.569\times10^{-3}$ $2.085\times10^{-3}$ $5.369\times10^{-3}$ iD3Q12 MRT $1.855\times10^{-3}$ $6.116\times10^{-3}$ $2.412\times10^{-3}$ $5.648\times10^{-3}$ D3Q13 MRT ${\rm{\text{δ}} } x= {1}/{80}$ $9.605\times10^{-4}$ $3.204\times10^{-3}$ $1.177\times10^{-3}$ $3.092\times10^{-3}$ iD3Q12 MRT $1.043\times10^{-3}$ $3.509\times10^{-3}$ $1.360\times10^{-3}$ $3.247\times10^{-3}$ D3Q13 MRT
DownLoad: CSV
表 3 相邻空间步长下的iD3Q12 MRT和D3Q13 MRT模型的空间精度的阶
Table 3. The orders of the spatial accuracy of iD3Q12 MRT and D3Q13 MRT models under adjacent spacings.
Adjacent spacing Order Model $T/4$ $T/2$ $3 T/4$ T Average 1.978 1.875 1.974 1.869 iD3Q12 MRT 1.998 1.891 1.984 1.879 D3Q13 MRT ${1}/{20} \to {1}/{40}$ 1.963 1.813 1.956 1.805 iD3Q12 MRT 1.994 1.838 1.972 1.821 D3Q13 MRT ${1}/{40}\to {1}/{60}$ 1.983 1.891 1.979 1.885 iD3Q12 MRT 1.999 1.905 1.987 1.893 D3Q13 MRT ${1}/{60} \to {1}/{80}$ 1.989 1.922 1.988 1.918 iD3Q12 MRT 2.001 1.931 1.992 1.924 D3Q13 MRT
DownLoad: CSV
表 4 在
$\tau=0.5667$ ,$\eta=4.3416$ , 最大压差$\Delta{p}$ 增大时不同的空间步长下由iD3Q12 MRT和D3Q13 MRT模型模拟的脉动流在时刻T下的速度场所计算的全局相对误差${\rm GRE}_u$ , 空白处表示计算发散Table 4. The global relative error calculated by the velocity field at time T of pulsatile flow simulated by the iD3Q12 MRT and D3Q13 MRT models under different lattice spacings. The maximal pressure drop
$ \Delta{p} $ of the channel increases,$\tau=0.5567$ ,$\eta=4.3416$ are fixed. The blank indicates that the computation is divergent.$ \Delta p $ Lattice spacing ${\rm{\text{δ}} } x$ Model 1/20 1/40 1/60 1/80 $0.005 $ $9.919\times10^{-2}$ $3.030\times10^{-2}$ $1.442\times10^{-2}$ $8.402\times10^{-3}$ iD3Q12 MRT $1.121\times10^{-1}$ $3.326\times10^{-2}$ $1.568\times10^{-2}$ $9.084\times10^{-3}$ D3Q13 MRT $0.010$ $1.172\times10^{-1}$ $3.445\times10^{-2}$ $1.618\times10^{-2}$ $9.362\times10^{-3}$ iD3Q12 MRT $1.679\times10^{-1}$ $4.763\times10^{-2}$ $2.199\times10^{-2}$ $1.260\times10^{-2}$ D3Q13 MRT $0.020$ $1.777\times10^{-1}$ $5.110\times10^{-2}$ $2.365\times10^{-2}$ $1.355\times10^{-2}$ iD3Q12 MRT $2.940\times10^{-1}$ $8.630\times10^{-2}$ $3.987\times10^{-2}$ $2.279\times10^{-2}$ D3Q13 MRT $0.050$ $1.243\times10^{-1}$ $5.848\times10^{-2}$ $3.386\times10^{-2}$ iD3Q12 MRT $2.025\times10^{-1}$ $9.868\times10^{-2}$ $5.757\times10^{-2}$ D3Q13 MRT $0.080$ $6.073\times10^{-2}$ iD3Q12 MRT $1.575\times10^{-2}$ $9.405\times10^{-2}$ D3Q13 MRT $0.100$ iD3Q12 MRT $1.192\times10^{-1}$ D3Q13 MRT $0.120$ iD3Q12 MRT $1.454\times10^{-1}$ D3Q13 MRT
DownLoad: CSV
表 5 在
${\rm{\text{δ}}} {x}={1}/{20}$ 时, 最大压差$\Delta{p}$ 增大时不同的松弛时间τ下由iD3Q12 MRT和D3Q13 MRT模型模拟的脉动流由T时刻的速度场计算得出的全局相对误差${\rm GRE}_u$ , 空白处表示计算发散Table 5. The global relative error of the velocity field at time T of the pulsatile flow simulated by the iD3Q12 MRT and D3Q13 MRT models under different relaxation time τ. The maximal pressure drop of the channel is increased and
${\rm{\text{δ}}}{x}={1}/{20}$ is fixed. The blank indicates that the computation is divergent.$\Delta p$ τ Model 0.55 0.60 0.70 0.90 $0.005 $ $1.302\times10^{-1}$ $6.311\times10^{-2}$ $2.955\times10^{-2}$ $1.744\times10^{-2}$ iD3Q12 MRT $1.556\times10^{-1}$ $6.560\times10^{-3}$ $3.023\times10^{-2}$ $1.993\times10^{-2}$ D3Q13 MRT $0.010$ $1.612\times10^{-1}$ $6.830\times10^{-2}$ $2.711\times10^{-2}$ $1.736\times10^{-2}$ iD3Q12 MRT $2.435\times10^{-1}$ $8.735\times10^{-2}$ $2.661\times10^{-2}$ $2.058\times10^{-2}$ D3Q13 MRT $0.020$ $2.475\times10^{-1}$ $9.926\times10^{-2}$ $2.624\times10^{-2}$ $1.656\times10^{-2}$ iD3Q12 MRT $4.182\times10^{-1}$ $1.542\times10^{-1}$ $2.757\times10^{-2}$ $2.195\times10^{-2}$ D3Q13 MRT $0.030$ $1.430\times10^{-1}$ $3.421\times10^{-2}$ $1.509\times10^{-2}$ iD3Q12 MRT $5.482\times10^{-1}$ $2.193\times10^{-1}$ $3.616\times10^{-2}$ $2.343\times10^{-2}$ D3Q13 MRT $0.040$ $5.001\times10^{-2}$ $1.349\times10^{-2}$ iD3Q12 MRT $4.693\times10^{-2}$ $2.502\times10^{-2}$ D3Q13 MRT $0.050$ $1.291\times10^{-2}$ iD3Q12 MRT $2.674\times10^{-2}$ D3Q13 MRT
DownLoad: CSV
表 6 不断增大雷诺数比较iD3Q12 MRT和He-Luo D3Q13 MRT模型在模拟方腔流时的稳定性.
$\checkmark$ 代表收敛, 收敛准则是(39)式Table 6. Comparing the stability of iD3Q12 MRT and He-Luo D3Q13 MRT models for three-dimensional cavity flows when the Reynolds number is continuously increased. The tick represents convergence, the convergence criterion is formula (39).
Re Model iD3Q12 MRT He-Luo D3Q13 MRT 100 $\checkmark$ $\checkmark$ 400 $\checkmark$ $\checkmark$ 1000 $\checkmark$ $\checkmark$ 1500 $\checkmark$ $\checkmark$ 1600 $\checkmark$ $\checkmark$ 1700 divergent $\checkmark$ 1800 divergent divergent
DownLoad: CSV
-
[1] McNamara G R, Zanetti G 1988 Phys. Rev. Lett. 61 2332
Google Scholar
[2] Higuera F, Jimenez J 1989 Europhys. Lett. 9 663
Google Scholar
[3] Higuera F, Succi S S, Benzi R 1989 Europhys. Lett. 9 345
Google Scholar
[4] Abe T 1997 J. Comput. Phys. 131 241
Google Scholar
[5] He X Y, Luo L S 1997 Phys. Rev. E 56 6811
Google Scholar
[6] Shan X W, He X Y 1998 Phys. Rev. Lett. 80 65
Google Scholar
[7] Shan X W, Chen H D 1993 Phys. Rev. E 47 1815
Google Scholar
[8] 张良奇 2014 博士学位论文 (重庆: 重庆大学)
Zhang L Q 2014 Ph. D. Dissertation (Chongqing: Chongqing University)
[9] He X Y, Shan X W, Doolen G D 1998 Phys. Rev. E 57 R13
[10] Qi D W 1999 J. Fluid. Mech. 385 41
Google Scholar
[11] Chen S Y, Chen H D, Martínez D, Matthaeus W 1991 Phys. Rev. Lett. 67 3776
Google Scholar
[12] Chen X W, Shi B C 2005 Chin. Phys. Soc. 14 1398
Google Scholar
[13] Zhang T, Shi B C, Chai Z H 2015 64 154701
Google Scholar
Pan C X, Luo L S, Miller C T 2015 Acta Phys. Sin. 64 154701
Google Scholar
[14] Velivelli A C, Bryden K M 2006 Physica A 362 139
Google Scholar
[15] Ginzburge I 2005 Adv. Water Resour. 28 1171
Google Scholar
[16] Chai Z H, Shi B C, Guo Z L 2016 J. Sci. Comput. 69 355
Google Scholar
[17] Chai Z H, Shi B C 2008 Appl. Math. Model. 32 2050
Google Scholar
[18] Du R, Sun D K, Shi B C, Chai Z H 2019 Appl. Math. Comput. 358 80
[19] Bhatnagar J, Gross E P, Krook M K 1954 Phys. Rev. 94 511
Google Scholar
[20] Qian Y, d'Humières D, Lallemand P 1992 Europhys. Lett. 17 479
Google Scholar
[21] He X Y, Luo L S 1997 J. Stat. Phys. 88 927
Google Scholar
[22] Guo Z L, Shi B C, Wang N C 2000 J. Comput. Phys. 165 288
Google Scholar
[23] He N Z, Wang N C, Shi B C, Guo Z L 2004 Chin. Phys. Soc. 13 0040
Google Scholar
[24] Ansumali S, Karlin I V, Ottinger H C 2003 Europhys. Lett. 63 798
Google Scholar
[25] Ginzburg I, Verhaeghe F, d'Humières D 2008 Commun. Comput. Phys. 3 427
[26] Ginzburg I, Verhaeghe F, d'Humières D 2008 Commun. Comput. Phys. 3 519
[27] d'Humières D 1992 AIAA J. 159 450
[28] d'Humières D 2002 Phil. Trans. R. Soc. Lond. A 360 437
Google Scholar
[29] d'Humières D, Bouzidi M'hamed, Lallemand P 2001 Phys. Rev. E 63 066702
Google Scholar
[30] Lallemand P, Luo L S 2000 Phys. Rev. E 61 6546
Google Scholar
[31] Du R, Shi B C, Chen X W 2006 Phys. Lett. A 359 564
Google Scholar
[32] Du R, Shi B C 2009 Int. J. Mod. Phys. C 20 1023
Google Scholar
[33] Zhang W H, Shi B C, Wang Y H 2015 Comput. Math. Appl. 69 997
Google Scholar
[34] Suga K, Kuwata Y, Takashima K, Chikasue R 2015 Comput. Math. Appl. 69 518
Google Scholar
[35] Luo L S, Liao W, Chen X W, Peng Y, Zhang W 2011 Phys. Rev. E 83 056710
Google Scholar
[36] Kang S K, Hassan Y A 2013 J. Comput. Phys. 232 100
Google Scholar
[37] Peng C, Nicholas G, Guo Z L, Wang L P 2018 J. Comput. Phys. 357 16
Google Scholar
[38] Guo Z L, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[39] White F M 2005 Viscous Fluid Flow (3rd Ed.) (New York: McGraw-Hill) p135
[40] O'Brien V 1975 J. Franklin I. 300 225
Google Scholar
[41] Ku H C, Hirsh R S, Taylor T D 1987 J. Comput. Phys. 70 439
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 9283
- PDF Downloads: 95
- Cited By: 0
