-
Ostwald熟化(ripening)是指局部热力学平衡状态下, 颗粒/液滴/气泡系统为了减小界面能而自发地进行颗粒群尺度分布调整的过程, 具有重要研究价值. 针对目前数值模拟研究不充分的现状, 本文采用格子Boltzmann方法, 对相变速率主控的二维蒸气泡系统演化开展了数值模拟研究. 模拟结果与本文推导的二维气泡群演化标度律符合较好, 证实了格子Boltzmann方法对复杂相变-物质输运过程捕捉的准确性. 研究同时表明, 蒸气泡系统演化过程中物质输运为液相压力不平衡所驱动, 并且在小气泡“溃灭”过程中水动力学作用会影响气泡群半径分布函数的局部细节; 气-液状态方程参数对熟化过程的影响效果分析显示, 气液两相比内能差是驱动相变的核心要素, 此差异越大相变速率越快, 该结论进一步诠释了化学势驱动熟化过程的物理图像.
-
关键词:
- Ostwald熟化 /
- 格子Boltzmann方法 /
- 相变 /
- Lifshitz-Slyozov-Wagner理论
Ostwald ripening refers to a process of a particle/droplet/bubble system under local thermal equilibrium state adjusting the size distribution spontaneously to reduce the total surface energy. A lattice Boltzmann approach is used to simulate the ripening process of a two dimensional vapor bubble cluster dominated by phase transition kinetics. By comparing the numerical results with the theoretical prediction derived in two-dimensional space, it is shown that the lattice Boltzmann method is accurate in the simulations. The results also indicate that the mass transfer in liquid phase is driven by hydrodynamic pressure distribution and the hydrodynamic collapse of the bubbles influences the size distribution function in a small size region. The influence of the parameters in the equation of state of the material is studied further. A positive relation between phase transition speed and specific internal energy is proposed, which enhances the thermal fundamental of phase transition.-
Keywords:
- Ostwald ripening /
- lattice Boltzmann method /
- phase transition /
- Lifshitz-Slyozov-Wagner theory
[1] Wagner Voorhees P 1985 J. Stat. Phys. 38 231
[2] Bray A J 1994 Adv. Phys. 43 357
Google Scholar
[3] Bender H, Ratke L 1998 Acta Mater. 46 1125
Google Scholar
[4] Alkemper J, Snyder V A, Akaiwa N, et al. 1999 Phys. Rev. Lett. 82 2725
Google Scholar
[5] Diddens C, Tan H, Lv P, et al. 2017 J. Fluid Mech. 823 470
Google Scholar
[6] Li Y, Garing C, Benson S M 2020 J. Fluid Mech. 889 889
[7] Ardell A J 1990 Phys. Rev. B 41 2554
Google Scholar
[8] Voorhees P W, Glicksman M E 1984 Acta Metall. 32 2001
Google Scholar
[9] Fan D, Chen L, Chen S, Voorhees P W 1998 Comput. Mater. Sci. 9 329
Google Scholar
[10] Li J, Guo C, Ma Y, Wang Z, Wang J 2015 Acta Mater. 90 10
Google Scholar
[11] Wang Y, Li J, Zhang L, Wang Z, Wang J 2020 Model. Simul. Mater. Sci. Eng. 28 075007
Google Scholar
[12] Moats K A, Asadi E, Laradji M 2019 Phys. Rev. E 99 012803
Google Scholar
[13] Watanabe H, Suzuki M, Inaoka H, Ito N 2014 J. Chem. Phys. 141 234703
Google Scholar
[14] Watanabe H, Inaoka H, Ito N 2016 J. Chem. Phys. 145 124707
Google Scholar
[15] Aidun C K, Clausen J R 2010 Annu. Rev. Fluid Mech. 42 437
[16] Guo Z, Shu C 2013 Lattice Boltzmann Method and Its Applications in Engineering (Beijing: World Scientific) pp4117–4134
[17] Shan X, Chen H 1993 Phys. Rev. E 47 1815
Google Scholar
[18] Yuan P, Schaefer L 2006 Phys. Fluids 18 042101
Google Scholar
[19] Huang H, Krafczyk M, Lu X 2011 Phys. Rev. E 84 046710
Google Scholar
[20] Chen X, Zhong C, Yuan X 2011 Comput. Math. Appl. 61 3577
Google Scholar
[21] Shi Y, Luo K, Chen X, Li D 2020 J. Hydro. Ser. B 32 845
Google Scholar
[22] Shan M, Zhu C, Yao C, Cheng Y, Jiang X 2016 Chin. Phys. B 25 104701
Google Scholar
[23] Yang Y, Shan M, Han Q, Kan X 2021 Chin. Phys. B 30 024701
Google Scholar
[24] Li Q, Kang Q J, Francois M M 2015 Int. J. Heat Mass Transfer 85 787
Google Scholar
[25] Shen L Y, Tang G H, Li Q, Shi Y 2019 Langmuir 35 9430
Google Scholar
[26] Chang X, Huang, H, Cheng Y, Lu X 2019 Int. J. Heat Mass Transfer 139 588
Google Scholar
[27] Liu M, Chen X 2017 Phys. Fluids 29 082102
Google Scholar
[28] Lifshitz I M, Slyozov V V 1961 J. Phys. Chem. Solids 19 35
[29] Chai Z, Sun D, Wang H and Shi B 2018 Int. J. Heat Mass Transfer 122 631
Google Scholar
[30] Carter A H 2007 Classical and Statistical Thermodynamics (Beijing: Tshinghua University Press) pp19–34
[31] 波林 B E, 普劳斯尼茨 J M, 奥康奈尔 J P著 (赵红玲, 王凤坤, 陈圣坤 译) 2001 汽液物性估算手册 (北京: 化学工业出版社) 第493页
Poling B E, Prausnitz J M, O’Connell (translated by Zhao H L, Wang F K, Chen S K) 2001 The Properties of Gases and Liquids (Beijing: Chemical Industry Publishing House) p493 (in Chinese)
[32] Anderson J 1995 Computational Fluid Dynamics (Berlin: McGraw-Hill Education) pp87–104
-
图 1 双气泡熟化过程气泡演化 (a) 双气泡熟化过程相分部演化; (b) 大、小气泡半径 (
$ R_2, R_1 $ )演化,$T=0.80 T_{\rm{c}}, d=500$ ; (c) 双气泡熟化过程中气相区总面积 ($ S $ )变化. 图(b)和图(c)中的红色曲线为滤波结果. 对应相变速率系数$k_{\rm{s}}=0.6845$ Fig. 1. Ostwald ripening for two bubbles: (a) Evolution of the two bubbles; (b) relation of
$ R_1, R_2\sim t $ at$T=0.80 T_{\rm{c}},\; d=500$ ; (c) evolution of the total vapor phase area ($ S $ ). The red curves are filted results in pannels (a) and (b). Corresponding$k_{\rm{s}}=0.6845$ .
图 2 双气泡熟化过程中密度、压力分布变化 (a) 双气泡中心连线上的密度分布及演化, 箭头标记了压力测点位置; (b) 图(a)中测点压力随时间的演化过程, 空心圈表示数值模拟结果, 曲线表示压力数据的平滑结果. 图标“SB”, “LB”分别表示小气泡和大气泡
Fig. 2. The pressure distribution in bubble and liquid phase during ripening: (a) Pressure distribution at different time, with the arrows marking the detected point in pannel (b); (b) temporal pressure on the four marked points. The open symbols denote the simulated results and the curves the smoothed results. Labels “SB” and “LB” denote large and small bubble, respectively
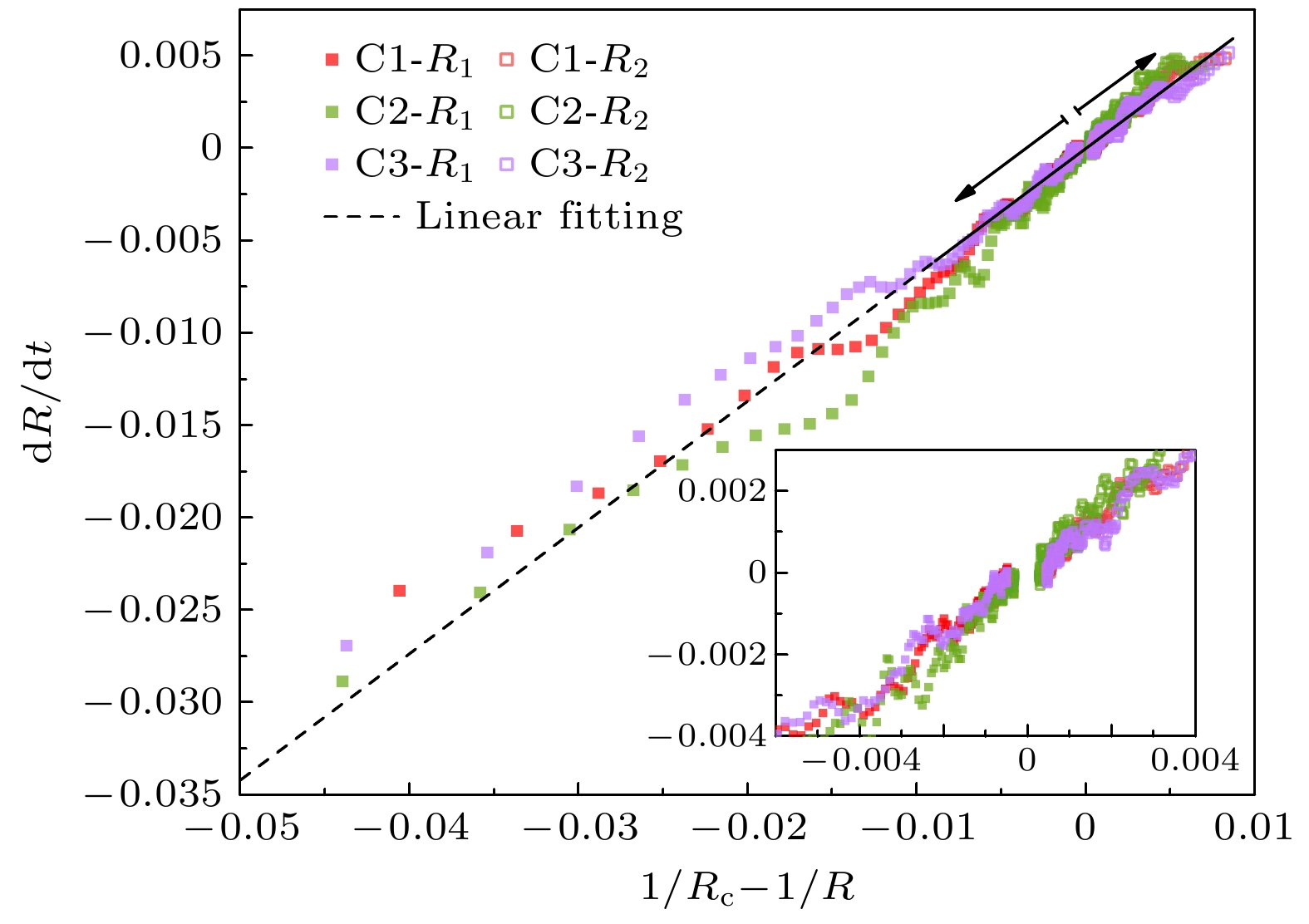
图 3 双气泡增长速率与相变驱动作用的关系, 实心点表示小气泡, 空心点表示大气泡演化过程. “C1, C2, C3” 数据分别对应计算条件(
$ R_1/R_2/d $ ) =$(57/60/500), (57/63/500), $ $ (57/60/1000)$ . 线性拟合数据点(虚线)得到$ k_{\rm{s}}=0.6845 $ . 图中箭头表示熟化过程发展方向Fig. 3. The relation of
$ {{\rm{d}}} R/ {{\rm{d}}} t\sim(1/R_{\rm{c}}-1/R) $ . The closed symbols represent small bubble evolution, and the open ones the large bubble. “C1, C2” and “C3” correspond to the cases ($ R_1/R_2/d $ ) =$(57/60/500), (57/63/500), (57/60/ $ $ 1000)$ , respectively. A linear fitting shows the slope of$ k_{\rm{s}}=0.6845 $ , and the arrows show the directions of the ripening processes for large and small bubbles, respectively
图 4
$ k_{\rm{s}} $ 对热力学参数的依赖关系 (a)不同温度和表面张力下的气泡增长速率, 其中实心点表示$ (a=1, b=4) $ 条件结果, 空心点表示表示其他$ (a, b) $ 对结果 ($a=1.0, 1.05, $ $ b=3.75—4.0$ ); (b)$ W\text{-}k_{\rm{s}} $ 关系, 其中$ W $ 表示介质相变所做的机械功Fig. 4. Variation of
$ k_{\rm{s}} $ depending on the thermal parameters in ripening process of dual bubble: (a) The$T\text{-}k_{\rm{s}}$ and$\sigma\text{-}k_{\rm{s }}$ relations. The close symbols correspond to$(a=1, $ $ b=4)$ , and the opens for various$(a, b)=(1.0-1.05, 3.75- $ $ 4.0)$ . (b) The$W\text{-}k_{\rm{s}}$ relation, where$ W $ denotes mechanical work done in phase transition
图 5 气泡群熟化过程计算结果 (a)
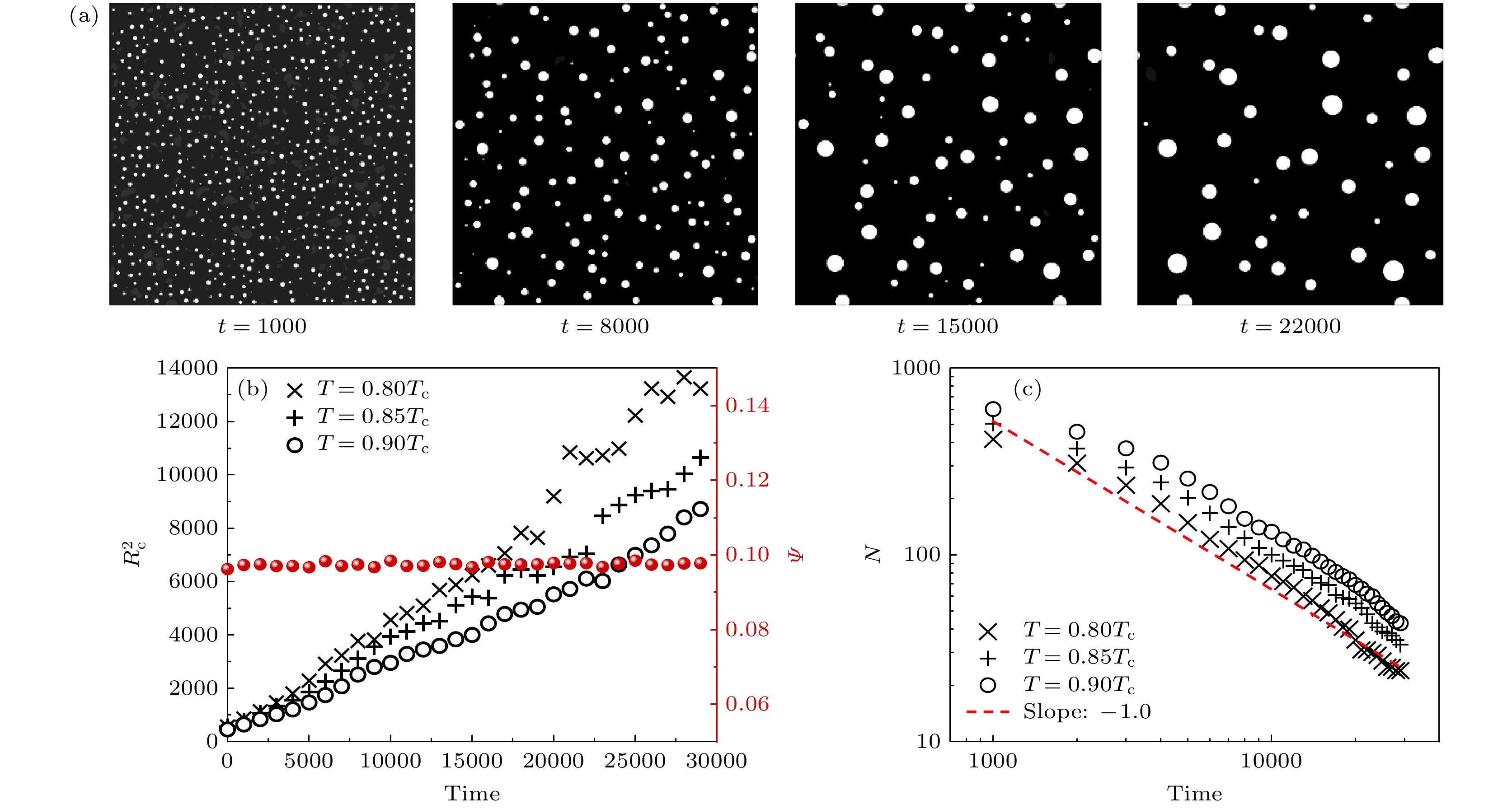
$ T=0.80 T_{\rm{c}} $ 气泡群熟化过程; (b) 气相面积演化 ($ T=0.80 T_{\rm{c}} $ )和不同温度条件下气泡群临界半径增长趋势,$ \psi $ 全场气相面积占比; (c) 不同温度条件下计算域内气泡数量演化过程. 图中斜线显示了$ N\sim t^{-1} $ 标度律Fig. 5. The simulated ripening process for vapor bubble cluster: (a) Bubble distribution in the ripening process as
$ T=0.8 T_{\rm{c }}$ ; (b) vapor area ratio ($ \psi $ ) evolution ($ T=0.8 T_{\rm{c}} $ ) and$R_{\rm{c}}^2\text{-} t$ relations for different temperatures; (c) bubble number evolutions for different temperatures. The dashed line indicates the$ N\sim t^{-1} $ scaling
图 6 气泡半径分布函数演化结果
Fig. 6. The evolution of
$ {\cal{F}}-R $ relation in ripening process -
[1] Wagner Voorhees P 1985 J. Stat. Phys. 38 231
[2] Bray A J 1994 Adv. Phys. 43 357
Google Scholar
[3] Bender H, Ratke L 1998 Acta Mater. 46 1125
Google Scholar
[4] Alkemper J, Snyder V A, Akaiwa N, et al. 1999 Phys. Rev. Lett. 82 2725
Google Scholar
[5] Diddens C, Tan H, Lv P, et al. 2017 J. Fluid Mech. 823 470
Google Scholar
[6] Li Y, Garing C, Benson S M 2020 J. Fluid Mech. 889 889
[7] Ardell A J 1990 Phys. Rev. B 41 2554
Google Scholar
[8] Voorhees P W, Glicksman M E 1984 Acta Metall. 32 2001
Google Scholar
[9] Fan D, Chen L, Chen S, Voorhees P W 1998 Comput. Mater. Sci. 9 329
Google Scholar
[10] Li J, Guo C, Ma Y, Wang Z, Wang J 2015 Acta Mater. 90 10
Google Scholar
[11] Wang Y, Li J, Zhang L, Wang Z, Wang J 2020 Model. Simul. Mater. Sci. Eng. 28 075007
Google Scholar
[12] Moats K A, Asadi E, Laradji M 2019 Phys. Rev. E 99 012803
Google Scholar
[13] Watanabe H, Suzuki M, Inaoka H, Ito N 2014 J. Chem. Phys. 141 234703
Google Scholar
[14] Watanabe H, Inaoka H, Ito N 2016 J. Chem. Phys. 145 124707
Google Scholar
[15] Aidun C K, Clausen J R 2010 Annu. Rev. Fluid Mech. 42 437
[16] Guo Z, Shu C 2013 Lattice Boltzmann Method and Its Applications in Engineering (Beijing: World Scientific) pp4117–4134
[17] Shan X, Chen H 1993 Phys. Rev. E 47 1815
Google Scholar
[18] Yuan P, Schaefer L 2006 Phys. Fluids 18 042101
Google Scholar
[19] Huang H, Krafczyk M, Lu X 2011 Phys. Rev. E 84 046710
Google Scholar
[20] Chen X, Zhong C, Yuan X 2011 Comput. Math. Appl. 61 3577
Google Scholar
[21] Shi Y, Luo K, Chen X, Li D 2020 J. Hydro. Ser. B 32 845
Google Scholar
[22] Shan M, Zhu C, Yao C, Cheng Y, Jiang X 2016 Chin. Phys. B 25 104701
Google Scholar
[23] Yang Y, Shan M, Han Q, Kan X 2021 Chin. Phys. B 30 024701
Google Scholar
[24] Li Q, Kang Q J, Francois M M 2015 Int. J. Heat Mass Transfer 85 787
Google Scholar
[25] Shen L Y, Tang G H, Li Q, Shi Y 2019 Langmuir 35 9430
Google Scholar
[26] Chang X, Huang, H, Cheng Y, Lu X 2019 Int. J. Heat Mass Transfer 139 588
Google Scholar
[27] Liu M, Chen X 2017 Phys. Fluids 29 082102
Google Scholar
[28] Lifshitz I M, Slyozov V V 1961 J. Phys. Chem. Solids 19 35
[29] Chai Z, Sun D, Wang H and Shi B 2018 Int. J. Heat Mass Transfer 122 631
Google Scholar
[30] Carter A H 2007 Classical and Statistical Thermodynamics (Beijing: Tshinghua University Press) pp19–34
[31] 波林 B E, 普劳斯尼茨 J M, 奥康奈尔 J P著 (赵红玲, 王凤坤, 陈圣坤 译) 2001 汽液物性估算手册 (北京: 化学工业出版社) 第493页
Poling B E, Prausnitz J M, O’Connell (translated by Zhao H L, Wang F K, Chen S K) 2001 The Properties of Gases and Liquids (Beijing: Chemical Industry Publishing House) p493 (in Chinese)
[32] Anderson J 1995 Computational Fluid Dynamics (Berlin: McGraw-Hill Education) pp87–104
下载:
计量
- 文章访问数: 3495
- PDF下载量: 68
- 被引次数: 0
