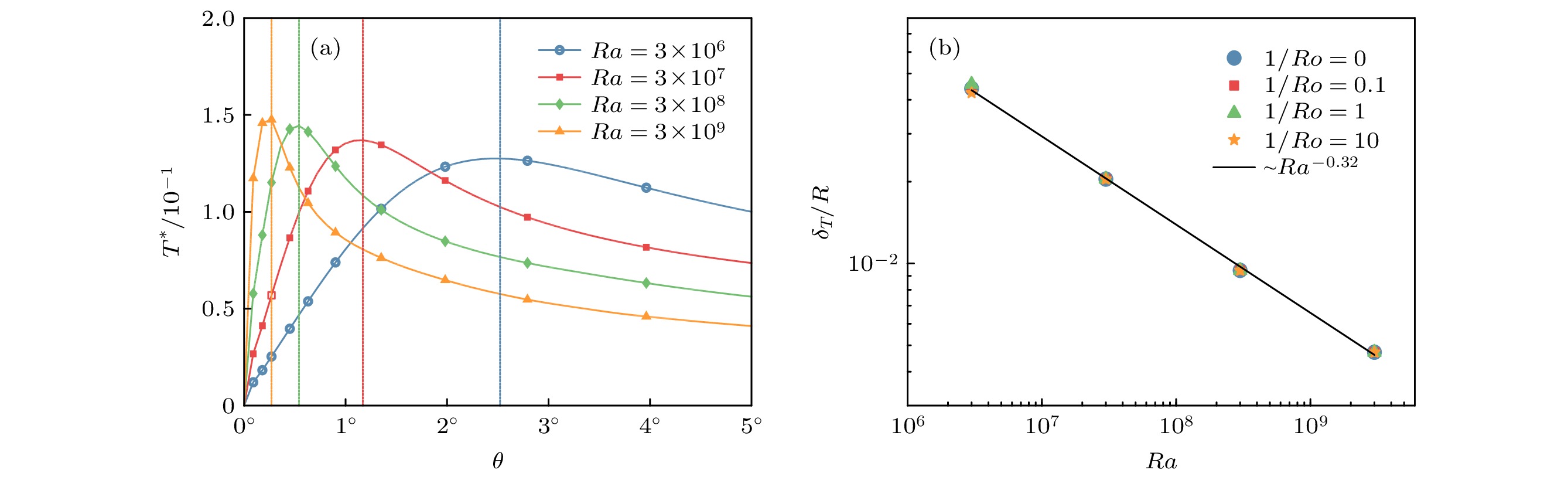
-
The soap bubble heated at the bottom is a novel thermal convection cell, which has the inherent spherical surface and quasi two-dimensional features, so that it can provide an insight into the complex physical mechanism of the planetary or atomspherical flows. This paper analyses the turbulent thermal convection on the soap bubble and addresses the properties including the thermal layer and the viscous boundary layer, the thermal dissipation and the kinetic dissipation by direct numerical simulation (DNS). The thermal dissipation and the kinetic dissipation are mostly occur in the boundary layers. They reveal the great significance of the boundary layers in the process of the energy absorption. By considering the complex characteristics of the heated bubble, this study proposes a new definition to identify the thermal boundary layer and viscous boundary layer. The thermal boundary layer thickness of
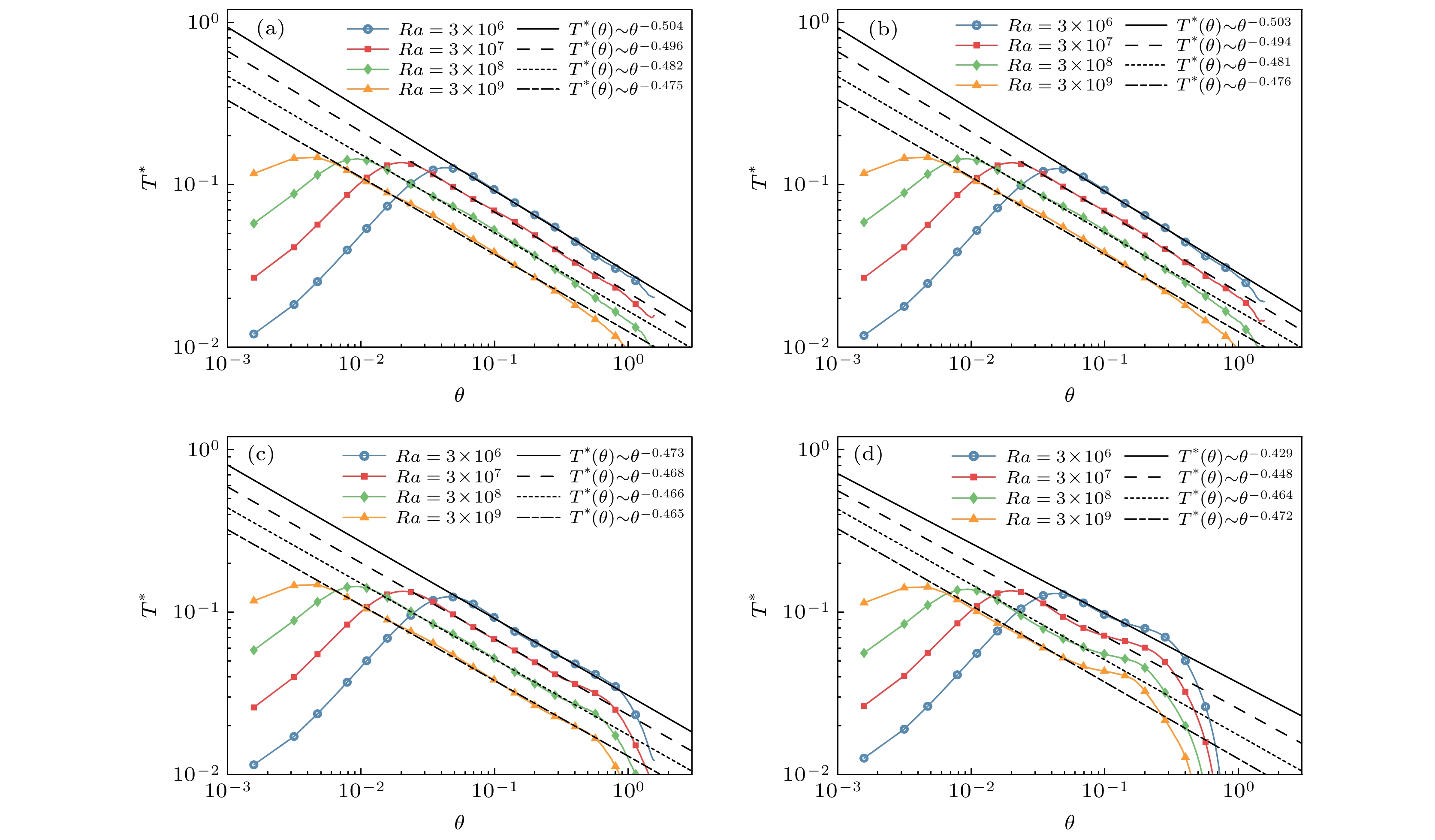
$\delta_{T}$ is defined as the geodetic distance between the equator of the bubble and the latitude at which the the mean square root temperature ($T^{*}$ ) reaches a maximum value. On the other hand, the viscous boundary layer thickness$\delta_{u}$ is the geodetic distance from the equator at the latitude where the extrapolation for the linear part of the mean square root turbulent latitude velocity ($u^{*}_{\theta}$ ) meets its maximum value. It is found that$\delta_{T}$ and$\delta_{u}$ both have a power-law dependence on the Rayleigh number. For the bubble, the scaling coefficent of$\delta_{T}$ is$-0.32$ which is consistent with that from the Rayleigh-Bénard convection model. The rotation does not affect the scaling coefficent of$\delta_{T}$ . On the other hand, the scaling coefficent of$\delta_{u}$ equals$-0.20$ and is different from that given by the Rayleigh-Bénard convection model. The weak rotation does not change the coefficent while the strong rotation makes it increase to$-0.14$ . The profile of$T^{*}$ satisfies the scaling law of$T^{*}\sim\theta^{0.5}$ with the latitude of ($\theta$ ) on the bubble. The scaling law of the mean square root temperature profile coincides with the theoretical prediction and the results obtained from the Rayleigh-Bénard convection model. However, the strong rotation is capable of shifting the scaling coefficent of the power law away from$0.5$ and shorterning the interval of satisfying the power law. Finally, it is found that the internal thermal dissipation rate and kinetic dissipation rate$\varepsilon^0_T$ and$\varepsilon^0_u$ are one order larger than their peers: the external thermal dissipation and kinetic dissipation rates$\varepsilon^1_T$ and$\varepsilon^1_u$ based on a thorough analysis of the energy budget. The major thermal dissipation and kinetic dissipation are accumulated in the boundary layers. With the rotation rate increasing, less energy is transfered from the bottom to the top of the bubble and the influence of the external energy dissipations is less pronounced.-
Keywords:
- soap bubble /
- turbulent thermal convection /
- energy dissipation rate /
- boundary layer
[1] Ma Y, Mao Z Y, Wang T, Qin J, Ding W J, Meng X Y 2020 Comput. Electr. Eng. 87 106773
Google Scholar
[2] Boffeta G, Ecke R E 2012 Annu. Rev. Fluid Mech. 44 427
Google Scholar
[3] Meuel T, Xiong Y L, Fischer P, Bruneau C H, Bessafi M, Kellay H 2013 Sci. Rep. 3 3455
Google Scholar
[4] Bruneau C H, Fischer P, Xiong Y L, Kellay H 2018 Phys. Rev. Fluids 3 043502
Google Scholar
[5] Kellay H, Goldburg W I 2002 Rep. Prog. Phys. 65 845
Google Scholar
[6] Wu X L, Martin B, Kellay H, Goldburg W I 1995 Phys. Rev. Lett. 75 236
Google Scholar
[7] Kellay H, Wu X L, Goldburg W I 1995 Phys. Rev. Lett. 74 3975
Google Scholar
[8] Kellay H 2017 Phys. Fluids 29 111113
Google Scholar
[9] Seychelles F, Amarouchene Y, Bessafi M, Kellay H 2008 Phys. Rev. Lett. 100 144501
Google Scholar
[10] Seychelles F, Ingremeau F, Pradere C, Kellay H 2010 Phys. Rev. Lett. 105 264502
Google Scholar
[11] Xiong Y L, Fischer P, Bruneau C H 2012 Proceedings of the 7th International Conference on Computational Fluid Dynamics Hawaii, United States, July 9–13, 2012 p3703
[12] Meuel T, Prado G, Seychelles F, Bessafi M, Kellay H 2012 Sci. Rep. 2 446
Google Scholar
[13] Meuel T, Coudert M, Fischer P, Bruneau C H, Kellay H 2018 Sci. Rep. 8 16513
Google Scholar
[14] He X Q, Bragg A D, Xiong Y L, Fischer P 2021 J. Fluid Mech. 924 A19
Google Scholar
[15] Frisch U, Kolmogorov A N 1995 Turbulence: The Legacy of A.N. Kolmogorov (Cambridge: Cambridge University Press) p57
[16] Pope S B 2000 Turbulent Flows (Cambridge: Cambridge University Press) p182
[17] Kolmogorov A N, Levin V, Hunt J C R, Phillips O M, Williams D 1991 Proc. R. Soc. London, Ser. A 434 9
Google Scholar
[18] Kolmogorov A N 1962 J. Fluid Mech. 13 82
Google Scholar
[19] L’vov V S 1991 Phys. Rev. Lett. 67 687
Google Scholar
[20] Lohse D, Xia K Q 2010 Annu. Rev. Fluid Mech. 42 335
Google Scholar
[21] Siggia E D 1994 Annu. Rev. Fluid Mech. 26 137
Google Scholar
[22] 周全, 夏克青 2012 力学进展 42 231
Zhou Q, Xia K Q 2012 Advances in Mechanics 42 231
[23] 谢毅超, 张路, 丁广裕, 陈鑫, 郗恒东, 夏克青 2022 力学进展
Xie Y C, Zhang L, Ding G Y, Chen X, Xi H D, Xia K Q 2022 Advances in Mechanics
[24] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[25] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[26] Grossmann S, Lohse D 2002 Phys. Rev. E 66 016305
Google Scholar
[27] Grossmann S, Lohse D 2004 Phys. Fluids 16 4462
Google Scholar
[28] Stevens R J A M, van der Poel E P, Grossmann S, Lohse D 2013 J. Fluid Mech. 730 295
Google Scholar
[29] Zhang Y, Zhou Q, Sun C 2017 J. Fluid Mech. 814 165
Google Scholar
[30] Xu A, Shi L, Xi H D 2019 Phys. Fluids 31 125101
Google Scholar
[31] He X Z, Tong P E, Xia K Q 2007 Phys. Rev. Lett. 98 144501
Google Scholar
[32] He X Z, Tong P E, Xia K Q 2009 Phys. Rev. E 79 026306
Google Scholar
[33] Hertlein A, du Puits R 2021 Phys. Fluids 33 035139
Google Scholar
[34] Shishkina O, Grossmann S, Lohse D 2016 Geophys. Res. Lett. 43 1219
Google Scholar
[35] Yang Y T, Verzicco R, Lohse D 2018 J. Fluid Mech. 848 648
Google Scholar
[36] Wang Q, Lohse D, Shishkina O 2021 Geophys. Res. Lett. 48 e2020GL091198
[37] Zhang L, Ding G Y, Xia K Q 2021 J. Fluid Mech. 914 A15
Google Scholar
[38] Stevens R J A M, Clercx H J H, Lohse D 2013 Eur. J. Mech. B/Fluids 40 41
Google Scholar
[39] King E M, Stellmach S, Buffett B 2013 J. Fluid Mech. 717 449
Google Scholar
[40] Zhong J Q, Stevens R J A M, Clercx H J H, Verzicco R, Lohse D, Ahlers G 2009 Phys. Rev. Lett. 102 044502
[41] Zhong J Q, Ahlers G 2010 J. Fluid Mech. 665 300
Google Scholar
[42] Kunnen R P J, Clercx H J H, Geurts B J Phys. Rev. E 82 036306
[43] Kunnen R P J, Stevens R J A M, Overkamp J, Sun C, van Heijst G F, Clercx H J H 2011 J. Fluid Mech. 688 422
Google Scholar
[44] Kunnen R P J, Clercx H J H, Geurts B J 2008 Europhys. Lett. 84 1
[45] 黄茂静, 包芸 2016 65 204702
Google Scholar
Huang M J, Bao Y 2016 Acta Phys. Sin. 65 204702
Google Scholar
[46] 包芸, 何建超, 高振源 2019 68 164701
Google Scholar
Bao Y, He J C, Gao Z Y 2019 Acta Phys. Sin. 68 164701
Google Scholar
[47] 包芸, 高振源, 叶孟翔 2018 67 014701
Google Scholar
Bao Y, Gao Z Y, Ye M X 2018 Acta Phys. Sin. 67 014701
Google Scholar
[48] Wang Y, He X Z, Tong P 2016 Phys. Rev. Fluids 1 082301
Google Scholar
[49] Zhou Q, Xia K Q 2013 J. Fluid Mech. 721 199
Google Scholar
[50] Sun C, Cheng Y H, Xia K Q 2008 J. Fluid Mech. 605 79
Google Scholar
[51] Zhou Q, Stevens R J A M, Sugiyama K, Grossmann S, Lohse D, Xia K Q 2010 J. Fluid Mech. 664 297
Google Scholar
[52] 方明卫, 何建超, 包芸 2020 69 174701
Google Scholar
Fang M W, He J C, Bao Y 2020 Acta Phys. Sin. 69 174701
Google Scholar
[53] Adrian R J 1996 Int. J. Heat Mass Transfer 39 11
[54] He Y H, Xia K Q 2019 Phys. Rev. Lett. 122 1
[55] Ni R, Huang S D, Xia K Q 2011 Phys. Rev. Lett. 107 17
[56] Petschel K, Stellmach S, Wilczek M, L’uff J, Hansen U 2013 Phys. Rev. Lett. 110 11
[57] 包芸, 宁浩, 徐炜 2014 63 154703
Google Scholar
Bao Y, Ning H, Xu W 2014 Acta Phys. Sin. 63 154703
Google Scholar
[58] Bernard C, Gemunu G, François H, Leo K, Albert L, Stefan T, Wu X Z, Stéphane Z, Gianluigi Z 1989 J. Fluid Mech. 204 1
Google Scholar
[59] Xin Y B, Xia K Q 1997 Phys. Rev. E 56 3010
[60] Qiu X L, Xia K Q 1998 Phys. Rev. E 58 5816
Google Scholar
-
图 1 不同坐标系下的计算域与球极投影平面投影示意图
Figure 1. Computational domain under different coordinate system and the illustration of the stereographical projection
图 2 网格结点分布图
Figure 2. Node distribution inside a grid cell
图 3 不同
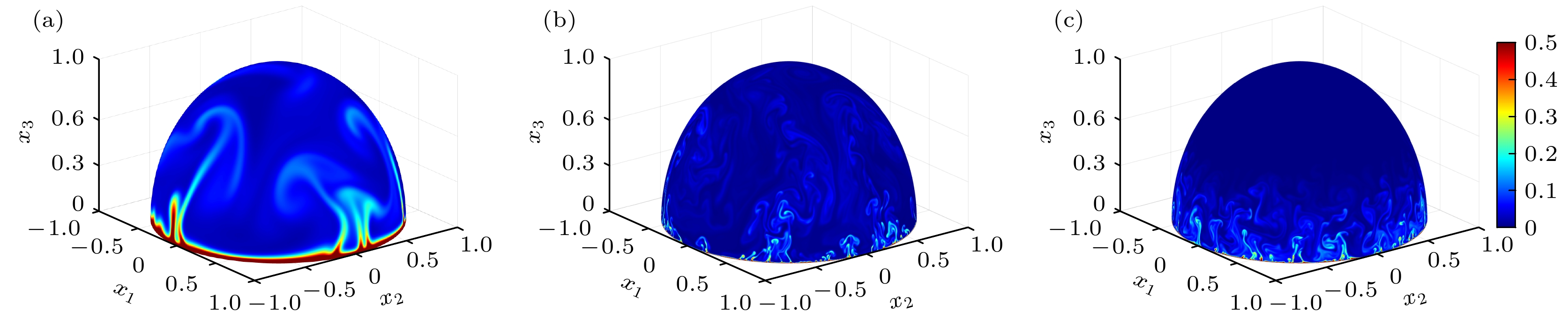
$1/Ro$ 与$Ra$ 下, T在肥皂泡上的分布$({\rm{a}})$ 算例$Ra=3\times10^6$ ,$1/Ro=0$ ;$({\rm{b}})$ 算例$Ra=3\times10^9$ ,$1/Ro=0$ ;$({\rm{c}})$ 算例$Ra=3\times10^9$ ,$1/Ro=10$ Figure 3. The instantanous temperature field with different
$1/Ro$ and$Ra$ :$({\rm{a}})$ The case of$Ra=3\times10^6$ ,$1/Ro=0$ ;$({\rm{b}})$ the case of$Ra=3\times10^9$ ,$1/Ro=0$ ;$({\rm{c}})$ the case of$Ra=3\times10^9$ ,$1/Ro=10$ .
图 4 不同
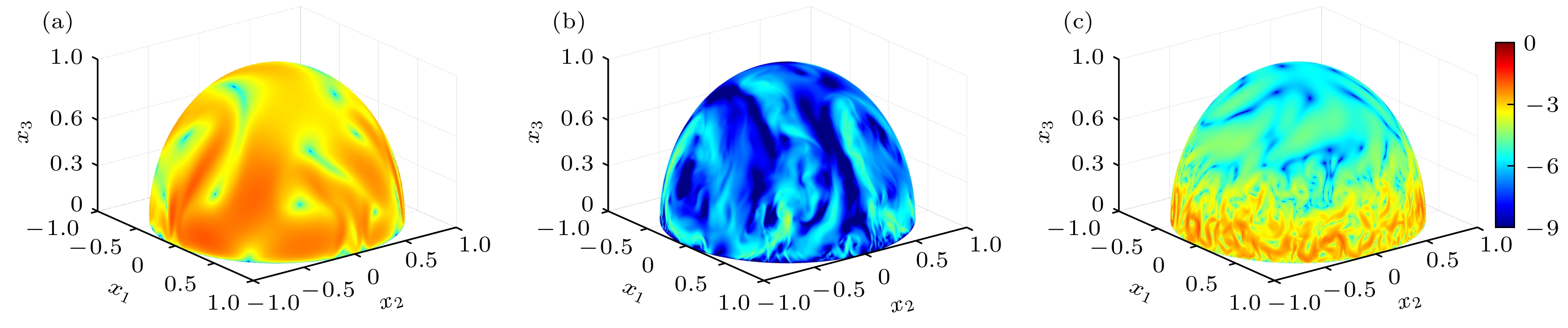
$1/Ro$ 与$Ra$ 下,$\log{E_k}$ 在肥皂泡上的分布$({\rm{a}})$ 算例$Ra=3\times10^6$ ,$1/Ro=0$ ;$({\rm{b}})$ 算例$Ra=3\times10^9$ ,$1/Ro=0$ ;$({\rm{c}})$ 算例$Ra=3\times10^9$ ,$1/Ro=10$ Figure 4. The instantanous filed of
$\log{E_k}$ with different$1/Ro$ and$Ra$ :$({\rm{a}})$ The case of$Ra=3\times10^6$ ,$1/Ro=0$ ;$({\rm{b}})$ the case of$Ra=3\times10^9$ ,$1/Ro=0$ ;$({\rm{c}})$ the case of$Ra=3\times10^9$ ,$1/Ro=10$ .
图 5 不同
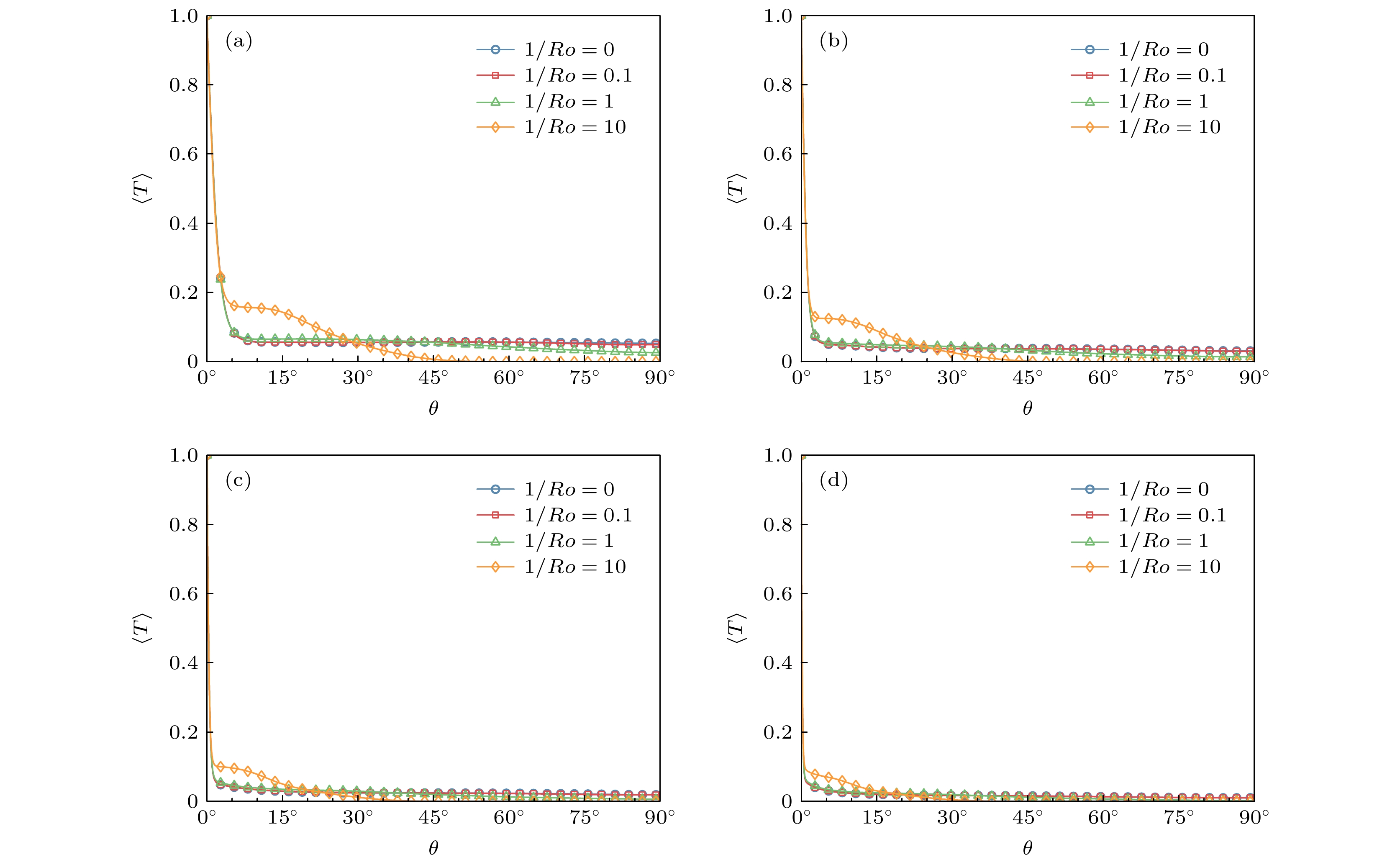
$1/Ro$ 和$Ra$ 下, 平均温度$\langle T\rangle$ 随纬度$\theta$ 的变化规律$({\rm{a}})$ 算例$Ra=3\times10^6$ ;$({\rm{b}})$ 算例$Ra=3\times10^7$ ;$({\rm{c}})$ 算例$Ra=3\times $ $ 10^8$ ;$({\rm{d}})$ 算例$Ra=3\times10^9$ Figure 5. The variation of mean temperature
$\langle T\rangle$ with the latitude$\theta$ for the different$1/Ro$ and$Ra$ :$({\rm{a}})$ The cases of$Ra=3\times10^6$ ;$({\rm{b}})$ the cases of$Ra=3\times10^7$ ;$({\rm{c}})$ the cases of$Ra=3\times10^8$ ;$({\rm{d}})$ the cases of$Ra=3\times10^9$ 
图 6
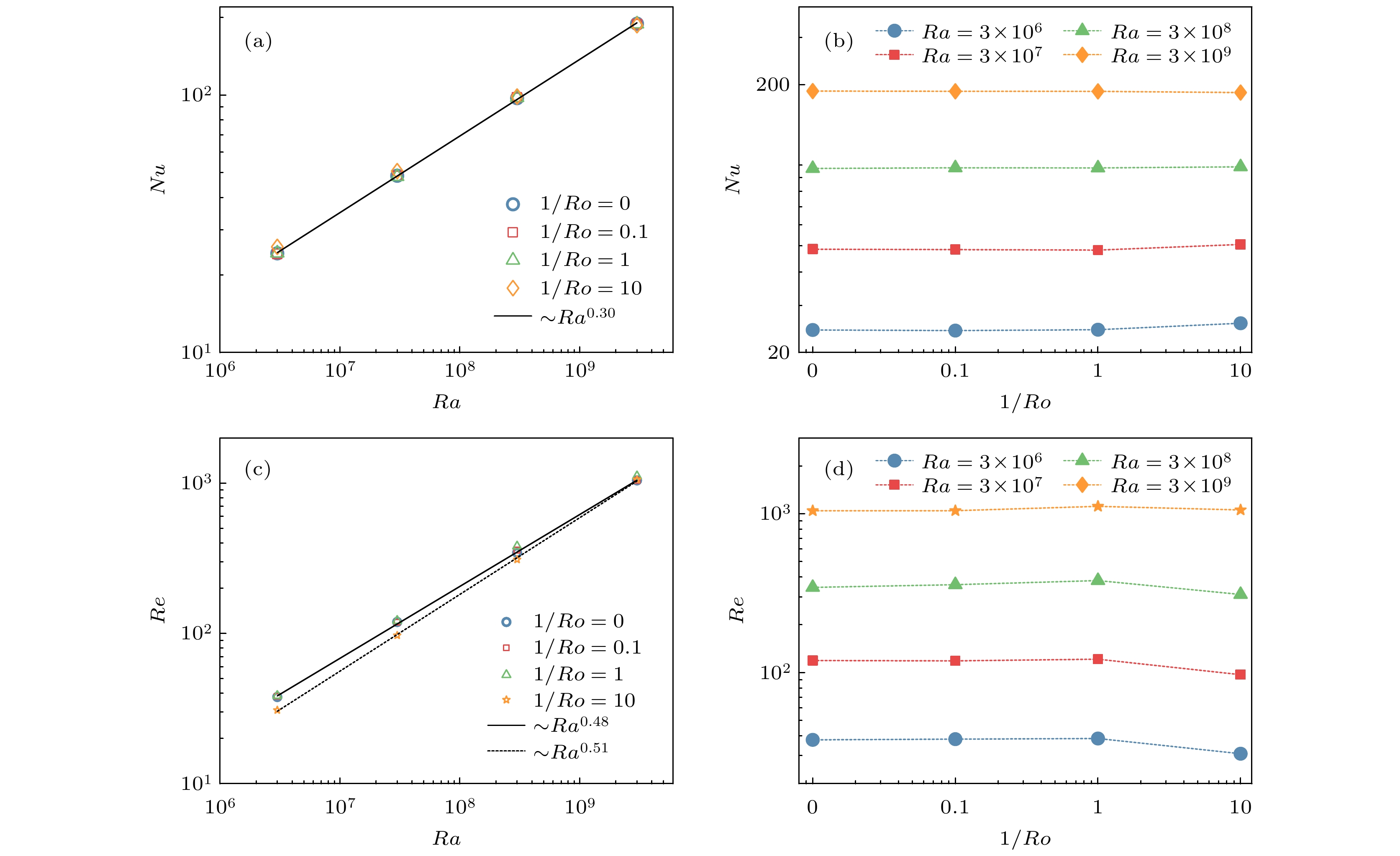
$Nu$ (上)和$Re$ (下)随$Ra$ (左)和$1/Ro$ (右)的变化规律 (a) 在$1/Ro$ 恒定的条件下,$Nu$ 随$Ra$ 的标度规律; (b) 在$Ra$ 恒定的条件下,$Nu$ 随$1/Ro$ 的变化规律; (c) 在$1/Ro$ 恒定的条件下,$Re$ 随$Ra$ 的标度规律; (d) 在$Ra$ 恒定的条件下,$Re$ 随$Ra$ 的变化规律Figure 6. The variation of
$Nu$ (up) and$Re$ (down) with$Ra$ (left) and$1/Ro$ (right): (a) The scaling behavior of$Nu$ with$Ra$ in condition of fixed$1/Ro$ ; (b) the variation of$Nu$ with$1/Ro$ in condition of fixed$Ra$ ; (c) the scaling behavior of$Re$ with$Ra$ in condition of fixed$1/Ro$ ; (d) the variation of$Re$ with$1/Ro$ in condition of fixed$Ra$ 
图 7 (a)均方根温度剖面分布与温度边界层定义示意图; (b)不同
$1/Ro$ 下, 温度边界层厚度随$Ra$ 变化规律Figure 7. (a) The variation of
$T^{*}$ profile with$Ra$ ; (b) the thickness of the thermal boundary layers with$Ra$ and$1/Ro$ 
图 8 不同
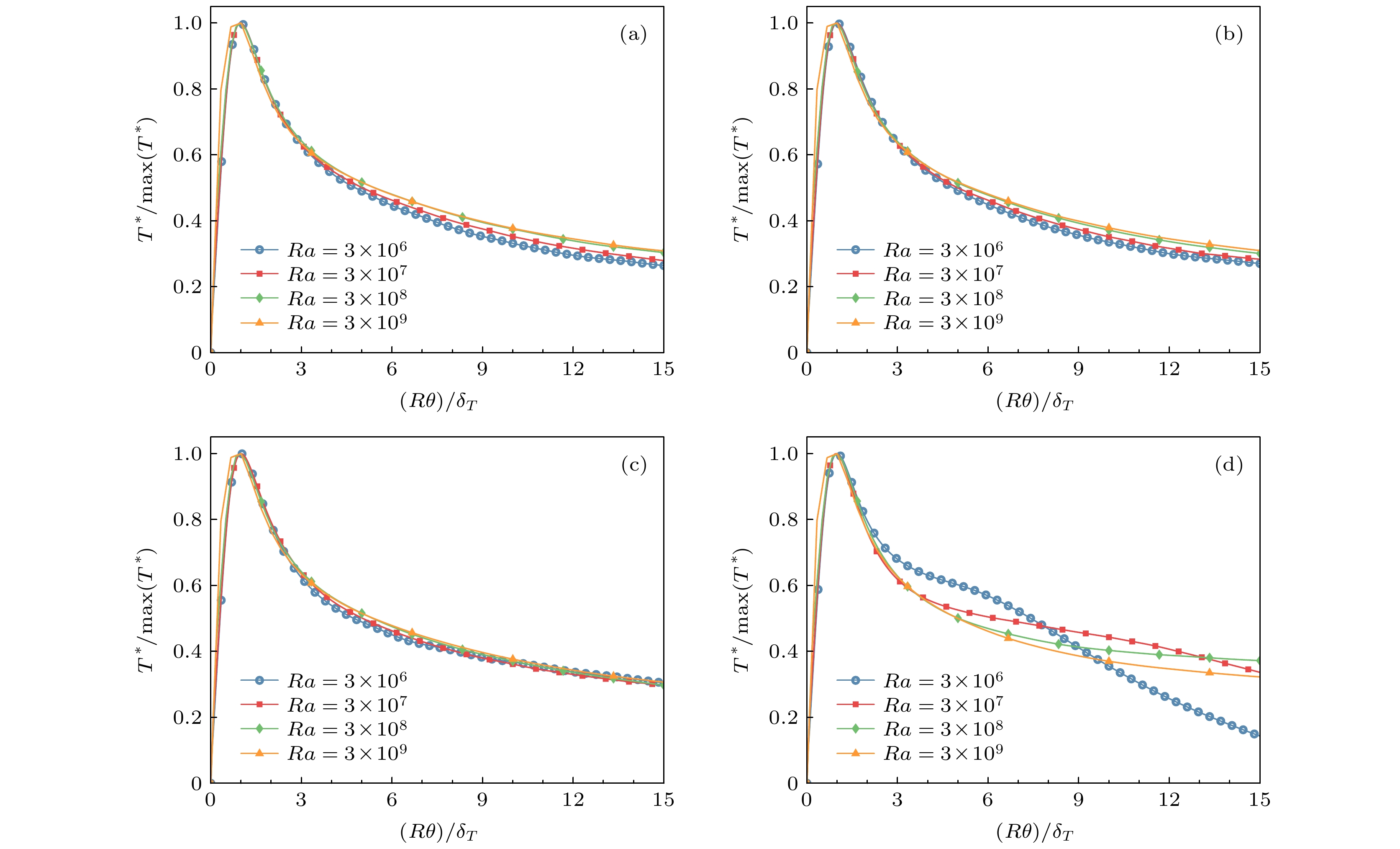
$1/Ro$ 和$Ra$ 条件下, 使用$\delta_{T}$ 与$\max(T^{*})$ 进行归一化之后的$T^{*}$ 曲线 (a)$1/Ro=0$ ; (b)$1/Ro=0.1$ ; (c)$1/Ro=1$ ; (d)$1/Ro=10$ Figure 8. The RMS temperature distribution normalized by
$\delta_{T}$ and$\max(T^{*})$ for the different$1/Ro$ and$Ra$ : (a)$1/Ro=0$ ; (b)$1/Ro=0.1$ ; (c)$1/Ro=1$ ; (d)$1/Ro=10$ 
图 9 不同
$1/Ro$ 和$Ra$ 条件下,$T^{*}$ 的剖面曲线 (a)$1/Ro=0$ ; (b)$1/Ro=0.1$ ; (c)$1/Ro=1$ ; (d)$1/Ro=10$ Figure 9. The profile of
$T^{*}$ for the different$1/Ro$ and$Ra$ : (a)$1/Ro=0$ ; (b)$1/Ro=0.1$ ; (c)$1/Ro=1$ ; (d)$1/Ro=10$ 
图 10 不同
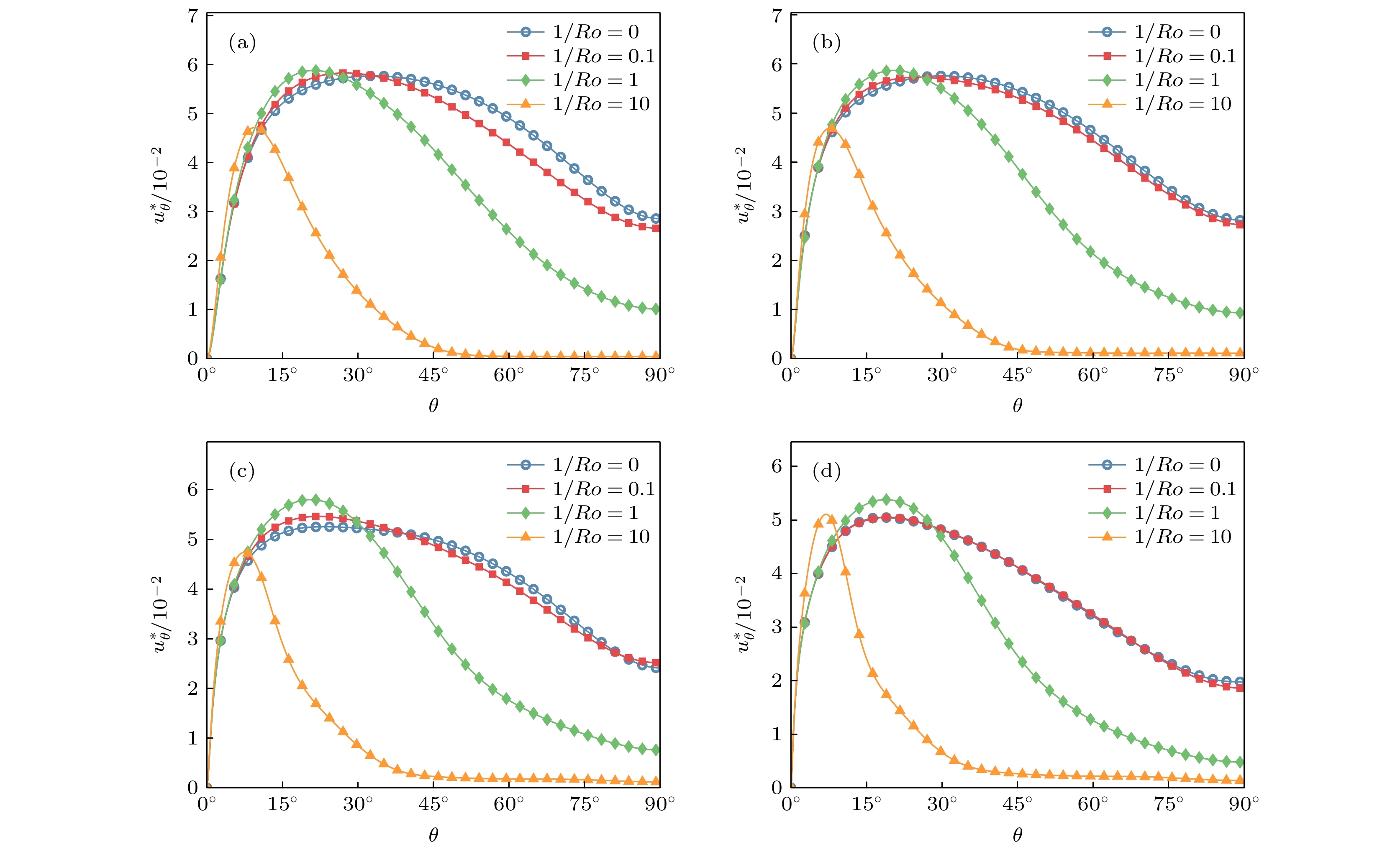
$Ra$ 与$1/Ro$ 条件下, 均方根纬度速度$u^{*}_{\theta}$ 纬度剖面曲线 (a)$Ra=3\times10^6$ ; (b)$Ra=3\times10^7$ ; (c)$Ra=3\times10^8$ ; (d)$Ra=3\times10^9$ Figure 10. The profile of the RMS velocity in the latitude direction
$u^{*}_{\theta}$ for the differnet$Ra$ and$1/Ro$ : (a)$Ra=3\times10^6$ ; (b)$Ra= $ $ 3\times10^7$ ; (c)$Ra=3\times10^8$ ; (d)$Ra=3\times10^9$ 
图 11 (a)黏性边界层厚度
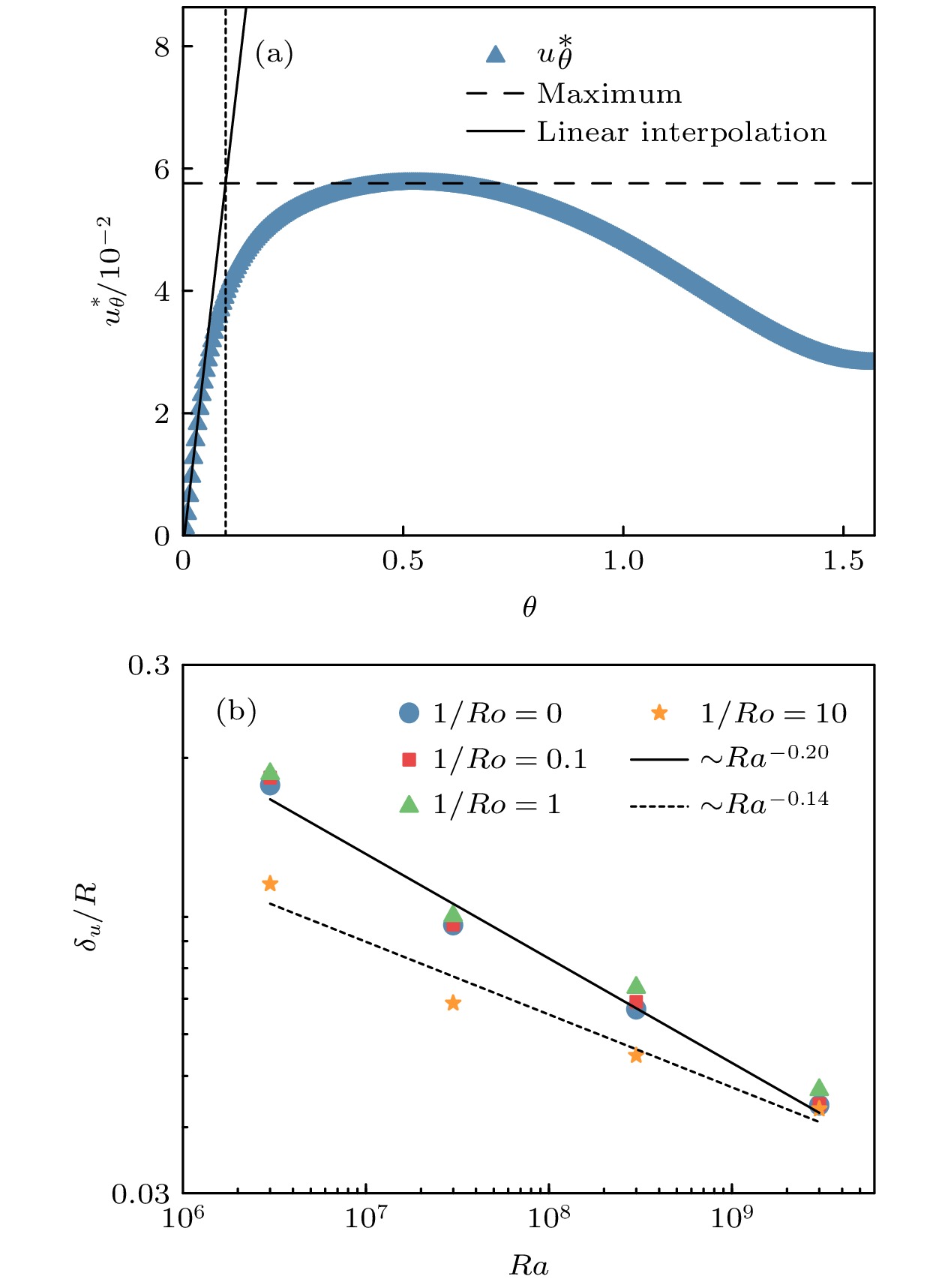
$\delta_u$ 的定义方法(示意算例$Ra=3\times10^7$ ,$1/Ro=0$ ); (b)不同$1/Ro$ 下$\delta_u$ 随$Ra$ 变化规律Figure 11. (a) The definition of the viscous boundary layer thicknesses
$\delta_u$ with the example case of$Ra=3\times10^7$ and$1/Ro=0$ ; (b) the variation of$\delta_u$ with$Ra$ for the different$1/Ro$ 
图 12 不同
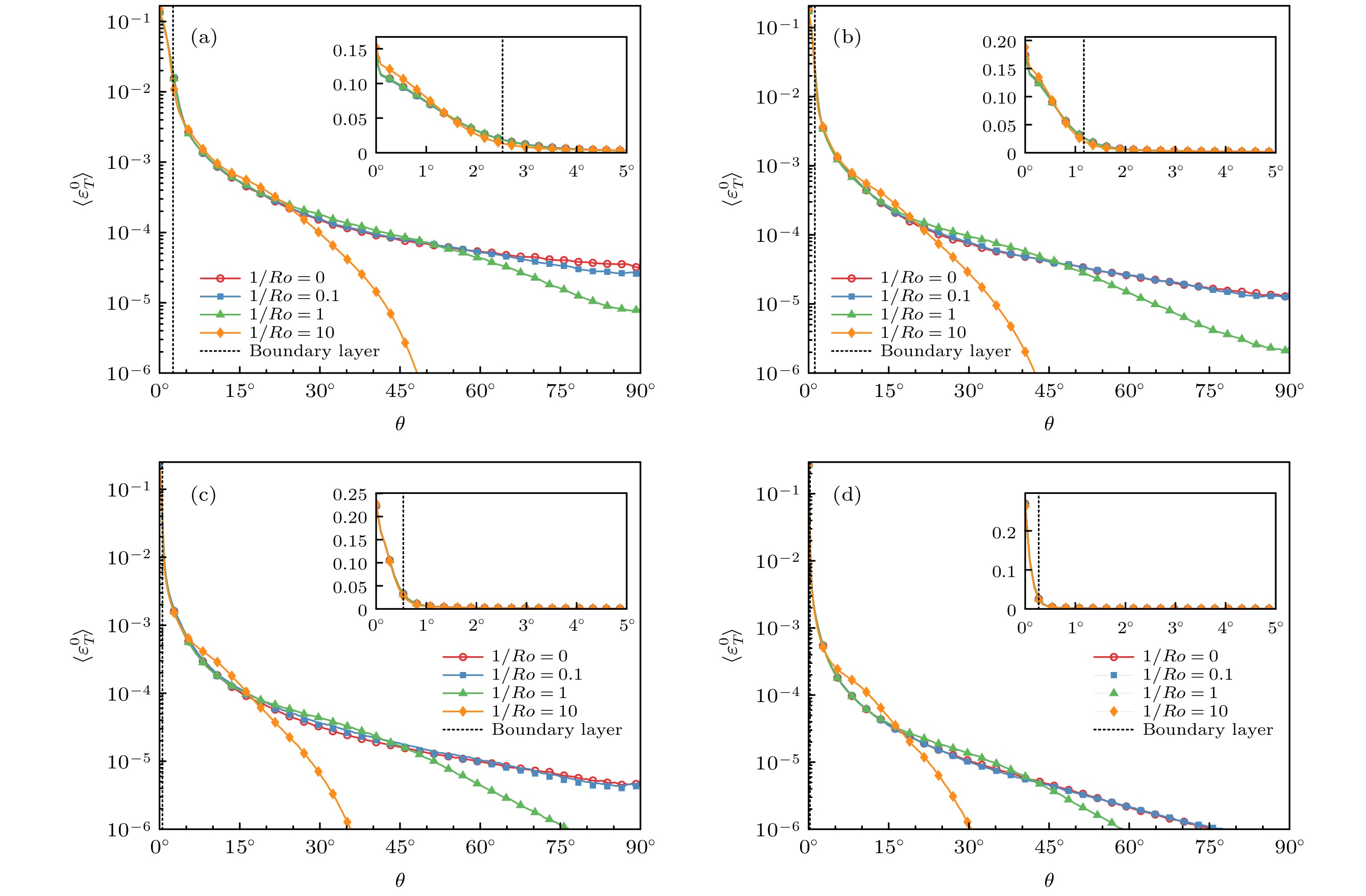
$Ra$ 与$1/Ro$ 条件下, 拟热能内耗散率$\varepsilon_{T}^{0}$ 在纬度方向的分布 (a)$Ra=3\times10^6$ ; (b)$Ra=3\times10^7$ ; (c)$Ra=3\times $ $ 10^8$ ; (d)$Ra=3\times10^9$ . 子图为边界层附近的放大Figure 12. The distribution of the internal thermal energy dissipation rate
$\varepsilon_{T}^{0}$ in the latitude direction for the different$1/Ro$ and$Ra$ : (a)$Ra=3\times10^6$ ; (b)$Ra=3\times10^7$ ; (c)$Ra=3\times10^8$ ; (d)$Ra=3\times10^9$ . The insets are the zoom-in for the boundary layers
图 13 不同
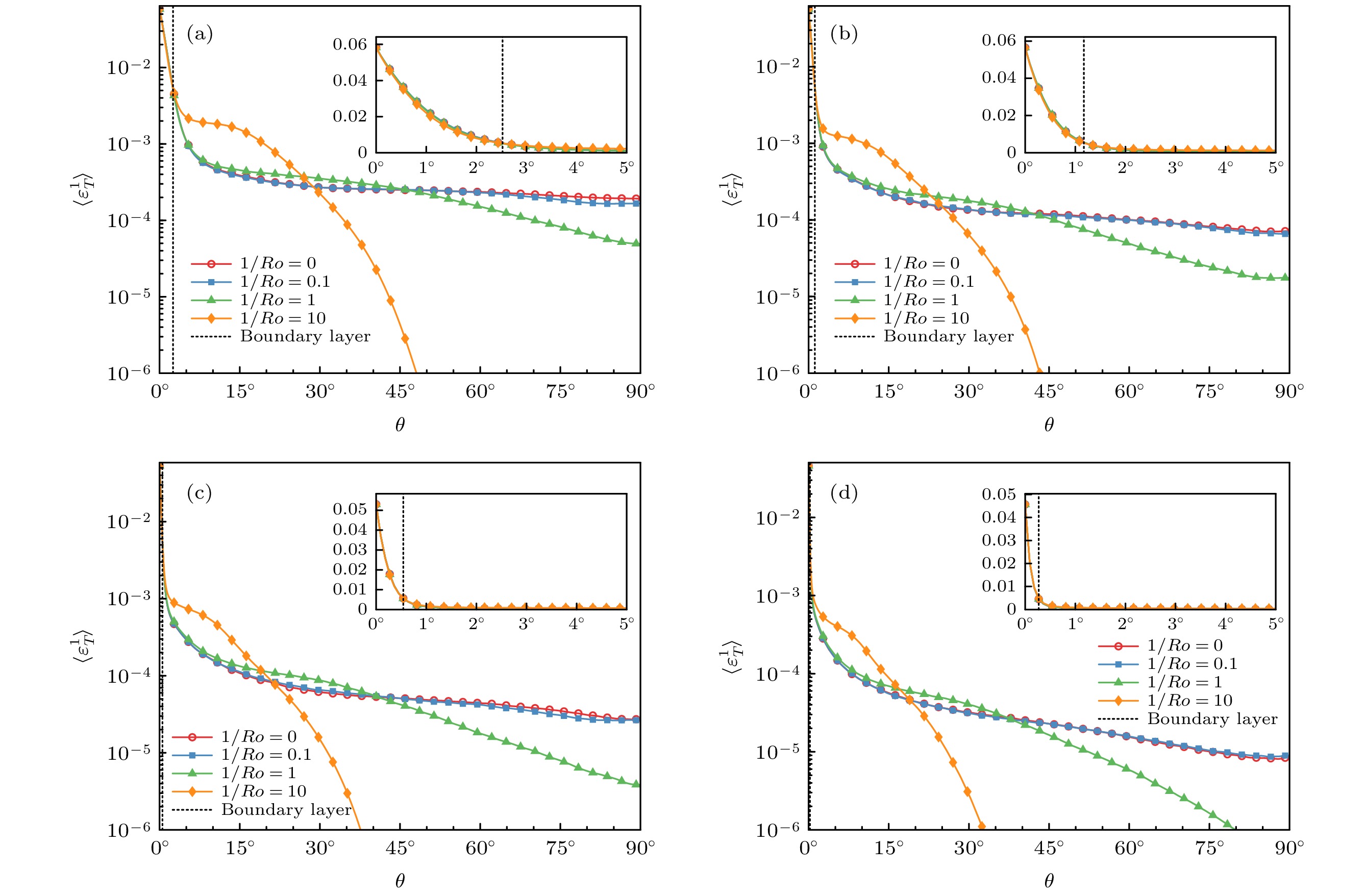
$Ra$ 与$1/Ro$ 条件下, 拟热能内耗散率$\varepsilon_{T}^{1}$ 在纬度方向的分布 (a)$Ra=3\times10^6$ ; (b)$Ra=3\times10^7$ ; (c)$Ra=3\times $ $ 10^8$ ; (d)$Ra=3\times10^9$ . 内插图为边界层附近的放大Figure 13. The distribution of the internal thermal energy dissipation rate
$\varepsilon_{T}^{1}$ in the latitude direction for the different$1/Ro$ and$Ra$ : (a)$Ra=3\times10^6$ ; (b)$Ra=3\times10^7$ ; (c)$Ra=3\times10^8$ ; (d)$Ra=3\times10^9$ . The insets are the zoom-in for the boundary layers
图 14 不同
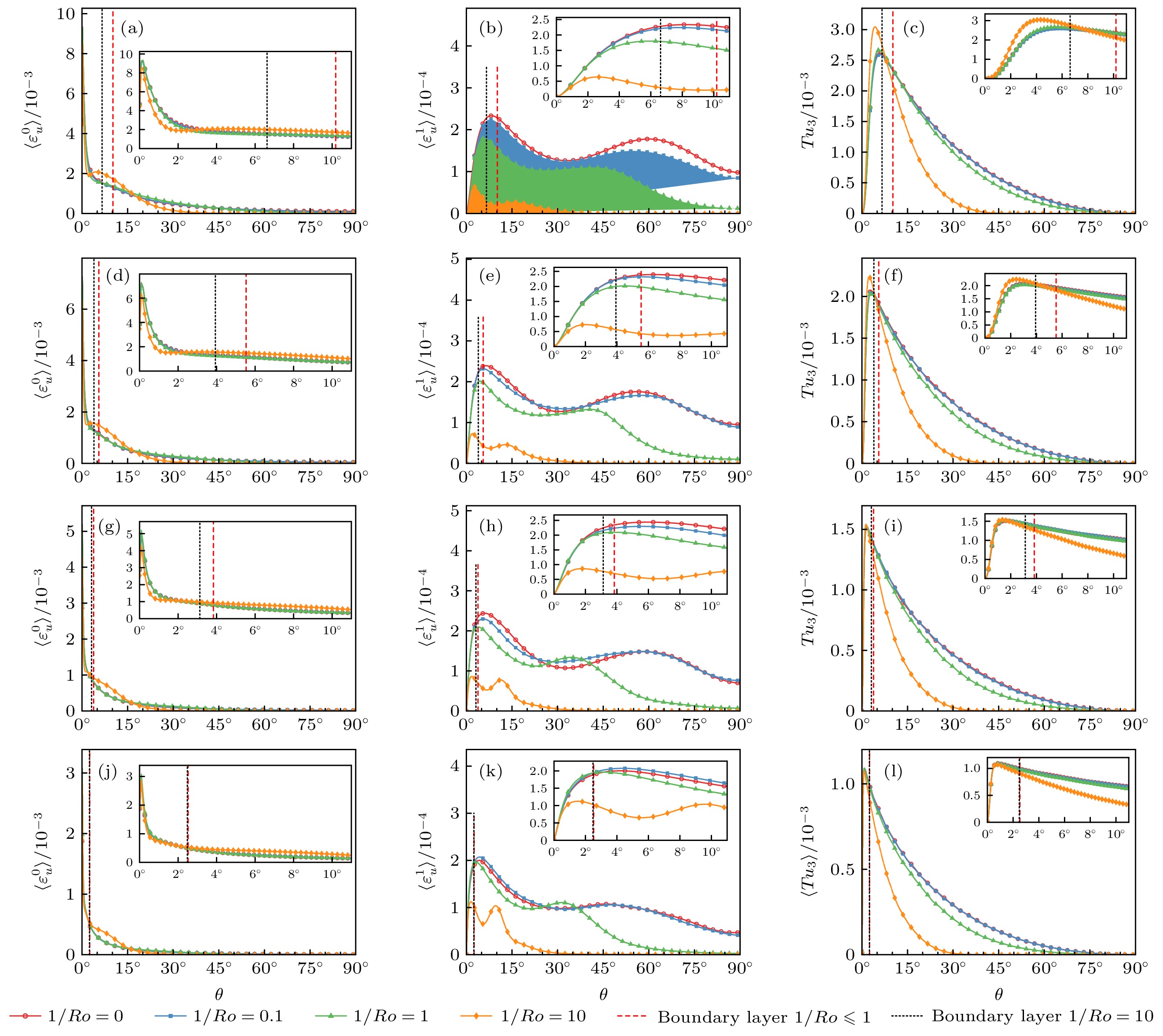
$Ra$ 与$1/Ro$ 条件下, 动能耗散率以及浮力项在纬度方向的分布 (a), (b), (c)$Ra=3\times10^6$ ; (d), (e), (f)$Ra=3\times $ $ 10^7$ ; (g), (h), (i)$Ra=3\times10^8$ ; (j), (k), (l)$Ra=3\times10^9$ . 内插图为边界层附近的放大Figure 14. The distribution of the kinetic energy dissipation rate and the buoyancy term in the latitude direction for the different
$1/Ro$ and$Ra$ : (a), (b), (c)$Ra=3\times10^6$ ; (d), (e), (f)$Ra=3\times10^7$ ; (g), (h), (i)$Ra=3\times10^8$ ; (j), (k), (l)$Ra=3\times10^9$ . The insets are the zoom-in for the boundary layers表 1 算例详细信息
Table 1. The detailed information of the cases
$Ra$ $1/Ro$ $Pr$ S F Mesh resolution $3\times10^6$ $0;0.1;1;10$ 7 0.06 0.06 $1024\times1024$ $3\times10^7$ $0;0.1;1;10$ $1024\times1024$ $3\times10^8$ $0;0.1;1;10$ $1536\times1536$ $3\times10^9$ $0;0.1;1;10$ $2048\times2048$ 
DownLoad: CSV
-
[1] Ma Y, Mao Z Y, Wang T, Qin J, Ding W J, Meng X Y 2020 Comput. Electr. Eng. 87 106773
Google Scholar
[2] Boffeta G, Ecke R E 2012 Annu. Rev. Fluid Mech. 44 427
Google Scholar
[3] Meuel T, Xiong Y L, Fischer P, Bruneau C H, Bessafi M, Kellay H 2013 Sci. Rep. 3 3455
Google Scholar
[4] Bruneau C H, Fischer P, Xiong Y L, Kellay H 2018 Phys. Rev. Fluids 3 043502
Google Scholar
[5] Kellay H, Goldburg W I 2002 Rep. Prog. Phys. 65 845
Google Scholar
[6] Wu X L, Martin B, Kellay H, Goldburg W I 1995 Phys. Rev. Lett. 75 236
Google Scholar
[7] Kellay H, Wu X L, Goldburg W I 1995 Phys. Rev. Lett. 74 3975
Google Scholar
[8] Kellay H 2017 Phys. Fluids 29 111113
Google Scholar
[9] Seychelles F, Amarouchene Y, Bessafi M, Kellay H 2008 Phys. Rev. Lett. 100 144501
Google Scholar
[10] Seychelles F, Ingremeau F, Pradere C, Kellay H 2010 Phys. Rev. Lett. 105 264502
Google Scholar
[11] Xiong Y L, Fischer P, Bruneau C H 2012 Proceedings of the 7th International Conference on Computational Fluid Dynamics Hawaii, United States, July 9–13, 2012 p3703
[12] Meuel T, Prado G, Seychelles F, Bessafi M, Kellay H 2012 Sci. Rep. 2 446
Google Scholar
[13] Meuel T, Coudert M, Fischer P, Bruneau C H, Kellay H 2018 Sci. Rep. 8 16513
Google Scholar
[14] He X Q, Bragg A D, Xiong Y L, Fischer P 2021 J. Fluid Mech. 924 A19
Google Scholar
[15] Frisch U, Kolmogorov A N 1995 Turbulence: The Legacy of A.N. Kolmogorov (Cambridge: Cambridge University Press) p57
[16] Pope S B 2000 Turbulent Flows (Cambridge: Cambridge University Press) p182
[17] Kolmogorov A N, Levin V, Hunt J C R, Phillips O M, Williams D 1991 Proc. R. Soc. London, Ser. A 434 9
Google Scholar
[18] Kolmogorov A N 1962 J. Fluid Mech. 13 82
Google Scholar
[19] L’vov V S 1991 Phys. Rev. Lett. 67 687
Google Scholar
[20] Lohse D, Xia K Q 2010 Annu. Rev. Fluid Mech. 42 335
Google Scholar
[21] Siggia E D 1994 Annu. Rev. Fluid Mech. 26 137
Google Scholar
[22] 周全, 夏克青 2012 力学进展 42 231
Zhou Q, Xia K Q 2012 Advances in Mechanics 42 231
[23] 谢毅超, 张路, 丁广裕, 陈鑫, 郗恒东, 夏克青 2022 力学进展
Xie Y C, Zhang L, Ding G Y, Chen X, Xi H D, Xia K Q 2022 Advances in Mechanics
[24] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[25] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[26] Grossmann S, Lohse D 2002 Phys. Rev. E 66 016305
Google Scholar
[27] Grossmann S, Lohse D 2004 Phys. Fluids 16 4462
Google Scholar
[28] Stevens R J A M, van der Poel E P, Grossmann S, Lohse D 2013 J. Fluid Mech. 730 295
Google Scholar
[29] Zhang Y, Zhou Q, Sun C 2017 J. Fluid Mech. 814 165
Google Scholar
[30] Xu A, Shi L, Xi H D 2019 Phys. Fluids 31 125101
Google Scholar
[31] He X Z, Tong P E, Xia K Q 2007 Phys. Rev. Lett. 98 144501
Google Scholar
[32] He X Z, Tong P E, Xia K Q 2009 Phys. Rev. E 79 026306
Google Scholar
[33] Hertlein A, du Puits R 2021 Phys. Fluids 33 035139
Google Scholar
[34] Shishkina O, Grossmann S, Lohse D 2016 Geophys. Res. Lett. 43 1219
Google Scholar
[35] Yang Y T, Verzicco R, Lohse D 2018 J. Fluid Mech. 848 648
Google Scholar
[36] Wang Q, Lohse D, Shishkina O 2021 Geophys. Res. Lett. 48 e2020GL091198
[37] Zhang L, Ding G Y, Xia K Q 2021 J. Fluid Mech. 914 A15
Google Scholar
[38] Stevens R J A M, Clercx H J H, Lohse D 2013 Eur. J. Mech. B/Fluids 40 41
Google Scholar
[39] King E M, Stellmach S, Buffett B 2013 J. Fluid Mech. 717 449
Google Scholar
[40] Zhong J Q, Stevens R J A M, Clercx H J H, Verzicco R, Lohse D, Ahlers G 2009 Phys. Rev. Lett. 102 044502
[41] Zhong J Q, Ahlers G 2010 J. Fluid Mech. 665 300
Google Scholar
[42] Kunnen R P J, Clercx H J H, Geurts B J Phys. Rev. E 82 036306
[43] Kunnen R P J, Stevens R J A M, Overkamp J, Sun C, van Heijst G F, Clercx H J H 2011 J. Fluid Mech. 688 422
Google Scholar
[44] Kunnen R P J, Clercx H J H, Geurts B J 2008 Europhys. Lett. 84 1
[45] 黄茂静, 包芸 2016 65 204702
Google Scholar
Huang M J, Bao Y 2016 Acta Phys. Sin. 65 204702
Google Scholar
[46] 包芸, 何建超, 高振源 2019 68 164701
Google Scholar
Bao Y, He J C, Gao Z Y 2019 Acta Phys. Sin. 68 164701
Google Scholar
[47] 包芸, 高振源, 叶孟翔 2018 67 014701
Google Scholar
Bao Y, Gao Z Y, Ye M X 2018 Acta Phys. Sin. 67 014701
Google Scholar
[48] Wang Y, He X Z, Tong P 2016 Phys. Rev. Fluids 1 082301
Google Scholar
[49] Zhou Q, Xia K Q 2013 J. Fluid Mech. 721 199
Google Scholar
[50] Sun C, Cheng Y H, Xia K Q 2008 J. Fluid Mech. 605 79
Google Scholar
[51] Zhou Q, Stevens R J A M, Sugiyama K, Grossmann S, Lohse D, Xia K Q 2010 J. Fluid Mech. 664 297
Google Scholar
[52] 方明卫, 何建超, 包芸 2020 69 174701
Google Scholar
Fang M W, He J C, Bao Y 2020 Acta Phys. Sin. 69 174701
Google Scholar
[53] Adrian R J 1996 Int. J. Heat Mass Transfer 39 11
[54] He Y H, Xia K Q 2019 Phys. Rev. Lett. 122 1
[55] Ni R, Huang S D, Xia K Q 2011 Phys. Rev. Lett. 107 17
[56] Petschel K, Stellmach S, Wilczek M, L’uff J, Hansen U 2013 Phys. Rev. Lett. 110 11
[57] 包芸, 宁浩, 徐炜 2014 63 154703
Google Scholar
Bao Y, Ning H, Xu W 2014 Acta Phys. Sin. 63 154703
Google Scholar
[58] Bernard C, Gemunu G, François H, Leo K, Albert L, Stefan T, Wu X Z, Stéphane Z, Gianluigi Z 1989 J. Fluid Mech. 204 1
Google Scholar
[59] Xin Y B, Xia K Q 1997 Phys. Rev. E 56 3010
[60] Qiu X L, Xia K Q 1998 Phys. Rev. E 58 5816
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3628
- PDF Downloads: 45
- Cited By: 0
