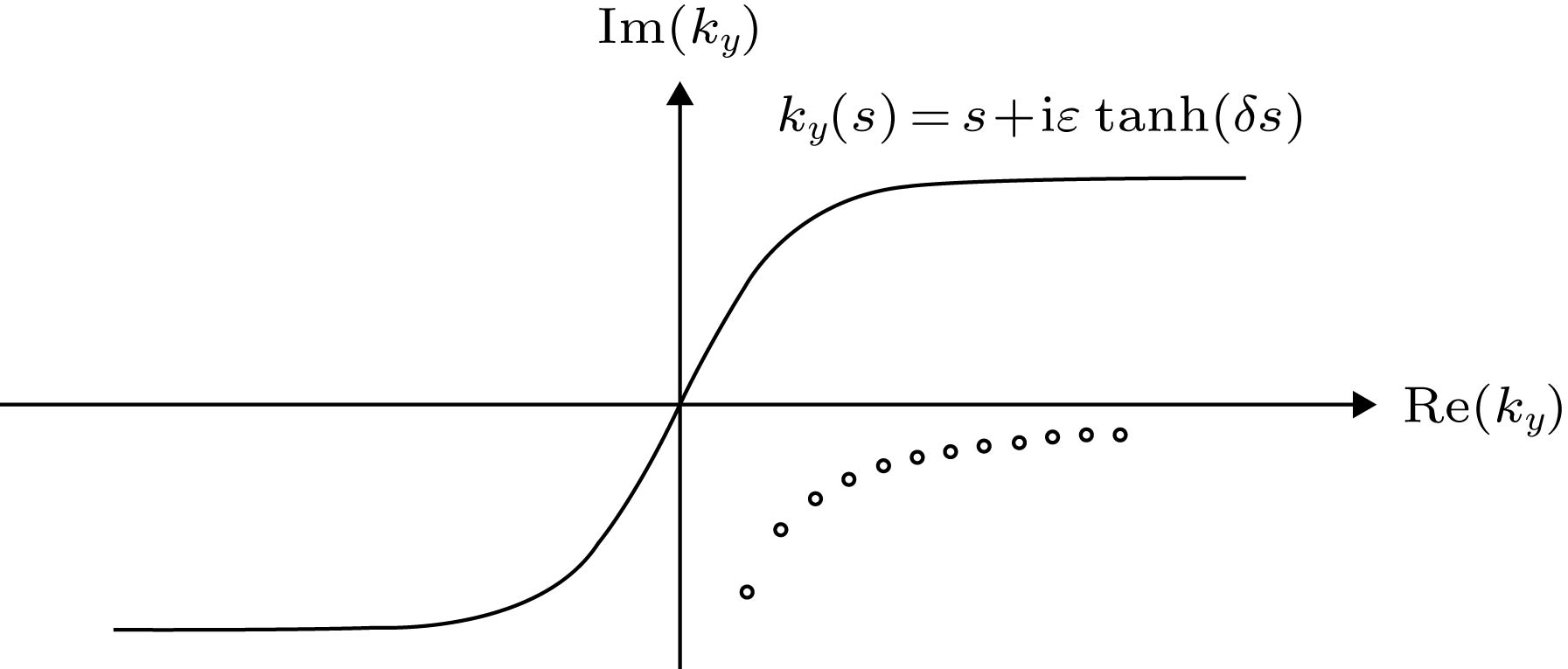
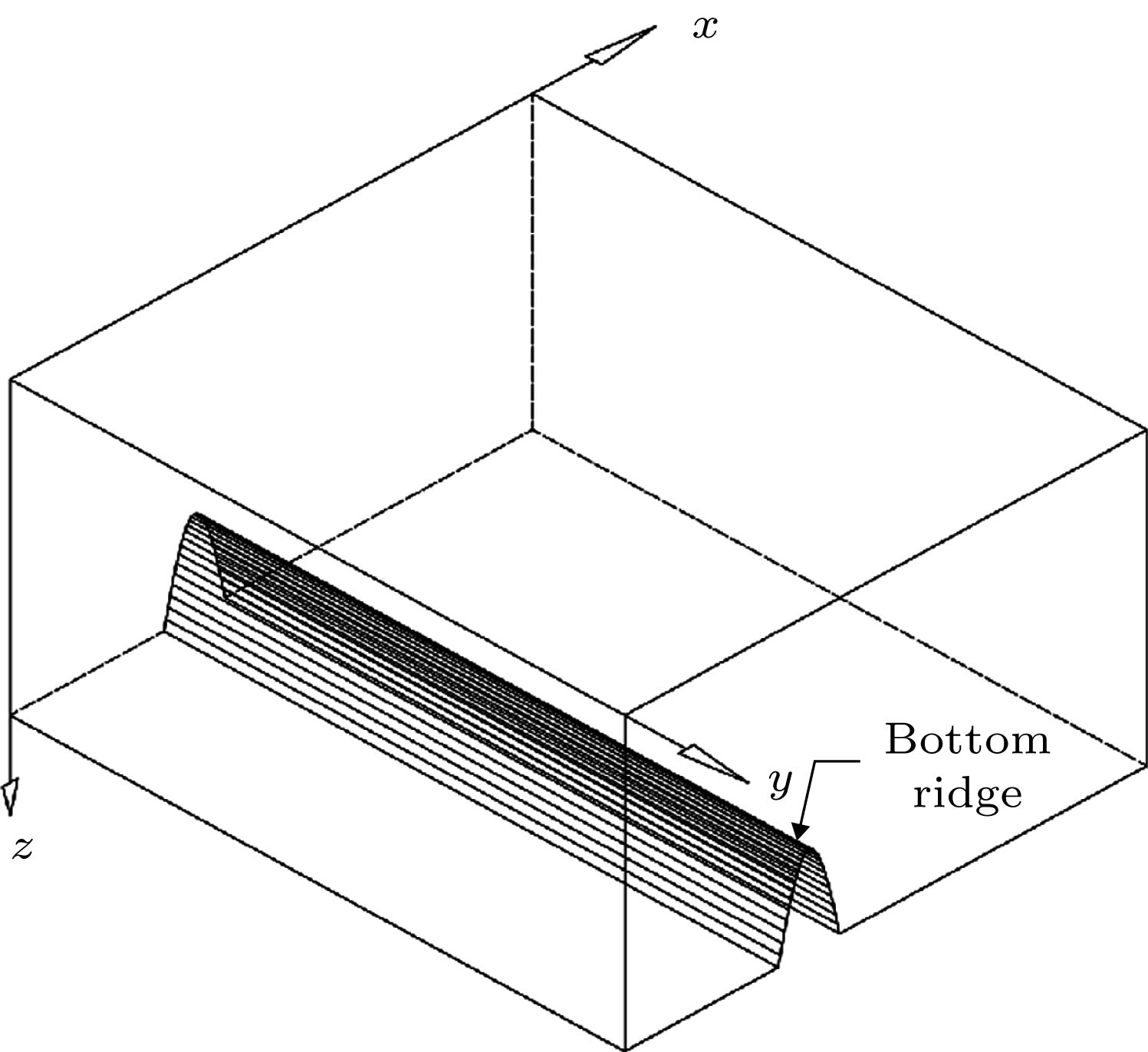
-
An accurate and numerically efficient numerical model is very important for studying the effect of internal wave on underwawter sound propagation. A full-wave, three-dimensional (3D) coupled-mode model is able to deal with the internal wave problem with satisfactory accuracy, but such a model is in general numerically inefficient. A numerically efficient 3D model is presented for sound propagation in a range-dependent waveguide in the presence of solitary internal waves in this work. The present model is a forward-marching model that neglects backscattering. In this 3D model, an efficient two-dimensional (2D) coupled-mode model, C-SNAP, is adopted to compute 2D acoustic field solutions excited by a line source. The C-SNAP is a 2D forward-marching model, which uses an energy-conserving matching condition to preserve accuracy. An appealing aspect of C-SNAP is that its efficiency is competitive with that of the existing parabolic equation model. The integral transform technique is used to extend C-SNAP to a 3D model, where a complex integration contour is used for evaluating the wavenumber integral. A brief review of C-SNAP and formulation of the present 3D model are given. The forward-marching models are primarily suitable for treating the range-dependent problems with weak backscattering, such as with a slowly varying bathymetry. Since in general the backscattering from internal wave is weak, which is also validated numerically in this work, the present model is able to address the problem of sound propagation through internal wave with satisfactory accuracy. At the same time, it achieves an efficiency gain of at least an order of magnitude over that of full two-way, 3D model. In addition to the internal wave, the present model is also suitable for solving the general range-dependent problems where backscattering is weak, such as in the presence of a bottom ridge of a small height. Numerical simulations are also provided to validate the present model, where a two-way, 3D model serves as the benchmark. The numerical results show that the effect of the internal wave on the acoustic field is negligible for the region between the source and the internal wave. However, the effect is significant on the other side of the internal wave. A more interesting observation is the angular dependence of the interference pattern induced by the internal wave.
-
Keywords:
- three-dimensional modeling /
- internal solitary wave /
- coupled modes
[1] 王宁, 张海青, 王好忠, 高大治 2010 声学学报 35 38
Wang N, Zhang H Q, Wang H Z, Gao D Z 2010 Acta Acust. 35 38
[2] 马树青, 杨士莪, 朴胜春, 李婷婷 2009 振动与冲击 28 73
Google Scholar
Ma S Q, Yang S E, Piao S C, Li T T 2009 J. Vib. Shock 28 73
Google Scholar
[3] Badiey M, Katsnelson B G, Lynch J F, Pereselkov S, Siegmann W L 2005 J. Acoust. Soc. Am. 117 613
Google Scholar
[4] Luo J, Badiey M, Karjadi E A, Katsnelson B, Tskhoidze A, Lynch J F, Moum J N 2008 J. Acoust. Soc. Am. 124 66
Google Scholar
[5] Lin Y T, Duda T F, Lynch J F 2009 J. Acoust. Soc. Am. 126 1752
Google Scholar
[6] Colosi J A 2008 J. Acoust. Soc. Am. 124 1452
Google Scholar
[7] Yang T C 2014 J. Acoust. Soc. Am. 135 610
Google Scholar
[8] Siegmann W L, Kriegsmann G A, Lee D 1985 J. Acoust. Soc. Am. 78 659
Google Scholar
[9] Lee D, Botseas G, Siegmann W L 1992 J. Acoust. Soc. Am. 91 3192
Google Scholar
[10] Collins M D, Chin-Bing S A 1990 J. Acoust. Soc. Am. 87 1104
Google Scholar
[11] Ferla C M, Porter M B, Jensen F B 1993 C-SNAP: Coupled SACLANTCEN Normal Mode Propagation Loss Model (La Spezia: SACLANT Undersea Research Center) pp1–46
[12] Luo W Y, Yang C M, Qin J X, Zhang R H 2012 Sci. Chin. Phys. Mech. Astron. 55 572
Google Scholar
[13] 杨春梅, 骆文于, 张仁和, 秦继兴 2014 声学学报 39 295
Yang C M, Luo W Y, Zhang R H, Qin J X 2014 Acta Acust. 39 295
[14] Luo W Y, Zhang R H 2015 Sci. China-G: Phys. Mech. Astron. 58 1
[15] Evans R B 1983 J. Acoust. Soc. Am. 74 188
Google Scholar
[16] Collins M D, Westwood E K 1991 J. Acoust. Soc. Am. 89 1068
Google Scholar
[17] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics （2nd ed.） (New York: Springer) pp337–445
[18] Buckingham M J 1989 J. Acoust. Soc. Am. 86 2273
Google Scholar
[19] Luo W Y, Yu X L, Yang X F, Zhang Z Z, Zhang R H 2016 Chin. Phys. B 25 124309
Google Scholar
[20] Jensen F B 1998 J. Acoust. Soc. Am. 104 1310
Google Scholar
-
图 1 水平变化波导(红色虚线)的阶梯近似
Figure 1. Stair step approximation of a sloping bottom (red dashed line)
图 2 反傅里叶变换的积分围线(圆圈代表简正波的本征值, 即水平波数)
Figure 2. Complex integration contour for evaluation of the wavenumber integral. The dots indicate horizontal wavenumbers of the normal modes.
图 3 二维声速剖面示意图 (a)无孤子内波的声速剖面; (b)孤子内波位于4 km处的声速剖面; (c)孤子内波位于4 km处, 海脊位于6 km处的声速剖面
Figure 3. Sound speed fields considered in this paper: (a) The background sound speed field; (b) in the presence of an internal wave soliton, centered at range 4 km from the source; (c) in the presence of both an internal wave soliton centered at 4 km and a cosine-bell shaped bottom ridge centered at 6 km from the source.
图 4 孤子内波环境下DGMCM2D和C-SNAP在70 m深度传播损失曲线 蓝色实线和红色虚线分别表示无孤子内波时DGMCM2D和C-SNAP的计算结果, 绿色和枚红色虚线分别表示孤子内波波包在4 km时DGMCM2D和C-SNAP的计算结果, 黑色虚线表示孤子内波波包位置
Figure 4. Transmission loss results for the internal solitary wave problem computed by DGMCM2D and C-SNAP. The blue solid line and red dashed line are the results by DGMCM2D and C-SNAP for the case without internal waves, respectively, and the green and magenta dashed lines are the results by DGMCM2D and C-SNAP for the case with a soliton located at range 4 km, respectively. The black dashed line indicates the center of the soliton.
图 5 70 m深度水平面上的三维传播损失结果 (a) DGMCM3D的结果; (b)本文提出的三维模型的结果, 黑色虚线代表孤子内波波包的位置
Figure 5. Three-dimensional transmission loss results in the horizontal plane at depth 70 m computed by (a) DGMCM3D and (b) the present 3D model. The center location of the internal wave is indicated by dashed black lines.
图 6 纵向距离
$ y = 0 \;{\rm{km}}$ , 深度z = 70 m, 随距离传播的损失曲线, 蓝色实线和红色虚线分别为DGMCM3D和本文提出的三维模型的结果Figure 6. Transmission loss lines versus range along the cross-range
$ y = 0 \;{\rm{km}}$ at depth z = 70 m computed by DGMCM3D (the blue, solid curve) and the present 3D model (the red, dashed curve).
图 7 海底存在海脊的水平变化波导示意图
Figure 7. Geometry of a range-dependent waveguide with a bottom ridge.
图 8 孤子内波和海脊同时存在时深度70 m处的二维传播损失结果, 其中蓝色实线为DGMCM2D结果, 红色虚线为C-SNAP结果
Figure 8. Two-dimensional transmission loss results at a depth of 70 m for the problem involving a solitary internal wave as well as a bottom ridge by DGMCM2D (the blue, solid curve) and C-SNAP (the red, dashed curve).
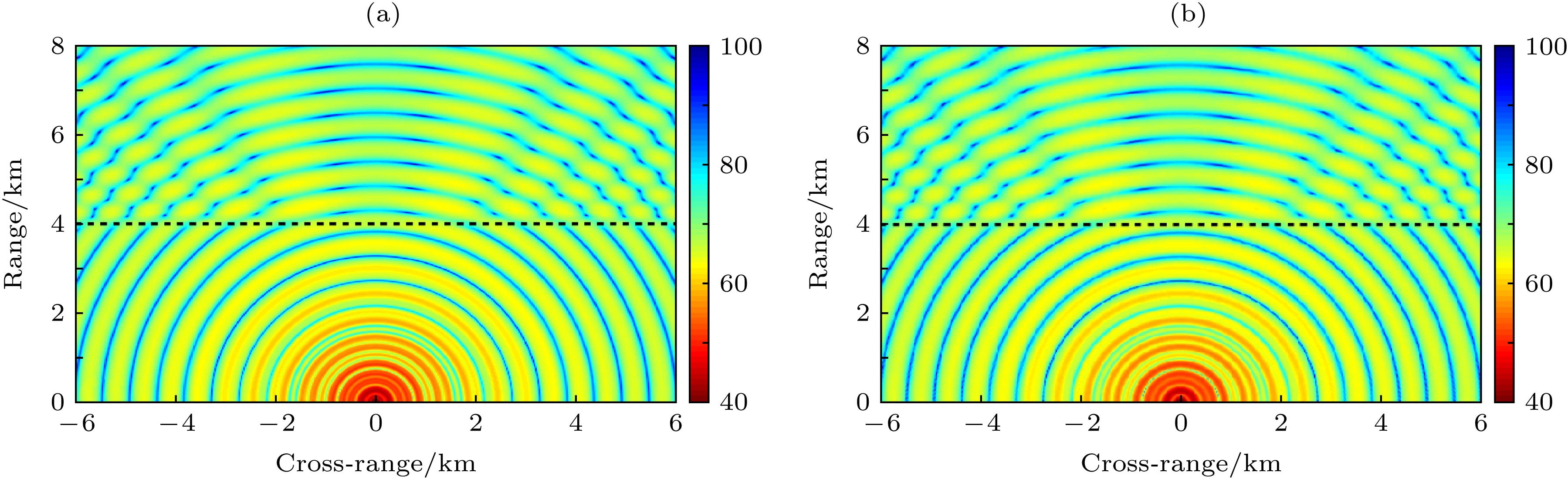
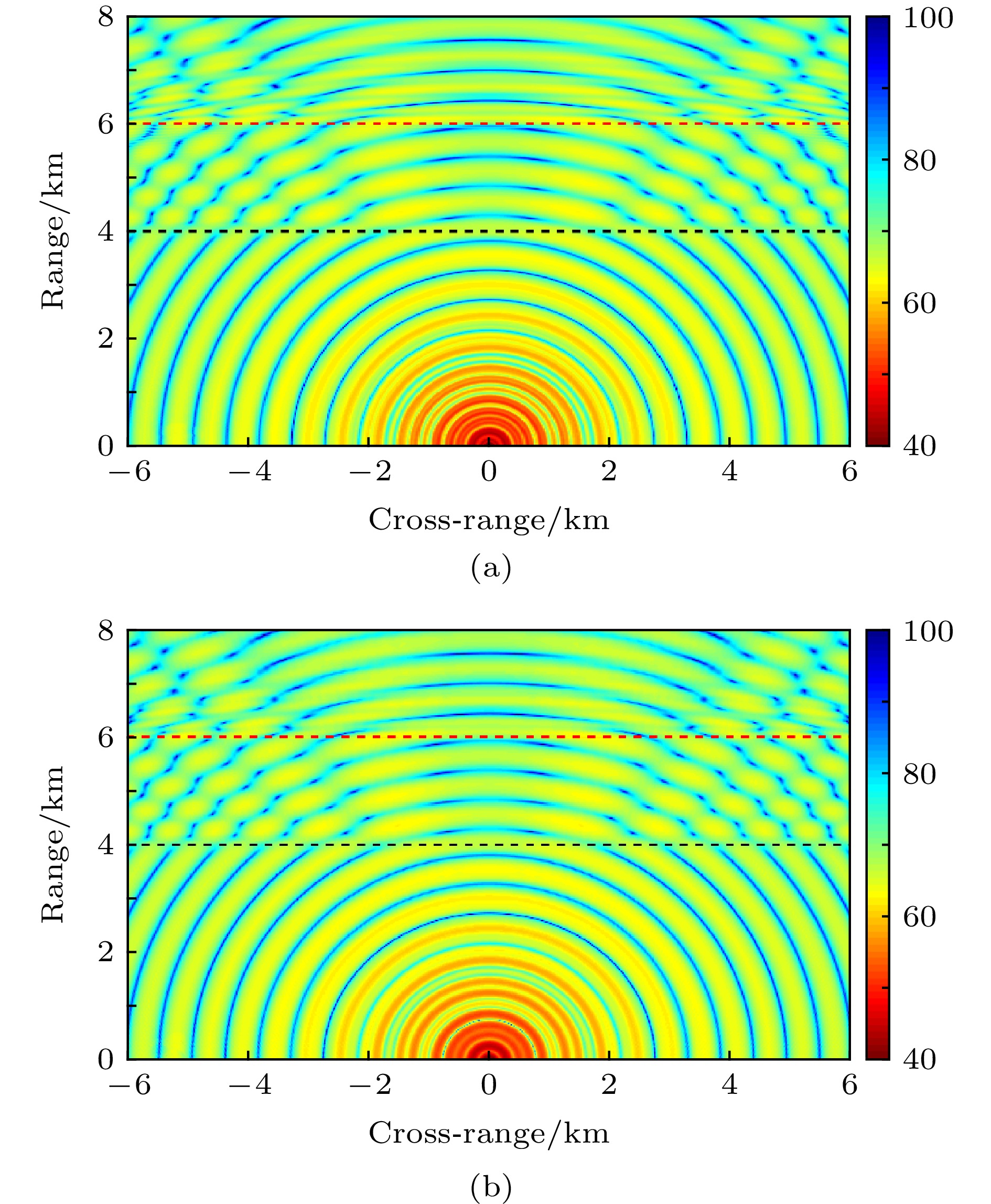
图 9 同时存在孤子内波和海脊时深度70 m水平平面上的三维传播损失 (a) DGMCM3D结果; (b)本文提出的三维模型的结果. 黑色和红色虚线分别表示孤子内波波包和海脊中心的位置
Figure 9. Three-dimensional transmission loss results in the horizontal plane at depth of 70 m in the presence of a solitary internal wave as well as a bottom ridge computed by (a) DGMCM3D and (b) the present 3D model. The center locations of the internal wave and the ridge are indicated by dashed black and red lines, respectively.
-
[1] 王宁, 张海青, 王好忠, 高大治 2010 声学学报 35 38
Wang N, Zhang H Q, Wang H Z, Gao D Z 2010 Acta Acust. 35 38
[2] 马树青, 杨士莪, 朴胜春, 李婷婷 2009 振动与冲击 28 73
Google Scholar
Ma S Q, Yang S E, Piao S C, Li T T 2009 J. Vib. Shock 28 73
Google Scholar
[3] Badiey M, Katsnelson B G, Lynch J F, Pereselkov S, Siegmann W L 2005 J. Acoust. Soc. Am. 117 613
Google Scholar
[4] Luo J, Badiey M, Karjadi E A, Katsnelson B, Tskhoidze A, Lynch J F, Moum J N 2008 J. Acoust. Soc. Am. 124 66
Google Scholar
[5] Lin Y T, Duda T F, Lynch J F 2009 J. Acoust. Soc. Am. 126 1752
Google Scholar
[6] Colosi J A 2008 J. Acoust. Soc. Am. 124 1452
Google Scholar
[7] Yang T C 2014 J. Acoust. Soc. Am. 135 610
Google Scholar
[8] Siegmann W L, Kriegsmann G A, Lee D 1985 J. Acoust. Soc. Am. 78 659
Google Scholar
[9] Lee D, Botseas G, Siegmann W L 1992 J. Acoust. Soc. Am. 91 3192
Google Scholar
[10] Collins M D, Chin-Bing S A 1990 J. Acoust. Soc. Am. 87 1104
Google Scholar
[11] Ferla C M, Porter M B, Jensen F B 1993 C-SNAP: Coupled SACLANTCEN Normal Mode Propagation Loss Model (La Spezia: SACLANT Undersea Research Center) pp1–46
[12] Luo W Y, Yang C M, Qin J X, Zhang R H 2012 Sci. Chin. Phys. Mech. Astron. 55 572
Google Scholar
[13] 杨春梅, 骆文于, 张仁和, 秦继兴 2014 声学学报 39 295
Yang C M, Luo W Y, Zhang R H, Qin J X 2014 Acta Acust. 39 295
[14] Luo W Y, Zhang R H 2015 Sci. China-G: Phys. Mech. Astron. 58 1
[15] Evans R B 1983 J. Acoust. Soc. Am. 74 188
Google Scholar
[16] Collins M D, Westwood E K 1991 J. Acoust. Soc. Am. 89 1068
Google Scholar
[17] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics （2nd ed.） (New York: Springer) pp337–445
[18] Buckingham M J 1989 J. Acoust. Soc. Am. 86 2273
Google Scholar
[19] Luo W Y, Yu X L, Yang X F, Zhang Z Z, Zhang R H 2016 Chin. Phys. B 25 124309
Google Scholar
[20] Jensen F B 1998 J. Acoust. Soc. Am. 104 1310
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8487
- PDF Downloads: 93
- Cited By: 0
