-
It is of great importance to investigate the dynamics of the multiple bubble system for revealing the mechanism of cavitation. Because of the secondary radiation of the oscillating bubbles, the coupled vibration of neighboring bubbles arises. Previous studies have reported that time delays appear to be more important when the coupled bubbles are close to each other. In this paper, we investigate the acoustical response of two bubble oscillators theoretically and numerically. Firstly, we modify the dynamic model equation by use of Taylor series being accurate up to terms of second order in radial displacement of bubbles. Based on the perturbation theory, the eigenmodes of the coupled-bubble system are analyzed, and two different resonant frequencies are obtained. Secondly, the effects of time delays on the coupled oscillation are analyzed numerically by use of phase diagram. When bubbles are driven by low-intensity ultrasound, we can neglect the effect of the time delay for the coupled-bubble system. Thirdly, the theoretical and numerical curve of amplitude versus frequency are compared with each other. There are two peaks on each curve on which present are two resonant regions. The relative position of the resonant peaks of the two bubbles in each region is similar for the two analytical methods. Finally, the effect of equivalent radius of bubble, equivalent radius ratio, bubble center distance, and driving pressure amplitude on the radial motion are numerically explored. With the increase of the intensity of the acoustic wave, the resonant peaks shift toward the low-frequency region. The coupled oscillation of the two bubbles of different radii could be intensified when these conditions are satisfied, such as resonant driving, equal radius, and the range of center distance smaller than 10R10. We can observe a transition phenomenon and out-of-phase fluctuation of the bubble oscillation in the strong coupling region. Therefore, bubbles play an important role of energy translator in the ultrasound applications.
[1] Ooi A, Nikolovska A, Manasseh R 2008 J. Acoust. Soc. Am. 124 815
Google Scholar
[2] Allen J S, Kruse D E, Dayton P A, Ferrara K W 2003 J. Acoust. Soc. Am. 114 1678
Google Scholar
[3] Mohd Y N S, Babgi B, Alghamdi Y, Aksu M, Madhavan J, Ashokkumar M 2016 Ultrason. Sonochem. 29 568
Google Scholar
[4] Ashokkumar M 2011 Ultrason. Sonochem. 18 864
Google Scholar
[5] Prosperetti A, Crum L A, Commander K W 1988 J. Acoust. Soc. Am. 83 502
Google Scholar
[6] Wang C H, Cheng J C 2013 Chin. Phys. B 22 014304
Google Scholar
[7] Zhang Y N, Li S C 2016 Ultrason. Sonochem. 29 129
Google Scholar
[8] Doinikov A A 2004 J. Acoust. Soc. Am. 116 821
Google Scholar
[9] Yasui K, Lee J, Tuziuti T, Towata A, Kozuka T, Yasuo I 2009 J. Acoust. Soc. Am. 126 973
Google Scholar
[10] Hegedus F, Klapcsik K 2015 Ultrason. Sonochem. 27 153
Google Scholar
[11] 胡静, 林书玉, 王成会, 李锦 2013 62 114301
Google Scholar
Hu J, Lin S Y, Wang C H, Li J 2013 Acta Phys. Sin. 62 114301
Google Scholar
[12] Takahira H, Yamane S, Akamatsu T 1995 JSME Int. J. Ser. B 38 432
Google Scholar
[13] Naohiro S, Keita A, Toshihiko S 2017 Ultrasonics 77 160
Google Scholar
[14] Chew L W, Klaseboer E, Ohl S W, Khoo B C 2011 Phys. Rev. E 84 066307
Google Scholar
[15] Versluis M, Schmitz B, Heydt A V D, Lohse D 2000 Science 289 2114
Google Scholar
[16] Masato I 2009 Phys. Rev. E 79 016307
Google Scholar
[17] Jiang L, Liu F B, Chen H S, Wang J D, Chen D R 2012 Phys. Rev. E 85 036312
Google Scholar
[18] Bonabi R S, Rezaee N, Ebrahimi H, Mirheydari M 2010 Phys. Rev. E 82 016316
Google Scholar
[19] Masato I 2007 Phys. Rev. E 76 046309
Google Scholar
[20] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[21] Doinikov A A, Manasseh R, Ooi A 2005 J. Acoust. Soc. Am. 117 47
Google Scholar
[22] Sugita N, Toshihiko S 2017 Ultrasonics 74 174
Google Scholar
[23] Ikeda T, Harata Y, Hiraoka R 2015 Nonlinear Dyn. 81 1759
Google Scholar
[24] Dzaharudin F, Suslov S A, Manasseh R, Ooi A 2013 J. Acoust. Soc. Am. 134 3425
Google Scholar
-
图 1 驱动压力幅值分别为1.5, 1.0和0.5 atm时气泡径向振动相图 其中图 (a)−(c)为气泡1的振动相图, 图(d)−(f)为气泡2的振动相图
Figure 1. Radial vibration phase diagram at 1.5, 1.0, 0.5 atm driving pressure amplitude for bubble 1 (a)−(c) and bubble 2 (d)−(f).
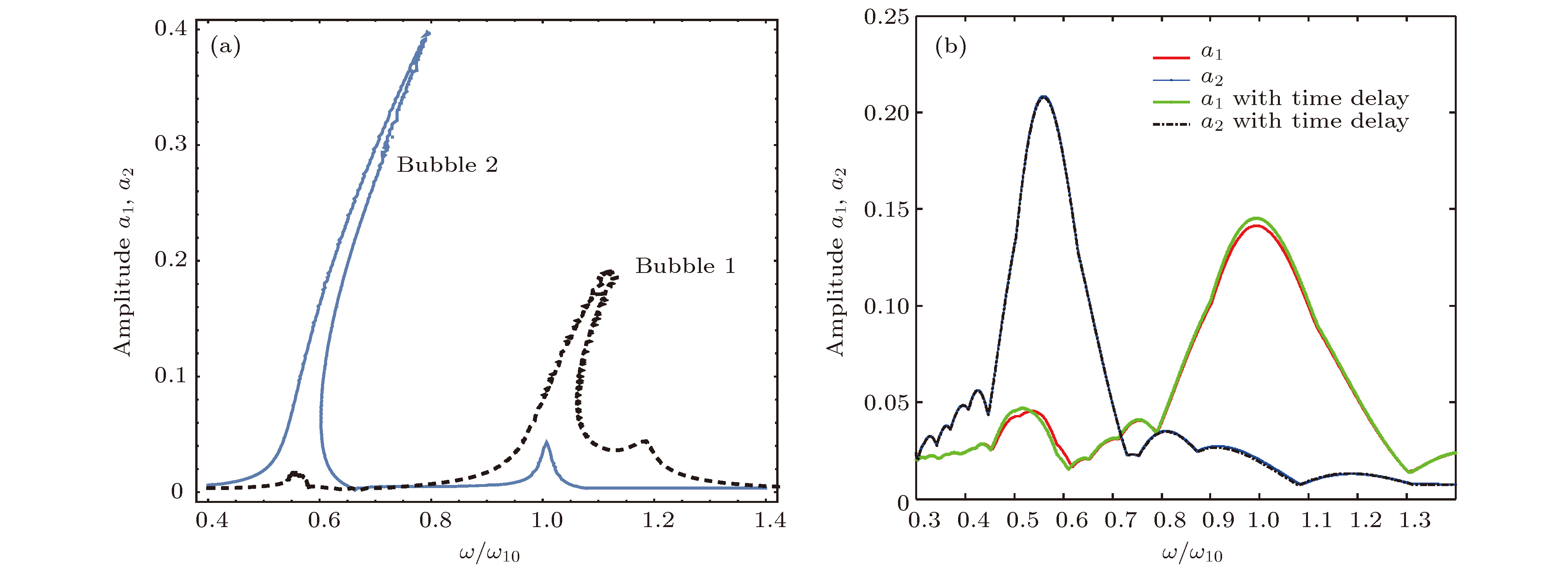
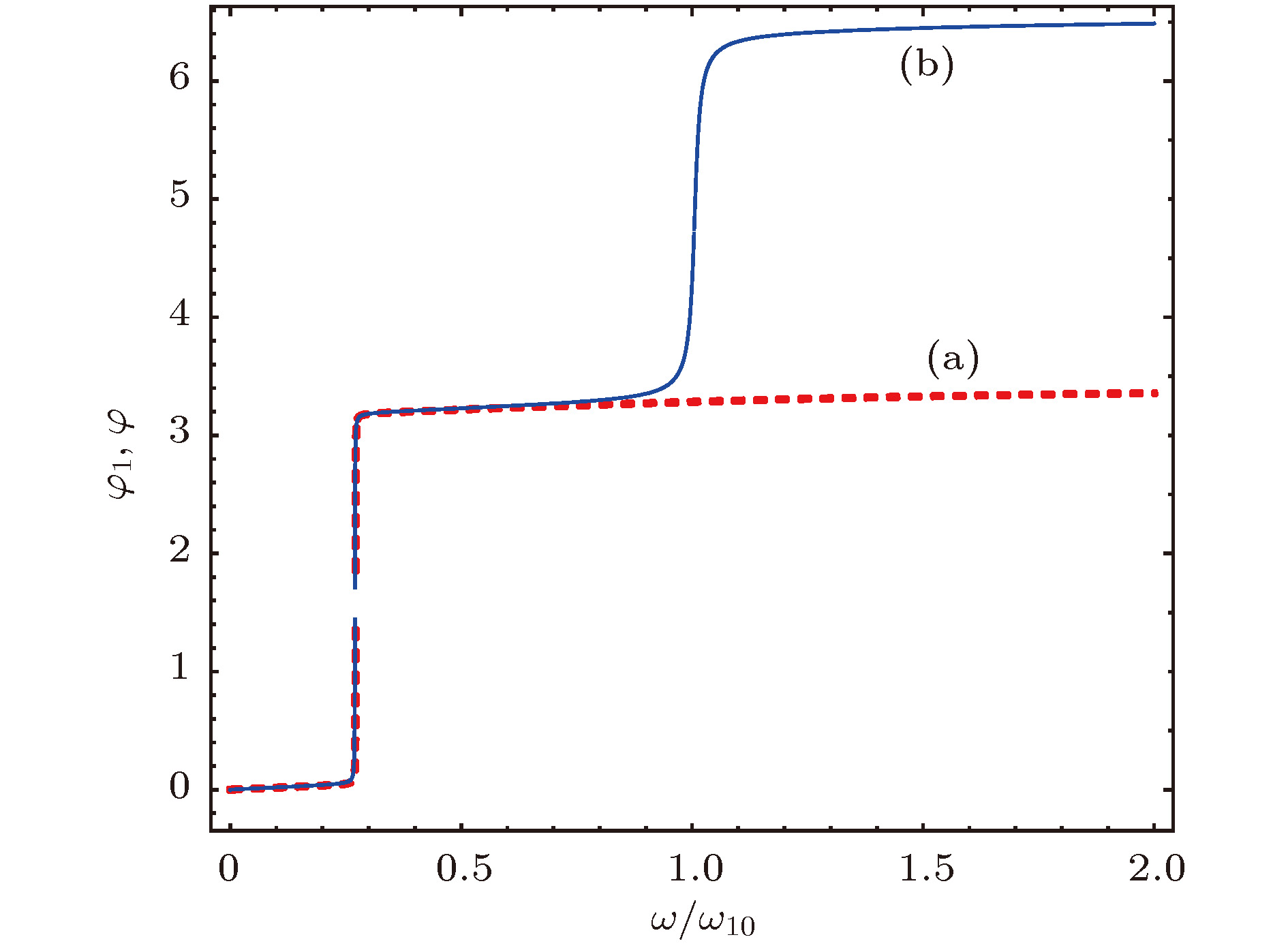
图 2 气泡振动幅值-驱动频率响应关系对比 (a) 理论分析; (b) 数值分析(bubble 1, 3 μm, bubble 2, 5 μm, 驱动声波压力幅值pa = 0.1 atm)
Figure 2. Comparison the responding relationship between vibration amplitude and driving frequency: (a) Theoretical analysis; (b) numerical analysis, where the diameter of the bubble 1 is 3 μm and the bubble 2 is 5 μm, the amplitude of driving pressure is pa = 0.1 atm
图 3 气泡振动幅值与驱动频率的关系 (a) pa = 0.5 atm; (b) pa = 1 atm (bubble 1, 3 μm; bubble 2, 5 μm)
Figure 3. Vibration amplitude vs. driving frequency: (a) pa = 0. 5 atm; (b) pa = 1 atm, where the diameter of the bubble 1 is 3 μm, the bubble 2 is 5 μm.
图 4 气泡振动幅值随初始半径变化曲线 (a)气泡1; (b)气泡2
Figure 4. Curves of vibration amplitude with initial radius: (a) Bubble 1, (b) bubble 2.
图 5 气泡间距对气泡声响应的影响
Figure 5. Influence of bubble distance on sound response of bubbles.
图 6 气泡平衡半径比的影响
Figure 6. Influence of bubble equilibrium radius ratio.
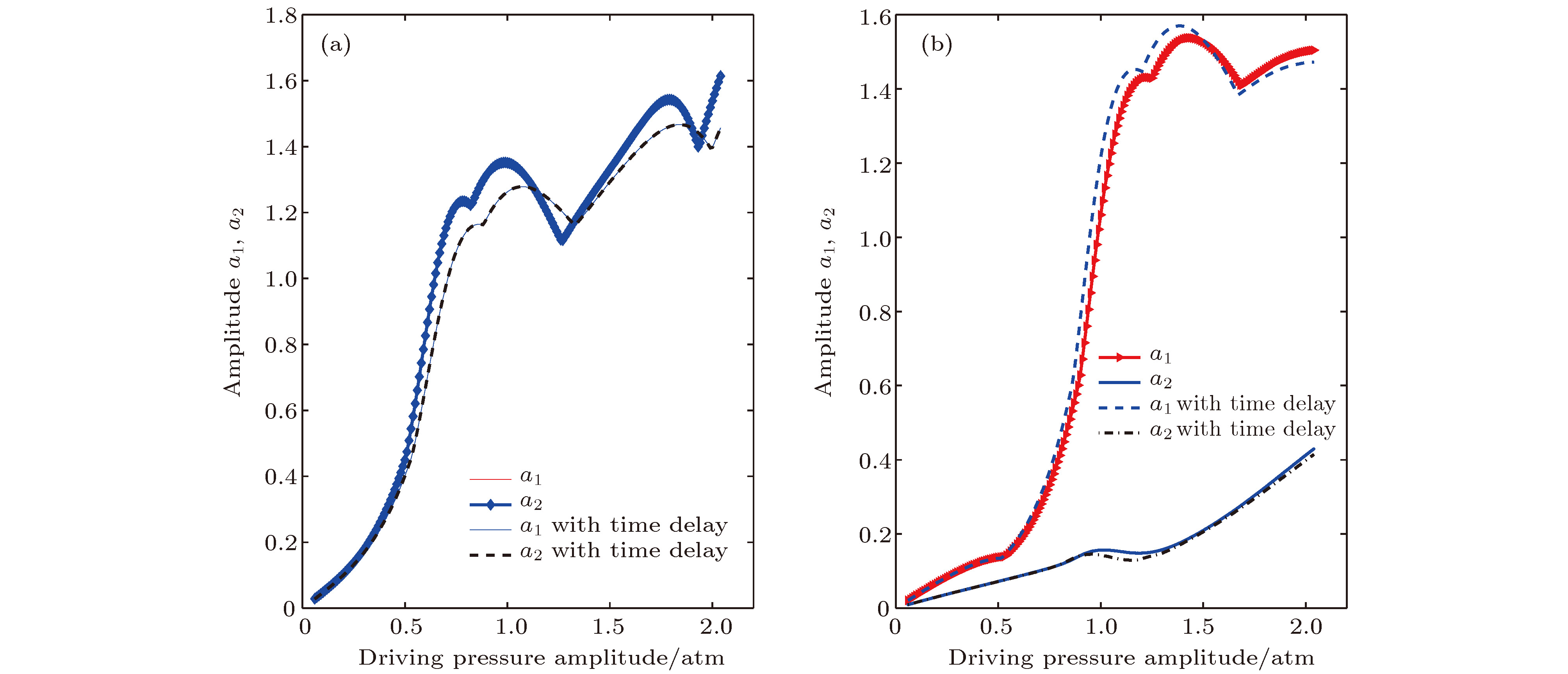
图 7 驱动压力影响 (a)
${R_{10}} = {R_{20}} = {\rm{3 \;{\text{μ}}m}}$ ; (b)${R_{10}} = {\rm{3 \;{\text{μ}}m}}$ ,${R_{20}} = {\rm{5\;{\text{μ}}m}}$ Figure 7. Effects of driving pressure: (a)
${R_{10}} = {R_{20}} = {\rm{3\; {\text{μ}}m}}$ ; (b)${R_{10}} = \;{\rm{3\; {\text{μ}}m}}$ ,${R_{20}} = {\rm{5 \;{\text{μ}}m}}$ .
图 8 气泡振动相位随频率变化 (a)
${R_{10}} = {\rm{3 \;{\text{μ}}m}}$ 气泡初相位φ1; (b)驱动力振动初相位φFigure 8. Oscillation phase varies with frequency: (a) Initial phase φ1 of
${R_{10}} = {\rm{3 \;{\text{μ}}m}}$ ; (b) initial phase φ of driving force. -
[1] Ooi A, Nikolovska A, Manasseh R 2008 J. Acoust. Soc. Am. 124 815
Google Scholar
[2] Allen J S, Kruse D E, Dayton P A, Ferrara K W 2003 J. Acoust. Soc. Am. 114 1678
Google Scholar
[3] Mohd Y N S, Babgi B, Alghamdi Y, Aksu M, Madhavan J, Ashokkumar M 2016 Ultrason. Sonochem. 29 568
Google Scholar
[4] Ashokkumar M 2011 Ultrason. Sonochem. 18 864
Google Scholar
[5] Prosperetti A, Crum L A, Commander K W 1988 J. Acoust. Soc. Am. 83 502
Google Scholar
[6] Wang C H, Cheng J C 2013 Chin. Phys. B 22 014304
Google Scholar
[7] Zhang Y N, Li S C 2016 Ultrason. Sonochem. 29 129
Google Scholar
[8] Doinikov A A 2004 J. Acoust. Soc. Am. 116 821
Google Scholar
[9] Yasui K, Lee J, Tuziuti T, Towata A, Kozuka T, Yasuo I 2009 J. Acoust. Soc. Am. 126 973
Google Scholar
[10] Hegedus F, Klapcsik K 2015 Ultrason. Sonochem. 27 153
Google Scholar
[11] 胡静, 林书玉, 王成会, 李锦 2013 62 114301
Google Scholar
Hu J, Lin S Y, Wang C H, Li J 2013 Acta Phys. Sin. 62 114301
Google Scholar
[12] Takahira H, Yamane S, Akamatsu T 1995 JSME Int. J. Ser. B 38 432
Google Scholar
[13] Naohiro S, Keita A, Toshihiko S 2017 Ultrasonics 77 160
Google Scholar
[14] Chew L W, Klaseboer E, Ohl S W, Khoo B C 2011 Phys. Rev. E 84 066307
Google Scholar
[15] Versluis M, Schmitz B, Heydt A V D, Lohse D 2000 Science 289 2114
Google Scholar
[16] Masato I 2009 Phys. Rev. E 79 016307
Google Scholar
[17] Jiang L, Liu F B, Chen H S, Wang J D, Chen D R 2012 Phys. Rev. E 85 036312
Google Scholar
[18] Bonabi R S, Rezaee N, Ebrahimi H, Mirheydari M 2010 Phys. Rev. E 82 016316
Google Scholar
[19] Masato I 2007 Phys. Rev. E 76 046309
Google Scholar
[20] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[21] Doinikov A A, Manasseh R, Ooi A 2005 J. Acoust. Soc. Am. 117 47
Google Scholar
[22] Sugita N, Toshihiko S 2017 Ultrasonics 74 174
Google Scholar
[23] Ikeda T, Harata Y, Hiraoka R 2015 Nonlinear Dyn. 81 1759
Google Scholar
[24] Dzaharudin F, Suslov S A, Manasseh R, Ooi A 2013 J. Acoust. Soc. Am. 134 3425
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6933
- PDF Downloads: 78
- Cited By: 0
