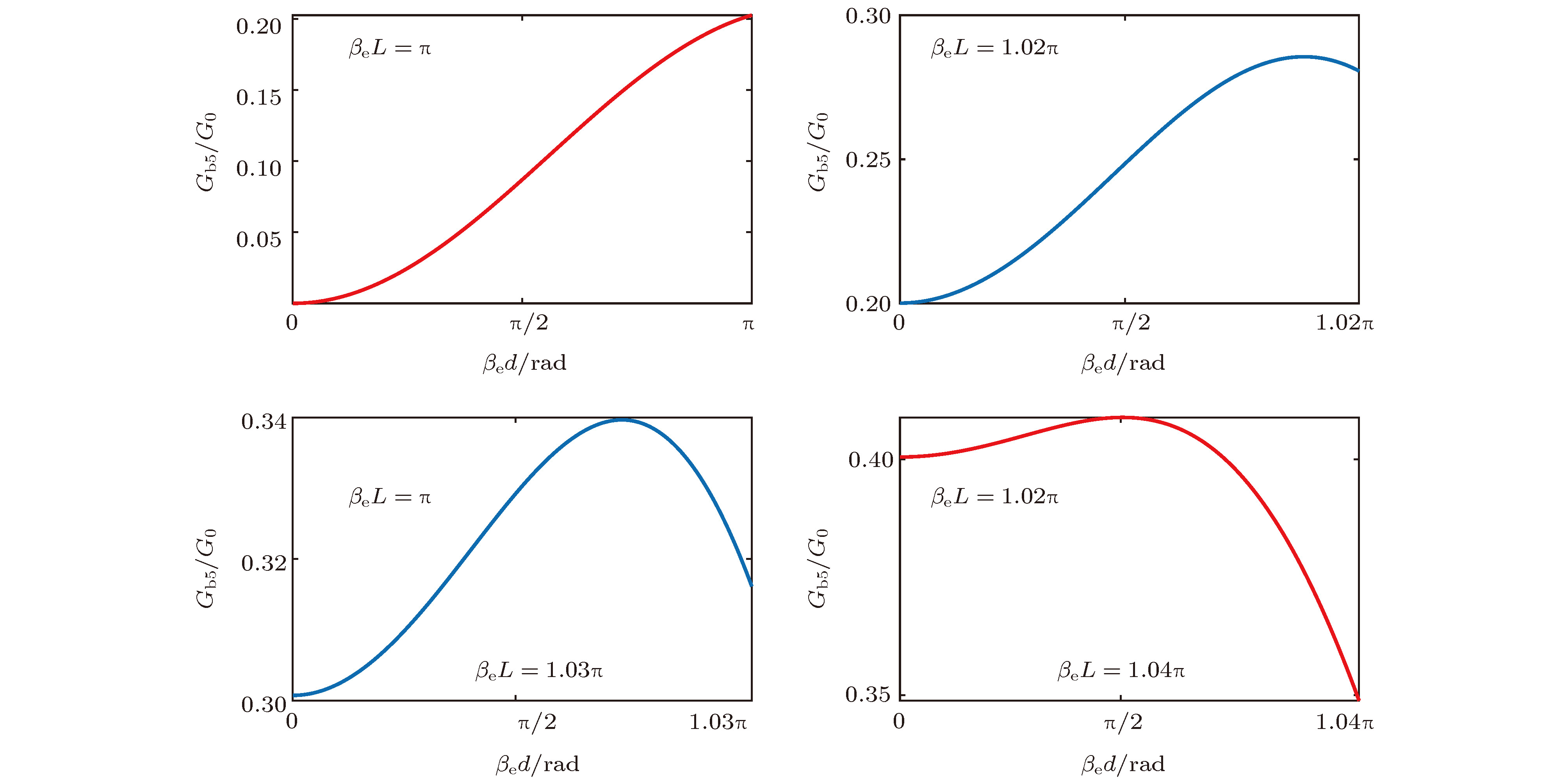
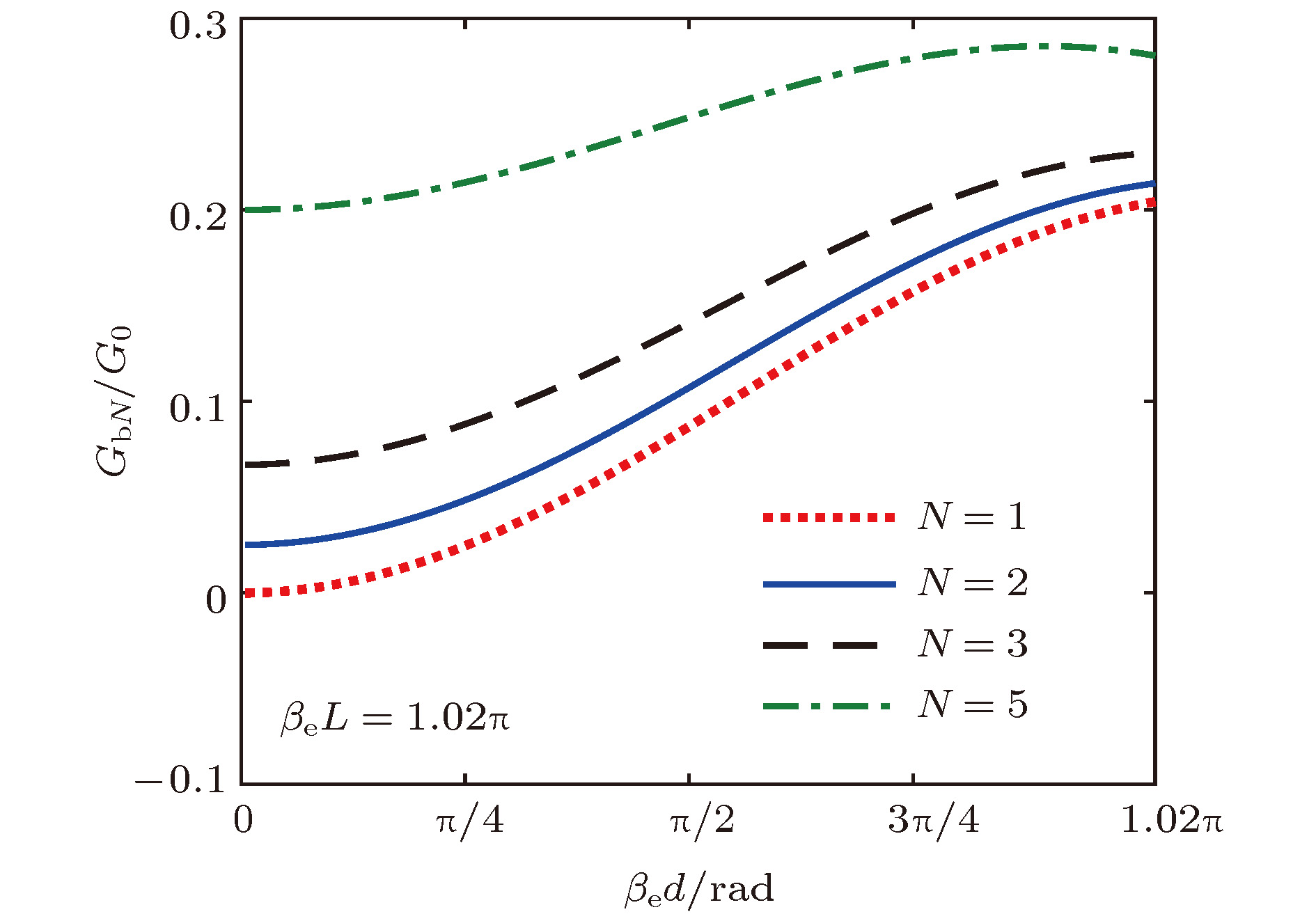
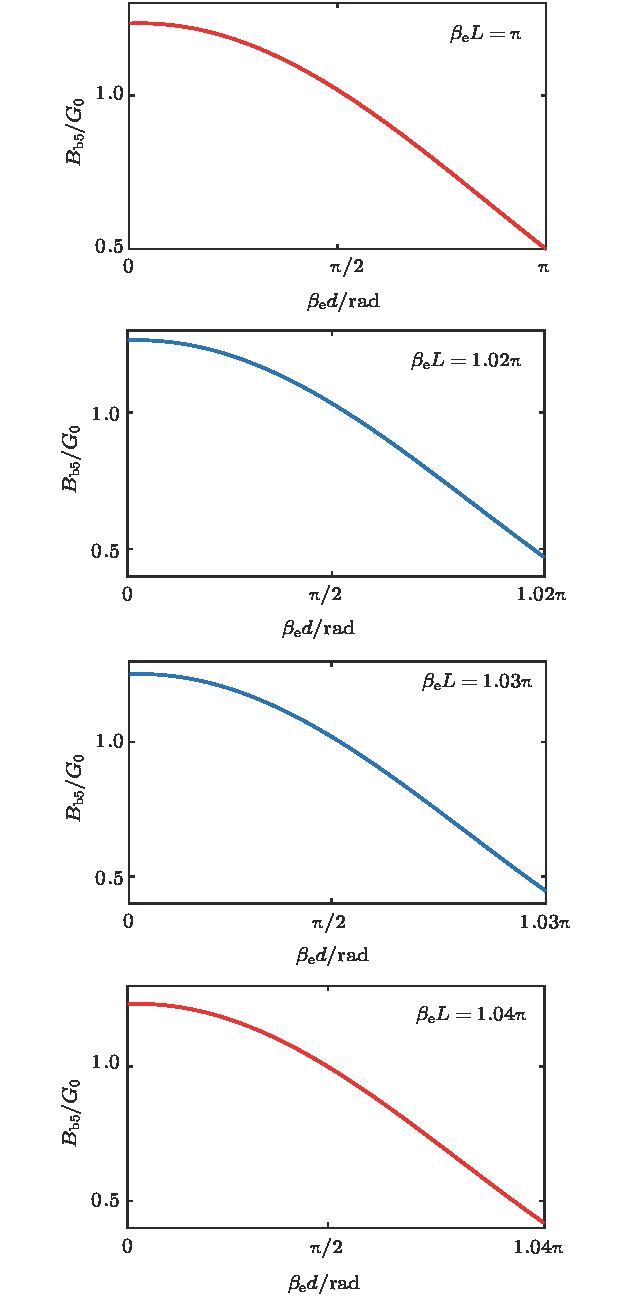
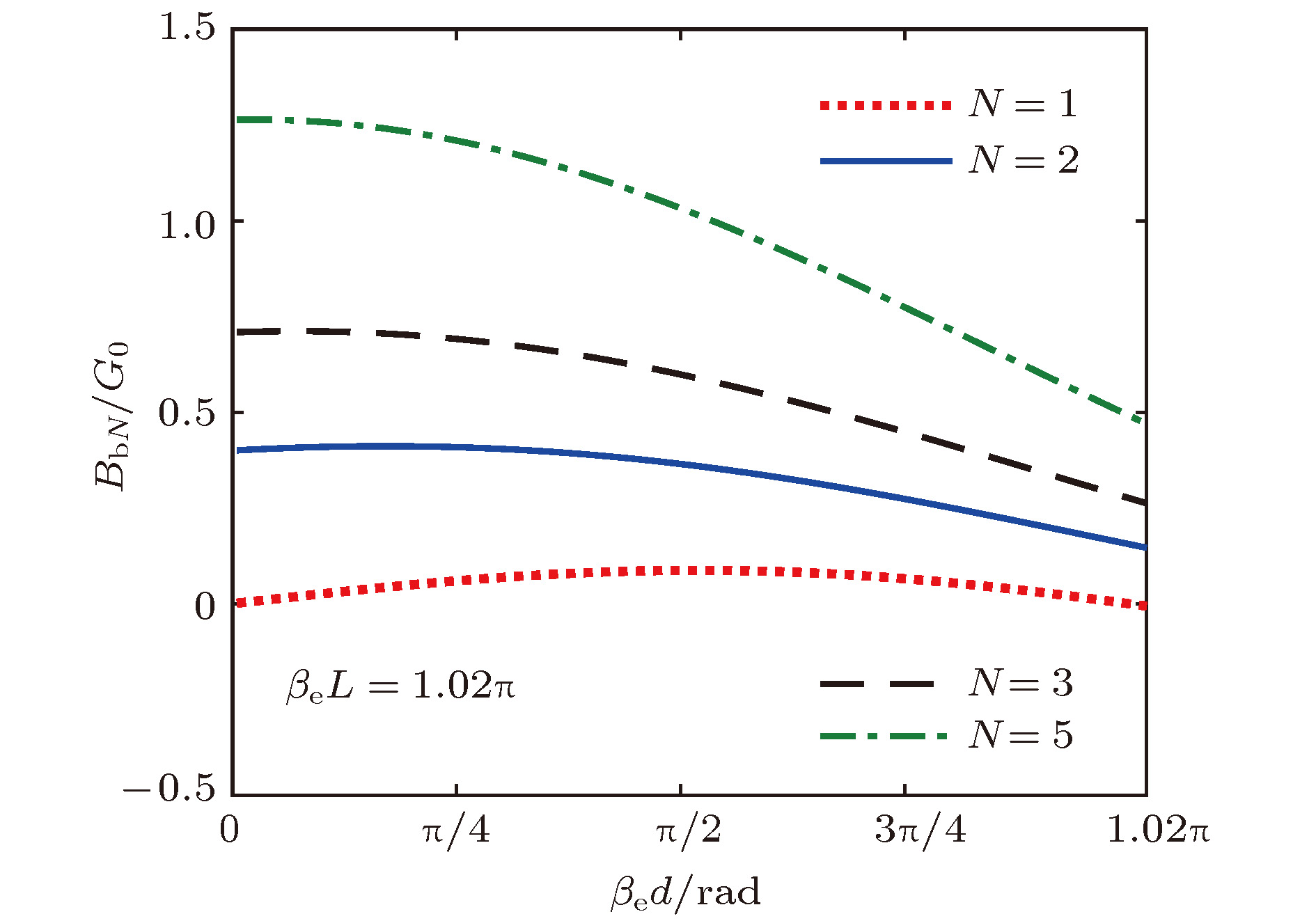
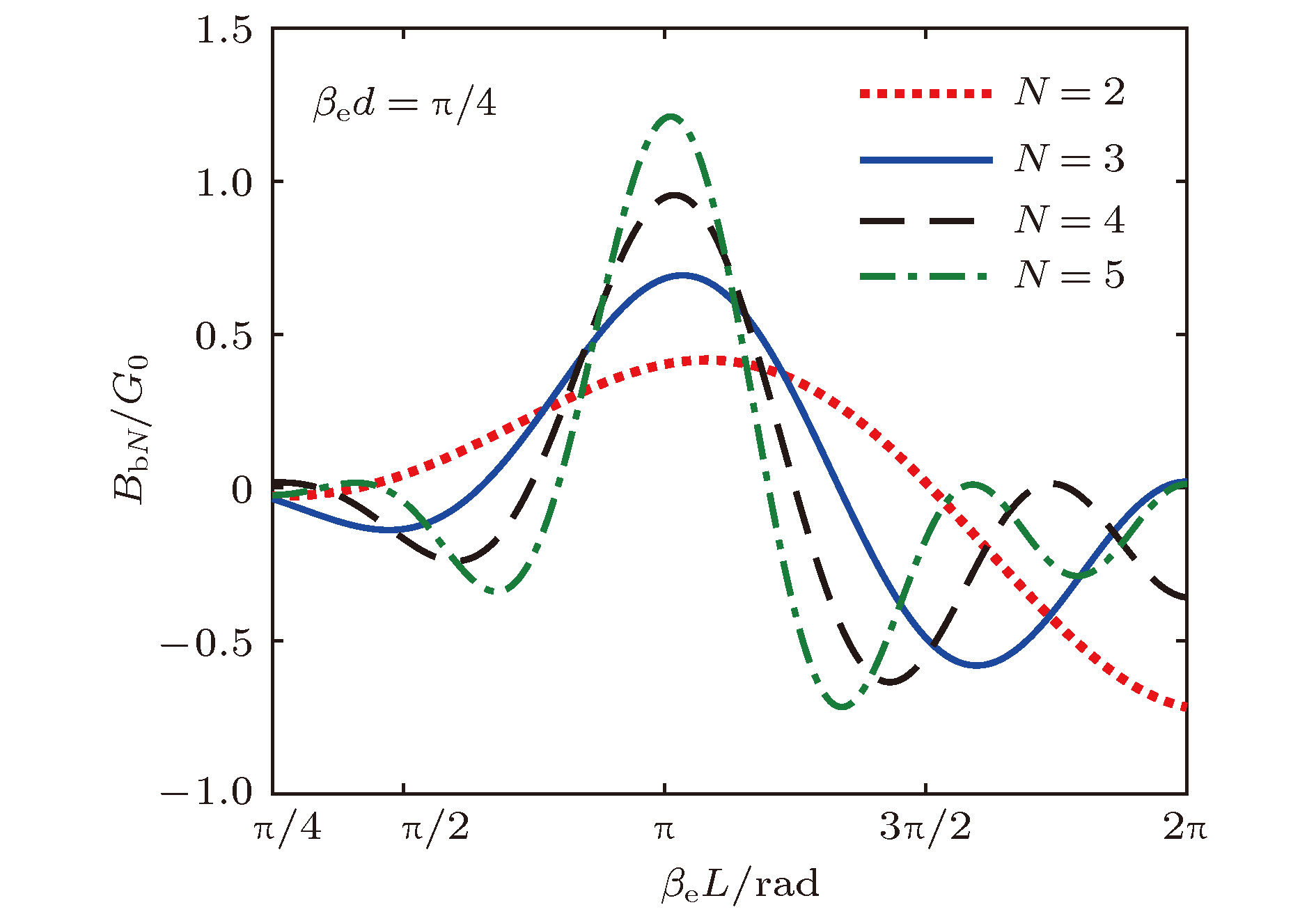
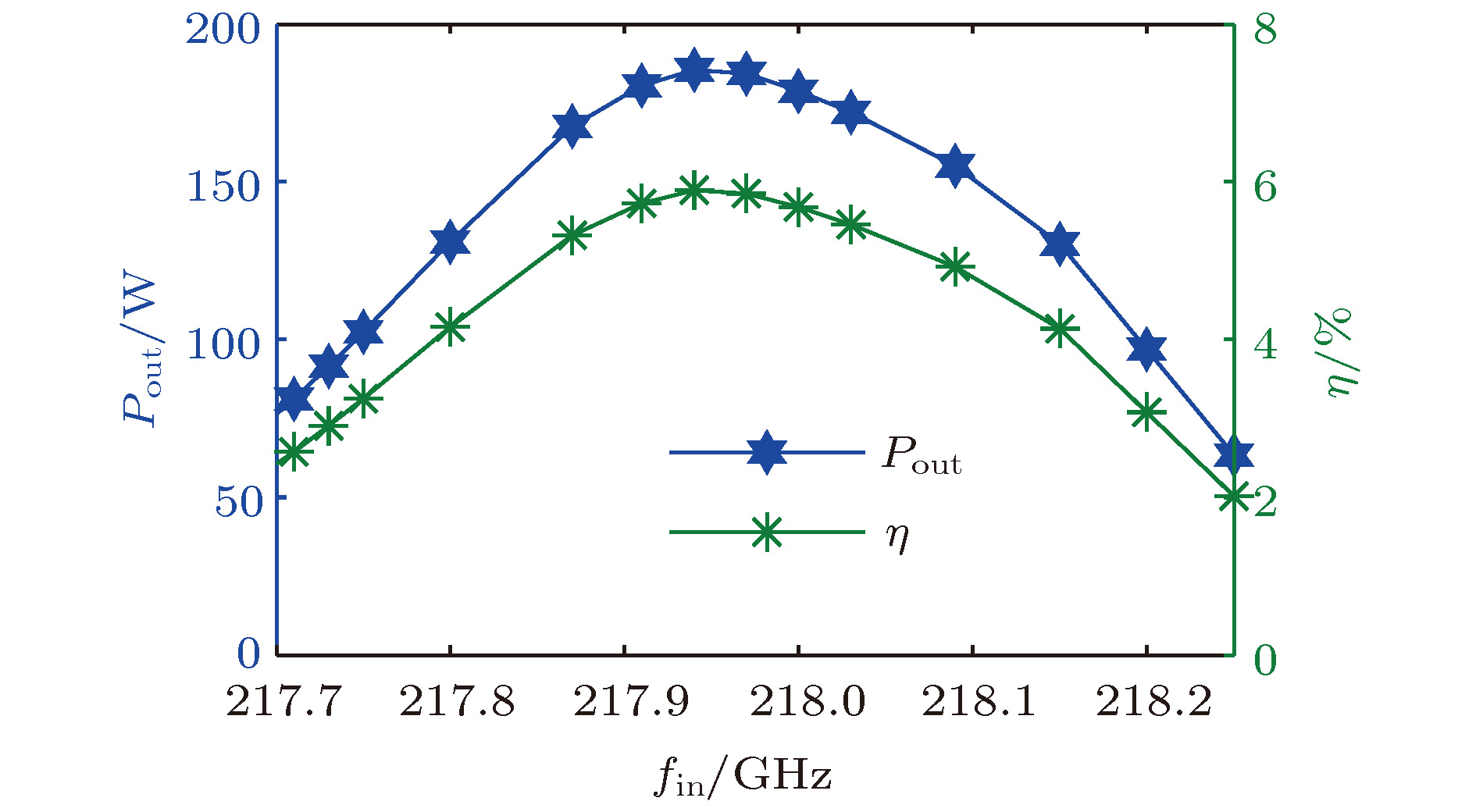
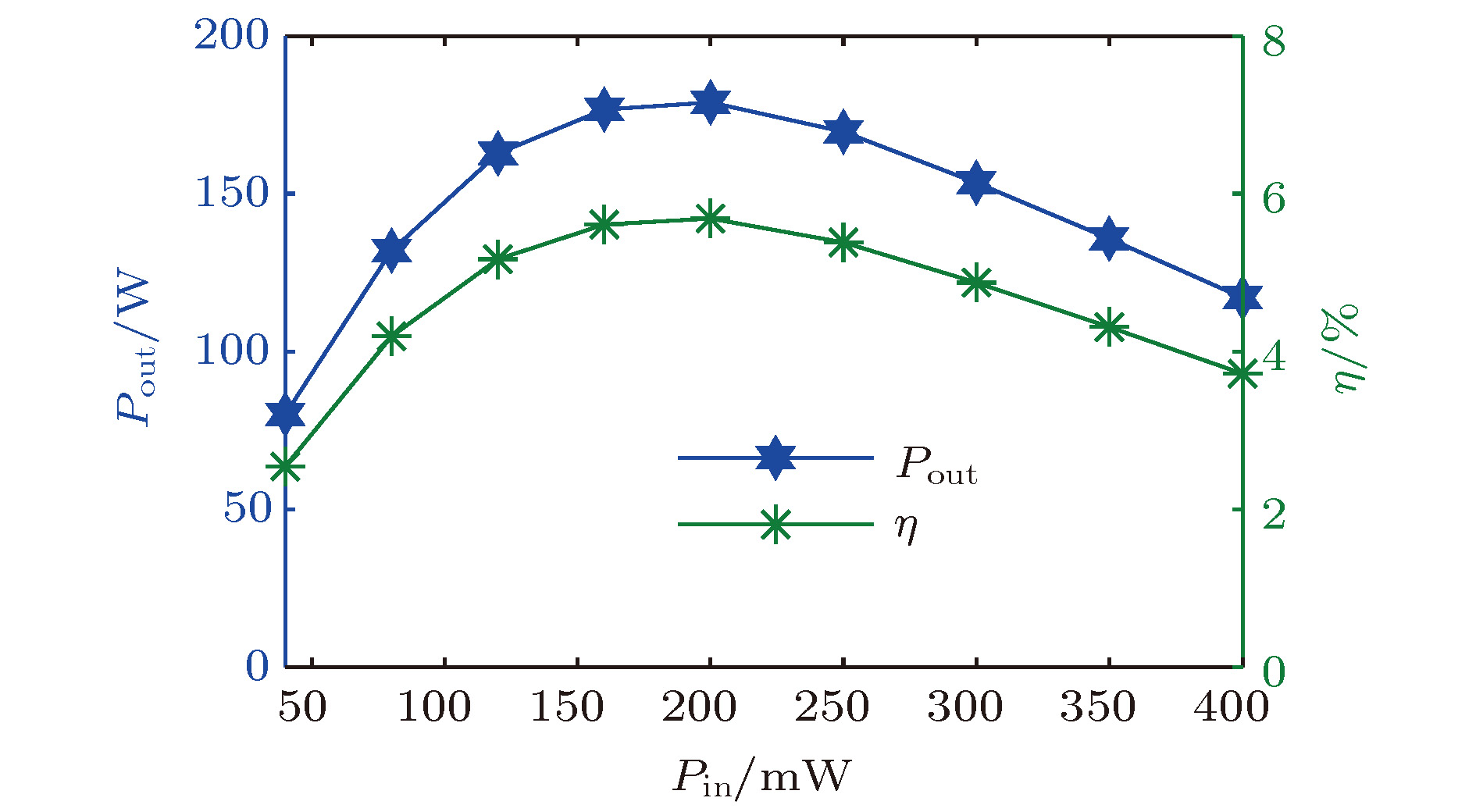
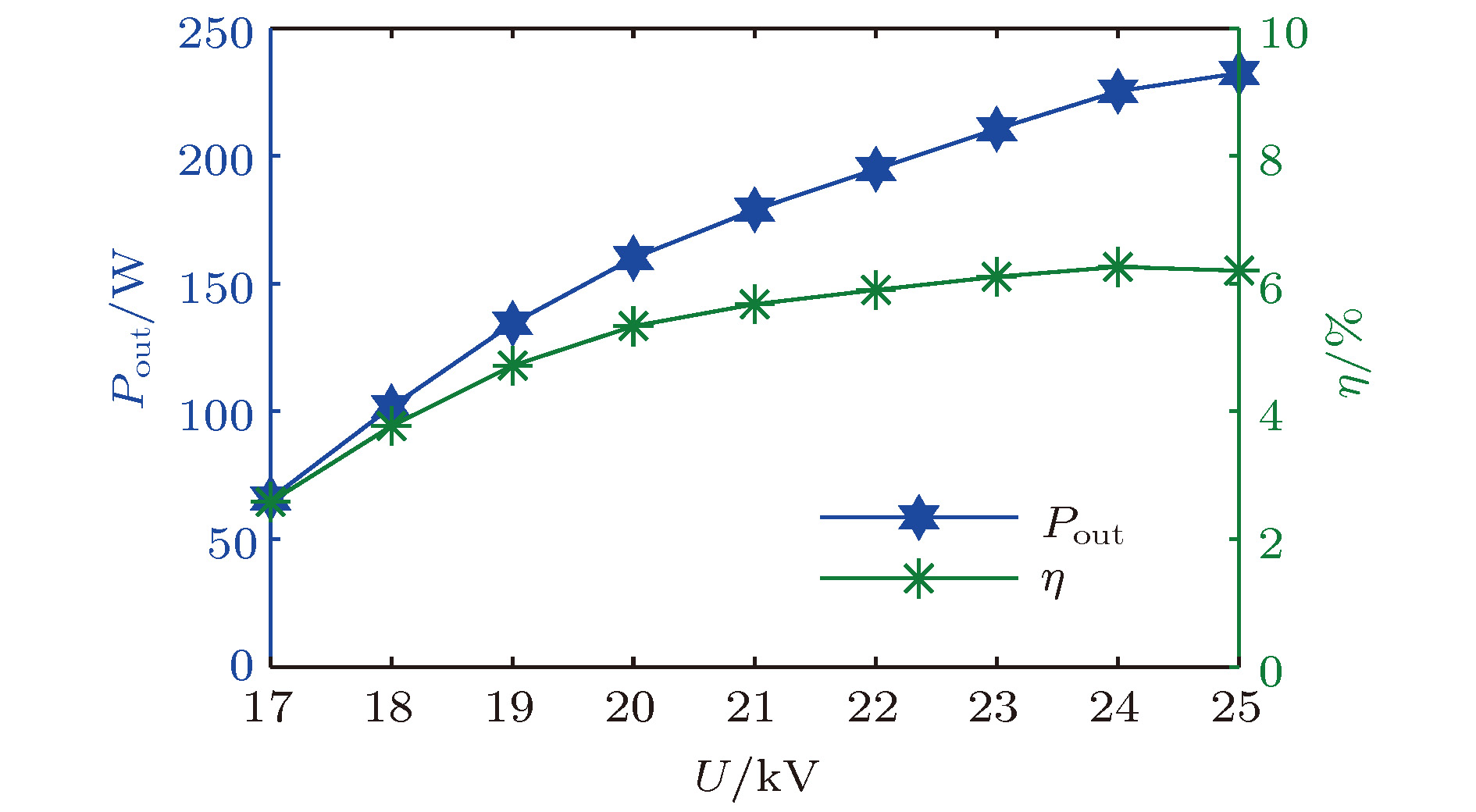
-
Extended interaction klystron is a very important millimeter-wave and sub-millimeter-wave vacuum electron device with many actual and potential applications, such as space-borne cloud profiling radar, communication, imaging system, precision guided missiles, etc. Kinematical theory and space charge wave theory are extensively used to analyze the bunching process of electrons. Kinematical theory is precise when electron beam is especially small because the influence of space charge effect is ignored, while space charge wave theory is accurate when the modulation of electron beam is small since it is based on the premise of small amplitude. Based on kinematical theory, law of induce current, principle of charge conservation in a one-dimensioanl mode and small signal condition, the influence of electron beam on standing wave electric field in multiple-gap cavity is analyzed, and the expression of beam-loading conductance and beam-loading susceptance in multiple-gap cavity are derived. The influence of the direct current transmit angle of single gap, the number of multiple gaps and the direct current transmit angle of between center of adjacent gaps on beam-loading conductance and beam-loading susceptance are analyzed. The results show that the beam-loading conductance and beam-loading susceptance of multiple-gap cavity can change to a bigger extent when the number of cavity gaps is bigger, which means that the maximum beam-wave conversion efficiency and the range of loaded frequency increase with the number of cavity gaps increasing. The results also show that the direct current transmit angle between centers of adjacent gaps is the most important parameter for the beam-wave interaction effect. Based on the above analysis, a G-band extended interaction klystron amplifier consisting of three five-gap cavities is designed by an three-dimensional PIC code. An output power of 225.5 W at 217.94 GHz with an efficiency of 6.26%, whose gain and 3 dB bandwidth are 30.5 dB and 470 MHz respectively, is obtained by simulation. This study is of great significance for the physical design and process in engineering the G-band extended interaction klystron amplifier.
-
Keywords:
- G-band /
- extended interaction klystron /
- beam-wave interaction /
- beam loading
[1] 刘振帮, 赵欲聪, 黄华, 金晓, 雷禄容 2015 64 108404
Google Scholar
Liu Z B, Zhao Y C, Huang H, Jin X, Lei L R 2015 Acta Phys. Sin. 64 108404
Google Scholar
[2] Gutiérrez J, Pascual J P, Tazón A 2018 Int. J. RF Microwave Comput. Aided Eng. 28 21284
Google Scholar
[3] Rhoads C, Goshi D S 2018 IEEE Radar Conference Oklahoma, USA, April 23−27, 2018 p0344
[4] 刘国, 王建勋, 罗勇 2013 62 078404
Google Scholar
Liu G, Wang J X, Luo Y 2013 Acta Phys. Sin. 62 078404
Google Scholar
[5] 陈姝媛, 阮存军, 王勇, 张长青, 钟勇, 赵鼎 2015 红外与毫米波学报 34 230
Google Scholar
Chen S Y, Ruan C J, Wang Y, Zhang C Q, Zhong Y, Zhao D 2015 J. Infrared Millmeter Waves 34 230
Google Scholar
[6] Feng J J, Cai J, Hu Y F, Wu X P, Du Y H, Liu J K, Pan P, Li H Y 2014 IEEE Trans. Electron Dev. 61 1721
Google Scholar
[7] Gerum W, Lippert G, Malzahn P, Schneider K 2001 IEEE Trans. Electron Dev. 48 72
Google Scholar
[8] Richard K, Andrew Z, Clark M, Mike M, Mark K, Richard T, Ai T, John R, Carter A 2013 IEEE International Vacuum Electronics Conference Paris, France, May 21−23, 2013 p1
[9] 吴洋, 许州, 周霖, 李文君, 唐传祥 2012 61 224101
Google Scholar
Wu Y, Xu Z, Zhou L, Li W J, Tang C X 2012 Acta Phys. Sin. 61 224101
Google Scholar
[10] Maslennikov S P, Paramonov Y N, Serebryakova A S 2018 IEEE International Vacuum Electronics Conference Monterey, USA, April 24−26, 2018 p215
[11] She J C, Huang Z Z, Huang Y F, Huang Z J, Chen J, Deng S Z, Xu N S 2017 International Vacuum Nanoelectronics Conference, Regensburg Germany, July 10−14, 2017 p4
[12] Li R J, Ruan C J, Zhang H F 2018 Phys. Plasmas 25 033107
Google Scholar
[13] Toreev A I, Fedorov V K, Patrusheva E V 2009 J. Commun. Technol. Electron. 54 952
Google Scholar
[14] Dave B, Henry D, Richard D, Peter H, Mark H, Andrew K, Ross M, Albert R, Ed S, Brian S 2014 IEEE Trans. Electron Devices 61 1830
Google Scholar
[15] Chang Z W, Meng L, Yin Y, Wang B, Li H L, Rauf A, Ullah S, Bi L J, Peng R B 2018 IEEE Trans. Electron Dev. 65 1179
Google Scholar
[16] Qu Z W, Zhang Z Q, Ding Y G, Wang S Z, Li Q S 2018 IEEE International Vacuum Electronics Conference Monterey, USA, April 24−26, 2018 p189
[17] Albert R, Dave B, Brian S 2018 IEEE Trans. Electron Dev. 52 895
[18] Brian S, Albert R, Peter H, Mark H, Richard D, Dave B 2011 Proceedings of the 41st European Microwave Conference Manchester, UK, Oct 10−13, 2011 p984
[19] Hu L L, Zeng Z J, Chen H B, Ma G W, Meng F B 2018 J. Eng. 2018 689
[20] Li R J, Ruan C J 2017 IEEE International Vacuum Electronics Conference London, UK, April 24−26, 2017 p1
[21] Li S F, Duan Z Y, Wang F, Wang Z L, Xu J, Gong Y B 2014 Int. Conf. Infrared, Millim., Terahertz Waves, Tucson, USA, September 14−19, 2014 p2
[22] Zhong Y, Liu W X, Wang Y, Ruan C J, Wang S Z 2012 Int. Conf. Infrared, Millim., Terahertz Waves Wollongong, Australia, September 23−28, 2012 p1
[23] 盛兴, 韦莹, 孙福江, 王瑞海, 冯海平, 胡晓斌 2012 真空电子技术 2 19
Google Scholar
Sheng X, Wei Y, Sun F J, Wang R H, Feng H P, Hu X B 2012 Vacuum Electronics 2 19
Google Scholar
[24] 曾造金 2014 硕士学位论文 (成都: 电子科技大学)
Zeng Z J 2014 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[25] 谢家麟, 赵永翔 1966 速调管群聚理论 (北京: 科学出版社) 第33−177页
Xie J L, Zhao Y X 1966 Bunching Theory of Klystron (Beijing: Science Press) pp33−177 (in Chinese)
[26] 丁耀根 2008 大功率速调管的理论与计算模拟 (北京: 国防工业出版社) 第44−75页
Ding Y G 2008 Theory and Computer Simulation of High Power Klystron (Beijing: National Defense Industry Press) pp44−75 (in Chinese)
[27] Zhao Y C, Li S F, Huang H, Liu Z B, Wang Z L, Dan Z Y, Li X Y, Wei Y Y, Gong Y B 2015 IEEE Trans. Plasma Sci. 43 1862
Google Scholar
[28] 范植开, 刘庆想, 刘锡三, 周传民, 胡海膺 1999 强激光与粒子束 11 633
Fan Z K, Liu Q X, Liu X S, Zhou C M, Hu H Y 1999 High Power Laser and Particle Beams 11 633
[29] Lemke R W, Clark M C, Marder B M 1994 J. Appl. Phys. 75 10
[30] 范植开, 刘庆想, 刘锡三, 何琥, 周传民 1999 强激光与粒子束 11 482
Fan Z K, Liu Q X, Liu X S, He H, Zhou C M 1999 High Power Laser and Particle Beams 11 482
[31] Marcum J 1946 J. Appl. Phys. 17 4
Google Scholar
[32] Marder B M, Clark M C, Bacon L D, Hoffman J M, Lemke R W, Coleman P D 1992 IEEE Trans. Plasma Sci. 20 312
Google Scholar
[33] Carlsten B E, Haynes W B 1996 IEEE Trans. Plasma Sci. 24 1249
Google Scholar
[34] 范植开 1999 博士学位论文(北京: 中国工程物理研究院)
Fan Z K 1999 Ph. D. Dissertation (Beijing: China Academy of Engineering Physics) (in Chinese)
[35] 哈依柯夫 著 (黄高年 译) 1980 速调管放大器 (北京: 国防工业出版社) 第92, 93页
Eckertova L (translated by Hang G N) 1980 Клиотронные усилители (Beijing: National Defense Industry Press) pp92, 93 (in Chinese)
[36] Zhang Z H, Shu T, Zhang J, Qi Z M, Zhu J 2012 IEEE Trans. Plasma Sci. 40 3121
Google Scholar
[37] 徐翱, 周泉丰, 阎磊, 陈洪斌 2013 强激光与粒子束 25 2954
Xu A, Zhou Q F, Yan L, Chen H B 2013 High Power Laser and Particle Beams 25 2954
[38] Hsu H L 2006 Ph. D. Dissertation (Davis: University of California)
-
图 1 引入电子注后谐振腔等效电路
Figure 1. Equivalent circuit mode of cavity with beam.
图 2 多间隙谐振腔
${\text{π}}$ 模场简化示意图Figure 2. Simplified E-field of
${\text{π}}$ mode in multiple-gap cavity.
图 3 五间隙数谐振器的归一化电子负载电导与渡越角的关系
Figure 3. Gb5/G0 versus θ0 of five-gap cavity.
图 4 五间隙数谐振器的归一化电子负载电导与βeL的关系
Figure 4. Gb5/G0 versus βeL of five-gap cavity.
图 5 不同间隙数谐振器的归一化电子负载电导与渡越角的关系
Figure 5. GbN/G0 versus θ0 of multiple-gap cavity.
图 6 不同间隙数谐振器的归一化电子负载电导与渡越角的关系
Figure 6. GbN/G0 versus θ0 of multiple-gap cavity.
图 7 五间隙谐振器的归一化电子负载电纳与渡越角的关系
Figure 7. Bb5/G0 versus θ0 of five-gap cavity.
图 8 五间隙谐振器的归一化电子负载电纳与βeL的关系
Figure 8. Bb5/G0 versus βeL of five-gap cavity.
图 9 不同间隙数谐振器的归一化电子负载电纳与渡越角的关系
Figure 9. BbN/G0 versus θ0 of multiple-gap cavity.
图 10 不同间隙数谐振器的归一化电子负载电纳与βeL的关系
Figure 10. BbN/G0 versus βeL of multiple-gap cavity.
图 11 五间隙数谐振器的电子负载电导与工作电压的关系
Figure 11. Gb5 versus U0 of five-gap cavity.
图 12 五间隙数谐振器的电子负载电导与工作电压的关系
Figure 12. Gb5 versus U0 of five-gap cavity.
图 13 扩展互作用速调管高频结构模型
Figure 13. Model of the extended interaction klystron.
图 14 输入腔各模式Ez沿轴向的分布
Figure 14. Ez versus axial distance of each mode in input cavity.
图 15 中间腔各模式Ez沿轴向的分布
Figure 15. Ez versus axial distance of each mode in middle cavity.
图 16 输出腔各模式Ez沿轴向的分布
Figure 16. Ez versus axial distance of each mode in output cavity.
图 17 输入腔各模式Qt与电压U0的关系
Figure 17. Qt versus U0 of each mode in input cavity.
图 18 中间腔各模式Qt与电压U0的关系
Figure 18. Qt versus U0 of each mode in middle cavity.
图 19 输出腔各模式Qt与电压U0的关系
Figure 19. Qt versus U0 of each mode in output cavity.
图 20 瞬时输入功率波形
Figure 20. Waveform of input microwave.
图 21 调制电流基频分量沿轴向的分布
Figure 21. Fundamental modulated current amplitude versus axial distance.
图 22 瞬时输出功率波形
Figure 22. Instantaneous waveform of output microwave.
图 23 输出功率频谱
Figure 23. Spectrum of output microwave.
图 24 输出功率和电子效率与输入微波频率的关系
Figure 24. Output power and efficiency versus input microwave frequency.
图 27 输出功率和电子效率与电流的关系
Figure 27. Output power and efficiency versus current.
图 25 输出功率和电子效率与输入微波功率的关系
Figure 25. Output power and efficiency versus input microwave power.
图 26 输出功率和电子效率与电子注电压的关系
Figure 26. Output power and efficiency versus voltage.
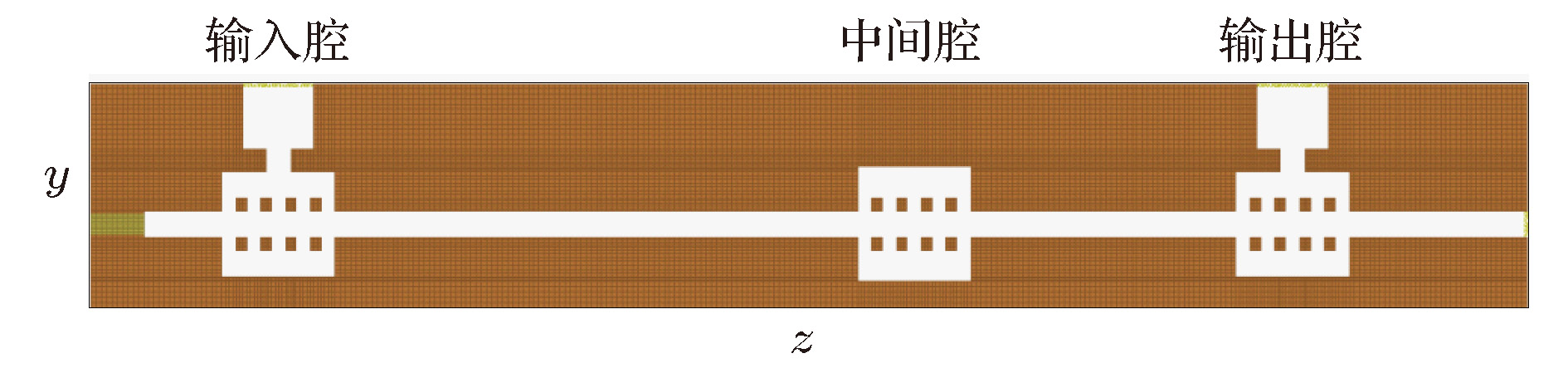
表 1 G波段扩展互作用速调管高频结构参数
Table 1. Structural parameters of G-band extended interaction klystron amplifier.
谐振腔 纵向工作模式 谐振频率/GHz 固有品质因数Q0 外观品质因数Qext 起始位置/mm 输入腔 ${\text{π}}$模 218 413 380 0 中间腔 ${\text{π}}$模 218.05 413 ∞ 4.87 输出腔 ${\text{π}}$模 218 413 1940 7.77 
DownLoad: CSV
-
[1] 刘振帮, 赵欲聪, 黄华, 金晓, 雷禄容 2015 64 108404
Google Scholar
Liu Z B, Zhao Y C, Huang H, Jin X, Lei L R 2015 Acta Phys. Sin. 64 108404
Google Scholar
[2] Gutiérrez J, Pascual J P, Tazón A 2018 Int. J. RF Microwave Comput. Aided Eng. 28 21284
Google Scholar
[3] Rhoads C, Goshi D S 2018 IEEE Radar Conference Oklahoma, USA, April 23−27, 2018 p0344
[4] 刘国, 王建勋, 罗勇 2013 62 078404
Google Scholar
Liu G, Wang J X, Luo Y 2013 Acta Phys. Sin. 62 078404
Google Scholar
[5] 陈姝媛, 阮存军, 王勇, 张长青, 钟勇, 赵鼎 2015 红外与毫米波学报 34 230
Google Scholar
Chen S Y, Ruan C J, Wang Y, Zhang C Q, Zhong Y, Zhao D 2015 J. Infrared Millmeter Waves 34 230
Google Scholar
[6] Feng J J, Cai J, Hu Y F, Wu X P, Du Y H, Liu J K, Pan P, Li H Y 2014 IEEE Trans. Electron Dev. 61 1721
Google Scholar
[7] Gerum W, Lippert G, Malzahn P, Schneider K 2001 IEEE Trans. Electron Dev. 48 72
Google Scholar
[8] Richard K, Andrew Z, Clark M, Mike M, Mark K, Richard T, Ai T, John R, Carter A 2013 IEEE International Vacuum Electronics Conference Paris, France, May 21−23, 2013 p1
[9] 吴洋, 许州, 周霖, 李文君, 唐传祥 2012 61 224101
Google Scholar
Wu Y, Xu Z, Zhou L, Li W J, Tang C X 2012 Acta Phys. Sin. 61 224101
Google Scholar
[10] Maslennikov S P, Paramonov Y N, Serebryakova A S 2018 IEEE International Vacuum Electronics Conference Monterey, USA, April 24−26, 2018 p215
[11] She J C, Huang Z Z, Huang Y F, Huang Z J, Chen J, Deng S Z, Xu N S 2017 International Vacuum Nanoelectronics Conference, Regensburg Germany, July 10−14, 2017 p4
[12] Li R J, Ruan C J, Zhang H F 2018 Phys. Plasmas 25 033107
Google Scholar
[13] Toreev A I, Fedorov V K, Patrusheva E V 2009 J. Commun. Technol. Electron. 54 952
Google Scholar
[14] Dave B, Henry D, Richard D, Peter H, Mark H, Andrew K, Ross M, Albert R, Ed S, Brian S 2014 IEEE Trans. Electron Devices 61 1830
Google Scholar
[15] Chang Z W, Meng L, Yin Y, Wang B, Li H L, Rauf A, Ullah S, Bi L J, Peng R B 2018 IEEE Trans. Electron Dev. 65 1179
Google Scholar
[16] Qu Z W, Zhang Z Q, Ding Y G, Wang S Z, Li Q S 2018 IEEE International Vacuum Electronics Conference Monterey, USA, April 24−26, 2018 p189
[17] Albert R, Dave B, Brian S 2018 IEEE Trans. Electron Dev. 52 895
[18] Brian S, Albert R, Peter H, Mark H, Richard D, Dave B 2011 Proceedings of the 41st European Microwave Conference Manchester, UK, Oct 10−13, 2011 p984
[19] Hu L L, Zeng Z J, Chen H B, Ma G W, Meng F B 2018 J. Eng. 2018 689
[20] Li R J, Ruan C J 2017 IEEE International Vacuum Electronics Conference London, UK, April 24−26, 2017 p1
[21] Li S F, Duan Z Y, Wang F, Wang Z L, Xu J, Gong Y B 2014 Int. Conf. Infrared, Millim., Terahertz Waves, Tucson, USA, September 14−19, 2014 p2
[22] Zhong Y, Liu W X, Wang Y, Ruan C J, Wang S Z 2012 Int. Conf. Infrared, Millim., Terahertz Waves Wollongong, Australia, September 23−28, 2012 p1
[23] 盛兴, 韦莹, 孙福江, 王瑞海, 冯海平, 胡晓斌 2012 真空电子技术 2 19
Google Scholar
Sheng X, Wei Y, Sun F J, Wang R H, Feng H P, Hu X B 2012 Vacuum Electronics 2 19
Google Scholar
[24] 曾造金 2014 硕士学位论文 (成都: 电子科技大学)
Zeng Z J 2014 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[25] 谢家麟, 赵永翔 1966 速调管群聚理论 (北京: 科学出版社) 第33−177页
Xie J L, Zhao Y X 1966 Bunching Theory of Klystron (Beijing: Science Press) pp33−177 (in Chinese)
[26] 丁耀根 2008 大功率速调管的理论与计算模拟 (北京: 国防工业出版社) 第44−75页
Ding Y G 2008 Theory and Computer Simulation of High Power Klystron (Beijing: National Defense Industry Press) pp44−75 (in Chinese)
[27] Zhao Y C, Li S F, Huang H, Liu Z B, Wang Z L, Dan Z Y, Li X Y, Wei Y Y, Gong Y B 2015 IEEE Trans. Plasma Sci. 43 1862
Google Scholar
[28] 范植开, 刘庆想, 刘锡三, 周传民, 胡海膺 1999 强激光与粒子束 11 633
Fan Z K, Liu Q X, Liu X S, Zhou C M, Hu H Y 1999 High Power Laser and Particle Beams 11 633
[29] Lemke R W, Clark M C, Marder B M 1994 J. Appl. Phys. 75 10
[30] 范植开, 刘庆想, 刘锡三, 何琥, 周传民 1999 强激光与粒子束 11 482
Fan Z K, Liu Q X, Liu X S, He H, Zhou C M 1999 High Power Laser and Particle Beams 11 482
[31] Marcum J 1946 J. Appl. Phys. 17 4
Google Scholar
[32] Marder B M, Clark M C, Bacon L D, Hoffman J M, Lemke R W, Coleman P D 1992 IEEE Trans. Plasma Sci. 20 312
Google Scholar
[33] Carlsten B E, Haynes W B 1996 IEEE Trans. Plasma Sci. 24 1249
Google Scholar
[34] 范植开 1999 博士学位论文(北京: 中国工程物理研究院)
Fan Z K 1999 Ph. D. Dissertation (Beijing: China Academy of Engineering Physics) (in Chinese)
[35] 哈依柯夫 著 (黄高年 译) 1980 速调管放大器 (北京: 国防工业出版社) 第92, 93页
Eckertova L (translated by Hang G N) 1980 Клиотронные усилители (Beijing: National Defense Industry Press) pp92, 93 (in Chinese)
[36] Zhang Z H, Shu T, Zhang J, Qi Z M, Zhu J 2012 IEEE Trans. Plasma Sci. 40 3121
Google Scholar
[37] 徐翱, 周泉丰, 阎磊, 陈洪斌 2013 强激光与粒子束 25 2954
Xu A, Zhou Q F, Yan L, Chen H B 2013 High Power Laser and Particle Beams 25 2954
[38] Hsu H L 2006 Ph. D. Dissertation (Davis: University of California)
DownLoad:
Catalog
Metrics
- Abstract views: 7866
- PDF Downloads: 51
- Cited By: 0
