W波段分布作用速调管的设计和实验研究

曾造金; 胡林林; 马乔生; 蒋艺; 陈洪斌

doi:10.7498/aps.68.20182194

摘要

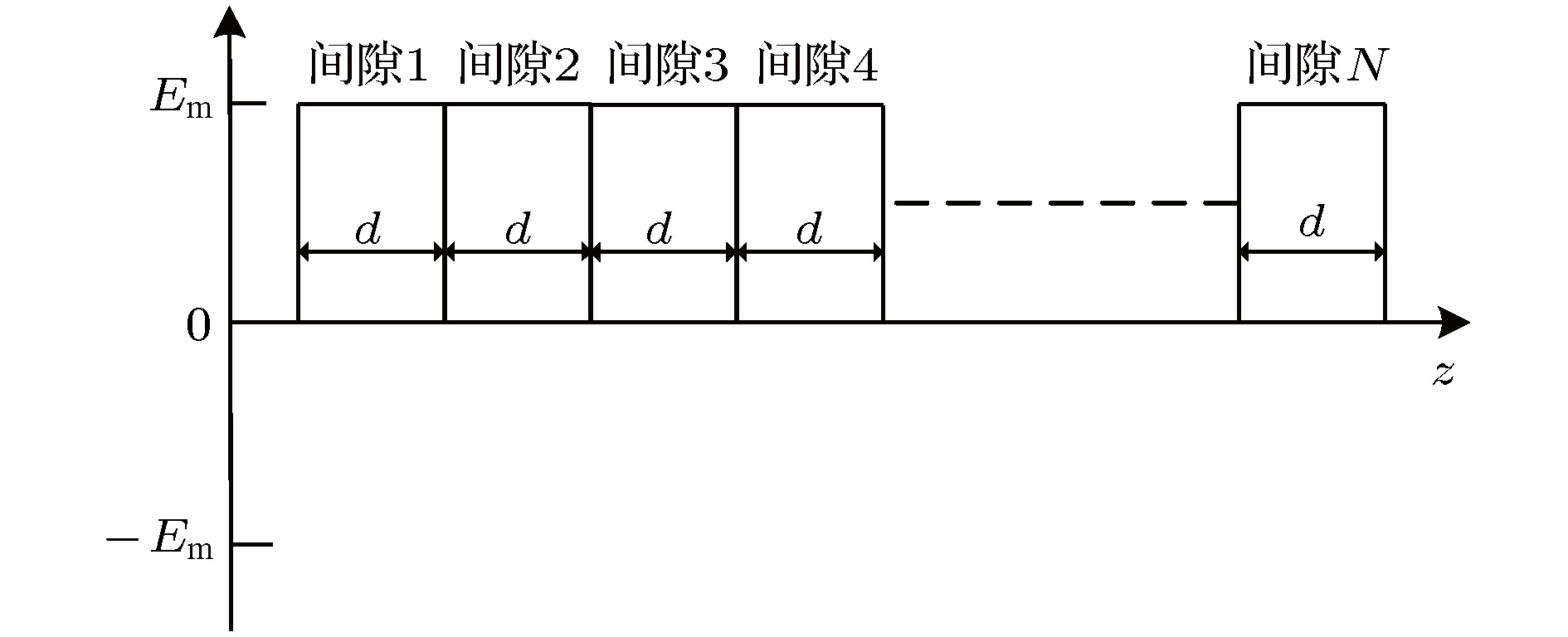
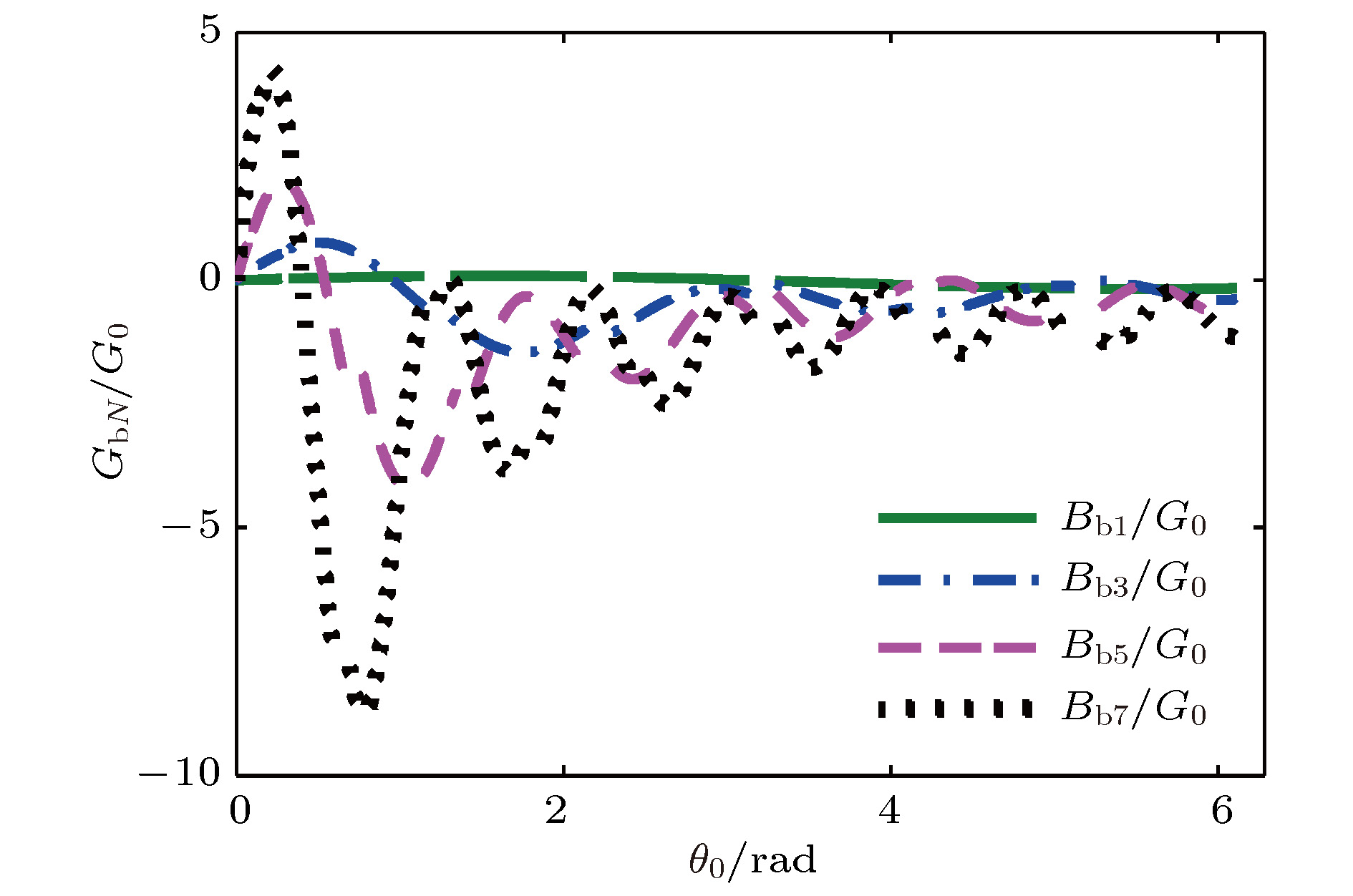
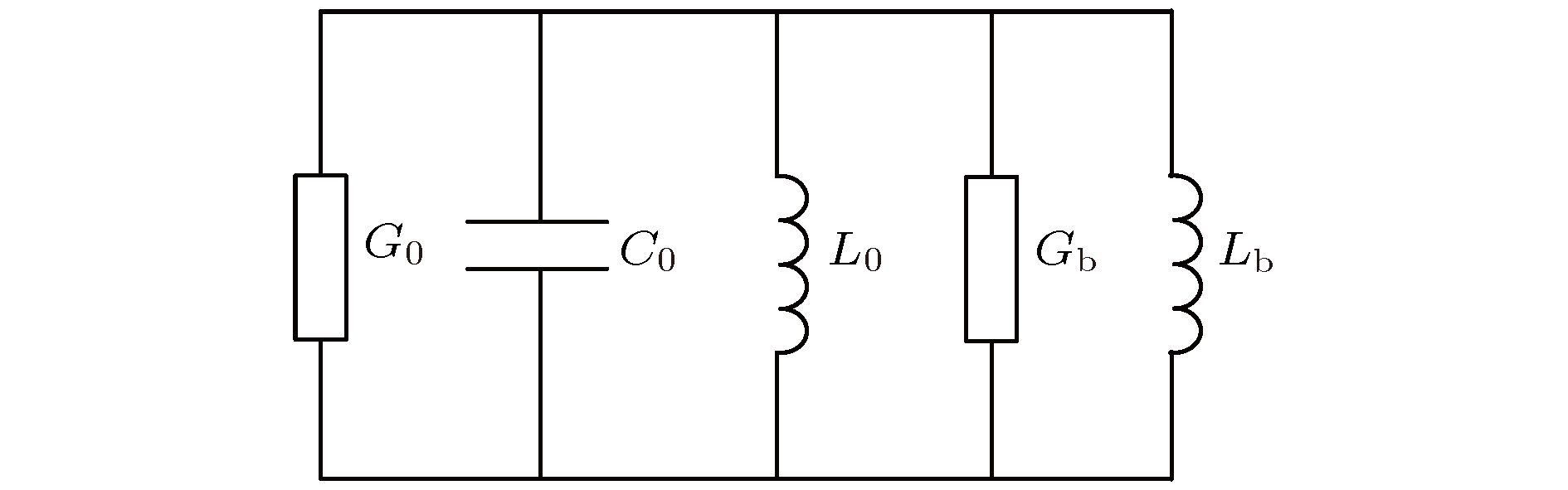
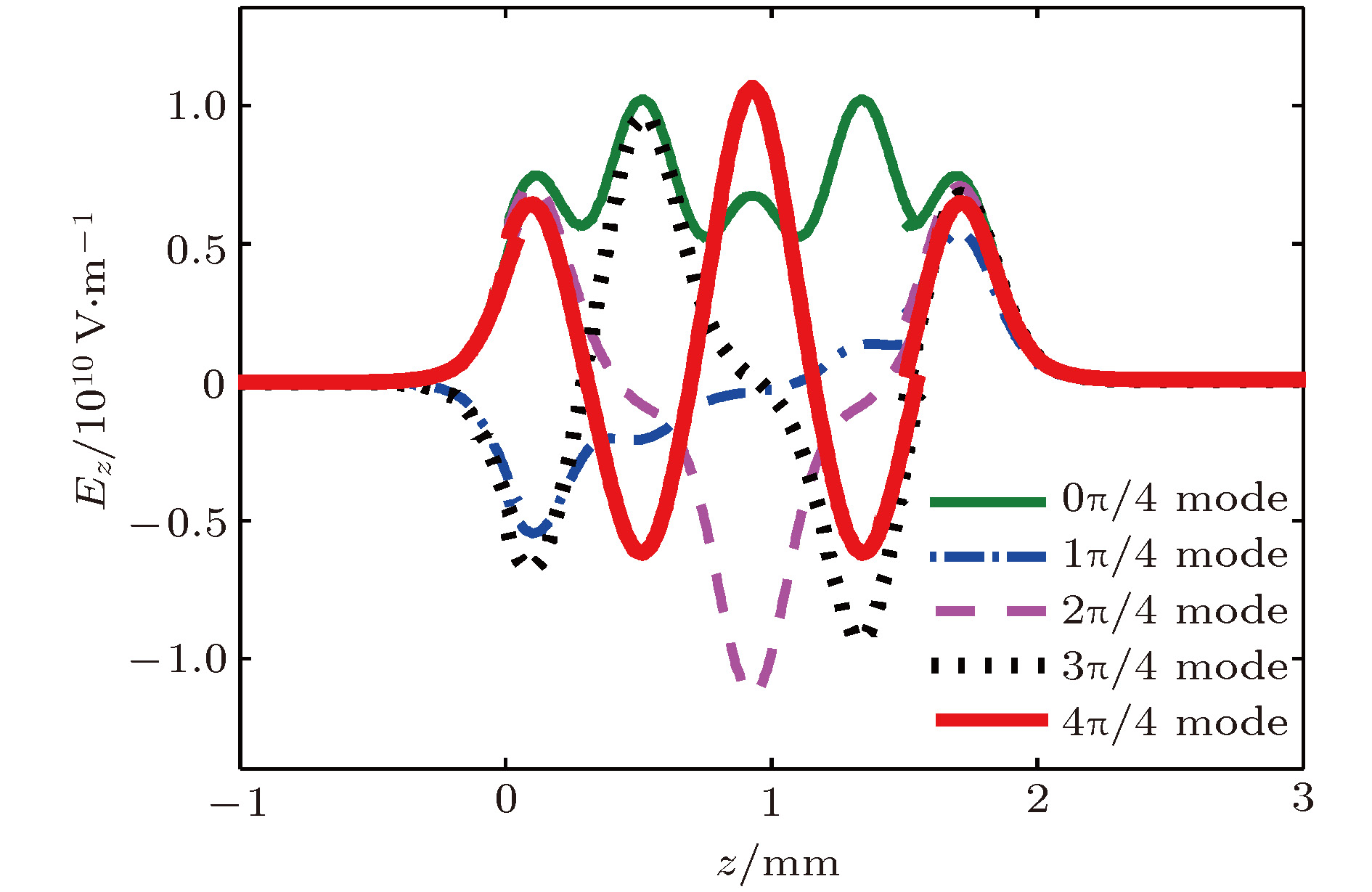
基于运动学理论、感应电流定理和电荷守恒定律, 分析了分布作用谐振腔的渡越时间效应, 推导了各个谐振腔工作于${\text{π}}$模的电子注与微波之间的能量转换系数、电子负载电导和电子负载电纳, 计算结果显示采用分布作用谐振腔有利于提高速调管的工作效率. 利用三维电磁仿真软件, 设计了一款工作于W波段的分布作用速调管. 完成了速调管的加工和封接, 搭建了测试平台, 开展了相关实验研究. 实验结果显示, 当电子注电压20.8 kV, 电流0.3 A, 输入功率30 mW时, 在中心频率95.37 GHz处, 得到了175 W峰值脉冲输出功率, 电子效率2.8%, 增益34.6 dB, 3 dB带宽大于90 MHz.

关键词:

Abstract

Beam loading is an important parameter in extended interaction klystron, which can be used to analyze the influence of beam on resonant frequency and ohm loss Q, and study the match condition between input cavity and external power source, etc. Based on the kinematical theory, law of induce current, principle of charge conservation under the small signal condition, and one-dimensional (1D) mode, the transit time effect of electron in ${\text{π}}$ mode standing wave electric treld in a multiple-gap resonator is analyzed, and the expressions of electron load conductance and electron load susceptance in the multiple-gap resonator are presented. The results show that the electron load conductance of extended interaction cavity can change in a bigger extension than that of traditional single gap cavity, which means that the loaded Q of extended interaction cavity can be adjusted in a bigger extension to realize a desired Q. And the results also show that the electron load susceptance of extended interaction cavity can change in a bigger extension than that of traditional single gap cavity, which means that the loaded frequency of extended interaction cavity can also be easily adjusted to a desired value. The influence of gap number on the power exchange between beam and microwave is also investigated, which shows that the maximum power exchange between beam and microwave electric field increases with the number of resonator gaps increasing, and so does the efficiency of klystron. A W band extended interaction klystron amplifoer is designed by the above theory analysis and three-dimensional (3D) PIC code. The simulation results show that when beam voltage is 20.8 kV, current is 0.28 A, input power is 30 mW at a frequency of 94.77 GHz, the extended interaction klystron can produce 443 W output power. The responding electron efficiency is 7.6%, the gain is 41.7 dB, and the 3 dB bandwidth exceeds 150 MHz. The extended interaction klystron is machined and tested, and the experimental results show that the maximum output power of 175 W is obtained with a beam of 300 mA, a voltage of 20.8 kV, and an input microwave power of 30 mW at a frequency of 95.37 GHz in a magnetic field of 0.62 T. The responding electron efficiency is 2.8%, the gain is 34.6 dB, the 3-dB bandwidth exceeds 90 MHz. This study is meaningful for designing and developing greater power extended interaction klystrons.

Keywords:

作者及机构信息

中国工程物理研究院应用电子学研究所, 绵阳 621900

通信作者: 陈洪斌, 17721915695@163.com

Authors and contacts

Institute of Applied Electronics, Chinese Academy of Engineering Physics, Mianyang 621900, China

Corresponding author: Chen Hong-Bin, 17721915695@163.com

文章全文 : translate this paragraph

参考文献

[1]	Toreev A I, Fedorov V K, Patrusheva E V 2009 J. Commun. Technol. Electron. 54 952 Google Scholar
[2]	Brian S, Albert R, Peter H, Mark H, Richard D, Dave B IEEE Pulse Power Plasma Science Conference Albuquerque, USA, June 17−22, 2007 p1049
[3]	Brian S, Albert R, Peter H, Mark H, Richard D, Dave B IEEE Radar Conference Pasadena, USA, May 4−8, 2009 p1
[4]	Toreev A I, Fedorov V K 2011 Appl. Phys. 52 109
[5]	吴洋, 许州, 周霖, 李文君, 唐传祥 2012 61 224101 Google Scholar Wu Y, Xu Z, Zhou L, Li W J, Tang C X 2012 Acta Phys. Sin. 61 224101 Google Scholar
[6]	刘振帮, 赵欲聪, 黄华, 金晓, 雷禄容 2015 64 108404 Liu Z B, Zhao Y C, Huang H, Jin X, Lei L R 2015 Acta Phys. Sin. 64 108404
[7]	丁耀根 2010 大功率速调管的设计制造和应用 (北京: 国防工业出版社) 第8—17页 Ding Y G 2010 Design, Manufacture and Application of High Power Klystron (Beijing: National Defense Industry Press) pp8−17 (in Chinese)
[8]	Albert R, Dave B, Brian S 2005 IEEE Trans. Electron Devices 52 895 Google Scholar
[9]	Brian S, Albert R, Peter H, Mark H, Richard D, Dave B 2011 41st European Microwave Conference Manchester, UK, Oct 10−13, 2011 p984
[10]	Peter H, Dave B, Brian S IEEE International Vacuum Electronics Conference Kitakytushu, Japan, May 15−17, 2007 p149
[11]	韦莹, 殷亮, 杨继涛, 周军, 李东凤, 欧阳佳佳, 窦钺, 钟勇 2018 中国电子学会真空电子学分会第二十一届学术年会中国平凉 2018年8月23—26日第218页 Wei Y, Yin L, Yang J T, Zhou J, Li D F, Ouyang J J, Dou Y, Zhong Y 2018 The Chinese Institute of Electronics Conference on Vacuum Electronics Pingliang, China, Aug. 23−26, 2018 p218 (in Chinese)
[12]	范植开, 刘庆想, 刘锡三, 周传民, 胡海膺 1999 强激光与粒子束 11 633 Fan Z K, Liu Q X, Liu X S, Zhou C M, Hu H Y 1999 High Power Laser and Particle Beams 11 633
[13]	Zhao Y C, Li S F, Huang H, Liu Z B, Wang Z L, Dan Z Y, Li X Y, Wei Y Y, Gong Y B 2015 IEEE Trans. Plasma Sci. 43 1862 Google Scholar
[14]	Marcum J 1946 J. Appl. Phys. 17 4 Google Scholar
[15]	Marder B M, Clark M C, Bacon L D, Hoffman J M, Lemke R W, Coleman P D 1992 IEEE Trans. Plasma Sci. 20 312 Google Scholar
[16]	Yuan Y S, Li K W, Wang N, Yoshiro I, Wang S 2015 Chin. Phys. C 39 047003 Google Scholar
[17]	曾造金 2014 硕士学位论文(成都: 电子科技大学) Zeng Z J 2014 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[18]	谢家麟, 赵永翔1966 速调管群聚理论(北京: 科学出版社) 第33—37页 Xie J L, Zhao Y X 1966 Bunching Theory of Klystron (Beijing: Science Press) p33−37 (in Chinese)
[19]	Li R J, Ruan C J, Zhang H F, Haq T U, He Y B, Shan S Y 2018 IEEE Trans. Electron Devices 65 3500 Google Scholar
[20]	丁耀根 2008 大功率速调管的理论与计算模拟(北京: 国防工业出版社) 第75 页 Ding Y G 2008 Theory and Computer Simulation of High Power Klystron (Beijing: National Defense Industry Press) p75 (in Chinese)
[21]	张泽海, 舒挺, 张军, 戚祖敏 2013 62 040701 Google Scholar Zhang Z H, Shu T, Zhang J, Qi Z M 2013 Acta Phys. Sin. 62 040701 Google Scholar
[22]	陈永东, 金晓, 李正红, 黄华, 吴洋 2012 61 228501 Google Scholar Chen Y D, Jin X, Li Z H, Huang H, Wu Y 2012 Acta Phys. Sin. 61 228501 Google Scholar
[23]	Bi L J, Yin Y, Xu C P, Zhang Z, Chang Z W, Zeng F B, Peng R B, Zhou W, Rauf A, Ullah S, Wang B, Li H L, Meng L 2017 IEEE Trans. Electron Devices 64 4686 Google Scholar

施引文献

图 1 谐振腔等效电路

Fig. 1. Equivalent circuit mode of cavity.

下载: 全尺寸图片幻灯片

图 2 引入电子注后谐振腔等效电路

Fig. 2. Equivalent circuit mode of cavity with beam.

下载: 全尺寸图片幻灯片

图 3 多间隙谐振腔${\text{π}}$模场示意图

Fig. 3. E-field of ${\text{π}}$ mode in multiple-gap cavity.

下载: 全尺寸图片幻灯片

图 4 多间隙谐振腔${\text{π}}$模场简化图

Fig. 4. Simplified E-field of ${\text{π}}$ mode in multiple-gap cavity.

下载: 全尺寸图片幻灯片

图 5 归一化电子负载电导与渡越角的关系

Fig. 5. G_bN/G₀ versus θ₀ of multiple-gap cavity.

下载: 全尺寸图片幻灯片

图 6 归一化电子负载电纳与渡越角的关系

Fig. 6. B_bN/G₀ versus θ₀ of multiple-gap cavity.

下载: 全尺寸图片幻灯片

图 7 B_bN为正值谐振腔等效电路

Fig. 7. Equivalent circuit mode of cavity when B_bN > 0.

下载: 全尺寸图片幻灯片

图 8 B_bN为负值时谐振腔等效电路

Fig. 8. Equivalent circuit mode of cavity when B_bN < 0.

下载: 全尺寸图片幻灯片

图 9 分布作用速调管高频结构模型

Fig. 9. Model of the extended interaction cavity.

下载: 全尺寸图片幻灯片

图 10 输入腔各模式E_z沿轴向的分布

Fig. 10. E_z versus axial distance of each mode in input cavity

下载: 全尺寸图片幻灯片

图 11 中间腔各模式E_z沿轴向的分布

Fig. 11. E_z versus axial distance of each mode in middle cavity.

下载: 全尺寸图片幻灯片

图 12 输入腔各模式Q_total与电压U的关系

Fig. 12. Q_total versus U of each mode in input cavity.

下载: 全尺寸图片幻灯片

图 13 中间腔各模式Q_total与电压U的关系

Fig. 13. Q_total versus U of each mode in middle cavity.

下载: 全尺寸图片幻灯片

图 14 瞬时输入功率波形

Fig. 14. Waveform of input microwave.

下载: 全尺寸图片幻灯片

图 15 调制电流基频分量沿轴向的分布

Fig. 15. fundamental modulated current amplitude versus axial distance.

下载: 全尺寸图片幻灯片

图 16 瞬时输出功率波形

Fig. 16. Waveform of output microwave.

下载: 全尺寸图片幻灯片

图 17 输出功率与输入信号频率的关系

Fig. 17. Output power versus input frequency.

下载: 全尺寸图片幻灯片

图 18 分布作用速调管实物

Fig. 18. Picture of extended interaction klystron.

下载: 全尺寸图片幻灯片

图 19 分布作用速调管测试系统

Fig. 19. Test system of extended interaction klystron.

下载: 全尺寸图片幻灯片

图 20 高频样管测试结果

Fig. 20. Test result of extended interaction klystron.

下载: 全尺寸图片幻灯片

图 21 高频样管输出功率与输入信号频率的关系

Fig. 21. Measured output power vs input frequency.

下载: 全尺寸图片幻灯片

map

[1]	Toreev A I, Fedorov V K, Patrusheva E V 2009 J. Commun. Technol. Electron. 54 952 Google Scholar
[2]	Brian S, Albert R, Peter H, Mark H, Richard D, Dave B IEEE Pulse Power Plasma Science Conference Albuquerque, USA, June 17−22, 2007 p1049
[3]	Brian S, Albert R, Peter H, Mark H, Richard D, Dave B IEEE Radar Conference Pasadena, USA, May 4−8, 2009 p1
[4]	Toreev A I, Fedorov V K 2011 Appl. Phys. 52 109
[5]	吴洋, 许州, 周霖, 李文君, 唐传祥 2012 61 224101 Google Scholar Wu Y, Xu Z, Zhou L, Li W J, Tang C X 2012 Acta Phys. Sin. 61 224101 Google Scholar
[6]	刘振帮, 赵欲聪, 黄华, 金晓, 雷禄容 2015 64 108404 Liu Z B, Zhao Y C, Huang H, Jin X, Lei L R 2015 Acta Phys. Sin. 64 108404
[7]	丁耀根 2010 大功率速调管的设计制造和应用 (北京: 国防工业出版社) 第8—17页 Ding Y G 2010 Design, Manufacture and Application of High Power Klystron (Beijing: National Defense Industry Press) pp8−17 (in Chinese)
[8]	Albert R, Dave B, Brian S 2005 IEEE Trans. Electron Devices 52 895 Google Scholar
[9]	Brian S, Albert R, Peter H, Mark H, Richard D, Dave B 2011 41st European Microwave Conference Manchester, UK, Oct 10−13, 2011 p984
[10]	Peter H, Dave B, Brian S IEEE International Vacuum Electronics Conference Kitakytushu, Japan, May 15−17, 2007 p149
[11]	韦莹, 殷亮, 杨继涛, 周军, 李东凤, 欧阳佳佳, 窦钺, 钟勇 2018 中国电子学会真空电子学分会第二十一届学术年会中国平凉 2018年8月23—26日第218页 Wei Y, Yin L, Yang J T, Zhou J, Li D F, Ouyang J J, Dou Y, Zhong Y 2018 The Chinese Institute of Electronics Conference on Vacuum Electronics Pingliang, China, Aug. 23−26, 2018 p218 (in Chinese)
[12]	范植开, 刘庆想, 刘锡三, 周传民, 胡海膺 1999 强激光与粒子束 11 633 Fan Z K, Liu Q X, Liu X S, Zhou C M, Hu H Y 1999 High Power Laser and Particle Beams 11 633
[13]	Zhao Y C, Li S F, Huang H, Liu Z B, Wang Z L, Dan Z Y, Li X Y, Wei Y Y, Gong Y B 2015 IEEE Trans. Plasma Sci. 43 1862 Google Scholar
[14]	Marcum J 1946 J. Appl. Phys. 17 4 Google Scholar
[15]	Marder B M, Clark M C, Bacon L D, Hoffman J M, Lemke R W, Coleman P D 1992 IEEE Trans. Plasma Sci. 20 312 Google Scholar
[16]	Yuan Y S, Li K W, Wang N, Yoshiro I, Wang S 2015 Chin. Phys. C 39 047003 Google Scholar
[17]	曾造金 2014 硕士学位论文(成都: 电子科技大学) Zeng Z J 2014 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[18]	谢家麟, 赵永翔1966 速调管群聚理论(北京: 科学出版社) 第33—37页 Xie J L, Zhao Y X 1966 Bunching Theory of Klystron (Beijing: Science Press) p33−37 (in Chinese)
[19]	Li R J, Ruan C J, Zhang H F, Haq T U, He Y B, Shan S Y 2018 IEEE Trans. Electron Devices 65 3500 Google Scholar
[20]	丁耀根 2008 大功率速调管的理论与计算模拟(北京: 国防工业出版社) 第75 页 Ding Y G 2008 Theory and Computer Simulation of High Power Klystron (Beijing: National Defense Industry Press) p75 (in Chinese)
[21]	张泽海, 舒挺, 张军, 戚祖敏 2013 62 040701 Google Scholar Zhang Z H, Shu T, Zhang J, Qi Z M 2013 Acta Phys. Sin. 62 040701 Google Scholar
[22]	陈永东, 金晓, 李正红, 黄华, 吴洋 2012 61 228501 Google Scholar Chen Y D, Jin X, Li Z H, Huang H, Wu Y 2012 Acta Phys. Sin. 61 228501 Google Scholar
[23]	Bi L J, Yin Y, Xu C P, Zhang Z, Chang Z W, Zeng F B, Peng R B, Zhou W, Rauf A, Ullah S, Wang B, Li H L, Meng L 2017 IEEE Trans. Electron Devices 64 4686 Google Scholar

[1]	曾造金, 马乔生, 胡林林, 蒋艺, 胡鹏, 雷文强, 马国武, 陈洪斌. W波段带状注扩展互作用速调管放大器的理论研究与数值模拟. , 2019, 68(24): 248401. doi: 10.7498/aps.68.20190907
[2]	曾造金, 马乔生, 胡林林, 蒋艺, 胡鹏, 陈洪斌. G波段扩展互作用速调管的理论分析与设计. , 2019, 68(15): 154102. doi: 10.7498/aps.68.20190264
[3]	刘振帮, 赵欲聪, 黄华, 金晓, 雷禄容. Ka波段带状注相对论扩展互作用速调管放大器的分析与设计. , 2015, 64(10): 108404. doi: 10.7498/aps.64.108404
[4]	薛智浩, 刘濮鲲, 杜朝海. W波段螺旋波纹波导回旋行波管注波互作用的非线性分析. , 2014, 63(8): 080201. doi: 10.7498/aps.63.080201
[5]	陈永东, 吴洋, 谢鸿全, 李正红, 周自刚. 相对论速调管中间腔与调制电子束间的非线性互作用. , 2013, 62(10): 104104. doi: 10.7498/aps.62.104104
[6]	刘国, 王建勋, 罗勇. W波段带状注速调管准光输出结构改进设计. , 2013, 62(7): 078404. doi: 10.7498/aps.62.078404
[7]	谢文球, 王自成, 罗积润, 刘青伦, 董芳. 基于开槽单矩形栅和圆形电子注的W波段返波振荡器. , 2013, 62(15): 158503. doi: 10.7498/aps.62.158503
[8]	薛智浩, 刘濮鲲, 杜朝海, 李铮迪. W波段螺旋波纹波导回旋行波管注波互作用的非线性分析. , 2012, 61(17): 170201. doi: 10.7498/aps.61.170201
[9]	刘维浩, 张雅鑫, 胡旻, 周俊, 刘盛纲. 基于场致发射阴极阵列的太赫兹源的物理机理研究. , 2012, 61(12): 127901. doi: 10.7498/aps.61.127901
[10]	吴洋, 许州, 周霖, 李文君, 唐传祥. W波段扩展互作用速调管放大器的模拟与设计. , 2012, 61(22): 224101. doi: 10.7498/aps.61.224101
[11]	王斌, 杜朝海, 刘濮鲲, 耿志辉, 徐寿喜. W波段边廊模回旋管准光模式变换器的研究与设计. , 2010, 59(4): 2512-2518. doi: 10.7498/aps.59.2512
[12]	杜坚, 张鹏, 刘继红, 李金亮, 李玉现. 含δ势垒的铁磁/半导体/铁磁异质结中的自旋输运和渡越时间. , 2008, 57(11): 7221-7227. doi: 10.7498/aps.57.7221
[13]	王光昶, 郑志坚, 谷渝秋, 陈涛, 张婷. 利用渡越辐射研究超热电子在固体靶中的输运过程. , 2007, 56(2): 982-987. doi: 10.7498/aps.56.982
[14]	谭世杰, 郑坚. 不同加热机制产生的超热电子的相干渡越辐射谐波研究. , 2007, 56(12): 7132-7137. doi: 10.7498/aps.56.7132
[15]	来国军, 刘濮鲲. W波段二次谐波回旋行波管放大器的模拟与设计. , 2007, 56(8): 4515-4522. doi: 10.7498/aps.56.4515
[16]	远晓辉, 李玉同, 徐妙华, 于全芝, 王首钧, 张杰, 赵卫, 王光昶, 温贤伦, 焦春晔, 何颖伶, 张双根, 王向贤, 黄文忠, 谷渝秋. 超热电子产生的靶后相干渡越辐射光谱实验研究. , 2006, 55(10): 5362-5367. doi: 10.7498/aps.55.5362
[17]	来国军, 刘濮鲲. W波段回旋行波管放大器的模拟与设计. , 2006, 55(1): 321-325. doi: 10.7498/aps.55.321
[18]	蒋华北. 受激渡越辐射光学速调管. , 1990, 39(1): 61-66. doi: 10.7498/aps.39.61-2
[19]	刘福绥, 范希庆, 刘砚章, 王淮生, 阮英超. 电子多声子作用对散射时间的效应. , 1989, 38(1): 154-158. doi: 10.7498/aps.38.154
[20]	刘盛纲, 孙雁. 渡越辐射自由电子激光中自发辐射与受激辐射的关系. , 1988, 37(9): 1505-1509. doi: 10.7498/aps.37.1505

计量

文章访问数: 8247
PDF下载量: 76
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

W波段分布作用速调管的设计和实验研究