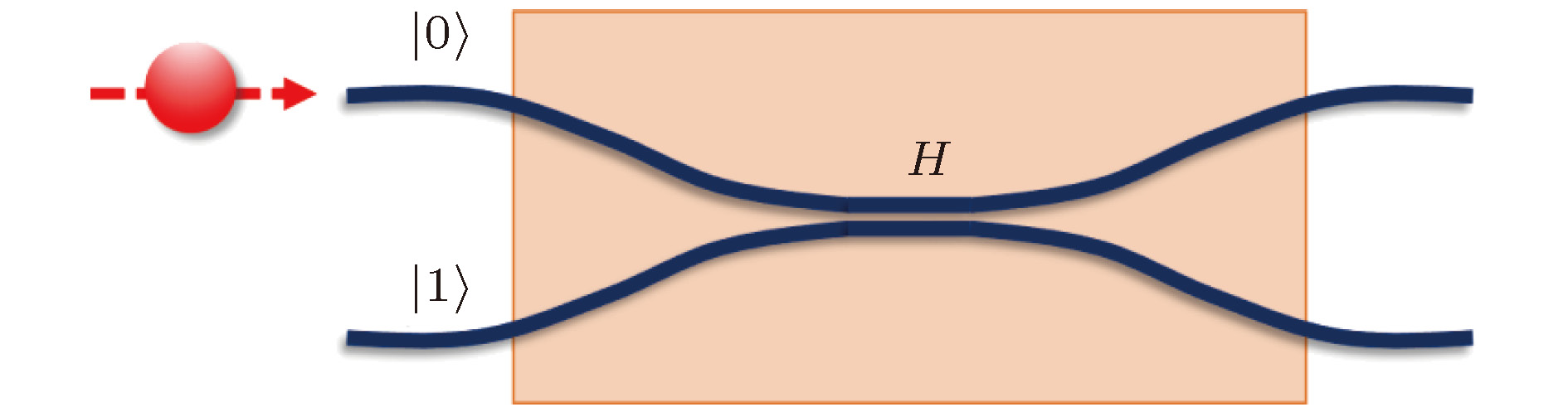
-
Unlike classical digital computers in which a bit can represent either 1 or 0 at any time, quantum computers use a two-level system, i.e., a qubit, to implement logical operations based on quantum mechanical laws, which can represent both values at once. Owing to the superposition property of qubits, quantum computers have natural parallel processing advantages and thus have potential to exceed the computational efficiency of classical computers for particular tasks. Quantum logic gates are the generalization of classical logic gates in computational networks. It has been proved that two-qubit quantum gates together with one-qubit quantum gates are adequate for constructing networks with any possible quantum computational property. Directional couplers are the most critical elementsfor constructing the quantum gates. In recent years, photonic quantum technologies have emerged as a promising experimental platform for quantum computing. Single photons have robust noise resistance, long coherence time, high transmission speed and great compatibility with other systems. They can be easily manipulated and encoded in any of several degrees of freedom, for example, polarization, path, spatial mode or time bin. Optical waveguide technology enables the realizing of complex optical schemes comprised of many elements with desired scalability, stability and miniaturization. Femtosecond laser direct writing of waveguide has been adopted as a powerful tool for integrated quantum photonics with characteristics of rapidness, cost-effectiveness, mask-less and single-step process. In particular, it has the ability to build arbitrary three-dimensional circuits directly inside bulk materials, which is impossible to achieve with conventional lithography. In this article we review the femtosecond laser writing and quantum characterization of directional coupler and important one-qubit and two-qubit optical quantum logic gates, such as Hadamard gate, Pauli-X gate, controlled-NOT gate, and controlled-Phase gate. The qubits in these gates are usually encoded through optical paths or polarizations of photons. The key to the realization of polarization-encoded one-qubit gates is to achieve flexible wave-plate operations, which is described in detail. Controlled-NOT gate and controlled-phase gate are the most crucial two-qubit gates in the linear optics computation and sometimes they can be converted into each other by adding some one-qubit gates or special superposition states. Many different kinds of waveguide circuits have been used to implement these two-qubit gates. The outlook and challenges for the femtosecond laser writing of three-qubit gates, such as Toffoli gate and Fredkin gate, are briefly introduced.
-
Keywords:
- quantum logic gate /
- femtosecond laser direct writing /
- optical waveguide /
- directional coupler
[1] Bennett C H 1995 Phys. Today 48 24
[2] Galindo A, Martin-Delgado M A 2002 Rev. Mod. Phys. 74 347
Google Scholar
[3] 范桁 2018 67 120301
Google Scholar
Fan H 2018 Acta Phys. Sin. 67 120301
Google Scholar
[4] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[5] Grover L K 1996 Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing Philadelphia, PA, USA, May 22 – 24, 1996 p212
[6] Spagnolo N, Vitelli C, Bentivegna M, Brod D J, Crespi A, Flamini F, Giacomini S, Milani G, Ramponi R, Mataloni P, Osellame R, Galvao E F, Sciarrino F 2014 Nat. Photon. 8 615
Google Scholar
[7] Wang H, He Y, Li Y H, Su Z E, Li B, Huang H L, Ding X, Chen M C, Liu C, Qin J, Li J P, He Y M, Schneider C, Kamp M, Peng C Z, Hofling S, Lu C Y, Pan J W 2017 Nat. Photon. 11 361
Google Scholar
[8] Plenio M 2009 Contemp. Phys. 50 337
Google Scholar
[9] Lloyd S 1995 Phys. Rev. Lett. 75 346
Google Scholar
[10] Monroe C, Meekhof D M, King B E, Itano W M, Wineland D J 1995 Phys. Rev. Lett. 75 4714
Google Scholar
[11] Clarke J, Wilhelm F K 2008 Nature 453 1031
Google Scholar
[12] Gershenfeld N A, Chuang I L 1997 Science 275 350
Google Scholar
[13] 孔祥宇, 朱垣晔, 闻经纬, 辛涛, 李可仁, 龙桂鲁 2018 67 220301
Google Scholar
Kong X Y, Zhu Y Y, Wen J W, Xin T, Li K R, Long G L 2018 Acta Phys. Sin. 67 220301
Google Scholar
[14] Loss D, DiVincenzo D P 1998 Phys. Rev. A 57 120
Google Scholar
[15] Tewari S, Das Sarma S, Nayak C, Zhang C W, Zoller P 2007 Phys. Rev. Lett. 98 010506
Google Scholar
[16] Yoran N, Reznik B 2003 Phys. Rev. Lett. 91 037903
Google Scholar
[17] Laing A, Peruzzo A, Politi A, Verde M R, Halder M, Ralph T C, Thompson M G, O'Brien J L 2010 Appl. Phys. Lett. 97 211109
Google Scholar
[18] Knill E, Laflamme R, Milburn G J 2001 Nature 409 46
Google Scholar
[19] Kok P, Munro W J, Nemoto K, Ralph T C, Dowling J P, Milburn G J 2007 Rev. Mod. Phys. 79 135
Google Scholar
[20] Zhang Q Y, Xu P, Zhu S N 2018 Chin. Phys. B 27 054207
Google Scholar
[21] Feng L T, Zhang M, Zhou Z Y, Li M, Xiong X, Yu L, Shi B S, Guo G P, Dai D X, Ren X F, Guo G C 2016 Nat. Commun. 7 11985
Google Scholar
[22] Marcikic I, de Riedmatten H, Tittel W, Zbinden H, Legre M, Gisin N 2004 Phys. Rev. Lett. 93 180502
Google Scholar
[23] Politi A, Cryan M J, Rarity J G, Yu S Y, O'Brien J L 2008 Science 320 646
Google Scholar
[24] Marshall G D, Politi A, Matthews J C F, Dekker P, Ams M, Withford M J, O'Brien J L 2009 Opt. Express 17 12546
Google Scholar
[25] Davis K M, Miura K, Sugimoto N, Hirao K 1996 Opt. Lett. 21 1729
Google Scholar
[26] Mattle K, Weinfurter H, Kwiat P G, Zeilinger A 1996 Phys. Rev. Lett. 76 4656
Google Scholar
[27] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2010 Phys. Rev. Lett. 105 200503
Google Scholar
[28] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[29] Crespi A, Ramponi R, Osellame R, Sansoni L, Bongioanni I, Sciarrino F, Vallone G, Mataloni P 2011 Nat. Commun. 2 566
Google Scholar
[30] Homoelle D, Wielandy S, Gaeta A L, Borrelli N F, Smith C 1999 Opt. Lett. 24 1311
Google Scholar
[31] Gattass R R, Mazur E 2008 Nat. Photon. 2 219
Google Scholar
[32] Della Valle G, Osellame R, Laporta P 2009 J. Opt. A: Pure Appl. Opt. 11 049801
Google Scholar
[33] Osellame R, Taccheo S, Marangoni M, Ramponi R, Laporta P, Polli D, de Silvestri S, Cerullo G 2003 J. Opt. Soc. Am. B: Opt. Phys. 20 1559
Google Scholar
[34] Eaton S M, Chen W, Zhang L, Zhang H, Iyer R, Aitchison J S, Herman P R 2006 IEEE Photon.Tech. L 18 2174
Google Scholar
[35] Osellame R, Hoekstra H J W M, Cerullo G, Pollnau M 2011 Laser Photon. Rev. 5 442
Google Scholar
[36] Itoh K, Watanabe W, Nolte S, Schaffer C B 2006 MRS Bull. 31 620
Google Scholar
[37] 魏伟华, 李木天, 刘墨南 2018 67 064203
Google Scholar
Wei W H, Li M T, Liu M N 2018 Acta Phys. Sin. 67 064203
Google Scholar
[38] Boada O, Novo L, Sciarrino F, Omar Y 2017 Phys. Rev. A 95 013830
Google Scholar
[39] Tang H, Lin X F, Feng Z, Chen J Y, Gao J, Sun K, Wang C Y, Lai P C, Xu X Y, Wang Y, Qiao L F, Yang A L, Jin X M 2018 Sci. Adv. 4 eaat3174
Google Scholar
[40] Crespi A, Osellame R, Ramponi R, Giovannetti V, Fazio R, Sansoni L, de Nicola F, Sciarrino F, Mataloni P 2013 Nat. Photon. 7 322
Google Scholar
[41] Spagnolo N, Vitelli C, Aparo L, Mataloni P, Sciarrino F, Crespi A, Ramponi R, Osellame R 2013 Nat. Commun. 4 1606
Google Scholar
[42] Tillmann M, Dakic B, Heilmann R, Nolte S, Szameit A, Walther P 2013 Nat. Photon. 7 540
Google Scholar
[43] Houck A A, Tureci H E, Koch J 2012 Nat. Phys. 8 292
Google Scholar
[44] Pitsios I, Banchi L, Rab A S, Bentivegna M, Caprara D, Crespi A, Spagnolo N, Bose S, Mataloni P, Osellame R, Sciarrino F 2017 Nat. Commun. 8 1569
Google Scholar
[45] Hong C K, Ou Z Y, Mandel L 1987 Phys. Rev. Lett. 59 2044
Google Scholar
[46] Meany T, Delanty M, Gross S, Marshall G D, Steel M J, Withford M J 2012 Opt. Express 20 26895
Google Scholar
[47] Chaboyer Z, Meany T, Helt L G, Withford M J, Steel M J 2015 Sci. Rep. 5 9601
Google Scholar
[48] Corrielli G, Atzeni S, Piacentini S, Pitsios I, Crespi A, Osellame R 2018 Opt. Express 26 15101
Google Scholar
[49] Pitsios I, Samara F, Corrielli G, Crespi A, Osellame R 2017 Sci. Rep. 7 11342
Google Scholar
[50] Fernandes L A, Grenier J R, Herman P R, Aitchison J S, Marques P V S 2012 Opt. Express 20 24103
Google Scholar
[51] Arriola A, Gross S, Jovanovic N, Charles N, Tuthill P G, Olaizola S M, Fuerbach A, Withford M J 2013 Opt. Express 21 2978
Google Scholar
[52] Chen G Y, Piantedosi F, Otten D, Kang Y Q, Zhang W Q, Zhou X H, Monro T M, Lancaster D G 2018 Sci. Rep. 8 10377
Google Scholar
[53] Zhang R C, Wang J M, Zhao G, Lü J Y 2013 Opt. Express 21 18434
Google Scholar
[54] Nasu Y, Kohtoku M, Hibino Y 2005 Opt. Lett. 30 723
Google Scholar
[55] Cheng Y, Sugioka K, Midorikawa K, Masuda M, Toyoda K, Kawachi M, Shihoyama K 2003 Opt. Lett. 28 55
Google Scholar
[56] Dekker P, Ams M, Marshall G D, Little D J, Withford M J 2010 Opt. Express 18 3274
Google Scholar
[57] Liu Z M, Liao Y, Wang Z H, Zhang Z H, Liu Z X, Qiao L L, Cheng Y 2018 Materials 11 1926
Google Scholar
[58] Heilmann R, Grafe M, Nolte S, Szameit A 2014 Sci. Rep. 4 4118
[59] Bhardwaj V R, Corkum P B, Rayner D M, Hnatovsky C, Simova E, Taylor R S 2004 Opt. Lett. 29 1312
Google Scholar
[60] Corrielli G, Crespi A, Geremia R, Ramponi R, Sansoni L, Santinelli A, Mataloni P, Sciarrino F, Osellame R 2014 Nat. Commun. 5 4249
Google Scholar
[61] Politi A, Matthews J C F, O'Brien J L 2009 Science 325 1221
Google Scholar
[62] Ralph T C, Langford N K, Bell T B, White A G 2002 Phys. Rev. A 65 062324
Google Scholar
[63] Hofmann H F, Takeuchi S 2002 Phys. Rev. A 66 024308
Google Scholar
[64] O'Brien J L, Pryde G J, White A G, Ralph T C, Branning D 2003 Nature 426 264
Google Scholar
[65] Yariv A 1973 IEEE J. Quantum Electron. 9 919
Google Scholar
[66] Pittman T B, Jacobs B C, Franson J D 2001 Phys. Rev. A 64 062311
Google Scholar
[67] Zeuner J, Sharma A N, Tillmann M, Heilmann R, Grafe M, Moqanaki A, Szameit A, Walther P 2018 Npj Quantum Inf. 4 13
Google Scholar
[68] Knill E 2002 Phys. Rev. A 66 052306
Google Scholar
[69] Meany T, Biggerstaff D N, Broome M A, Fedrizzi A, Delanty M, Steel M J, Gilchrist A, Marshall G D, White A G, Withford M J 2016 Sci. Rep. 6 25126
Google Scholar
[70] Zhang Q, Li M, Chen Y, Ren X, Osellame R, Gong Q, Li Y 2019 Opt. Mater. Express 9 2318
[71] Toffoli T 1980 Proceedings of the 7th Colloquium on Automata, Languages and Programming Berlin, Heidelberg, July 14–18, 1980 p632
[72] Cory D G, Price M D, Maas W, Knill E, Laflamme R, Zurek W H, Havel T F, Somaroo S S 1998 Phys. Rev. Lett. 81 2152
Google Scholar
[73] Shor P W 1997 SIAM J. Comput. 26 1484
Google Scholar
[74] Monz T, Kim K, Hansel W, Riebe M, Villar A S, Schindler P, Chwalla M, Hennrich M, Blatt R 2009 Phys. Rev. Lett. 102 040501
Google Scholar
[75] Fedorov A, Steffen L, Baur M, da Silva M P, Wallraff A 2012 Nature 481 170
Google Scholar
[76] Barenco A, Bennett C H, Cleve R, DiVincenzo D P, Margolus N, Shor P, Sleator T, Smolin J A, Weinfurter H 1995 Phys. Rev. A 52 3457
Google Scholar
[77] Adamatzky A 2002 Collision-Based Computing (London: Springer-Verlag) p120
[78] Nielsen M E, Nielsen M A, Chuang I L 2000 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press) p182
[79] Ralph T C, Resch K J, Gilchrist A 2007 Phys. Rev. A 75 022313
Google Scholar
[80] Lanyon B P, Barbieri M, Almeida M P, Jennewein T, Ralph T C, Resch K J, Pryde G J, O'Brien J L, Gilchrist A, White A G 2009 Nat. Phys. 5 134
Google Scholar
[81] Patel R B, Ho J, Ferreyrol F, Ralph T C, Pryde G J 2016 Sci. Adv. 2 e1501531
Google Scholar
[82] Ivanov S S, Ivanov P A, Vitanov N V 2015 Phys. Rev. A 91 032311
Google Scholar
[83] Zhu C H, Cao X, Quan D X, Pei C X 2014 Chin. Phys. B 23 084207
Google Scholar
[84] Wang H F, Zhang S, Zhu A D 2012 Chin. Phys. B 21 040306
Google Scholar
[85] Buhrman H, Cleve R, Watrous J, de Wolf R 2001 Phys. Rev. Lett. 87 167902
Google Scholar
[86] Hofmann H F 2012 Phys. Rev. Lett. 109 020408
Google Scholar
[87] Cernoch A, Soubusta J, Bartuskova L, Dusek M, Fiurasek J 2008 Phys. Rev. Lett. 100 180501
Google Scholar
[88] Fiurasek J 2008 Phys. Rev. A 78 032317
Google Scholar
[89] Ono T, Okamoto R, Tanida M, Hofmann H F, Takeuchi S 2017 Sci. Rep. 7 45353
Google Scholar
-
图 1 双光子HOM量子干涉示意图 (a)两个光子通过分束器后都透射和都反射的情况相干相消, 仅会出现一个光子透射而另一个光子反射的情况, 即光子成对的从分束器的任意一个输出端口离开; (b)在分束器两个输出端口对两个输出光子的符合计数值随两个光子进入分束器时的相对延时的变化曲线
Figure 1. Two-photon HOM quantum interference in a balanced beam splitter. (a) Destructive interference of two situations: both photons are transmitted and reflected. Only one photon is transmitted and the other photon is reflected. Photons leave in pairs from any of the beam splitter's output ports. (b) The coincidence counts of detecting a photon at each output of the splitter as a function of the relative delay of the photons.
图 2 基于波导的2 × 2集成定向耦合器示意图, 其中, d和L分别表示耦合区两个波导之间的间距和相互作用长度
Figure 2. Schematic of anintegrated DC consisting of two waveguides. Interaction distance and length in the coupling region are denoted by d and L, respectively.
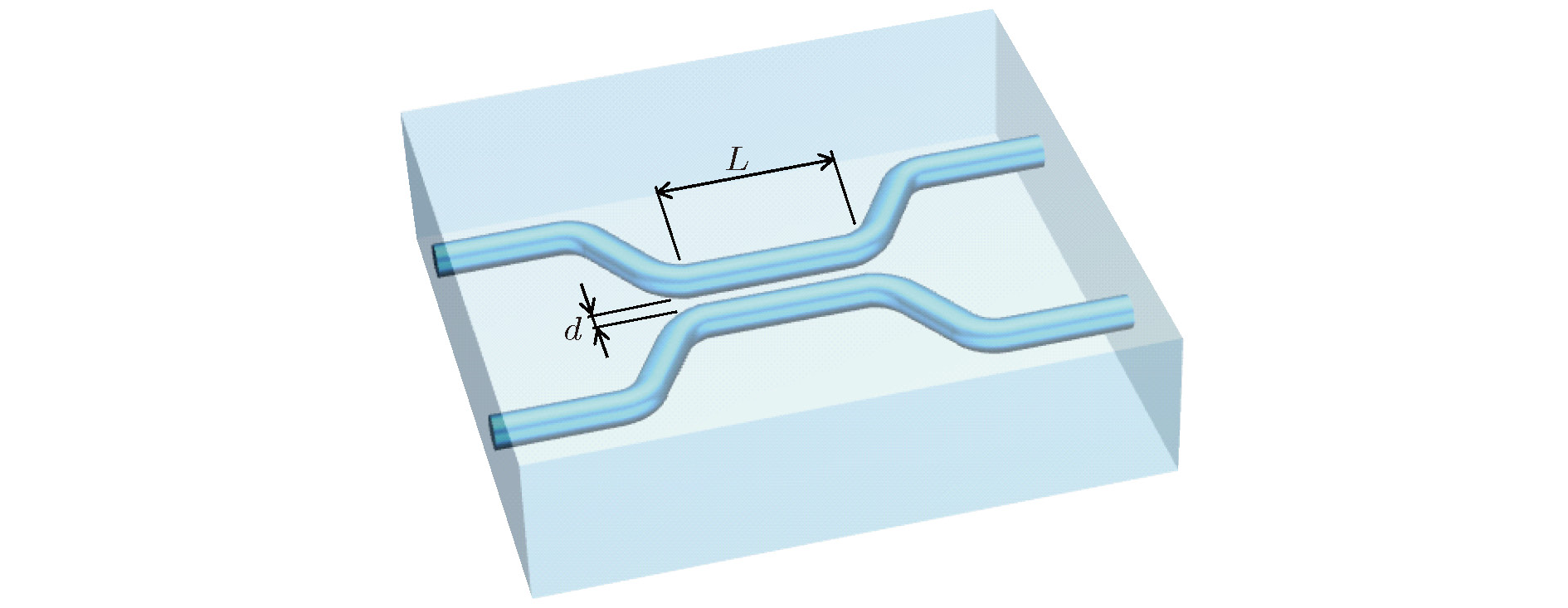
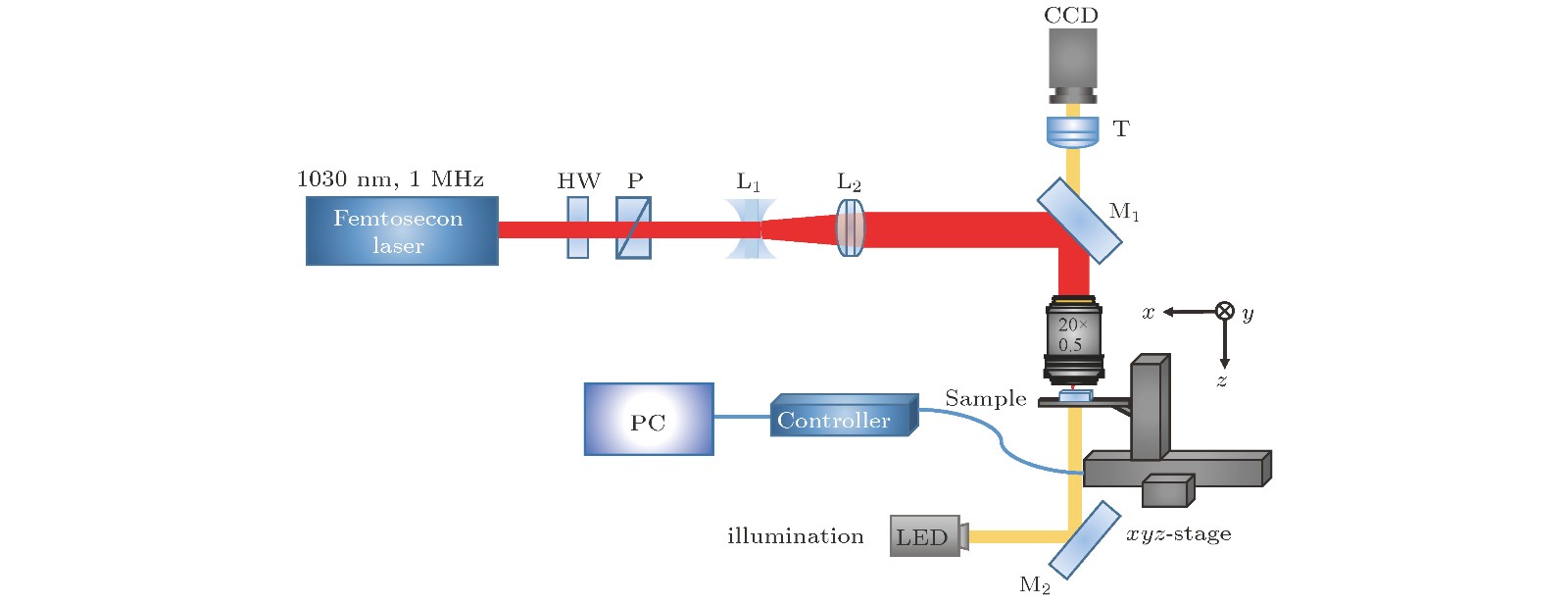
图 3 飞秒激光直写定向耦合器示意图和测得的HOM干涉曲线[24] (a)飞秒激光横向直写波导示意图; (b)飞秒激光在波导截面引起的折射率变化; (c)飞秒激光直写的定向耦合器阵列; (d)量子光源表征定向耦合器的实验装置; (e)双光子符合计数随光子间相对延迟差的变化曲线
Figure 3. Schematic of femtosecond laser direct writing of DCs based on waveguides and the coincident counts of detecting a photon at each output of the coupler as a function of the relative delay in arrival time of the photons[24]; (a) Femtosecond laser transverse writing of waveguides; (b) femtosecond laser induced refractive index change at the cross section of the waveguide; (c) femtosecond laser written DC array; (d) experimental setup for quantum characterization of DCs; (e) the coincident counts of detecting a photon at each output of the coupler as a function of the relative delay in arrival time of the photons.
图 4 可调谐三端口干涉仪(a)和不同相移量θ值下, 干涉仪输出端口两光子符合计数值随两光子进入干涉仪时的相对延迟差的变化曲线(b)[47]
Figure 4. Schematic ofa tunable 3D multi-path interferometer (a) and the coincident countsof detecting photons at outputs of the interferometer under different phase shift θ as a function of the relative delay in arrival time of the photons (b)[47]. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.
图 5 双折射补偿法制备偏振不敏感的定向耦合器[48] (a)飞秒激光直写定向耦合器示意图, 第二根写入的波导的双折射会受到第一根写入的波导的影响; (b)利用不同的加工参数在第二根波导旁边写入一根损伤线, 可以平衡两根波导的双折射; (c), (d)定向耦合器耦合区域分别在加写损伤线之前和之后的显微镜图, 损伤线距离第二根波导32 μm, 图中标尺为20 μm; (e), (f)对角线偏振光入射时, 定向耦合器输出态分别在加写损伤线之前和之后的斯托克斯分量; (g)光从m波导入射, 从n波导出射时, 在水平偏振和垂直偏振分量之间获得了相移φm→n; (h)相移φm→n随损伤线距离的变化曲线, 当距离为32 μm时, 四种情况下的φm→n一致
Figure 5. Polarization-independent DC based on local birefringence engineering[48]: (a) Schematic of a femtosecond written DC, the birefringence of the second waveguide is modified by the previously inscribed first one; (b) an additional damage track, with tuned irradiation parameters, is inscribed next to the second waveguide, leading to birefringence equalization; (c), (d) microscope images of the interaction region of the DCs without and with the inscription of the additional track at a distance of 32 μm, scale bar is 20 μm; (e), (f) Stokes parameters of the output states for couplers without and with the additional track, for diagonally polarized input light and various input-output combinations. A planar projection of the Poincaré sphere is represented; (g) light that enters in waveguide m and exits from waveguide n acquires a phase shift φm→n between the horizontally and the vertically polarized components; (h) the different values of φm→n are plotted as a function of distance of the track from the second waveguide. For a distance of 32 μm, the four possible φm→n coincide.
图 6 飞秒激光加工光量子逻辑门实验装置图
Figure 6. Experimental setup for femtosecond laser fabrication of photonic quantum logic gates.
图 7 波导截面形貌显微图(a)和在808 nm波长处的导光模式(b)
Figure 7. Microscope image of the cross section of the waveguide (a) and the near field image of the waveguide guided mode at 808 nm (b).
图 8 50 : 50分束比定向耦合器在808 nm波长处的导光模式(a)和测得的HOM干涉曲线(b), 干涉可见度约为 0.98
Figure 8. The near field image of the DC guided mode at 808 nm (a) and the coincidence counts of detecting photons at outputs of the DC as a function of the relative delay the photons(b), the visibility is ~ 0.98.
图 9 压力场调控波导双折射来获得特定的波片操作[58] (a)波导旁边附加写入的破坏线通过压力场改变波导光轴的取向; (b)飞秒激光直写三组不同相对位置破坏线示意图; (c)为波导光轴取向角α随破坏线相对位置取向角θ的变化曲线
Figure 9. Settings of reorientation of the optical axis through stress fields and measured wave plate operations[58]: (a) Schematic of the cross section of the waveguide arrangement where additional stress fields induce a reorientation of the waveguide’s optical axis; (b) sketch of the writing setting, with which the quantum gates are fabricated (here for 3 different orientations of the defect relatively to the waveguide); (c) experimental data and best fit model of the reorientation of the optical axis α as a function of the azimuthal position of the defect θ. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.
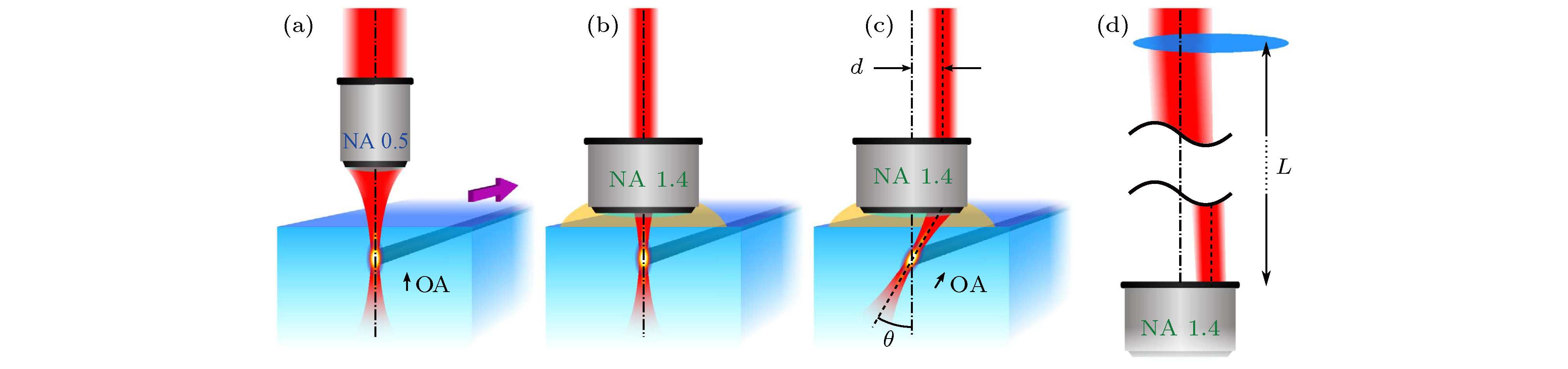
图 10 直写光倾斜入射调控波导光轴方向示意图[60] (a)直写激光正入射充满低数值孔径物镜, 产生的双折射波导光轴OA沿激光传播方向分布; (b)直写激光正入射未充满高数值孔径物镜可以带来和图(a)相同的效果; (c)直写激光偏移距离d后入射高数值孔径物镜使得激光在样品体内旋转θ角度, 波导光轴也随之旋转相同角度, θ取决于d; (d)通过在物镜前L距离处放置长焦透镜可实现直写激光的偏移和缩束
Figure 10. Conceptual scheme of the method enabling the direct writing of optical waveguides acting as integrated wave plates with tilted axis[60]: (a) Traditional writing scheme adopting a focusing objective with moderate NA; the symmetry of the writing layout creates birefringent waveguides with the optical axis (OA) aligned as the writing beam direction; actual waveguide writing is performed by a transverse translation of the glass sample (indicated by the purple arrow); (b) equivalent waveguides can be created by underfilling a high-NA oil-immersion objective; (c) offsetting the writing beam before the objective results in waveguide writing with an inclined laser beam; the resulting waveguide has an optical axis tilted by an angle θ that depends on the amount of offset d of the writing beam with respect to the objective axis; (d) reduced beam size and offset at the objective aperture is achieved by a small transverse shift of a long focal lens placed at a distance L from the focusing objective.
图 11 路径编码量子比特的H门
Figure 11. Schematic of a path-encoded qubit H gate.
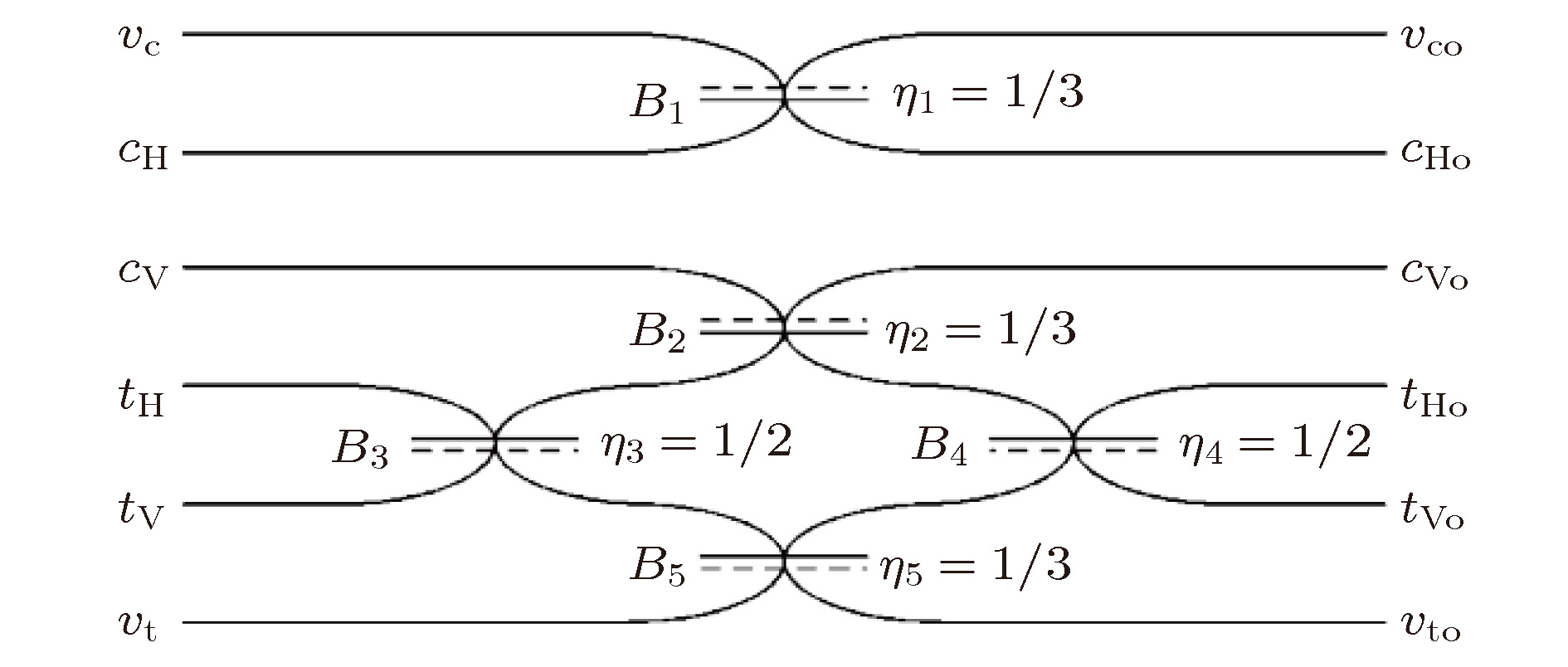
图 12 路径编码量子比特的CNOT门结构图[62] 虚线表示定向耦合器中附加相位
${\text{π}}$ 的反射面; 路径cH和cV代表控制比特, 路径tH和tV代表目标比特, 路径vc和vt代表不会被占据的辅助比特; 图中数字表示对应定向耦合器的反射率Figure 12. Schematic of a path-encoded qubit CNOT gate based on waveguides[62]. Dashed line indicates the surface from which a sign change occurs upon reflection in a DC. The control modes are cH and cV. The target modes are tH and tV. The modes vc and vt are unoccupied ancillary modes. The numbers indicate the reflectivity of the corresponding directional coupler.
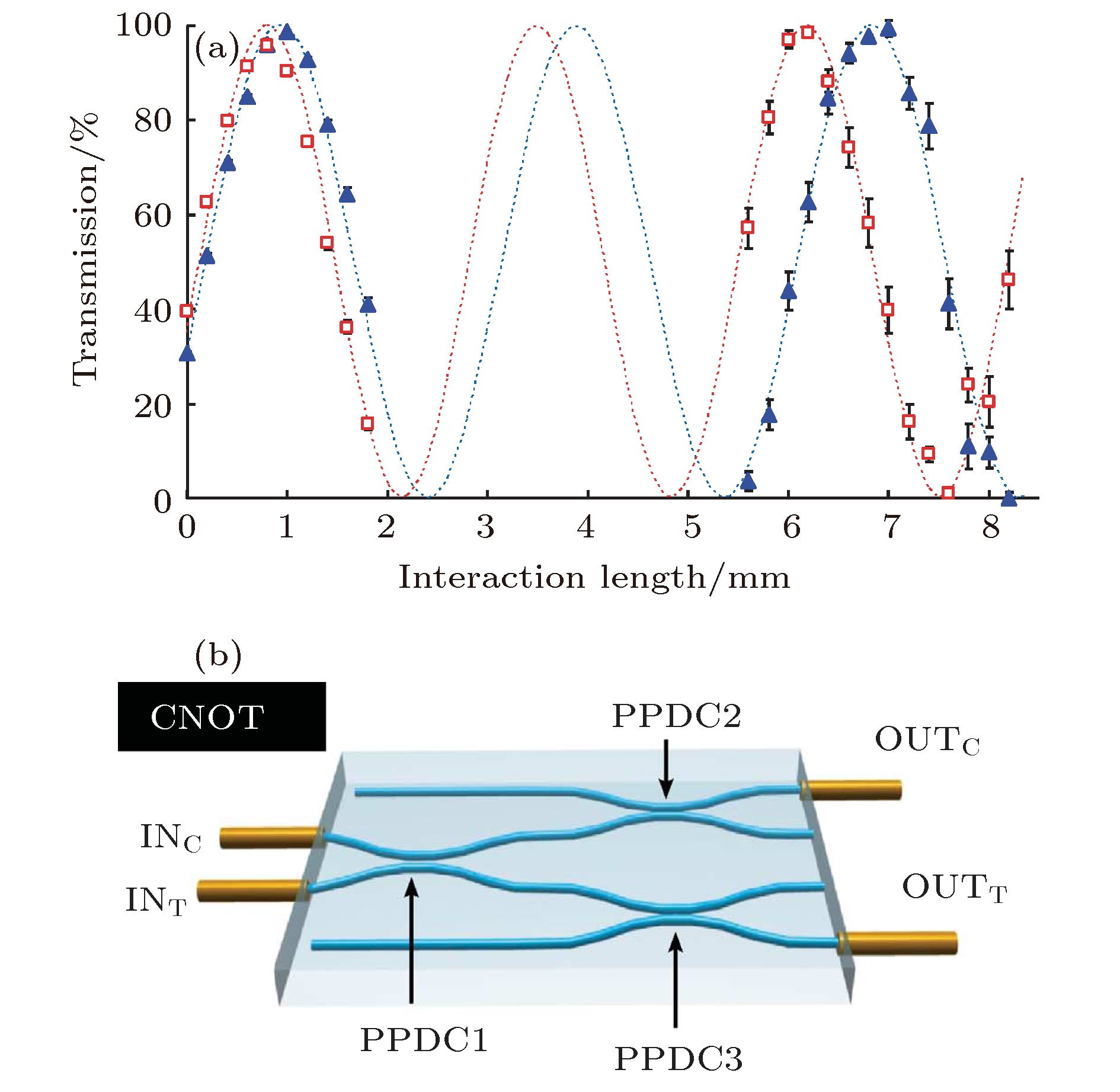
图 13 部分偏振定向耦合器中两种偏振态的耦合区能量交换振荡曲线(方块代表H态, 三角代表V态)(a)和偏振编码量子比特的CNOT门波导结构图(b)[29]
Figure 13. H (squares) and V (triangles) polarization transmissions of DCs with different interaction lengths, based on slightly birefringent waveguides (a) and schematic of a polarization-encoded qubit CNOT gate based on PPDCs (b)[29].
图 14 纠缠态辅助光子的偏振编码可预报式CNOT门结构图(a)和量子性能表征实验装置示意图(b)[67]
Figure 14. (a) Scheme of a heralded photonic CNOT gate using a maximally entangled ancilla state with improved success probability 1/4. Detection of one photon in each of the modes
$a_{out}^1$ and$a_{out}^2$ heralds successful gate operation. (b) Experimental setup for quantum characterization of the polarization-encoded qubit heralded CNOT gate[67]. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.
图 15 路径编码的hCZ门结构图[69] (a)路径C0 (T0)代表|0〉态, 不与其他态相互作用, C (T)代表|1〉态, A和B代表辅助光子态, 它们通过四个定向耦合器相互作用, 耦合器反射率R(θn) = cos2(θn), 图中浅色面代表附加
${\text{π}}$ 相位的反射面; (b)由四条立体交叉波导路经构成的hCZ门结构Figure 15. Schematic of a path-encoded qubit hCZ gate[69]. (a) The circuit for a hCZ gate showing paths for ancillary photons A and B as well as the computational qubits; the control (target) photon is encoded across spatial paths C0 (T0) representing |0〉 and C (T) representing |1〉. The |0〉 modes do not interact in the gate; the four remaining modes undergo four DCs operations with reflectivities R(θn) = cos2(θn). The light-coloured side indicates the surface yielding a relative
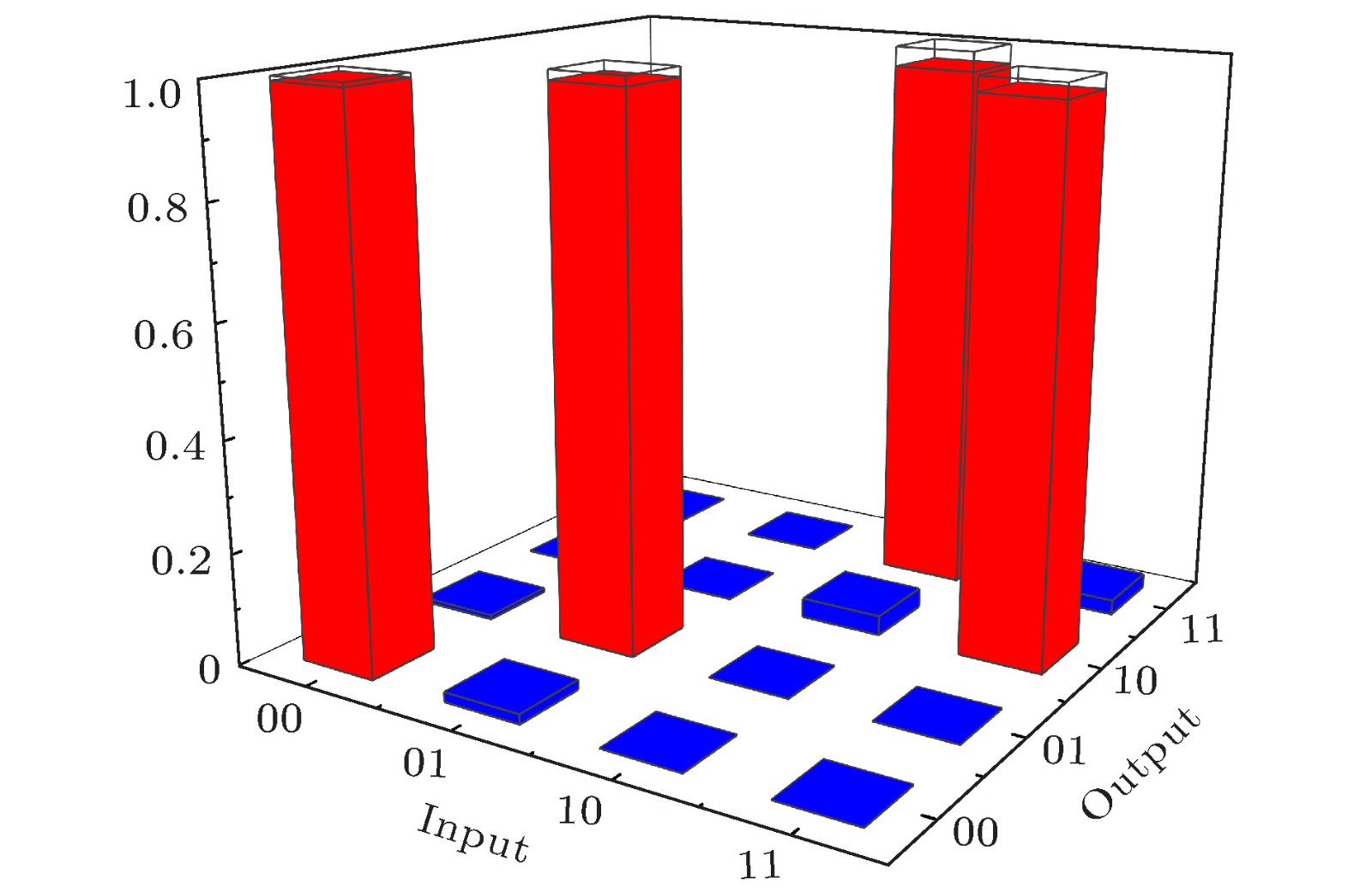
${\text{π}}$ phase change upon reflection. (b) The four interacting circuit modes modelled as a waveguide array, showing the crossover and optimal reflectivities for the DCs implemented using evanescent coupling. Copyright: http://creativecommons.org/licenses/by/4.0/ for CC BY.
图 16 根据实验实测值构建的真值表柱状图, 保真度约为0.98
Figure 16. Experimentally constructed CNOT logical truth table. The labels on the Input and Output axes identify the state |C, T〉. Ideally, a flip of the logical state of the target qubit (T) occurs only when the control qubit (C) is in the logical |1〉 state. The fidelity of the gate is ~ 0.98.
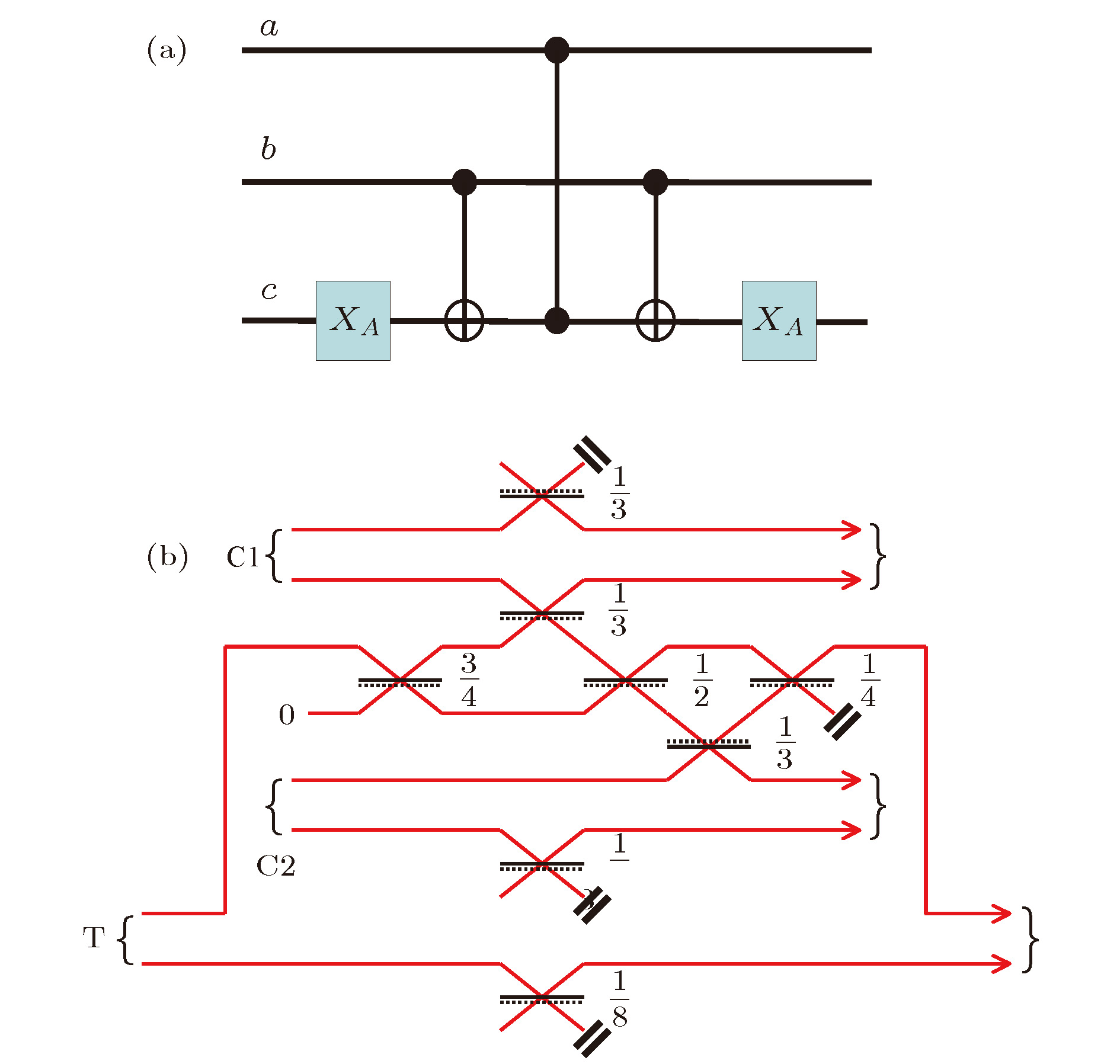
图 17 控制比特(a, b)为qubit、目标比特(c)为qutrit(
$\left| 0 \right\rangle $ ,$\left| 1 \right\rangle $ 和$\left| 2 \right\rangle $ 态)的Toffoli门方案(a)和基于波导路径的线性光学实现方案(b)[79] (a)中, 当目标比特处于第三态|2〉态时, 前后两个CNOT门中间的CZ门操作逻辑和正常两态量子比特系统相同, XA单比特逻辑门的作用是实现|0〉和|2〉态之间的翻转; (b)中, 每个控制比特由两条波导路径表示, 目标比特则由三条波导路径表示, 图中标记为0的路径代表第三态; 当且仅当三个量子比特的上面那条路径被占据时, 输出态发生相位翻转, 即使实现Toffoli相位门操作Figure 17. (a) Realization of aToffoli gate using two qubits (a and b) and a qutrit (c). CNOT gates (first andlast two-qubit gates) operate as normal on the qubit levels andimplement the identity if the target is in the qutrit level (|2〉). Similarly for the CZ gate (middle two-qubit gate). The XA gate flips thequtrit between the states |0〉 and |2〉. The sign change occurs on the|1,0,1〉 component. (b) A nondeterministic, post-selected, opticalrealization of a Toffoli gate[79]. Each input qubit is represented bytwo modes (waveguide paths). An additional target mode is introduced in the central part of the diagram. DCs are represented as black lines with their reflectivity indicated to the right. A phase flip occurs by reflection off the surface indicated by a dotted line. If we take occupation of the top mode of each qubit to represent logical |0〉 and occupation of the bottom mode to represent logical |1〉, then the circuit implements a Toffoli gate in which a phase flip is only applied to the element |000〉.
图 18 利用体光学元件在自由空间中实现Toffoli门的实验装置[80] (a)逻辑线路图, 采用|H〉偏振和|V〉偏振编码量子比特的|0〉态和|1〉态两个状态, 通过偏振分束器PBS1扩展出一条额外的路径b, 从而将目标比特从两态系统扩展到四态系统, 即|H, t〉, |H, b〉, |V, t〉和|V, b〉四种状态, 下路径b绕过了后面两个两比特逻辑门; 当在探测器D1上探测到一个光子时, Toffoli门操作成功; (b), (c)实验装置; PPBS, 部分偏振分束器; SPCM, 单光子计数模块; PDC, 参量下转换; SHG, 二次谐波产生
Figure 18. Toffoli and controlled-unitary experimental layout[80]. (a) Conceptual logic circuit. A polarizing beam splitter temporarily expands the Hilbert space of the target information carrier, from a polarization-encoded photonic qubit to a multi-level system distributed across polarization and longitudinal spatial mode. Information in the bottom rail (b) bypasses the two-qubit gates. Detection of a photon at D1 heralds a successful implementation; (b), (c) Experimental circuit and optical source. An inherently stable polarization interferometer using two calcite beam displacers is used. PPBS, partially polarizing beam splitter; SPCM, single-photon counting module; PDC, parametric down conversion; SHG, second-harmonic generation.
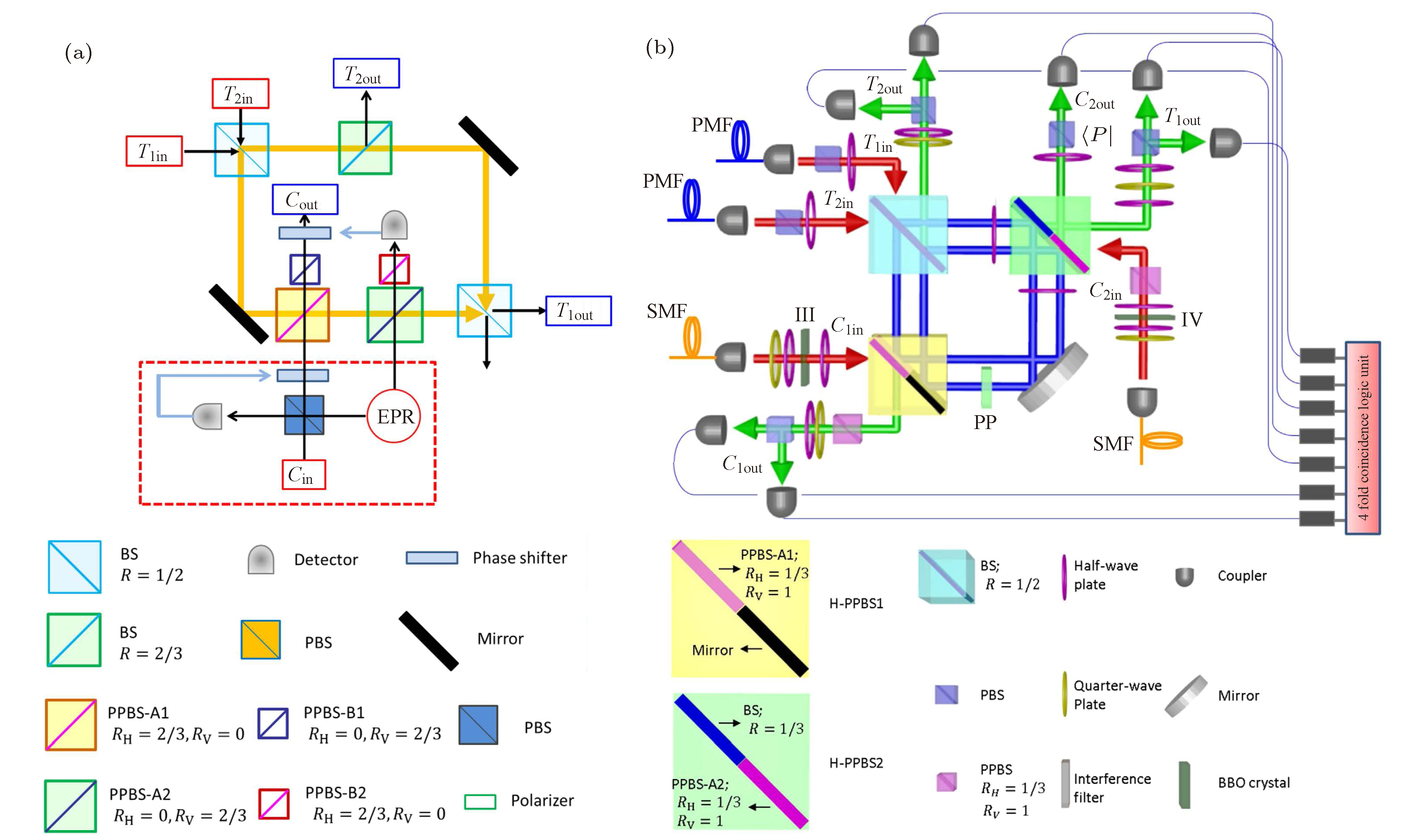
图 19 利用体光学元件在自由空间中实现Fredkin门的两种实验方案 (a)早期实验方案, 控制比特态决定相位门的相位变化, 该相位门两个CNOT门构成, CNOT操作基于部分偏振分束器上的双光子干涉实现, 入射到两个CNOT门的两光子态编码控制比特输入态, 使其从非纠缠的
$\left( {\alpha {{\left| H \right\rangle }_{{C_{in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}} \right)/\sqrt 2 $ 态以1/2的概率转化为$\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $ 纠缠态; (b)简化的实验方案, 控制比特态直接制备于$\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $ 纠缠态上, 当在输出端口(T1out, T2out, C1out, C2out)同时探测到光子时代表门操作成功, 概率为1/162; BS, 分束器; PBS, 偏振分束器; PPBS, 部分偏振分束器; Detector, 探测器; Phaseshifter, 相移器; Mirror, 反射镜; Polarizer, 偏振片; Half-wave plate, 半波片; Quarter-wave plate, 四分之一波片; Interferencefilter, 干涉滤波片; BBO crystal, BBO晶体[88, 89]Figure 19. Two kinds of free-space experimental layouts for Fredkin gate. (a) Original proposal by Fiurášek. The phase of the quantum phase gate (QPG) is changed by a control qubit: φ = 0 (
${\text{π}}$ ) when the control qubit is |0〉(|1〉). The QPG is realized by combining two CNOT gates, which are based on the two-photon interferences at the partially polarizingbeam splitters. The state of the control qubit is encoded into the state of the two photons incident to the CNOT gates by using an Einstein-Podolsky-Rosen (EPR) source and a quantum parity check: the encoder transforms the input state of the control photon$\left( {\alpha {{\left| H \right\rangle }_{{C_{in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}} \right)/\sqrt 2 $ into a state$\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $ with a probability of 1/2. (b) Simplifed scheme. The control qubit is directly encoded into the entangled photon pair$\left( {\alpha {{\left| H \right\rangle }_{{C_{1in}}}}{{\left| V \right\rangle }_{{C_{2in}}}} + \beta {{\left| V \right\rangle }_{{C_{in}}}}{{\left| H \right\rangle }_{{C_{2in}}}}} \right)/\sqrt 2 $ generated via spontaneous parametric down-conversion and local polarization operations. The Fredkin operation is successful when the photons are simultaneously detected at the output ports (T1out, T2out, C1out, C2out) with a success probability of 1/162[88, 89]. -
[1] Bennett C H 1995 Phys. Today 48 24
[2] Galindo A, Martin-Delgado M A 2002 Rev. Mod. Phys. 74 347
Google Scholar
[3] 范桁 2018 67 120301
Google Scholar
Fan H 2018 Acta Phys. Sin. 67 120301
Google Scholar
[4] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[5] Grover L K 1996 Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing Philadelphia, PA, USA, May 22 – 24, 1996 p212
[6] Spagnolo N, Vitelli C, Bentivegna M, Brod D J, Crespi A, Flamini F, Giacomini S, Milani G, Ramponi R, Mataloni P, Osellame R, Galvao E F, Sciarrino F 2014 Nat. Photon. 8 615
Google Scholar
[7] Wang H, He Y, Li Y H, Su Z E, Li B, Huang H L, Ding X, Chen M C, Liu C, Qin J, Li J P, He Y M, Schneider C, Kamp M, Peng C Z, Hofling S, Lu C Y, Pan J W 2017 Nat. Photon. 11 361
Google Scholar
[8] Plenio M 2009 Contemp. Phys. 50 337
Google Scholar
[9] Lloyd S 1995 Phys. Rev. Lett. 75 346
Google Scholar
[10] Monroe C, Meekhof D M, King B E, Itano W M, Wineland D J 1995 Phys. Rev. Lett. 75 4714
Google Scholar
[11] Clarke J, Wilhelm F K 2008 Nature 453 1031
Google Scholar
[12] Gershenfeld N A, Chuang I L 1997 Science 275 350
Google Scholar
[13] 孔祥宇, 朱垣晔, 闻经纬, 辛涛, 李可仁, 龙桂鲁 2018 67 220301
Google Scholar
Kong X Y, Zhu Y Y, Wen J W, Xin T, Li K R, Long G L 2018 Acta Phys. Sin. 67 220301
Google Scholar
[14] Loss D, DiVincenzo D P 1998 Phys. Rev. A 57 120
Google Scholar
[15] Tewari S, Das Sarma S, Nayak C, Zhang C W, Zoller P 2007 Phys. Rev. Lett. 98 010506
Google Scholar
[16] Yoran N, Reznik B 2003 Phys. Rev. Lett. 91 037903
Google Scholar
[17] Laing A, Peruzzo A, Politi A, Verde M R, Halder M, Ralph T C, Thompson M G, O'Brien J L 2010 Appl. Phys. Lett. 97 211109
Google Scholar
[18] Knill E, Laflamme R, Milburn G J 2001 Nature 409 46
Google Scholar
[19] Kok P, Munro W J, Nemoto K, Ralph T C, Dowling J P, Milburn G J 2007 Rev. Mod. Phys. 79 135
Google Scholar
[20] Zhang Q Y, Xu P, Zhu S N 2018 Chin. Phys. B 27 054207
Google Scholar
[21] Feng L T, Zhang M, Zhou Z Y, Li M, Xiong X, Yu L, Shi B S, Guo G P, Dai D X, Ren X F, Guo G C 2016 Nat. Commun. 7 11985
Google Scholar
[22] Marcikic I, de Riedmatten H, Tittel W, Zbinden H, Legre M, Gisin N 2004 Phys. Rev. Lett. 93 180502
Google Scholar
[23] Politi A, Cryan M J, Rarity J G, Yu S Y, O'Brien J L 2008 Science 320 646
Google Scholar
[24] Marshall G D, Politi A, Matthews J C F, Dekker P, Ams M, Withford M J, O'Brien J L 2009 Opt. Express 17 12546
Google Scholar
[25] Davis K M, Miura K, Sugimoto N, Hirao K 1996 Opt. Lett. 21 1729
Google Scholar
[26] Mattle K, Weinfurter H, Kwiat P G, Zeilinger A 1996 Phys. Rev. Lett. 76 4656
Google Scholar
[27] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2010 Phys. Rev. Lett. 105 200503
Google Scholar
[28] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[29] Crespi A, Ramponi R, Osellame R, Sansoni L, Bongioanni I, Sciarrino F, Vallone G, Mataloni P 2011 Nat. Commun. 2 566
Google Scholar
[30] Homoelle D, Wielandy S, Gaeta A L, Borrelli N F, Smith C 1999 Opt. Lett. 24 1311
Google Scholar
[31] Gattass R R, Mazur E 2008 Nat. Photon. 2 219
Google Scholar
[32] Della Valle G, Osellame R, Laporta P 2009 J. Opt. A: Pure Appl. Opt. 11 049801
Google Scholar
[33] Osellame R, Taccheo S, Marangoni M, Ramponi R, Laporta P, Polli D, de Silvestri S, Cerullo G 2003 J. Opt. Soc. Am. B: Opt. Phys. 20 1559
Google Scholar
[34] Eaton S M, Chen W, Zhang L, Zhang H, Iyer R, Aitchison J S, Herman P R 2006 IEEE Photon.Tech. L 18 2174
Google Scholar
[35] Osellame R, Hoekstra H J W M, Cerullo G, Pollnau M 2011 Laser Photon. Rev. 5 442
Google Scholar
[36] Itoh K, Watanabe W, Nolte S, Schaffer C B 2006 MRS Bull. 31 620
Google Scholar
[37] 魏伟华, 李木天, 刘墨南 2018 67 064203
Google Scholar
Wei W H, Li M T, Liu M N 2018 Acta Phys. Sin. 67 064203
Google Scholar
[38] Boada O, Novo L, Sciarrino F, Omar Y 2017 Phys. Rev. A 95 013830
Google Scholar
[39] Tang H, Lin X F, Feng Z, Chen J Y, Gao J, Sun K, Wang C Y, Lai P C, Xu X Y, Wang Y, Qiao L F, Yang A L, Jin X M 2018 Sci. Adv. 4 eaat3174
Google Scholar
[40] Crespi A, Osellame R, Ramponi R, Giovannetti V, Fazio R, Sansoni L, de Nicola F, Sciarrino F, Mataloni P 2013 Nat. Photon. 7 322
Google Scholar
[41] Spagnolo N, Vitelli C, Aparo L, Mataloni P, Sciarrino F, Crespi A, Ramponi R, Osellame R 2013 Nat. Commun. 4 1606
Google Scholar
[42] Tillmann M, Dakic B, Heilmann R, Nolte S, Szameit A, Walther P 2013 Nat. Photon. 7 540
Google Scholar
[43] Houck A A, Tureci H E, Koch J 2012 Nat. Phys. 8 292
Google Scholar
[44] Pitsios I, Banchi L, Rab A S, Bentivegna M, Caprara D, Crespi A, Spagnolo N, Bose S, Mataloni P, Osellame R, Sciarrino F 2017 Nat. Commun. 8 1569
Google Scholar
[45] Hong C K, Ou Z Y, Mandel L 1987 Phys. Rev. Lett. 59 2044
Google Scholar
[46] Meany T, Delanty M, Gross S, Marshall G D, Steel M J, Withford M J 2012 Opt. Express 20 26895
Google Scholar
[47] Chaboyer Z, Meany T, Helt L G, Withford M J, Steel M J 2015 Sci. Rep. 5 9601
Google Scholar
[48] Corrielli G, Atzeni S, Piacentini S, Pitsios I, Crespi A, Osellame R 2018 Opt. Express 26 15101
Google Scholar
[49] Pitsios I, Samara F, Corrielli G, Crespi A, Osellame R 2017 Sci. Rep. 7 11342
Google Scholar
[50] Fernandes L A, Grenier J R, Herman P R, Aitchison J S, Marques P V S 2012 Opt. Express 20 24103
Google Scholar
[51] Arriola A, Gross S, Jovanovic N, Charles N, Tuthill P G, Olaizola S M, Fuerbach A, Withford M J 2013 Opt. Express 21 2978
Google Scholar
[52] Chen G Y, Piantedosi F, Otten D, Kang Y Q, Zhang W Q, Zhou X H, Monro T M, Lancaster D G 2018 Sci. Rep. 8 10377
Google Scholar
[53] Zhang R C, Wang J M, Zhao G, Lü J Y 2013 Opt. Express 21 18434
Google Scholar
[54] Nasu Y, Kohtoku M, Hibino Y 2005 Opt. Lett. 30 723
Google Scholar
[55] Cheng Y, Sugioka K, Midorikawa K, Masuda M, Toyoda K, Kawachi M, Shihoyama K 2003 Opt. Lett. 28 55
Google Scholar
[56] Dekker P, Ams M, Marshall G D, Little D J, Withford M J 2010 Opt. Express 18 3274
Google Scholar
[57] Liu Z M, Liao Y, Wang Z H, Zhang Z H, Liu Z X, Qiao L L, Cheng Y 2018 Materials 11 1926
Google Scholar
[58] Heilmann R, Grafe M, Nolte S, Szameit A 2014 Sci. Rep. 4 4118
[59] Bhardwaj V R, Corkum P B, Rayner D M, Hnatovsky C, Simova E, Taylor R S 2004 Opt. Lett. 29 1312
Google Scholar
[60] Corrielli G, Crespi A, Geremia R, Ramponi R, Sansoni L, Santinelli A, Mataloni P, Sciarrino F, Osellame R 2014 Nat. Commun. 5 4249
Google Scholar
[61] Politi A, Matthews J C F, O'Brien J L 2009 Science 325 1221
Google Scholar
[62] Ralph T C, Langford N K, Bell T B, White A G 2002 Phys. Rev. A 65 062324
Google Scholar
[63] Hofmann H F, Takeuchi S 2002 Phys. Rev. A 66 024308
Google Scholar
[64] O'Brien J L, Pryde G J, White A G, Ralph T C, Branning D 2003 Nature 426 264
Google Scholar
[65] Yariv A 1973 IEEE J. Quantum Electron. 9 919
Google Scholar
[66] Pittman T B, Jacobs B C, Franson J D 2001 Phys. Rev. A 64 062311
Google Scholar
[67] Zeuner J, Sharma A N, Tillmann M, Heilmann R, Grafe M, Moqanaki A, Szameit A, Walther P 2018 Npj Quantum Inf. 4 13
Google Scholar
[68] Knill E 2002 Phys. Rev. A 66 052306
Google Scholar
[69] Meany T, Biggerstaff D N, Broome M A, Fedrizzi A, Delanty M, Steel M J, Gilchrist A, Marshall G D, White A G, Withford M J 2016 Sci. Rep. 6 25126
Google Scholar
[70] Zhang Q, Li M, Chen Y, Ren X, Osellame R, Gong Q, Li Y 2019 Opt. Mater. Express 9 2318
[71] Toffoli T 1980 Proceedings of the 7th Colloquium on Automata, Languages and Programming Berlin, Heidelberg, July 14–18, 1980 p632
[72] Cory D G, Price M D, Maas W, Knill E, Laflamme R, Zurek W H, Havel T F, Somaroo S S 1998 Phys. Rev. Lett. 81 2152
Google Scholar
[73] Shor P W 1997 SIAM J. Comput. 26 1484
Google Scholar
[74] Monz T, Kim K, Hansel W, Riebe M, Villar A S, Schindler P, Chwalla M, Hennrich M, Blatt R 2009 Phys. Rev. Lett. 102 040501
Google Scholar
[75] Fedorov A, Steffen L, Baur M, da Silva M P, Wallraff A 2012 Nature 481 170
Google Scholar
[76] Barenco A, Bennett C H, Cleve R, DiVincenzo D P, Margolus N, Shor P, Sleator T, Smolin J A, Weinfurter H 1995 Phys. Rev. A 52 3457
Google Scholar
[77] Adamatzky A 2002 Collision-Based Computing (London: Springer-Verlag) p120
[78] Nielsen M E, Nielsen M A, Chuang I L 2000 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press) p182
[79] Ralph T C, Resch K J, Gilchrist A 2007 Phys. Rev. A 75 022313
Google Scholar
[80] Lanyon B P, Barbieri M, Almeida M P, Jennewein T, Ralph T C, Resch K J, Pryde G J, O'Brien J L, Gilchrist A, White A G 2009 Nat. Phys. 5 134
Google Scholar
[81] Patel R B, Ho J, Ferreyrol F, Ralph T C, Pryde G J 2016 Sci. Adv. 2 e1501531
Google Scholar
[82] Ivanov S S, Ivanov P A, Vitanov N V 2015 Phys. Rev. A 91 032311
Google Scholar
[83] Zhu C H, Cao X, Quan D X, Pei C X 2014 Chin. Phys. B 23 084207
Google Scholar
[84] Wang H F, Zhang S, Zhu A D 2012 Chin. Phys. B 21 040306
Google Scholar
[85] Buhrman H, Cleve R, Watrous J, de Wolf R 2001 Phys. Rev. Lett. 87 167902
Google Scholar
[86] Hofmann H F 2012 Phys. Rev. Lett. 109 020408
Google Scholar
[87] Cernoch A, Soubusta J, Bartuskova L, Dusek M, Fiurasek J 2008 Phys. Rev. Lett. 100 180501
Google Scholar
[88] Fiurasek J 2008 Phys. Rev. A 78 032317
Google Scholar
[89] Ono T, Okamoto R, Tanida M, Hofmann H F, Takeuchi S 2017 Sci. Rep. 7 45353
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 13841
- PDF Downloads: 315
- Cited By: 0
