固态单自旋量子控制研究进展

李廷伟; 荣星; 杜江峰

doi:10.7498/aps.71.20211808

摘要

在量子物理领域的研究中, 量子控制是必不可少的. 精确高效的量子控制, 是利用量子系统进行实验研究的前提, 也是量子计算、量子传感等应用的基础. 金刚石氮-空位色心作为固态自旋体系在室温下相干时间长, 可用光学方法实现初始化和读出, 通过微波射频场能实现普适的量子控制, 是研究量子物理的优秀实验平台. 本文从量子控制出发介绍金刚石氮-空位色心体系在量子物理领域取得的代表性成果, 主要讨论了1) 金刚石氮-空位色心的物理性质和量子控制原理, 2)氮-空位色心的退相干机制, 3)单自旋量子控制的相关应用及最近的研究进展.

关键词:

Abstract

In the field of quantum physics, quantum control is essential. Precise and efficient quantum control is a prerequisite for the experimental research using quantum systems, and it is also the basis for applications such as in quantum computing and quantum sensing. As a solid-state spin system, the nitrogen-vacancy (NV) center in diamond has a long coherence time at room temperature. It can be initialized and read out by optical methods, and can achieve universal quantum control through the microwave field and radio frequency fields. It is an excellent experimental platform for studying quantum physics. In this review, we introduce the recent results of quantum control in NV center and discuss the following parts: 1) the physical properties of the NV center and the realization method of quantum control, 2) the decoherence mechanism of the NV center spin qubit, and 3) the application of single-spin quantum control and relevant research progress.

Keywords:

作者及机构信息

1.
中国科学技术大学, 中国科学院微观磁共振重点实验室和物理学院, 合肥　230026

2.
中国科学技术大学, 中国科学院量子信息与量子科技创新研究院, 合肥　230026

通信作者: 荣星, xrong@ustc.edu.cn

Authors and contacts

1.
CAS Key Laboratory of Microscale Magnetic Resonance and School of Physical Sciences, University of Science and Technology of China, Hefei 230026, China

2.
CAS Center for Excellence in Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei 230026, China

Corresponding author: Rong Xing, xrong@ustc.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Kastner M A 1992 Rev. Mod. Phys. 64 849 Google Scholar
[2]	Yoneda J, Takeda K, Otsuka T, Nakajima T, Delbecq M R, Allison G, Honda T, Kodera T, Oda S, Hoshi Y, Usami N, Itoh K M, Tarucha S 2018 Nat. Nanotechnol. 13 102 Google Scholar
[3]	Huang W, Yang C H, Chan K W, Tanttu T, Hensen B, Leon R C C, Fogarty M A, Hwang J C C, Hudson F E, Itoh K M, Morello A, Laucht A, Dzurak A S 2019 Nature 569 532 Google Scholar
[4]	Yang A, Steger M, Sekiguchi T, Thewalt M L W, Ladd T D, Itoh K M, Riemann H, Abrosimov N V, Becker P, Pohl H J 2009 Phys. Rev. Lett. 102 257401 Google Scholar
[5]	He Y, Gorman S K, Keith D, Kranz L, Keizer J G, Simmons M Y 2019 Nature 571 371 Google Scholar
[6]	Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1 Google Scholar
[7]	Dobrovitski V V, Fuchs G D, Falk A L, Santori C, Awschalom D D 2013 Annu. Rev. Condens. Matter Phys. 4 23 Google Scholar
[8]	Rembold P, Oshnik N, Müller M M, Montangero S, Calarco T, Neu E 2020 AVS Quantum Sci. 2 024701 Google Scholar
[9]	伍旸 2020 博士学位论文 (合肥: 中国科学技术大学) Wu Y 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[10]	Gali A, Fyta M, Kaxiras E 2008 Phys. Rev. B 77 155206 Google Scholar
[11]	Acosta V M, Jarmola A, Bauch E, Budker D 2010 Phys. Rev. B 82 201202 Google Scholar
[12]	Loubser J, van Wyk J 1978 Rep. Prog. Phys. 41 1201 Google Scholar
[13]	Manson N B, Harrison J P, Sellars M J 2006 Phys. Rev. B 74 104303 Google Scholar
[14]	Nizovtsev A P, Kilin S Y, Jelezko F, Popa I, Gruber A, Tietz C, Wrachtrup J 2003 Opt. Spectrosc. 94 848 Google Scholar
[15]	Van der Sar T, Wang Z H, Blok M S, Bernien H, Taminiau T H, Toyli D M, Lidar D A, Awschalom D D, Hanson R, Dobrovitski V V 2012 Nature 484 82 Google Scholar
[16]	Weil J A, Bolton J R 2007 Electron Paramagnetic Resonance: Elementary Theory and Practical Applications (Hoboken: John Wiley & Sons, Inc.)
[17]	Victor A C 1962 J. Chem. Phys. 36 1903 Google Scholar
[18]	Rong X, Geng J P, Shi F Z, Liu Y, Xu K B, Ma W C, Kong F, Jiang Z, Wu Y, Du J F 2015 Nat. Commun. 6 8748 Google Scholar
[19]	De Raedt H, Barbara B, Miyashita S, Michielsen K, Bertaina S, Gambarelli S 2012 Phys. Rev. B 85 014408 Google Scholar
[20]	Rong X, Geng J P, Wang Z X, Zhang Q, Ju C Y, Shi F Z, Duan C K, Du J F 2014 Phys. Rev. Lett. 112 050503 Google Scholar
[21]	Geng J P, Wu Y, Wang X T, Xu K B, Shi F Z, Xie Y J, Rong X, Du J F 2016 Phys. Rev. Lett. 117 170501 Google Scholar
[22]	Wu Y, Wang Y, Qin X, Rong X, Du J F 2019 Npj Quantum Inf. 5 1 Google Scholar
[23]	Wu Y, Liu W Q, Geng J P, Song X R, Ye X Y, Duan C K, Rong X, Du J F 2019 Science 364 878 Google Scholar
[24]	Viola L, Knill E, Lloyd S 1999 Phys. Rev. Lett. 82 2417 Google Scholar
[25]	Khodjasteh K, Lidar D A 2005 Phys. Rev. Lett. 95 180501
[26]	Uhrig G S 2007 Phys. Rev. Lett. 98 100504 Google Scholar
[27]	Du J F, Rong X, Zhao N, Wang Y, Yang J H, Liu R B 2009 Nature 461 1265 Google Scholar
[28]	De Lange G, Wang Z H, Riste D, Dobrovitski V V, Hanson R 2010 Science 330 60 Google Scholar
[29]	Naydenov B, Dolde F, Hall L T, Shin C, Fedder H, Hollenberg L C, Jelezko F, Wrachtrup J 2011 Phys. Rev. B 83 081201 Google Scholar
[30]	Liu G Q, Po H C, Du J, Liu R B, Pan X Y 2013 Nat. Commun. 4 2254
[31]	Zhang J F, Souza A M, Brandao F D, Suter D 2014 Phys. Rev. Lett. 112 050502 Google Scholar
[32]	Khodjasteh K, Viola L 2009 Phys. Rev. Lett. 102 080501 Google Scholar
[33]	Khodjasteh K, Lidar D A, Viola L 2010 Phys. Rev. Lett. 104 090501 Google Scholar
[34]	West J R, Lidar D A, Fong B H, Gyure M F 2010 Phys. Rev. Lett. 105 230503 Google Scholar
[35]	Kestner J P, Wang X, Bishop L S, Barnes E, Das Sarma S 2013 Phys. Rev. Lett. 110 140502
[36]	Wang X, Bishop L S, Kestner J P, Barnes E, Sun K, Dar Sarma S 2012 Nat. Commun. 3 997
[37]	Nielsen M A, Chuang I L 2000 Quantum Computing and Quantum Information (Cambridge: Cambridge University Press)
[38]	Wimperis S 1994 J. Magn. Reson. 109 221 Google Scholar
[39]	Ichikawa T, Bando M, Kondo Y, Nakahara M 2011 Phys. Rev. A 84 062311 Google Scholar
[40]	Bando M, Ichikawa T, Kondo Y, Nakahara M 2013 J. Phys. Soc. Japan 82 014004
[41]	Cummins H K, Llewellyn G, Jones J A 2003 Phys. Rev. A 67 042308 Google Scholar
[42]	Knill E, Leibfried D, Reichle R, Britton J, Blakestad R B, Jost J D, Langer C, Ozeri R, Seidelin S, Wineland D J 2008 Phys. Rev. A 77 012307 Google Scholar
[43]	Fowler A G, Mariantoni M, Martinis J M, Cleland A N 2012 Phys. Rev. A 86 032324 Google Scholar
[44]	Zermelo E 1931 Z. Angew. Math. Mech. 11 114 Google Scholar
[45]	Wang X T, Allegra M, Jacobs K, Lloyd S, Lupo C, Mohseni M 2015 Phys. Rev. Lett. 114 170501 Google Scholar
[46]	Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth B, Neill C, O'Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500 Google Scholar
[47]	Nielsen M A, Chuang I L 1997 Phys. Rev. Lett. 79 321 Google Scholar
[48]	Kim J, Cheong Y, Lee J S, Lee S 2001 Phys. Rev. A 65 012302 Google Scholar
[49]	Vidal G, Masanes L, Cirac J I 2002 Phys. Rev. Lett. 88 047905 Google Scholar
[50]	Shende V V, Markov I L, Bullock S S 2004 Phys. Rev. A 69 062321
[51]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[52]	Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401 Google Scholar
[53]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[54]	Mostafazadeh A 2005 J. Math. Phys. 46 102108 Google Scholar
[55]	Dorey P, Dunning C, Lishman A, Tateo R 2009 J. Phys. A: Math. Theor. 42 465302
[56]	Gong J, Wang Q 2013 J. Phys. A: Math. Theor. 46 485302
[57]	Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808 Google Scholar
[58]	Song F, Yao S Y, Wang Z 2019 Phys. Rev. Lett. 123 170401 Google Scholar
[59]	Gong Z, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M 2018 Phys. Rev. X 8 031079
[60]	Özdemir Ş K, Rotter S, Nori F, Yang L 2019 Nat. Mater. 18 783 Google Scholar
[61]	Miri M-A, Alù A 2019 Science 363 eaar7709
[62]	Bender N, Factor S, Bodyfelt J D, Ramezani H, Christodoulides D N, Ellis F M, Kottos T 2013 Phys. Rev. Lett. 110 234101 Google Scholar
[63]	Assawaworrarit S, Yu X, Fan S 2017 Nature 546 387 Google Scholar
[64]	Choi Y, Hahn C, Yoon J W, Song S H 2018 Nat. Commun. 9 2182
[65]	Bittner S, Dietz B, Günther U, Harney H L, Miski-Oglu M, Richter A, Schäfer F 2012 Phys. Rev. Lett. 108 024101 Google Scholar
[66]	Bender C M, Berntson B K, Parker D, Samuel E 2013 Am. J. Phys. 81 173 Google Scholar
[67]	Zhu X F, Ramezani H, Shi C Z, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
[68]	Popa B I, Cummer S A 2014 Nat. Commun. 5 3398
[69]	Fleury R, Sounas D, Alù A 2015 Nat. Commun. 6 5905
[70]	Li J M, Harter A K, Liu J, de Melo L, Joglekar Y N, Luo L 2019 Nat. Commun. 10 855
[71]	Naghiloo M, Abbasi M, Joglekar Y N, Murch K W 2019 Nat. Phys. 15 1232 Google Scholar
[72]	Liu W Q, Wu Y, Duan C K, Rong X, Du J F 2021 Phys. Rev. Lett. 126 170506 Google Scholar
[73]	Lau H K, Clerk A A 2018 Nat. Commun. 9 4320
[74]	Chen C, Jin L, Liu R B 2019 New J. Phys. 21 083002 Google Scholar

施引文献

图 1 金刚石中NV色心结构图^[9]

Fig. 1. Schematic atomic structure of the NV center in diamond^[9].

下载: 全尺寸图片幻灯片

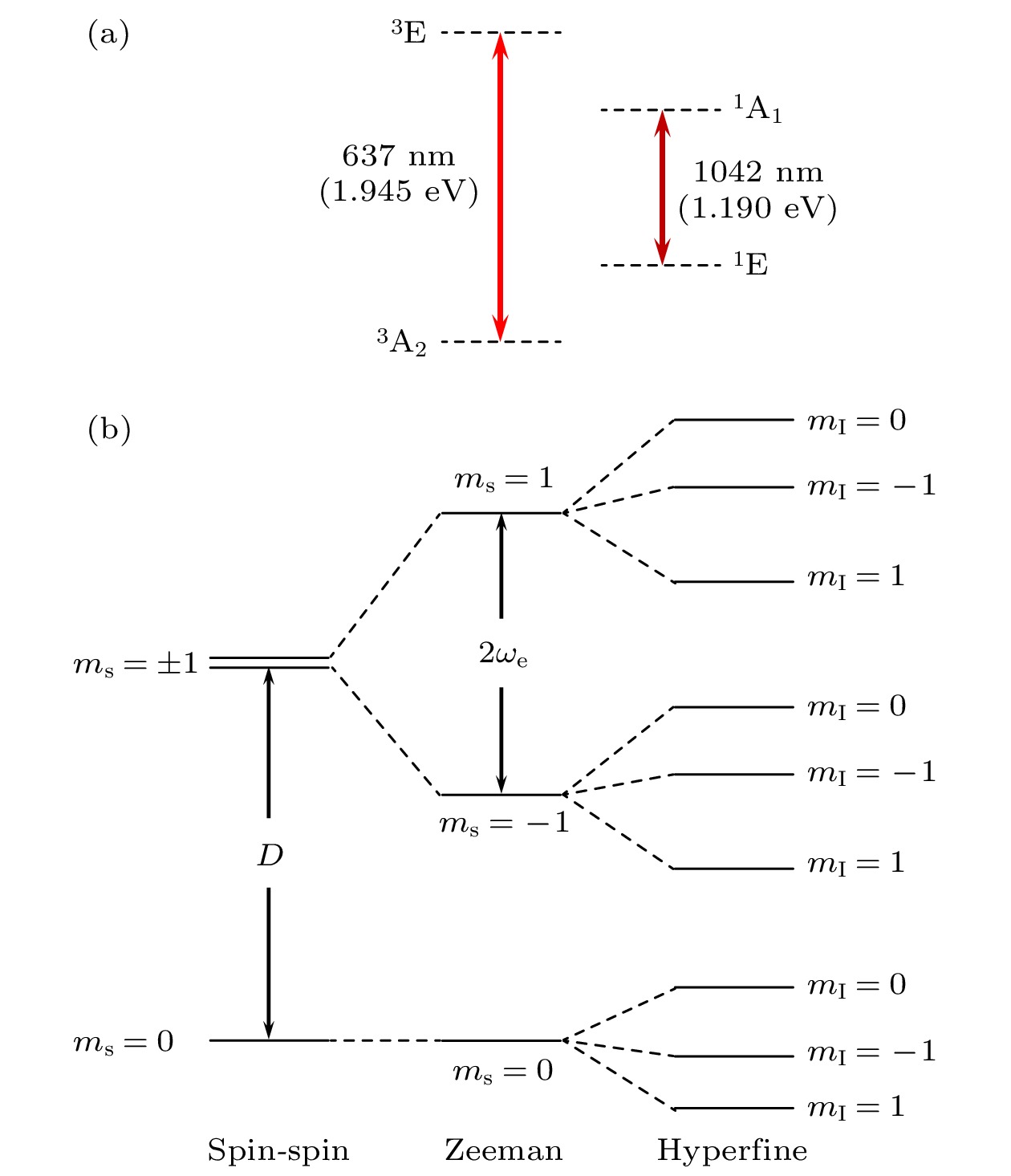
图 2 金刚石NV色心能级结构^[9]　(a) NV色心的基态、激发态和亚稳态; (b) NV色心基态的精细结构和¹⁴N核带来的超精细结构

Fig. 2. Energy level diagram of the NV center in diamond^[9]: (a) Ground state, excited state and metastable state of the NV center; (b) fine structure and hyperfine structure (caused by ¹⁴N nuclear spin) of the NV center ground state.

下载: 全尺寸图片幻灯片

图 3 NV色心电子自旋的退相位过程^[18]　(a) 电子自旋的自由感应衰减曲线, 插图为实验脉冲序列; (b) 准静态噪声$ \delta_0 $的分布$ P(\delta_0 $)

Fig. 3. Dephasing process of the electron spin of the NV center^[18]: (a) FID of the electron spin, the inset is the experimental pulse sequence; (b) probability density distribution of $ \delta_0 $.

下载: 全尺寸图片幻灯片

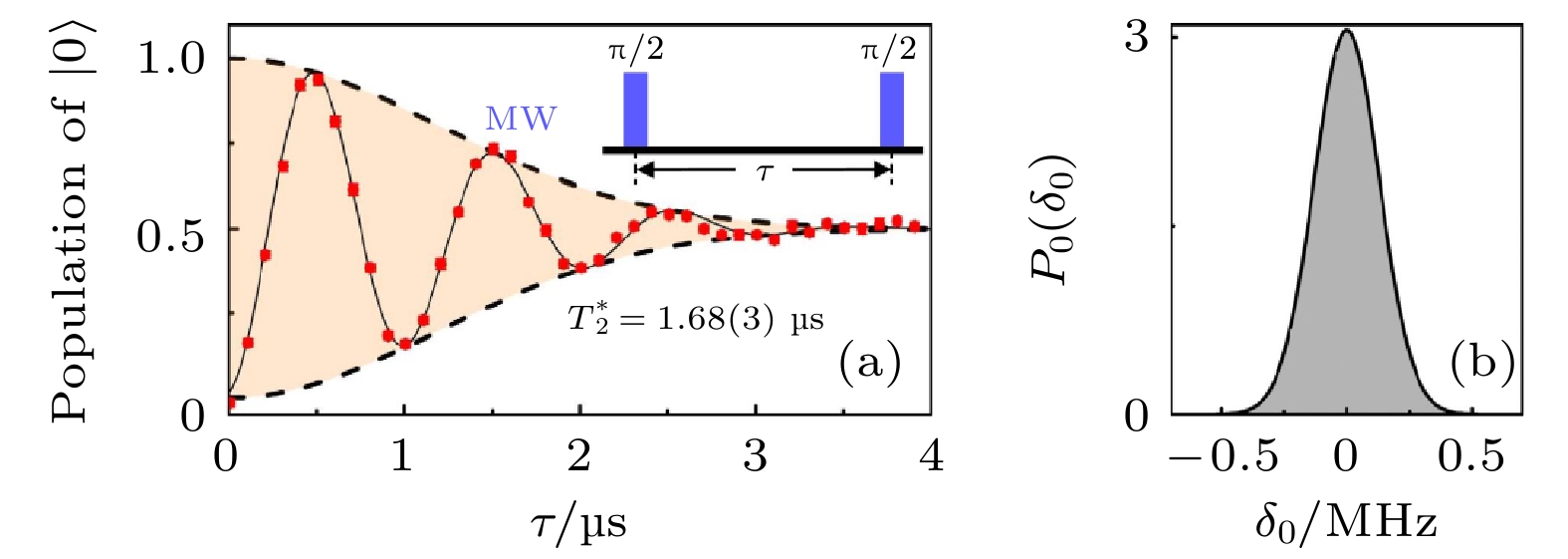
图 4 操控场噪声下NV色心的退相干^[18]　(a) 电子自旋的拉比振荡, 插图为实验脉冲序列; (b) 准静态操控场噪声$ \delta_1 $的分布$ P(\delta_1 $)

Fig. 4. Decoherence of the NV center under control field noise^[18]: (a) Results of the nutation experiment for the electron spin, the inset is the experimental pulse sequence; (b) probability density distribution of $ \delta_1 $.

下载: 全尺寸图片幻灯片

图 5 实验验证SUPCODE序列在实现量子逻辑门时对准静态环境噪声的抑制效果^[20]

Fig. 5. Experimental demonstration of the robustness of SUPCODE against the noise stemming from the quasistatic fluctuation of Overhauser field^[20].

下载: 全尺寸图片幻灯片

图 6 级联5-piece SUPCODE序列实现的量子逻辑门保真度随序列时长的关系^[20]

Fig. 6. Decay of the fidelity of 5-piece SUPCODEs^[20].

下载: 全尺寸图片幻灯片

图 7 实现量子逻辑门的各种脉冲序列及在噪声影响下的保真度^[18]　(a) 普通方波脉冲; (b) 5-piece SUPCODE脉冲序列; (c) BB1脉冲序列; (d) BB1inC脉冲序列

Fig. 7. Pulse sequences for quantum gate and the fidelity under noises^[18]: (a) Plain pulse; (b) 5-piece SUPCODE pulse; (c) BB1 pulse; (d) BB1inC pulse.

下载: 全尺寸图片幻灯片

图 8 单比特量子逻辑门保真度的实验测量结果, 插图为四种脉冲序列对应的量子逻辑门的出错概率$ \varepsilon $^[18]

Fig. 8. Average fidelity of single-qubit gates, where the inset shows the average error per gates of the pulses^[18].

下载: 全尺寸图片幻灯片

图 9 测量CNOT门保真度的量子线路图(a)和实验结果(b)^[18]

Fig. 9. Quantum circuit diagram (a) and experimental result (b) for measuring the fidelity of CNOT gates^[18].

下载: 全尺寸图片幻灯片

图 10 时间最优控制示意图^[21]

Fig. 10. Schematic diagram of time optimal quantum control^[21].

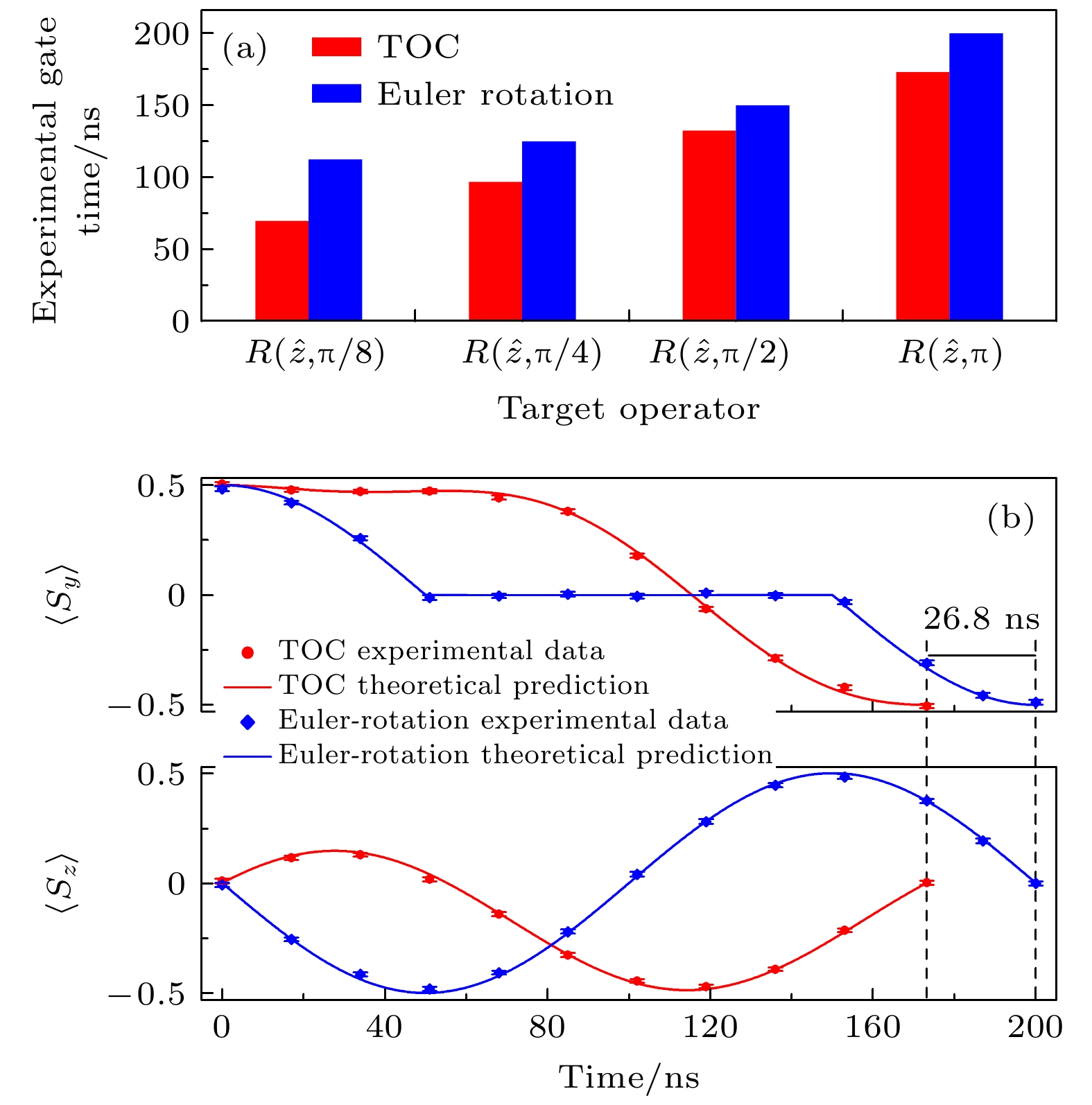
下载: 全尺寸图片幻灯片

图 11 时间最优量子控制和欧拉转动实现单比特操控$ R(\hat{z}, \theta) $花费时间对比^[21]　(a) 转角$ \theta $分别为$ \pi/8 $, $ \pi/4 $, $ \pi/2 $和$ \pi $时, 实现单比特操控$ R(\hat{z}, \theta) $耗时对比; (b) 时间最优量子控制和欧拉转动下量子态的演化过程

Fig. 11. Comparison on time costs for target gate operator $ R(\hat{z}, \theta) $ between the derived time-optimal control (TOC) and the Euler rotations^[21]: (a) Comparison of experimental gate time for $ \theta = \pi/8 $, $ \pi/4 $, $ \pi/2 $, and $ \pi $; (b) state evolutions during $ R(\hat{z}, \theta) $ with TOC and Euler rotation.

下载: 全尺寸图片幻灯片

图 12 初态为(a) $ |0, 1\rangle $和 (b) $ |0, 0\rangle $时量子态在两比特时间最优控制下的演化^[21]

Fig. 12. State trajectories under the two-qubit controlled-U gate by TOC with initial states (a) $ |0, 1\rangle $ and (b) $ |0, 0\rangle $^[21].

下载: 全尺寸图片幻灯片

图 13 普适可编程量子逻辑线路^[22]

Fig. 13. Universal programmable quantum logic circuit^[22].

下载: 全尺寸图片幻灯片

图 14 单比特门对应的脉冲^[22]

Fig. 14. Realization of the single-qubit gate^[22].

下载: 全尺寸图片幻灯片

图 15 金刚石NV色心体系中实现PT对称哈密顿量的量子线路图^[23]

Fig. 15. Quantum circuit of the experiment of constructing a PT symmetric Hamiltonian in a NV center^[23].

下载: 全尺寸图片幻灯片

图 16 量子态在PT对称哈密顿量$ H_{PT} $下的演化^[23]　(a) $ r $ = 0, 厄米哈密顿量; (b) $ r $ = 0.6, PT对称非破缺; (c) $ r $ = 1.0, 奇异点; (d) $ r $ = 1.4, PT对称破缺时的情况

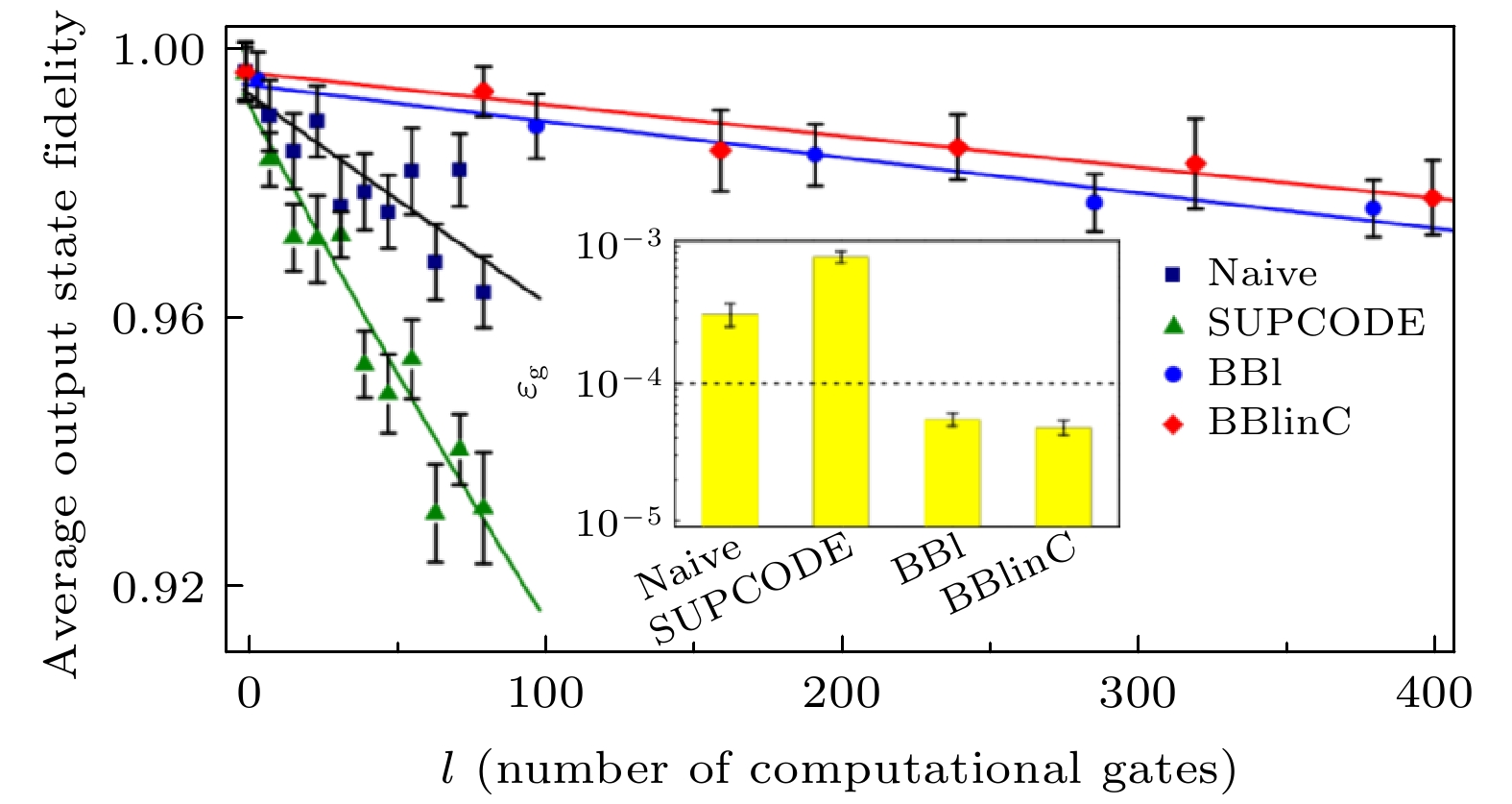
Fig. 16. State evolution under $ H_{PT} $^[23]. Experimental dynamics of renormalized population $ P_0 $ when $ r $ = 0 (a), $ r $ = 0.6 (b), $ r $ = 1.0 (c), and $ r $ = 1.4 (d).

下载: 全尺寸图片幻灯片

表 1 不同量子逻辑门序列下末态保真度的偏差随${\delta_0}/{\omega_1}$的阶数关系^[20]

Table 1. Infidelity of quantum gate for different pulses as a function of ${\delta_0}/{\omega_1}$^[20].

脉冲序列	末态保真度偏差
普通方波脉冲	$0.5(\delta_0/\omega_1)^2+O(\delta_0/\omega_1)^4$
3-piece SUPCODE脉冲	$11.1(\delta_0/\omega_1)^4+O(\delta_0/\omega_1)^6$
5-piece SUPCODE脉冲	$64.1(\delta_0/\omega_1)^6+O(\delta_0/\omega_1)^8$

下载: 导出CSV

map

[1]	Kastner M A 1992 Rev. Mod. Phys. 64 849 Google Scholar
[2]	Yoneda J, Takeda K, Otsuka T, Nakajima T, Delbecq M R, Allison G, Honda T, Kodera T, Oda S, Hoshi Y, Usami N, Itoh K M, Tarucha S 2018 Nat. Nanotechnol. 13 102 Google Scholar
[3]	Huang W, Yang C H, Chan K W, Tanttu T, Hensen B, Leon R C C, Fogarty M A, Hwang J C C, Hudson F E, Itoh K M, Morello A, Laucht A, Dzurak A S 2019 Nature 569 532 Google Scholar
[4]	Yang A, Steger M, Sekiguchi T, Thewalt M L W, Ladd T D, Itoh K M, Riemann H, Abrosimov N V, Becker P, Pohl H J 2009 Phys. Rev. Lett. 102 257401 Google Scholar
[5]	He Y, Gorman S K, Keith D, Kranz L, Keizer J G, Simmons M Y 2019 Nature 571 371 Google Scholar
[6]	Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1 Google Scholar
[7]	Dobrovitski V V, Fuchs G D, Falk A L, Santori C, Awschalom D D 2013 Annu. Rev. Condens. Matter Phys. 4 23 Google Scholar
[8]	Rembold P, Oshnik N, Müller M M, Montangero S, Calarco T, Neu E 2020 AVS Quantum Sci. 2 024701 Google Scholar
[9]	伍旸 2020 博士学位论文 (合肥: 中国科学技术大学) Wu Y 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[10]	Gali A, Fyta M, Kaxiras E 2008 Phys. Rev. B 77 155206 Google Scholar
[11]	Acosta V M, Jarmola A, Bauch E, Budker D 2010 Phys. Rev. B 82 201202 Google Scholar
[12]	Loubser J, van Wyk J 1978 Rep. Prog. Phys. 41 1201 Google Scholar
[13]	Manson N B, Harrison J P, Sellars M J 2006 Phys. Rev. B 74 104303 Google Scholar
[14]	Nizovtsev A P, Kilin S Y, Jelezko F, Popa I, Gruber A, Tietz C, Wrachtrup J 2003 Opt. Spectrosc. 94 848 Google Scholar
[15]	Van der Sar T, Wang Z H, Blok M S, Bernien H, Taminiau T H, Toyli D M, Lidar D A, Awschalom D D, Hanson R, Dobrovitski V V 2012 Nature 484 82 Google Scholar
[16]	Weil J A, Bolton J R 2007 Electron Paramagnetic Resonance: Elementary Theory and Practical Applications (Hoboken: John Wiley & Sons, Inc.)
[17]	Victor A C 1962 J. Chem. Phys. 36 1903 Google Scholar
[18]	Rong X, Geng J P, Shi F Z, Liu Y, Xu K B, Ma W C, Kong F, Jiang Z, Wu Y, Du J F 2015 Nat. Commun. 6 8748 Google Scholar
[19]	De Raedt H, Barbara B, Miyashita S, Michielsen K, Bertaina S, Gambarelli S 2012 Phys. Rev. B 85 014408 Google Scholar
[20]	Rong X, Geng J P, Wang Z X, Zhang Q, Ju C Y, Shi F Z, Duan C K, Du J F 2014 Phys. Rev. Lett. 112 050503 Google Scholar
[21]	Geng J P, Wu Y, Wang X T, Xu K B, Shi F Z, Xie Y J, Rong X, Du J F 2016 Phys. Rev. Lett. 117 170501 Google Scholar
[22]	Wu Y, Wang Y, Qin X, Rong X, Du J F 2019 Npj Quantum Inf. 5 1 Google Scholar
[23]	Wu Y, Liu W Q, Geng J P, Song X R, Ye X Y, Duan C K, Rong X, Du J F 2019 Science 364 878 Google Scholar
[24]	Viola L, Knill E, Lloyd S 1999 Phys. Rev. Lett. 82 2417 Google Scholar
[25]	Khodjasteh K, Lidar D A 2005 Phys. Rev. Lett. 95 180501
[26]	Uhrig G S 2007 Phys. Rev. Lett. 98 100504 Google Scholar
[27]	Du J F, Rong X, Zhao N, Wang Y, Yang J H, Liu R B 2009 Nature 461 1265 Google Scholar
[28]	De Lange G, Wang Z H, Riste D, Dobrovitski V V, Hanson R 2010 Science 330 60 Google Scholar
[29]	Naydenov B, Dolde F, Hall L T, Shin C, Fedder H, Hollenberg L C, Jelezko F, Wrachtrup J 2011 Phys. Rev. B 83 081201 Google Scholar
[30]	Liu G Q, Po H C, Du J, Liu R B, Pan X Y 2013 Nat. Commun. 4 2254
[31]	Zhang J F, Souza A M, Brandao F D, Suter D 2014 Phys. Rev. Lett. 112 050502 Google Scholar
[32]	Khodjasteh K, Viola L 2009 Phys. Rev. Lett. 102 080501 Google Scholar
[33]	Khodjasteh K, Lidar D A, Viola L 2010 Phys. Rev. Lett. 104 090501 Google Scholar
[34]	West J R, Lidar D A, Fong B H, Gyure M F 2010 Phys. Rev. Lett. 105 230503 Google Scholar
[35]	Kestner J P, Wang X, Bishop L S, Barnes E, Das Sarma S 2013 Phys. Rev. Lett. 110 140502
[36]	Wang X, Bishop L S, Kestner J P, Barnes E, Sun K, Dar Sarma S 2012 Nat. Commun. 3 997
[37]	Nielsen M A, Chuang I L 2000 Quantum Computing and Quantum Information (Cambridge: Cambridge University Press)
[38]	Wimperis S 1994 J. Magn. Reson. 109 221 Google Scholar
[39]	Ichikawa T, Bando M, Kondo Y, Nakahara M 2011 Phys. Rev. A 84 062311 Google Scholar
[40]	Bando M, Ichikawa T, Kondo Y, Nakahara M 2013 J. Phys. Soc. Japan 82 014004
[41]	Cummins H K, Llewellyn G, Jones J A 2003 Phys. Rev. A 67 042308 Google Scholar
[42]	Knill E, Leibfried D, Reichle R, Britton J, Blakestad R B, Jost J D, Langer C, Ozeri R, Seidelin S, Wineland D J 2008 Phys. Rev. A 77 012307 Google Scholar
[43]	Fowler A G, Mariantoni M, Martinis J M, Cleland A N 2012 Phys. Rev. A 86 032324 Google Scholar
[44]	Zermelo E 1931 Z. Angew. Math. Mech. 11 114 Google Scholar
[45]	Wang X T, Allegra M, Jacobs K, Lloyd S, Lupo C, Mohseni M 2015 Phys. Rev. Lett. 114 170501 Google Scholar
[46]	Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth B, Neill C, O'Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500 Google Scholar
[47]	Nielsen M A, Chuang I L 1997 Phys. Rev. Lett. 79 321 Google Scholar
[48]	Kim J, Cheong Y, Lee J S, Lee S 2001 Phys. Rev. A 65 012302 Google Scholar
[49]	Vidal G, Masanes L, Cirac J I 2002 Phys. Rev. Lett. 88 047905 Google Scholar
[50]	Shende V V, Markov I L, Bullock S S 2004 Phys. Rev. A 69 062321
[51]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[52]	Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401 Google Scholar
[53]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[54]	Mostafazadeh A 2005 J. Math. Phys. 46 102108 Google Scholar
[55]	Dorey P, Dunning C, Lishman A, Tateo R 2009 J. Phys. A: Math. Theor. 42 465302
[56]	Gong J, Wang Q 2013 J. Phys. A: Math. Theor. 46 485302
[57]	Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808 Google Scholar
[58]	Song F, Yao S Y, Wang Z 2019 Phys. Rev. Lett. 123 170401 Google Scholar
[59]	Gong Z, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M 2018 Phys. Rev. X 8 031079
[60]	Özdemir Ş K, Rotter S, Nori F, Yang L 2019 Nat. Mater. 18 783 Google Scholar
[61]	Miri M-A, Alù A 2019 Science 363 eaar7709
[62]	Bender N, Factor S, Bodyfelt J D, Ramezani H, Christodoulides D N, Ellis F M, Kottos T 2013 Phys. Rev. Lett. 110 234101 Google Scholar
[63]	Assawaworrarit S, Yu X, Fan S 2017 Nature 546 387 Google Scholar
[64]	Choi Y, Hahn C, Yoon J W, Song S H 2018 Nat. Commun. 9 2182
[65]	Bittner S, Dietz B, Günther U, Harney H L, Miski-Oglu M, Richter A, Schäfer F 2012 Phys. Rev. Lett. 108 024101 Google Scholar
[66]	Bender C M, Berntson B K, Parker D, Samuel E 2013 Am. J. Phys. 81 173 Google Scholar
[67]	Zhu X F, Ramezani H, Shi C Z, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
[68]	Popa B I, Cummer S A 2014 Nat. Commun. 5 3398
[69]	Fleury R, Sounas D, Alù A 2015 Nat. Commun. 6 5905
[70]	Li J M, Harter A K, Liu J, de Melo L, Joglekar Y N, Luo L 2019 Nat. Commun. 10 855
[71]	Naghiloo M, Abbasi M, Joglekar Y N, Murch K W 2019 Nat. Phys. 15 1232 Google Scholar
[72]	Liu W Q, Wu Y, Duan C K, Rong X, Du J F 2021 Phys. Rev. Lett. 126 170506 Google Scholar
[73]	Lau H K, Clerk A A 2018 Nat. Commun. 9 4320
[74]	Chen C, Jin L, Liu R B 2019 New J. Phys. 21 083002 Google Scholar

[1]	王粲, 陆朝阳, 陈明城. 时间旅行的量子门. , 2024, 73(2): 020303. doi: 10.7498/aps.73.20231289
[2]	何健, 贾燕伟, 屠菊萍, 夏天, 朱肖华, 黄珂, 安康, 刘金龙, 陈良贤, 魏俊俊, 李成明. 碳离子注入金刚石制备氮空位色心的机理. , 2022, 71(18): 188102. doi: 10.7498/aps.71.20220794
[3]	林豪彬, 张少春, 董杨, 郑瑜, 陈向东, 孙方稳. 基于金刚石氮-空位色心的温度传感. , 2022, 71(6): 060302. doi: 10.7498/aps.71.20211822
[4]	吴建冬, 程智, 叶翔宇, 李兆凯, 王鹏飞, 田长麟, 陈宏伟. 金刚石氮-空位色心单电子自旋的电场驱动相干控制研究. , 2022, 0(0): . doi: 10.7498/aps.71.20220410
[5]	吴建冬, 程智, 叶翔宇, 李兆凯, 王鹏飞, 田长麟, 陈宏伟. 金刚石氮-空位色心单电子自旋的电场驱动相干控制. , 2022, 71(11): 117601. doi: 10.7498/aps.70.20220410
[6]	刘腾, 陆鹏飞, 胡碧莹, 吴昊, 劳祺峰, 边纪, 刘泱, 朱峰, 罗乐. 离子阱中以声子为媒介的多体量子纠缠与逻辑门. , 2022, 71(8): 080301. doi: 10.7498/aps.71.20220360
[7]	沈翔, 赵立业, 黄璞, 孔熙, 季鲁敏. 金刚石氮-空位色心的原子自旋声子耦合机理. , 2021, 70(6): 068501. doi: 10.7498/aps.70.20201848
[8]	金钊, 李芮, 公卫江, 祁阳, 张寿, 苏石磊. 基于共振里德伯偶极-偶极相互作用的双反阻塞机制及量子逻辑门的实现. , 2021, 70(13): 134202. doi: 10.7498/aps.70.20210059
[9]	冯园耀, 李中豪, 张扬, 崔凌霄, 郭琦, 郭浩, 温焕飞, 刘文耀, 唐军, 刘俊. 固态金刚石氮空位色心光学调控优化. , 2020, 69(14): 147601. doi: 10.7498/aps.69.20200072
[10]	张茜, 李萌, 龚旗煌, 李焱. 飞秒激光直写光量子逻辑门. , 2019, 68(10): 104205. doi: 10.7498/aps.68.20190024
[11]	廖庆洪, 叶杨, 李红珍, 周南润. 金刚石氮空位色心耦合机械振子和腔场系统中方差压缩研究. , 2018, 67(4): 040302. doi: 10.7498/aps.67.20172170
[12]	彭世杰, 刘颖, 马文超, 石发展, 杜江峰. 基于金刚石氮-空位色心的精密磁测量. , 2018, 67(16): 167601. doi: 10.7498/aps.67.20181084
[13]	刘刚钦, 邢健, 潘新宇. 金刚石氮空位中心自旋量子调控. , 2018, 67(12): 120302. doi: 10.7498/aps.67.20180755
[14]	董杨, 杜博, 张少春, 陈向东, 孙方稳. 基于金刚石体系中氮-空位色心的固态量子传感. , 2018, 67(16): 160301. doi: 10.7498/aps.67.20180788
[15]	李雪琴, 赵云芳, 唐艳妮, 杨卫军. 基于金刚石氮-空位色心自旋系综与超导量子电路混合系统的量子节点纠缠. , 2018, 67(7): 070302. doi: 10.7498/aps.67.20172634
[16]	李路思, 李红蕙, 周黎黎, 杨炙盛, 艾清. 利用金刚石氮-空位色心精确测量弱磁场的探索. , 2017, 66(23): 230601. doi: 10.7498/aps.66.230601
[17]	李俊, 崔江煜, 杨晓东, 罗智煌, 潘健, 余琦, 李兆凯, 彭新华, 杜江峰. 核磁共振中的量子控制. , 2015, 64(16): 167601. doi: 10.7498/aps.64.167601
[18]	刘东奇, 常彦春, 刘刚钦, 潘新宇. 金刚石纳米颗粒中氮空位色心的电子自旋研究. , 2013, 62(16): 164208. doi: 10.7498/aps.62.164208
[19]	李永放, 任立庆, 马瑞琼, 樊荣, 刘娟. 利用相位可控光场实现量子态波函数时域演化的量子控制. , 2010, 59(3): 1671-1676. doi: 10.7498/aps.59.1671
[20]	李艳玲, 冯健. 利用单个三粒子最大GHZ态或两个EPR态隐形传送任意三粒子GHZ态. , 2007, 56(4): 1888-1894. doi: 10.7498/aps.56.1888

计量

文章访问数: 6833
PDF下载量: 394
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板