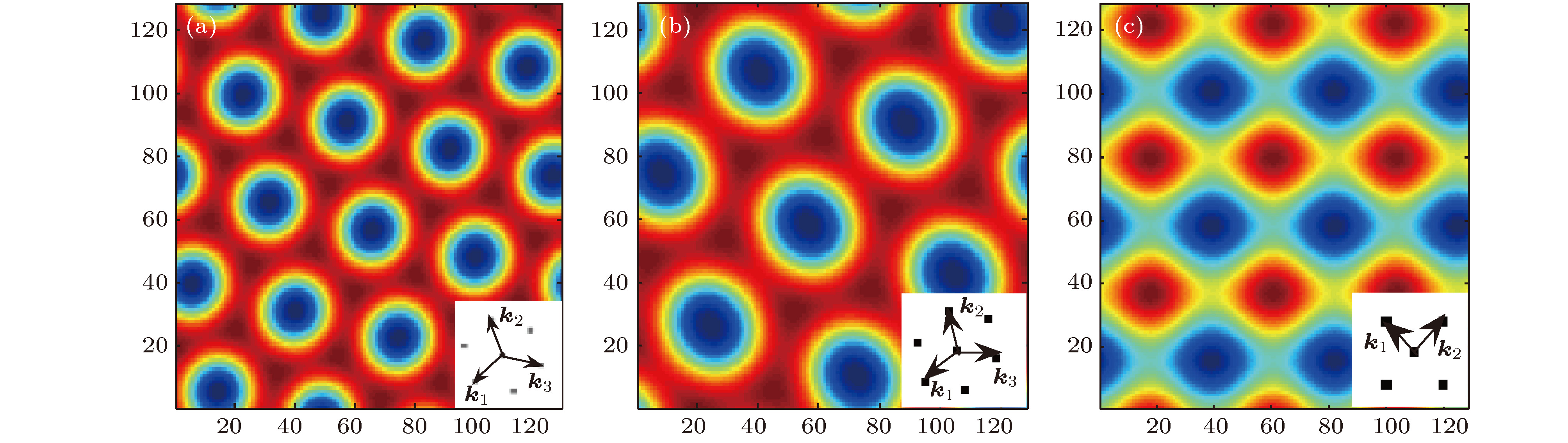
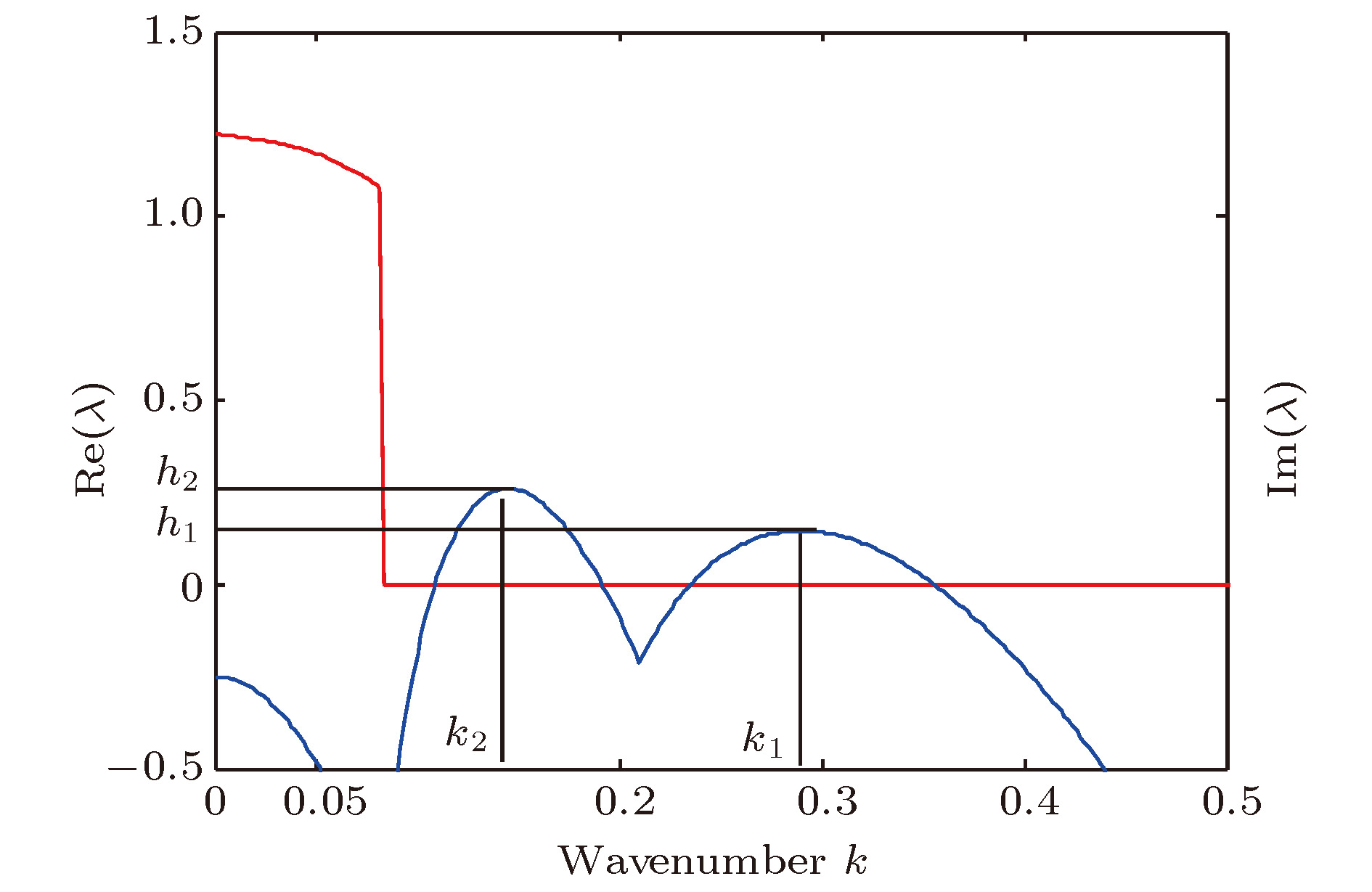
-
In this paper, the simple and superlattice square patterns in two-dimensional space are investigated numerically by the two-layer coupled Lengyel-Epstein model. When the wave number ratio of Turing modes is greater than one, our results show that the spatial resonance form of the fundamental mode is changed with the increase of coupling strength, and simple hexagon pattern evolves spontaneously into a new pattern with a complicated structure. In addition to the reported superlattice hexagonal pattern, simple square pattern and superlattice square pattern are obtained, such as the complicated big-small spot, spot-line, ring and white-eye square pattern. The characteristics of simple and complicated superlattice square pattern are investigated by the intermediate process of evolution. When the coupling parameters
$\alpha $ and$\beta $ increase synchronously within a certain range, the type I square patterns of the same wavelength are obtained in the two subsystems. When the coupling parameters$\alpha $ and$\beta $ increase asynchronously, the type I square pattern can evolve into the type II square pattern on the same spatial scale through phase transition. Then, the new subharmonic modes are generated, and the complicated superlattice square patterns are obtained due to the resonance between the two Turing modes in a short wavelength mode subsystem. The influence of coupling between two subsystems on the square pattern is investigated. When the type I square pattern of wavelength$\lambda $ emerges, the square pattern will quickly lose its stability in the short wavelength mode subsystem, since the coupling coefficient is equal to zero. Finally a new square pattern of wavelength$\lambda $ /N is formed. The type I square patterns of two subsystems successively evolve into the type II square patterns through the phase transition. The spots move relatively with the extension of simulation time, and a new mode is generated and forms three-wave resonance in two subsystems, and then the hexagonal pattern dominates the system. Our results also show that the type II square pattern spontaneously transforms into a hexagonal pattern.[1] Landry W, Werner B T 1994 Physica D 77 238
Google Scholar
[2] Zhou C X, Guo H Y, Ouyang Q 2002 Phys. Rev. E 65 036118
Google Scholar
[3] Pampaloni E, Residori S, Soria S, Arecchi F T 1997 Phys. Rev. Lett. 78 1042
Google Scholar
[4] Cysyk J, Tung L 2008 Biophys. J. 94 1533
Google Scholar
[5] 刘海英, 杨翠云, 唐国宁 2013 62 010505
Google Scholar
Liu H Y, Yang C Y, Tang G N 2013 Acta Phys. Sin. 62 010505
Google Scholar
[6] Le Gal P, Pocheau A, Croquette V 1985 Phys. Rev. Lett. 54 2501
Google Scholar
[7] Wagner C, Müller H W, Knorr K 2000 Phys. Rev. E 62 33
Google Scholar
[8] Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2006 Chaos 16 037114
Google Scholar
[9] Dong L F, Fan W L, He Y F, Liu F C, Li S F, Gao R L, Wang L 2006 Phys. Rev. E 73 066206
Google Scholar
[10] Wei L Y, Dong L F, Feng J Y, Liu W B, Fan W L, Pan Y Y 2016 J. Phys. D: Appl. Phys. 49 185203
Google Scholar
[11] Pagea K M, Maini P K, Monk N A M 2005 Physica D 202 95
Google Scholar
[12] Yang L F, Zhabotinsky A M, Epstein I R 2004 Phys. Rev. Lett. 92 198303
Google Scholar
[13] Li J, Wang H L, Ouyang Q 2014 Chaos 24 023115
Google Scholar
[14] Judd S L, Silber M 2000 Physica D 136 45
Google Scholar
[15] Turing A M 1952 Philos. Trans. R. Soc. London, Ser. B 237 37
Google Scholar
[16] Qian Y, Gao H Y, Yao C G, Cui X H, Ma J 2018 Chin. Phys. B 27 108902
Google Scholar
[17] Mikhailova A S, Showalter K 2006 Phys. Rep. 425 79
Google Scholar
[18] 张荣培, 王震, 王语, 韩子健 2018 67 050503
Google Scholar
Zhang R P, Wang Z, Wang Y, Han Z J 2018 Acta Phys. Sin. 67 050503
Google Scholar
[19] Zhang L S, Liao X H, Mi Y Y, Qian Y, Hu G 2014 Chin. Phys. B 23 078906
Google Scholar
[20] Míguez D G, Dolnik M, Epstein I R, Muñuzuri A P 2011 Phys. Rev. E 84 046210
Google Scholar
[21] Gambino G, Lombardo M C, Sammartino M 2014 Acta Appl. Math. 132 283
Google Scholar
[22] Dong L F, He Y F, Liu W L, Gao R L, Wang H F, Zhao H T 2007 Appl. Phys. Lett. 90 031504
Google Scholar
[23] Barrio R A, Varea C, Aragon J L, Maini P K 1999 Bull. Math. Biol. 61 483
Google Scholar
[24] Dong L F, Fan W L, Pan Y Y 2010 Plasma Sci. Technol. 12 172
Google Scholar
-
图 1 两子系统图灵模型的色散曲线
Figure 1. Dispersion curves of Turing mode in two subsystems.
图 2 无耦合时两子系统生成的六边形(a), (b)及耦合时生成的正四边形(c)
Figure 2. Hexagonal patterns (a), (b) without coupling and square pattern (c) with coupling in the two subsystems.
图 3 失去耦合后两子系统中正四边斑图的自发演化
Figure 3. Spontaneous evolution of square patterns in two subsystems after loss of coupling.
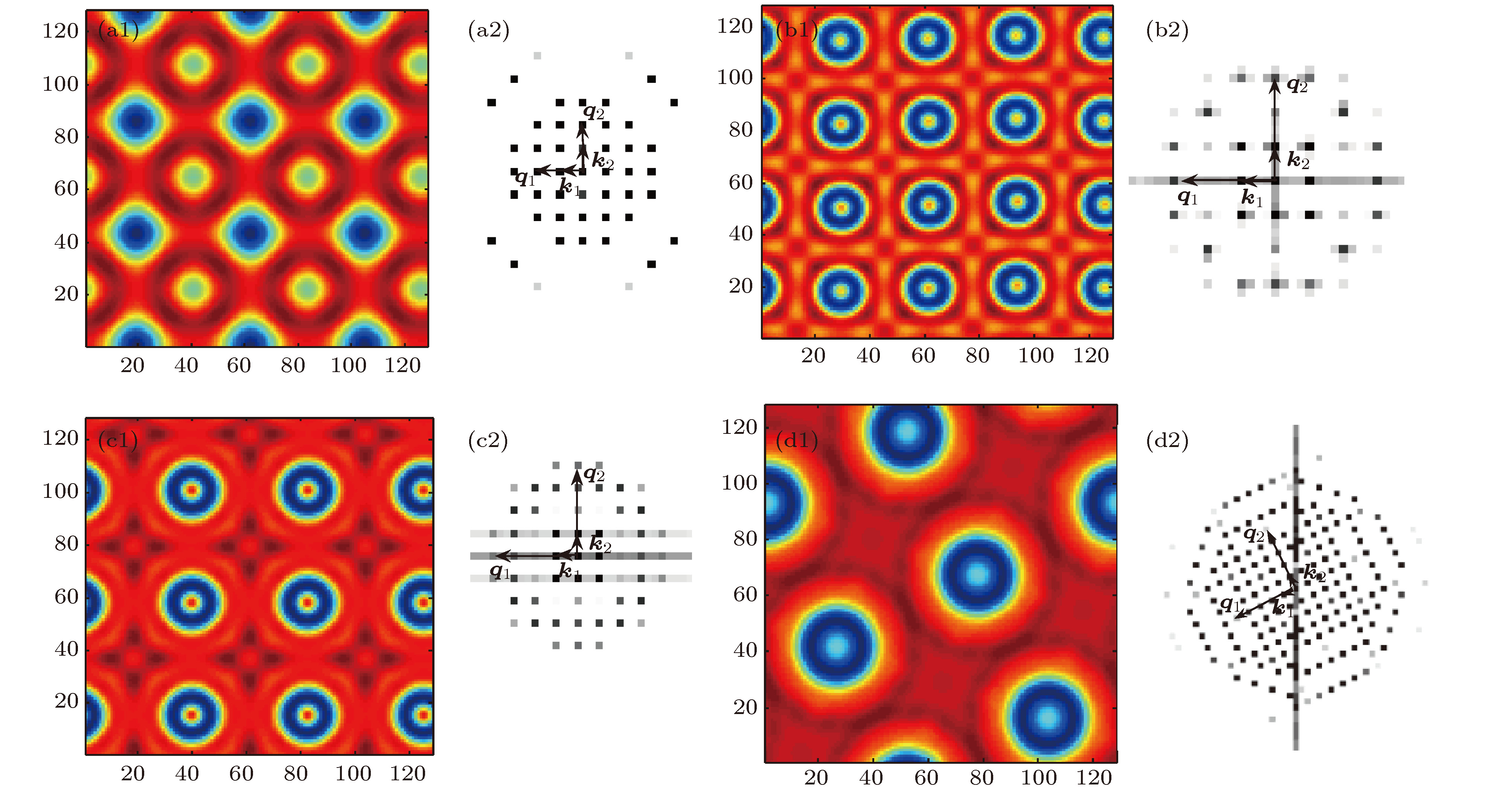
图 4 (a)—(f)大小点超四边的形成过程, 模拟时间顺序为463.8, 827.9, 893.2, 927.8, 957.4, 975.0; (g) 空间傅里叶频谱; (h) 波形空间分布(
$\alpha = 0.085$ ,$\beta = 0.11$ , 其余参数见图2)Figure 4. (a)−(f) Formation process of big-small spot square pattern, and the simulation time sequence is as follows: 463.8, 827.9, 893.2, 927.8, 957.4, and 975.0; (g) Fourier spectrum; (h) waveform diagram (
$\alpha = 0.085$ ,$\beta = 0.11$ , the other parameters is the same value of Fig. 2).
图 5 不同波数比时系统形成的超四边形 (a)复杂大小点四边, Du1 = 11.885, Dv1 = 163.425, Du2 = 46.30, Dv2 = 671.25,
$\alpha = 0.075$ ,$\beta = 0.11$ ; (b) 点线四边, Du1 = 2.95, Dv1 = 41.15, Du2 = 25.75, Dv2 = 382.05,$\alpha = 0.085$ ,$\beta = 0.11$ ; (c)环状四边, Du1 = 2.95, Dv1 = 41.15, Du2 = 45.90, Dv2 = 677.05,$\alpha = 0.085$ ,$\beta = 0.11$ ; (d)白眼四边, Du1 = 2.95, Dv1 = 41.15, Du2 = 71.0, Dv2 = 1065.25,$\alpha = 0.075$ ,$\beta = 0.11$ Figure 5. Square superlattice pattern at different wavenumber ratios: (a) Complex big-small spot square pattern, Du1 = 11.885, Dv1 = 163.425, Du2 = 46.30, Dv2 = 671.25,
$\alpha = 0.075$ ,$\beta = 0.11$ ; (b) spot-line square pattern, Du1 = 2.95, Dv1 = 41.15, Du2 = 25.75, Dv2 = 382.05,$\alpha = 0.085$ ,$\beta = 0.11$ ; (c) ring square pattern, Du1 = 2.95, Dv1 = 41.15, Du2 = 45.90, Dv2 = 677.05,$\alpha = 0.085$ ,$\beta = 0.11$ ; (d) white-eye square pattern, Du1 = 2.95, Dv1 = 41.15, Du2 = 71.0, Dv2 = 1065.25,$\alpha = 0.075$ ,$\beta = 0.11$ . -
[1] Landry W, Werner B T 1994 Physica D 77 238
Google Scholar
[2] Zhou C X, Guo H Y, Ouyang Q 2002 Phys. Rev. E 65 036118
Google Scholar
[3] Pampaloni E, Residori S, Soria S, Arecchi F T 1997 Phys. Rev. Lett. 78 1042
Google Scholar
[4] Cysyk J, Tung L 2008 Biophys. J. 94 1533
Google Scholar
[5] 刘海英, 杨翠云, 唐国宁 2013 62 010505
Google Scholar
Liu H Y, Yang C Y, Tang G N 2013 Acta Phys. Sin. 62 010505
Google Scholar
[6] Le Gal P, Pocheau A, Croquette V 1985 Phys. Rev. Lett. 54 2501
Google Scholar
[7] Wagner C, Müller H W, Knorr K 2000 Phys. Rev. E 62 33
Google Scholar
[8] Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2006 Chaos 16 037114
Google Scholar
[9] Dong L F, Fan W L, He Y F, Liu F C, Li S F, Gao R L, Wang L 2006 Phys. Rev. E 73 066206
Google Scholar
[10] Wei L Y, Dong L F, Feng J Y, Liu W B, Fan W L, Pan Y Y 2016 J. Phys. D: Appl. Phys. 49 185203
Google Scholar
[11] Pagea K M, Maini P K, Monk N A M 2005 Physica D 202 95
Google Scholar
[12] Yang L F, Zhabotinsky A M, Epstein I R 2004 Phys. Rev. Lett. 92 198303
Google Scholar
[13] Li J, Wang H L, Ouyang Q 2014 Chaos 24 023115
Google Scholar
[14] Judd S L, Silber M 2000 Physica D 136 45
Google Scholar
[15] Turing A M 1952 Philos. Trans. R. Soc. London, Ser. B 237 37
Google Scholar
[16] Qian Y, Gao H Y, Yao C G, Cui X H, Ma J 2018 Chin. Phys. B 27 108902
Google Scholar
[17] Mikhailova A S, Showalter K 2006 Phys. Rep. 425 79
Google Scholar
[18] 张荣培, 王震, 王语, 韩子健 2018 67 050503
Google Scholar
Zhang R P, Wang Z, Wang Y, Han Z J 2018 Acta Phys. Sin. 67 050503
Google Scholar
[19] Zhang L S, Liao X H, Mi Y Y, Qian Y, Hu G 2014 Chin. Phys. B 23 078906
Google Scholar
[20] Míguez D G, Dolnik M, Epstein I R, Muñuzuri A P 2011 Phys. Rev. E 84 046210
Google Scholar
[21] Gambino G, Lombardo M C, Sammartino M 2014 Acta Appl. Math. 132 283
Google Scholar
[22] Dong L F, He Y F, Liu W L, Gao R L, Wang H F, Zhao H T 2007 Appl. Phys. Lett. 90 031504
Google Scholar
[23] Barrio R A, Varea C, Aragon J L, Maini P K 1999 Bull. Math. Biol. 61 483
Google Scholar
[24] Dong L F, Fan W L, Pan Y Y 2010 Plasma Sci. Technol. 12 172
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6817
- PDF Downloads: 58
- Cited By: 0
