-
In the recent years, the theory and technologies of electromagnetic computational imaging have been well developed and several novel imaging methods have been proposed, one of which is known as the microwave imaging under random field illumination. In order to solve the matrix equation of imaging model, the key of such an imaging system is to generate the random electromagnetic radiation field distribution, implementing the independent measurements under random field illuminations. In this work, an optimal microwave imaging system for the desired imaging region and resolution is theoretically analyzed and experimentally implemented. In the randomness analysis, the correlation between different measurements is evaluated by the singular value decomposition, which is also adopted as a criterion for choosing the optimal parameters of the imaging system. Based on random field illuminations generated by the least number of antenna elements, a full-rank matrix equation can be used to reconstruct the object by direct matrix inversion, which can be completed in nearly real-time once the system calibration is implemented in advance. The numerical simulation and experimental investigation are performed, and the results prove the effectiveness of the proposed optimal imaging system. By using the traditional array theory, it is found that for an N-element phase array, N illuminations with each element excited by a single frequency, equal amplitude and randomized 0 or
${\text{π}}$ phase signal will result in N independent measurements. Theoretically, any additional measurement under random illumination will be correlated with the previous N measurements. Since the random field illumination is obtained by array antennas with 1-bit random phase modulation, the power radiated by each transmitting element is not sacrificed, resulting in an optimal power efficiency of the imaging system compared with those of earlier metasurface-based imaging systems. Besides, a single frequency signal source is used in the system, which also realizes the optimal spectrum efficiency. In conclusion, there are two major innovations of the proposed imaging system: 1) the completely random field illuminations based on 1-bit phase modulation; 2) the approach to optimizing the system on desired demand. The compact and low-cost imaging system promises to have various imaging applications, such as public security and indoor localization.-
Keywords:
- microwave imaging /
- array antenna /
- random field /
- phase modulation
[1] Nikolova N 2017 Introduction to Microwave Imaging (Cambridge: Cambridge University Press) pp1–20
[2] Elsdon M, Smith D, Leach M, Foti S 2005 Microw. Opt. Techn. Lett. 47 536
[3] Ahmed S S, Schiessl A, Gumbmann F, Tiebout M, Methfessel S, Schmidt L P 2012 IEEE Microw. Mag. 13 26
[4] Laviada J, Wu B, Ghasr M T, Zoughi R 2018 IEEE Trans. Instrum. Meas. 99 1
[5] Di Meo S, Espín-López P F, Martellosio A, Pasian M, Matrone G, Bozzi M, Magenes G, Mazzanti A, Perregrini L, Svelto F, Summers P E, Renne G, Preda L, Bellomi M 2017 IEEE Trans. Microw. Theory Techn. 65 1795
Google Scholar
[6] BaranoskiE J 2008 J. Franklin Inst. 345 556
Google Scholar
[7] Bertero M, Boccacci P 1998 Introduction to Inverse Problems in Imaging (Bristol: Institute of Physics Pub.) pp1–11
[8] Wang Y M, Chew W C 1989 Int. J. Imaging Syst. Technol. 1 100
Google Scholar
[9] van den Berg P M, Kleinman R E 1997 Inv. Prob. 13 1607
Google Scholar
[10] Benedetti M, Franceschini G, Azaro R, Massa A 2007 Antennas Wirel. Propag. Lett. 6 271
Google Scholar
[11] Mojabi P, Lovetri J, Shafai L 2011 IEEE Trans. Antennas Propag. 59 4790
Google Scholar
[12] Chen X 2010 IEEE Trans. Geosci. Remote Sens. 48 42
Google Scholar
[13] Palmeri P, Martina B, Lorenzo C, Tommaso I, Loreto D 2017 IEEE Trans. Antennas Propag. 65 829
Google Scholar
[14] Xu K, Zhong Y, Chen X, Lesselier D 2018 IEEE Trans. Antennas Propag. 66 4228
Google Scholar
[15] Pastorino M 2010 Microwave Imaging (Hoboken N J: John Wiley) pp20–53
[16] Yurduseven O, Gollub J N, Marks D L, Smith D R 2016 Opt. Express 24 8907
Google Scholar
[17] Yurduseven O, Gowda V R, Gollub J N, Smith D R 2016 IEEE Microw. Compon. Lett. 26 367
Google Scholar
[18] Hunt J, Driscoll T, Mrozack A, Lipworth G, Reynolds M, Brady D, Smith D R 2013 Science 339 310
Google Scholar
[19] Lipworth G, Mrozack A, Hunt J, Marks D L, Driscoll T, Brady D, Smith D R 2013 J. Opt. Soc. Am. A 30 1603
Google Scholar
[20] Hunt J, Gollub J, Driscoll T, Lipworth G, Mrozack A, Reynolds M, Brady D, Smith D R 2014 J. Opt. Soc. Am. A 31 2109
[21] Sleasman T, Imani M F, Gollub J N, Smith D R 2015 Appl. Phys. Lett. 107 204104
Google Scholar
[22] Sleasman T, Boyarsk M, Imani M F, Gollub J N, Smith D R 2016 J. Opt. Soc. Am. B 33 1098
Google Scholar
[23] Sleasman T, Boyarsky M, Pulido-Mancera L, Fromenteze T, Imani M F, Reynolds M S, Smith D R 2017 IEEE Trans. Antennas Propag. 65 6864
Google Scholar
[24] Li Y, Li L, Xu, B, Wu W, Wu R, Wan X, Cheng Q, Cui T 2016 Sci. Rep. 6 23731
[25] Kong J A 1986 Theory of Electromagnetic Waves (New York: Wiley) pp225–229
[26] Donoho D L 2006 IEEE Trans. Inf. Theory 52 1289
[27] Massa A, Rocca P, Oliveri G 2015 IEEE Antennas Propag. Mag. 57 224
Google Scholar
[28] Hua Y, Sarkar T K 1991 IEEE Trans. Signal Process. 39 892
Google Scholar
[29] Fan T, Ma C, Gu Z, Lv Q, Chen J, Ye D, Huangfu J, Sun Y, Li C, Ran L 2016 IEEE Trans. Microw. Theory Techn. 64 4012
Google Scholar
-
图 1 基于随机场照射的成像系统示意图
Figure 1. Schematic diagram of the imaging system based on randomized field illuminations.
图 2 基于1 bit随机相位调制的成像系统框图
Figure 2. System-level diagram of the imaging system based on 1-bit randomizedphase modulation.
图 3 不同1 bit随机相位分布对应的H矩阵随机性分析
Figure 3. Randomness analysis of the H matrix for different 1-bit phase.
图 5 成像系统参数之间关系 (a)最优成像距离R与组阵间距Δ r、分辨率Δ r′之间的变化关系; (b)最优成像距离R与天线单元数量N、分辨率Δ r′之间的变化关系
Figure 5. Dependence analysis: (a) Dependence of the optimal imaging distance with respect to Δ r and Δ r′; (b) dependence of the optimal imaging distance with respect to Δ r′ and N when Δ r = 0.5
$\lambda $ .
图 4 随测量次数和成像距离变化的H矩阵奇异值分布曲线(a)以及25测量处的二维剖面(b)
Figure 4. (a) Dependence of the normalized singular value with respect to the measurement times M and the imaging distance R; (b) profiles of Fig. 4(a) for M = 25.
图 6 仿真设置 (a) “T”形目标; (b), (c)任意两次随机照射; (d) H矩阵的归一化奇异值
Figure 6. Simulation setup: (a) T-shaped object; (b), (c) randomized illuminations; (d) singular values of the H matrix.
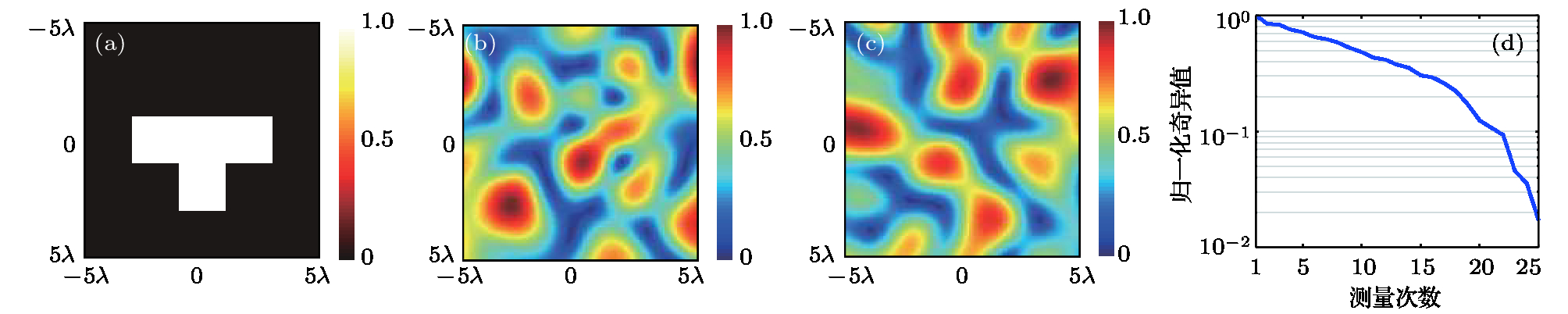
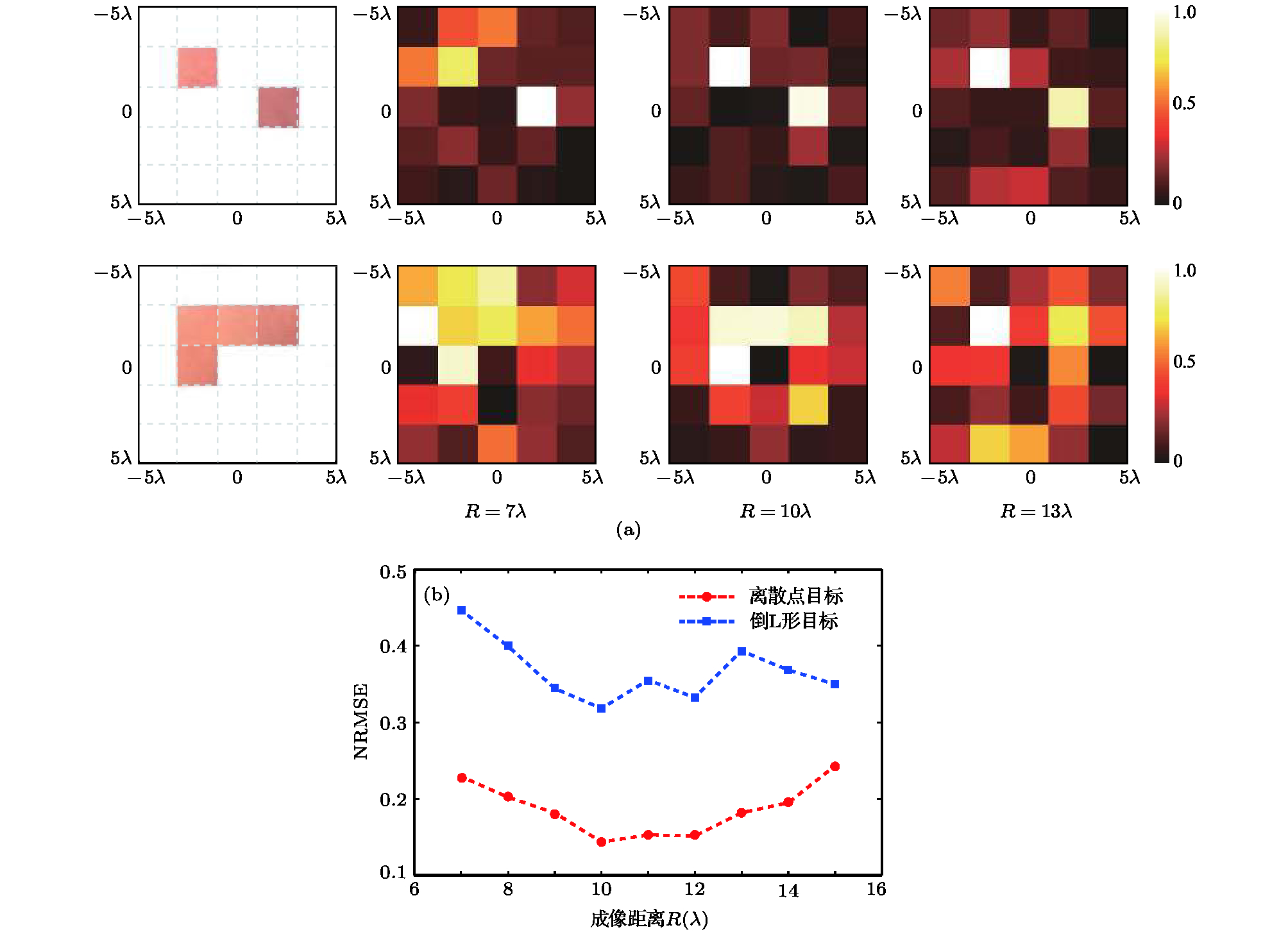
图 7 基于信噪比15 dB的仿真数据反演得到不同成像距离处的重建图像 (a) R = 5
$\lambda $ 的重建图像; (b) R = 10$\lambda $ 的重建图像; (c) R = 15$\lambda $ 的重建图像; (d)重建图像误差随成像距离的变化曲线Figure 7. Reconstructed images based on simulated data with a 15 dB SNR. Reconstructed images for imaging distances of 5
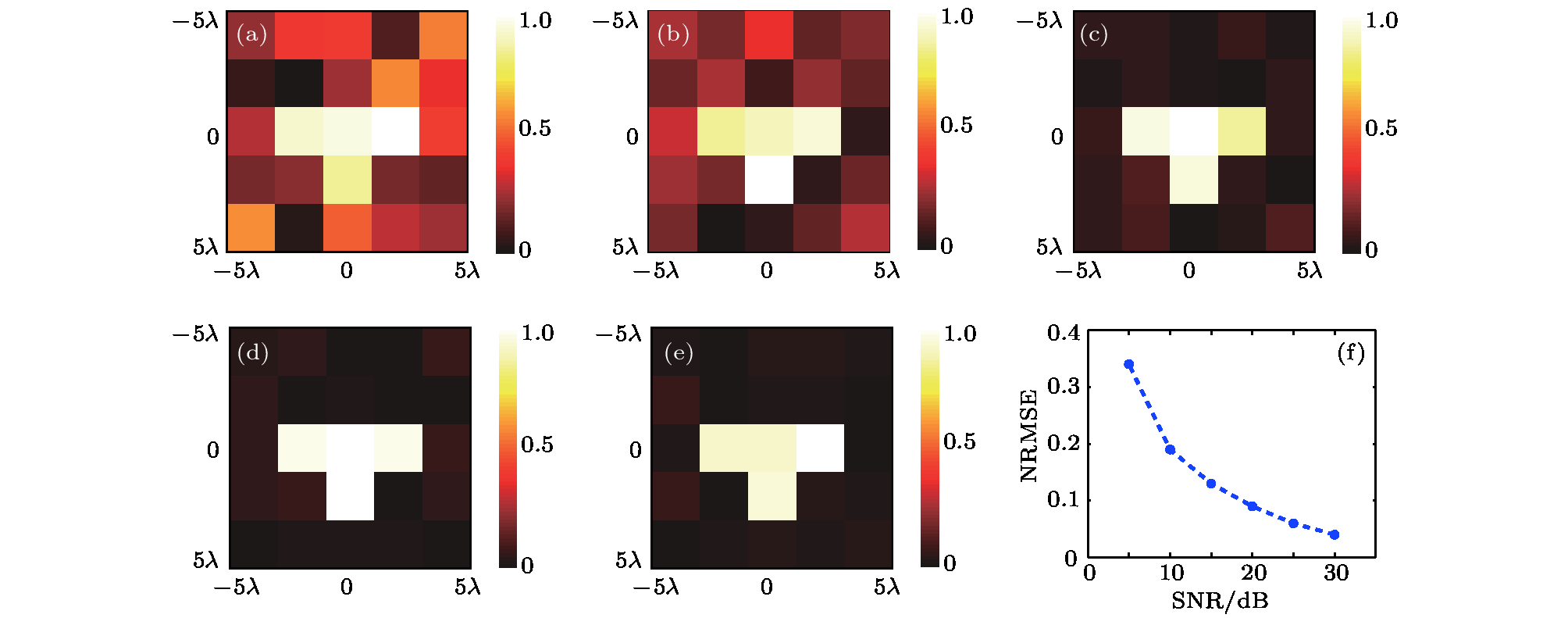
$\lambda $ (a), 10$\lambda $ (b) and 15$\lambda $ (c), respectively; (d) NRMSE analysis of images reconstructed with different imaging distances.
图 8 基于仿真数据反演得到不同信噪比下的重建图像 (a) SNR = 5 dB; (b) SNR = 10 dB; (c) SNR = 20 dB; (d) SNR = 25 dB; (e) SNR = 30 dB; (f) NRMSE分析
Figure 8. Reconstructed images based on simulated data with different SNRs. Reconstructed images with SNR values of 5 dB (a), 10 dB (b), 20 dB (c), 25 dB (d) and 30 dB (e), respectively; (f) NRMSE analysis.
图 9 1 bit相位调制器 (a)电路拓扑结构和测试板照片; (b)两种切换状态下实测幅度和相位
Figure 9. 1-bit phase modulator: (a) Topology and test board; (b) measured amplitude and phase difference.
图 10 成像实验系统的集成电路板照片
Figure 10. Photo of the board-integrated imaging system.
图 11 实测H矩阵的归一化奇异值
Figure 11. Normalized singular values of the H matrix using the measured data.
图 12 基于随机多波束照射的微波成像实验系统
Figure 12. Experimental setup of the imaging system based on random field illuminations.
图 14 在最优成像距离处的成像实验结果 (a)原始目标; (b)重建图像
Figure 14. Imaging results at the optimal distance using experimental data: (a) The original objects; (b) reconstructed images.
图 13 不同成像距离处的成像实验结果 (a)离散点目标和倒“L”形状目标在不同成像距离R的重建图像; (b)重建图像误差随成像距离R的变化曲线
Figure 13. Experimental results with different R: (a) Reconstructed imageof two discrete objectsand inverted L-shape objectat 7
$\lambda $ , 10$\lambda $ , and 13$\lambda $ distances, respectively; (b) NRMSE analysis. -
[1] Nikolova N 2017 Introduction to Microwave Imaging (Cambridge: Cambridge University Press) pp1–20
[2] Elsdon M, Smith D, Leach M, Foti S 2005 Microw. Opt. Techn. Lett. 47 536
[3] Ahmed S S, Schiessl A, Gumbmann F, Tiebout M, Methfessel S, Schmidt L P 2012 IEEE Microw. Mag. 13 26
[4] Laviada J, Wu B, Ghasr M T, Zoughi R 2018 IEEE Trans. Instrum. Meas. 99 1
[5] Di Meo S, Espín-López P F, Martellosio A, Pasian M, Matrone G, Bozzi M, Magenes G, Mazzanti A, Perregrini L, Svelto F, Summers P E, Renne G, Preda L, Bellomi M 2017 IEEE Trans. Microw. Theory Techn. 65 1795
Google Scholar
[6] BaranoskiE J 2008 J. Franklin Inst. 345 556
Google Scholar
[7] Bertero M, Boccacci P 1998 Introduction to Inverse Problems in Imaging (Bristol: Institute of Physics Pub.) pp1–11
[8] Wang Y M, Chew W C 1989 Int. J. Imaging Syst. Technol. 1 100
Google Scholar
[9] van den Berg P M, Kleinman R E 1997 Inv. Prob. 13 1607
Google Scholar
[10] Benedetti M, Franceschini G, Azaro R, Massa A 2007 Antennas Wirel. Propag. Lett. 6 271
Google Scholar
[11] Mojabi P, Lovetri J, Shafai L 2011 IEEE Trans. Antennas Propag. 59 4790
Google Scholar
[12] Chen X 2010 IEEE Trans. Geosci. Remote Sens. 48 42
Google Scholar
[13] Palmeri P, Martina B, Lorenzo C, Tommaso I, Loreto D 2017 IEEE Trans. Antennas Propag. 65 829
Google Scholar
[14] Xu K, Zhong Y, Chen X, Lesselier D 2018 IEEE Trans. Antennas Propag. 66 4228
Google Scholar
[15] Pastorino M 2010 Microwave Imaging (Hoboken N J: John Wiley) pp20–53
[16] Yurduseven O, Gollub J N, Marks D L, Smith D R 2016 Opt. Express 24 8907
Google Scholar
[17] Yurduseven O, Gowda V R, Gollub J N, Smith D R 2016 IEEE Microw. Compon. Lett. 26 367
Google Scholar
[18] Hunt J, Driscoll T, Mrozack A, Lipworth G, Reynolds M, Brady D, Smith D R 2013 Science 339 310
Google Scholar
[19] Lipworth G, Mrozack A, Hunt J, Marks D L, Driscoll T, Brady D, Smith D R 2013 J. Opt. Soc. Am. A 30 1603
Google Scholar
[20] Hunt J, Gollub J, Driscoll T, Lipworth G, Mrozack A, Reynolds M, Brady D, Smith D R 2014 J. Opt. Soc. Am. A 31 2109
[21] Sleasman T, Imani M F, Gollub J N, Smith D R 2015 Appl. Phys. Lett. 107 204104
Google Scholar
[22] Sleasman T, Boyarsk M, Imani M F, Gollub J N, Smith D R 2016 J. Opt. Soc. Am. B 33 1098
Google Scholar
[23] Sleasman T, Boyarsky M, Pulido-Mancera L, Fromenteze T, Imani M F, Reynolds M S, Smith D R 2017 IEEE Trans. Antennas Propag. 65 6864
Google Scholar
[24] Li Y, Li L, Xu, B, Wu W, Wu R, Wan X, Cheng Q, Cui T 2016 Sci. Rep. 6 23731
[25] Kong J A 1986 Theory of Electromagnetic Waves (New York: Wiley) pp225–229
[26] Donoho D L 2006 IEEE Trans. Inf. Theory 52 1289
[27] Massa A, Rocca P, Oliveri G 2015 IEEE Antennas Propag. Mag. 57 224
Google Scholar
[28] Hua Y, Sarkar T K 1991 IEEE Trans. Signal Process. 39 892
Google Scholar
[29] Fan T, Ma C, Gu Z, Lv Q, Chen J, Ye D, Huangfu J, Sun Y, Li C, Ran L 2016 IEEE Trans. Microw. Theory Techn. 64 4012
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8856
- PDF Downloads: 79
- Cited By: 0
