Development on quantum metrology with quantum Fisher information

Ren Zhi-Hong; Li Yan; Li Yan-Na; Li Wei-Dong

doi:10.7498/aps.68.20181965

Abstract

Quantum metrology is one of the hot topics in ultra-cold atoms physics. It is now well established that with the help of entanglement, the measurement sensitivity can be greatly improved with respect to the current generation of interferometers that are using classical sources of particles. Recently, Quantum Fisher information plays an important role in this field. In this paper, a brief introduction on Quantum metrology is presented highlighting the role of the Quantum Fisher information. And then a brief review on the recent developments for i) criteria of multi-particle entanglement and its experimental generation; ii) linear and non-linear atomic interferometers; iii) the effective statistical methods for the analysis of the experimental data.

Keywords:

Authors and contacts

Institute of Theoretical Physics, State Key Laboratory of Quantum Optics and Quantum Optics Devices, Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Li Wei-Dong, wdli@sxu.edu.cn

Funds: Project supported by the National Key R&D Program of China (Grant Nos. 2017YFA0304500, 2017YFA0304203), the National Natural Science Foundation of China (Grant No. 11874247), the 111 Plan of China (Grant No. D18001), the Hundred Talent Program of Shanxi Province, China (2018), and the Program of State Key Laboratory of Quantum Optics and Quantum Optics Devices, China (Grant No. KF201703).

FullText HTML : translate this paragraph

References

[1]	Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439 Google Scholar
[2]	Helstrom C W 1976 Quantum Detection and Estimation Theory (New York: Academic Press)
[3]	Giovannetti V S, Lioyd S, Maccone L 2006 Phys. Rev. Lett. 96 010401 Google Scholar
[4]	Pezzè L, Smerzi A 2014 Atom Interferometry, Proceedings of the International School of Physics, " Enrico Fermi” Course 188, Varenna, p691
[5]	Pezzè L, Smerzi A, Oberthaler M K, Schmied R, Treutlein P 2018 Rev. Mod. Phys. 90 035005 Google Scholar
[6]	Caves C M 1981 Phys. Rev. D 23 1693 Google Scholar
[7]	Wineland D J, Bollinger J J, Itano W M, Heinzen D J 1994 Phys. Rev. A 50 67 Google Scholar
[8]	Yurke B, McCall S L, Klauder J R 1986 Phys. Rev. A 33 4033 Google Scholar
[9]	Zou Y Q, Wu L N, Liu Q, Luo X Y, Guo S F, Cao J H, Tey M K, You L 2018 Proc. Natl. Acad. Sci. U.S.A. 115 6381 Google Scholar
[10]	Kruse I, Lange K, Peise J, Lücke B, Pezzè L, Arlt J, Ertmer W, Lisdat C, Santos L, Smerzi A, Klempt C 2016 Phys. Rev. Lett. 117 143004 Google Scholar
[11]	Muessel W, Strobel H, Linnemann D, Zibold T, Juliá-Dĺaz B, Oberthaler M K 2015 Phys. Rev. A 92 023603 Google Scholar
[12]	Muessel W, Strobel H, Linnemann D, Hume D B, Oberthaler M K 2014 Phys. Rev. Lett. 113 103004 Google Scholar
[13]	Strobel H, Muessel W, Linnemann D, Zibold T, Hume D B, Pezze L, Smerzi A, Oberthaler M K 2014 Science 345 424 Google Scholar
[14]	Ockeloen C F, Schmied R, Riedel M F, Treutlein P 2013 Phys. Rev. Lett. 111 143001 Google Scholar
[15]	Berrada T, Van Frank S, Bücker R, Schumm T, Schaff J F, Schmiedmayer J 2013 Nat. Commun. 4 2077 Google Scholar
[16]	Hamley C D, Gerving C S, Hoang T M, Bookjans E M, Chapman M S 2012 Nat. Phys. 8 305 Google Scholar
[17]	Lücke B, Scherer M, Kruse J, Pezzè L, Deuretzbacher F, Hyllus P, Topic O, Peise J, Ertmer W, Arlt J, Santos L, Smerzi A, Klempt C 2011 Science 334 773 Google Scholar
[18]	Riedel M F, Böhi P, Li Y, Hänsch T W, Sinatra A, Treutlein P 2010 Nature 464 1170 Google Scholar
[19]	Gross C, Zibold T, Nicklas E, Estève J, Oberthaler M K 2010 Nature 464 1165 Google Scholar
[20]	Estève J, Gross C, Weller A, Giovanazzi S, Oberthaler M K 2008 Nature 455 1216 Google Scholar
[21]	Giovannetti V, LIoyd S, Maccone L 2004 Science 306 1330 Google Scholar
[22]	Cronin A, Schmiedmayer J, Pritchard D E 2009 Rev. Mod. Phys. 81 1051 Google Scholar
[23]	Peters A, Chung K Y, Chu S 1999 Nature 400 849 Google Scholar
[24]	Peters A, Chung K Y, Chu S 2001 Metrologia 38 25 Google Scholar
[25]	Zhou L, Xiong Z Y, Yang W, Tang B A, Peng W C, Wang Y B, Xu P, Wang J, Zhan M S 2011 Chin. Phys. Lett. 28 013701 Google Scholar
[26]	Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 043610 Google Scholar
[27]	Gustavson T L, Bouyer P, Kasevich M A 1997 Phys. Rev. Lett. 78 2046 Google Scholar
[28]	Geiger R, Menort V, Stern G, Zahzam N, Cheinet P, Batelier B, Villing A, Moron F, Lours M, Bidel Y, Bresson A, Landragin A, Bouyer P 2011 Nat. Commun. 2 474 Google Scholar
[29]	Ekstrom C R, Schmiedmayer J, Chapman M S, Hammond T D, Pritchard D E 1995 Phys. Rev. A 51 3883 Google Scholar
[30]	Fixler J, Foster G, McGuirk J, Kasevich M A 2007 Science 315 74 Google Scholar
[31]	Lamporesi G, Bertoldi A, Cacciapuoti L, Prevedelli M, Tino G M 2008 Phys. Rev. Lett. 100 050801 Google Scholar
[32]	Bouchendira R, Clade P, Guellati-Khelifa S, Nez F, Biraben F 2011 Phys. Rev. Lett. 106 080801 Google Scholar
[33]	Rosi G, Sorrentino F, Cacciapuoti L, Prevedelli M, Tino G M 2014 Nature 510 518 Google Scholar
[34]	Parker R H, Yu C H, Zhong W C, Estey B, Müller H 2018 Science 360 191 Google Scholar
[35]	叶朝辉 2018 67 16 Ye Z H 2018 Acta Phys. Sin. 67 16
[36]	Ramesy N F 1949 Phys. Rev. 76 996
[37]	Ramesy N F 2005 Metrologia 42 S01
[38]	林弋戈, 方占军 2018 67 160604 Google Scholar Lin Y G, Fang Z J 2018 Acta Phys. Sin. 67 160604 Google Scholar
[39]	孙昌璞 2017 物理 46 481 Google Scholar Sun C P 2017 Physics 46 481 Google Scholar
[40]	Maxwell J C 1873 Treatise on Electricity and Magnetism (Oxford: Clarendon)
[41]	Ramesy N F 1956 Molecular Beams (Oxford: Oxford University Press)
[42]	Rabi I I 1937 Phys. Rev. 51 652 Google Scholar
[43]	Riehle F 2004 Frequency Standards: Basics and Applications (Wiley-VCH Verlag GmbH Co. KGaA)
[44]	管桦, 黄垚, 李承斌, 高克林 2018 67 164202 Google Scholar Guan H, Huang Y, Li C B, Gao K L 2018 Acta Phys. Sin. 67 164202 Google Scholar
[45]	Caves C M 1981 Phys. Rev. D 23 1693
[46]	Wineland D J, Bollinger J J, Itano W M, Morre F L, Heinzen D J 1992 Phys. Rev. A 46 R6797 Google Scholar
[47]	Pezzè L, Smerzi A 2009 Phys. Rev. Lett. 102 100401 Google Scholar
[48]	Toth G 2012 Phys. Rev. A 85 022322 Google Scholar
[49]	Braun D, Adesso G, Benatti F, Floreanini R, Marzolino U, Mitchell M W, Pirandola S 2018 Rev. Mod. Phys. 90 035006 Google Scholar
[50]	Zanardi P, Paris M G A, Venuti L C 2008 Phys. Rev. A 78 042105 Google Scholar
[51]	Invernizzi C, Korbman M, Venuti L C, Paris M G A 2008 Phys. Rev. A 78 042106 Google Scholar
[52]	Ma J, Wang X G 2009 Phys. Rev. A 80 012318 Google Scholar
[53]	Wang T L, Wu L N, Yang W, Jin G R, Lambert N, Nori F 2014 New J. Phys. 16 063039 Google Scholar
[54]	Gabbrielli M, Smerzi A, Pezzè L 2018 Sci. Rep. 8 15663 Google Scholar
[55]	Hauke P, Heyl M, Tagliacozzo L, Zoller P 2016 Nat. Phys. 12 778 Google Scholar
[56]	Pezzè L, Gabbrielli M, Lepori L, Smerzi A 2017 Phys. Rev. Lett. 119 250401 Google Scholar
[57]	Sun Z, Ma J, Lu X M, Wang X G 2010 Phys. Rev. A 82 022306 Google Scholar
[58]	Liu W F, Ma J, Wang X G 2013 J. Phys. A: Math. Theor. 46 045302 Google Scholar
[59]	Huang Y X, Zhong W, Sun Z, Wang X G 2012 Phys. Rev. A 86 012320 Google Scholar
[60]	Rao C R 1945 Bull. Calcutta Math. Soc. 37 81
[61]	Camer H 1946 Mathematical Methods of Statistics (Princeton: Princeton University Press)
[62]	Frechet M 1943 Rev. Internat. Stat. Inst. 11 182 Google Scholar
[63]	Darmoois G 1945 Rev. Internat. Stat. Inst. 13 9 Google Scholar
[64]	Fisher R A 1922 Proc. R. Soc. Edinburgh 42 321
[65]	Braunstein S L Caves C M, Milburn G J 1996 Ann. Phys. (N. Y.) 247 135 Google Scholar
[66]	Helstrom C W 1967 Phys. Lett. A 25 101 Google Scholar
[67]	Holevo A S 1982 Probabilistic and Statistical Aspects of Quantum Theory (Amsterdam: North-Holland)
[68]	Paris M G A 2009 Int. J. Quantum Inf. 7 125 Google Scholar
[69]	Wiseman H M, Milburn G J 2010 Quantum Measurement and Control (Cambridge: Combridge University Press)
[70]	Barndorff-Nielsen O E, Gill R D 2000 J. Phys. A 33 4481 Google Scholar
[71]	Zhong W, Huang Y X, Wang X G, Zhu S L 2017 Phys. Rev. A 95 052304 Google Scholar
[72]	Cohen M L 1968 IEEE Trans. Inf. Theory 14 591 Google Scholar
[73]	Liu J, Jing X X, Wang X G 2013 Phys. Rev. A 88 042316 Google Scholar
[74]	Zhang Y M, Li X W, Yang W, Jin G R 2013 Phys. Rev. A 88 043832 Google Scholar
[75]	Liu J, Jing X X, Zhong W, Wang X G 2014 Commun. Theor. Phys. 61 45 Google Scholar
[76]	Liu J, Chen j, Jing X X, Wang X G 2016 J. Phys. A 49 275302 Google Scholar
[77]	Pang S S, Brun T A 2014 Phys. Rev. A 90 022117 Google Scholar
[78]	Liu J, Jing X X, Wang X G 2015 Sci. Rep. 5 8565 Google Scholar
[79]	Zhong W, Sun Z, Ma J, Wang X G, Nori F 2013 Phys. Rev. A 87 022337 Google Scholar
[80]	Uys H, Meystre P 2007 Phys. Rev. A 76 013804 Google Scholar
[81]	Zhong W, Lu X M, Jing X X, Wang X G 2014 J. Phys. A: Math. Theor. 47 385304 Google Scholar
[82]	Gessner M, Pezze L, Smerzi A 2016 Phys. Rev. A 94 020101 Google Scholar
[83]	Wootters W K 1981 Phys. Rev. D 23 357 Google Scholar
[84]	Pezzè L, Li Yan, Li Weidong, Smerzi A 2016 Proc. Natl. Acad. Sci. U. S. A. 113 11459 Google Scholar
[85]	Braunstein S L, Lane A S, Caves C M 1992 Phys. Rev. Lett. 69 2153 Google Scholar
[86]	Li Y, Li W D 2018 Physica A 514 606
[87]	Liu J, Xiong H N, Song F, Wang X G 2014 Physica A 410 167 Google Scholar
[88]	Tommaso M, Augusto S, Luca P 2016 Phys. Rev. A 94 010102(R)Google Scholar
[89]	Wineland D J 2013 Rev. Mod. Phys. 85 1103 Google Scholar
[90]	Leibfried D, Blatt R, Monroe, Wineland D J 2003 Rev. Mod. Phys. 75 281 Google Scholar
[91]	Leibfried D, et. al. 2005 Nature 438 639 Google Scholar
[92]	Monz T, Schindler P, Barreiro J T, Chwalla M, Nigg D, Coish W, Harlander M H W, Hennrich M, Blatt R 2011 Phys. Rev. Lett. 106 130506 Google Scholar
[93]	Bollinger J J, Wayne M Itano, Wineland D J, Heinzen D J 1996 Phys. Rev. A 54 R4649 Google Scholar
[94]	Gerry C C, Mimih J 2010 Contemp. Phys. 51 497 Google Scholar
[95]	Leibfried D, et. al. 2004 Science 304 1476 Google Scholar
[96]	Walther P, et al. 2004 Nature 429 158 Google Scholar
[97]	Gao W B, et al. 2010 Nat. Phys. 6 331 Google Scholar
[98]	Wemer R F 1989 Phys. Rev. A 40 4277 Google Scholar
[99]	Gühne O, Tòth G 2009 Phys. Rep. 474 1 Google Scholar
[100]	Hyllus P, Laskowski W, Krischek R, Schwemmer C, Wieczorek W, Weinfurter H, Pezzè L, Smerzi A 2012 Phys. Rev. A 85 022321 Google Scholar
[101]	Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865 Google Scholar
[102]	Dur W, Vidal G, Cirac J I 2000 Phys. Rev. A 62 062314 Google Scholar
[103]	Gühne O, Tòth G, Briegel H J 2005 New. J. Phys. 7 229 Google Scholar
[104]	Sorensen A S, Kolmer K 2001 Phys. Rev. Lett. 86 4431 Google Scholar
[105]	Holland M J, Burnett 1993 Phys. Rev. Lett. 71 1355 Google Scholar
[106]	Lane A S, Braunstein S L, Caves C M 1993 Phys. Rev. A 47 1667 Google Scholar
[107]	Pezzè L, Smerzi A 2013 Phys. Rev. Lett. 110 163604 Google Scholar
[108]	Barreiro J T, et al. 2013 Nat. Phys. 9 559 Google Scholar
[109]	Luo X Y, Zou Y Q, Wu L N, Liu Q, Fan M F, Tey M K, You L 2017 Science 355 620 Google Scholar
[110]	Zeng Y, Xu P, He X, Liu Y Y, Liu M, Wang J, Papoular D J, Shlyapnikov G V, Zhan M S 2017 Phys. Rev. Lett. 119 160502 Google Scholar
[111]	Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
[112]	Amico L, Fazio R, Osterloh A, Vedral V 2008 Rev. Mod. Phys. 80 517 Google Scholar
[113]	Ma J, Wang X, Sun C P, Nori F 2011 Phys. Rep. 509 89 Google Scholar
[114]	Pan J W, Chen Z B, Lu C Y, Weinfurter H, Zeilinger A, Żukowski M 2012 Rev. Mod. Phys. 84 777 Google Scholar
[115]	Gühne O, Tòth G 2009 Phys. Rep. 474 1
[116]	Zhang Z, Duan L M 2013 Phys. Rev. Lett. 111 180401 Google Scholar
[117]	Zhang W, Zhou D L, Chang M S, Chapman M S, You L 2005 Phys. Rev. A 72 013602 Google Scholar
[118]	郑盟锟, 尤力 2018 67 160303 Google Scholar Tey M K, You L 2018 Acta Phys. Sin. 67 160303 Google Scholar
[119]	Feldmann P, Gessner M, Gabbrielli M, Klempt C, Santos L, Pezze L, Smerzi A 2018 Phys. Rev. A 97 032339 Google Scholar
[120]	Pezze L, Gessner M, Feldmann P, Klempt C, Santos L, Smerzi A 2017 arXiv: quant-ph 1712.03864v1
[121]	Brunner N, Cavalcanti D ironio S, Scarani V, Wehner S 2014 Rev. Mod. Phys. 86 419 Google Scholar
[122]	Li Y, Gessner M, Li Weidong, Smerzi A 2018 Phys. Rev. Lett. 120 050404 Google Scholar
[123]	Galitski V, Spielman I B 2013 Nature 494 49 Google Scholar
[124]	Zhai H 2015 Rep. Prog. Phys. 78 026001 Google Scholar
[125]	Yurke B 1986 Phys. Rev. Lett. 56 1515 Google Scholar
[126]	Zhou M, Duan X, Chen L, Luo Q, Xu Y, Hu Z 2015 Chin. Phys. B 24 050401 Google Scholar
[127]	Gabbrielli M, Pezzè L, Smerzi A 2015 Phys. Rev. Lett. 115 163002 Google Scholar
[128]	Moskowitz P, Gould P, Altas S, Pritchard D 1983 Phys. Rev. Lett. 51 370 Google Scholar
[129]	Ovchinikov Y B, Muller J H, Doery M R, Vredenbregt E J D, Helmerson K, Rolston S L, Phillips W D 1999 Phys. Rev. Lett. 83 284 Google Scholar
[130]	冯啸天, 袁春华, 陈丽清, 陈洁菲, 张可烨, 张卫平 2018 67 164204 Google Scholar Feng X T, Yuan C H, Chen L Q, Chen J F, Zhang K Y, Zhang W P 2018 Acta Phys. Sin. 67 164204 Google Scholar
[131]	Fray S, Diez C A, Hansch T W, Weitz M 2004 Phys. Rev. Lett. 93 240404 Google Scholar
[132]	Schlippert D, Hartwig J, Albers H, Richardson L L, Schubert C, Roura A, Schleich W P, Ertmer W, Rasel E M 2014 Phys. Rev. Lett. 112 203002 Google Scholar
[133]	Tarallo M G, Mazzoni T, Poli N, Sutyrin D V, Zhang X, Tino G M 2014 Phys. Rev. Lett. 113 023005 Google Scholar
[134]	Zhou L, Long S T, Tang B, Chen X, Gao F, Peng W C, Duan W T, Zhong J Q, Xiong Z Y, Wang J, Zhang Y Z, Zhan M S 2015 Phys. Rev. Lett. 115 013004 Google Scholar
[135]	Barrett B, Antoni-Micollier L, Chichet L, Battelier B, Leveque T, Landragin A, Bouyer P 2016 Nat. Commun. 7 13786 Google Scholar
[136]	Duan X C, Deng X B, Zhou M K, Zhang K, Xu W J, Xiong F, Xu Y Y, Shao C G, Luo J, Hu Z K 2016 Phys. Rev. Lett. 117 023001 Google Scholar
[137]	Rosi G, DAmico G, Cacciapuoti L, Sorrentino F, Prevedelli M, Zych M, Brukner Č, Tino G M 2017 Nat. Commun. 8 15529 Google Scholar
[138]	王谨, 詹明生 2018 67 160402 Google Scholar Wang J, Zhan M S 2018 Acta Phys. Sin. 67 160402 Google Scholar
[139]	Kasevich M, Chu S 1992 Appl. Phys. B 54 321 Google Scholar
[140]	Li W, He T, Smerzi A 2014 Phys. Rev. Lett. 113 023003 Google Scholar
[141]	Zernike F 1950 J. Opt. Soc. Am. 40 326 Google Scholar
[142]	D’Ariano G M, Paris M G A 1997 Phys. Rev. A 55 2267 Google Scholar
[143]	Chwedenczuk J, Piazza F, Smerzi A 2013 Phys. Rev. A 87 033607 Google Scholar
[144]	王倩, 魏荣, 王育竹 2018 67 163202 Google Scholar Wang Q, Wei R, Wang Y Z 2018 Acta Phys. Sin. 67 163202 Google Scholar
[145]	Cheng R, He T, Li W, Smerzi A 2016 J. Mod. Phys. 7 2043 Google Scholar
[146]	Ferrari G, Poli N, Sorrentino F, Tino G M 2006 Phys. Rev. Lett. 97 060402 Google Scholar
[147]	Luis A 2004 Phys. Lett. A 329 8 Google Scholar
[148]	Boixo S, Datta A, Flammia S T, Shaji A, Bagan E, Caves C M 2008 Phys. Rev. A 77 012317 Google Scholar
[149]	Boixo S, Datta A, Davis M J, Flammia S T, Shaji A, Caves C M 2008 Phys. Rev. Lett. 101 040403 Google Scholar
[150]	Woolley M J, Milburn G J, Caves C M 2008 New J. Phys. 10 125018 Google Scholar
[151]	Roy S M, Braunstein S L 2008 Phys. Rev. Lett. 100 220501 Google Scholar
[152]	Napolitano M, Mitchell M W 2010 New J. Phys. 12 093016 Google Scholar
[153]	Napolitano M, Koschorreck M, Dubost B, Behbood N, Sewell R J, Mitchell M W 2011 Nature 471 486 Google Scholar
[154]	Schaub P, et al. 2015 Science 347 1455 Google Scholar
[155]	Lipkin H J, Meshkov N, Glick A J 1965 Nucl. Phys. 62 188 Google Scholar
[156]	Meshkov N, Glick A J, Lipkin H J 1965 Nucl. Phys. 62 199 Google Scholar
[157]	Glick A J, Lipkin H J, Meshkov N 1965 Nucl. Phys. 62 211 Google Scholar
[158]	Dusuel S, Vidal J 2004 Phys. Rev. Lett. 93 237204 Google Scholar
[159]	Dusuel S, Vidal J 2005 Phys. Rev. B 71 224420 Google Scholar
[160]	Wichterich H, Vidal J, Bose S 2010 Phys. Rev. A 81 032311 Google Scholar
[161]	Ma J, Wang X 2009 Phys. Rev. A 80 012318
[162]	Salvatori G, Mandarino A, Paris M G A 2014 Phys. Rev. A 90 022111 Google Scholar
[163]	VanTrees H L, Bell K L, Tian Z 2013 Detection, Estimation and modulation theory (WILEYINTERSCIENCE A JOHN WILEY and SONS, INC., PUBLICATION)
[164]	Li Y, Pezzè L, Gessner M, Ren Z H, Li W D, Smerzi A 2018 Entropy 20 628 Google Scholar
[165]	Hayashi M 2005 Asymptotic Theory of Quantum Statistical Inference, Selected Papers (Singapore:World Scientific Publishing)
[166]	Lehmann E L, Casella G 1998 Theory of Point Estimation (Berlin: Springer）
[167]	Barankin E W 1949 Ann. Math. Stat. 20 477 Google Scholar
[168]	Mcaulay R J, Hofstetter E M 1971 IEEE Trans. Inf. Theory 17 669 Google Scholar
[169]	Hammersley J M 1950 J. Roy. Statist. Soc. Ser. B 12 192
[170]	Chapman D G, Robbins H 1951 Ann. Math. Statist. 22 581 Google Scholar
[171]	Sivia D S, Skilling J 2006 Data Analysis: A Bayesian Tutorial (London: Oxford University Press)
[172]	Ghosh M 1993 Stat. Prob. Lett. 17 173 Google Scholar
[173]	Kay S M 1993 Fundamentals of Statistical Signal Processing: Estimation Theory(Volume I) (New Jersey: Prentice Hall)
[174]	Gessner M, Pezzè , Smerzi A 2016 Phys. Rev. A 94 020101
[175]	Gessner M, Pezze L, Smerzi A 2017 Quantum 1 17 Google Scholar
[176]	Qin Z Z, Gessner M, Ren Z H, Deng X, Han D, Li W D, Su X L, Smerzi A, Peng K C 2019 npj Quantum Inf. 5 3 Google Scholar
[177]	Suzuki J 2016 J. Math. Phys. 57 042201 Google Scholar
[178]	Pezzè L, Ciampini M A, Spagnolo N, Humphreys P C, Datta A, Walmsley I A, Barbieri M, Sciarrino F, Smerzi A 2017 Phys. Rev. Lett. 119 130504 Google Scholar
[179]	Gessner M, Pezze L, Smerzi A 2018 Phys. Rev. Lett. 121 130503 Google Scholar
[180]	Zhuang M, Huang J, Lee C H 2018 Phys. Rev. A 98 033603 Google Scholar
[181]	Tsang M, Wiseman H M, Caves C M 2011 Phys. Rev. Lett. 106 090401 Google Scholar
[182]	Liu J, Yuan H D 2016 New J. Phys. 18 093009 Google Scholar
[183]	Tsang M 2012 Phys. Rev. Lett. 108 230401 Google Scholar
[184]	Lu X M, Tsang M 2016 Quantum Sci. Technol. 1 015002 Google Scholar

Cited By

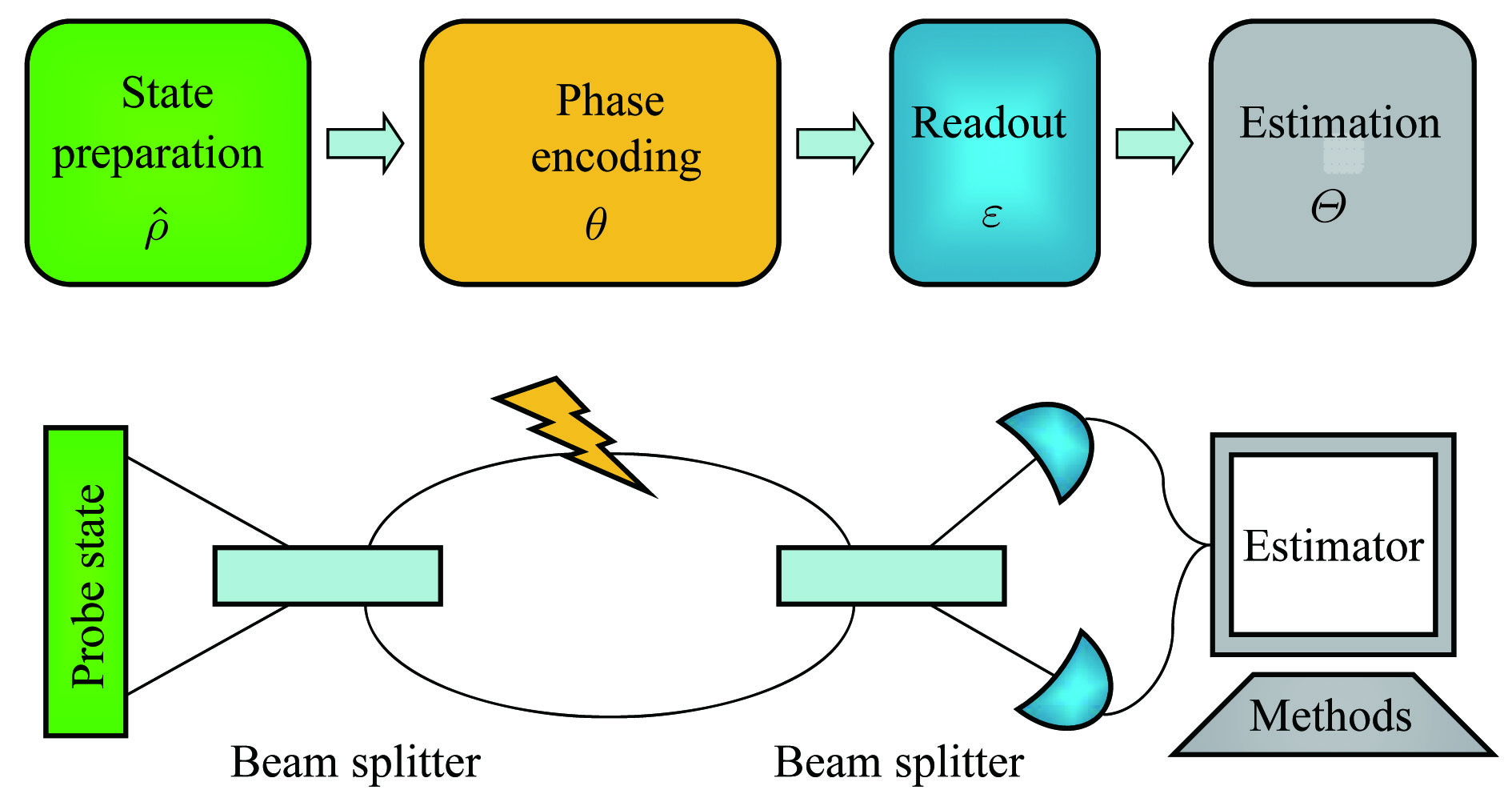
图 1 相位估计的流程示意图　(1) 探测量子初态$\hat{\rho}$的制备; (2)待测相位$\theta$的编码, 量子初态演化为$\hat{\rho}(\theta)$; (3) 正定的测量算符(POVM)对末态进行测量; (4)待测相位的统计估计${\varTheta}$. 图的下部分是马赫曾德(Mach-Zehnder, MZ)干涉仪的应用实例. 图取自文献[4]

Figure 1. Here we schematically plot the elements of complete phase estimation: (1) the preparation of prob state $\hat{\rho}(0)$; (2) the encoding of phase shift $\theta$, which transform the probe state to $\hat{\rho}(\theta)$; (3) the readout measurement of the POVM and finally (4) the mapping from the measurement results to the phase provided by the estimator ${\varTheta}$. The phase sensitivity crucially depends on all these operations. The lower panel shows the application to Mach-Zehnder interferometry. Adapted from Ref. [4].

DownLoad: Full-Size Img PowerPoint

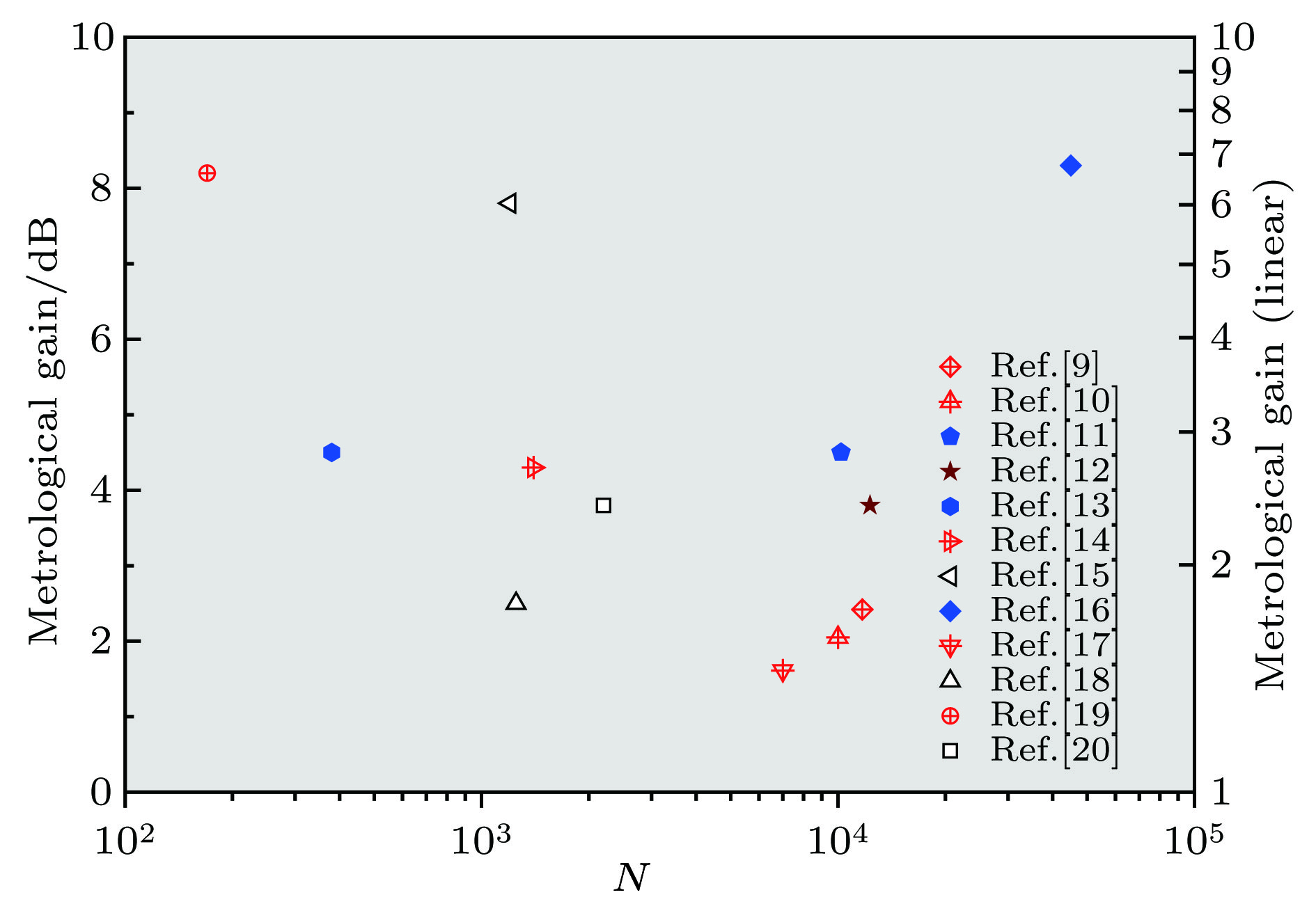
图 2 近年来利用超冷原子体系取得的超越标准量子极限的实验进展. 对数增益(左): $10\log_{10} ({\text{Δ}}\theta_{\rm{SQL}} / {\text{Δ}}\theta)^2$ 和对应的线性增益(右): $({\text{Δ}}\theta_{\rm{SQL}} / {\text{Δ}}\theta)^2$, 其中$({\text{Δ}}\theta)^2 = {\text{ξ}}_{\rm R}^2/N$或者$({\text{Δ}}\theta)^2 = 1/F_{\rm Q}$, ${\text{ξ}}_{\rm R}^2$为自旋压缩参数, $F_{\rm Q}$为量子Fisher信息. 空心图标为净增益, 即去除测量误差的增益; 实心图标为可能增益，即实验纠缠态的可能增益; 十字交叉图标为干涉仪增益，即通过干涉仪验证的增益. $N$为实验中所用的总粒子数目(或平均数目). 图取自文献[5]

Figure 2. Gain of phase sensitivity over the standard quantum limit $\Delta\theta_{\rm{SQL}}=1/\sqrt{N}$ achieved form recent Bose-Einstein condensates experiments. The logarithmic gain is shown in left, $10\log_{10} ({\text{Δ}}\theta_{\rm{SQL}} / {\text{Δ}}\theta)^2$ and the linear gain is in right, $({\text{Δ}}\theta_{\rm{SQL}} / {\text{Δ}}\theta)^2$. The measured phase precision is obtained by spin-squeezing parameter ${\text{ξ}}_{\rm R}^2$, i.e., $({\text{Δ}}\theta)^2 = {\text{ξ}}_{\rm R}^2/N$, or from $F_{\rm Q}$, i.e., $({\text{Δ}}\theta)^2=1/F_{\rm Q}$. Open patterns are inferred values, being obtained after subtraction of detection noise; Filled patterns report witnesses of metrologically useful entanglement measured on experimentally generated states, representing potential improvement in sensitivity; Cross patterns show the measured phase sensitivity gain obtained from a full interferometer sequence. Here $N$ is the total number of particles (or mean total) used in experiments. Adapted from Ref. [5].

DownLoad: Full-Size Img PowerPoint

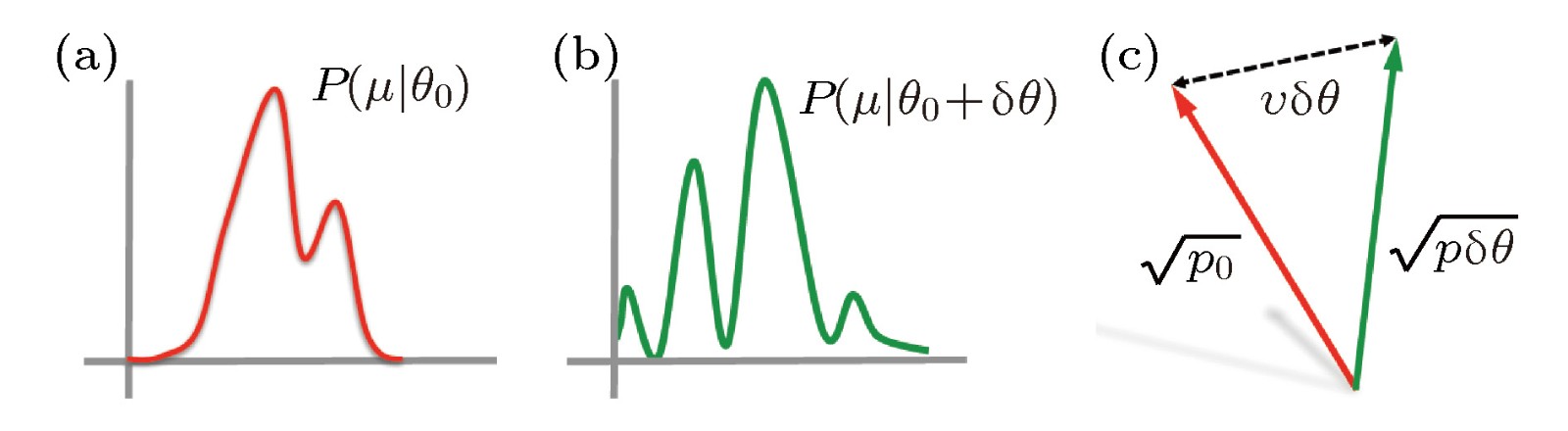
图 3 统计区分度和统计速度的示意图. 在给定$\theta_0$的条件下, 分析测量数据可得分布函数$p({\mu}|\theta_0)$(图(a)红线)和调节$\theta_0+\text{δ}\theta$后得分布函数$p({\mu}|\theta_0+\text{δ}\theta)$ (图(b)绿线). 图(c)示意由$\sqrt{p_0}=\sqrt{p({\mu}|\theta_0)}$和$\sqrt{p_{\text{δ}\theta}}=\sqrt{p({\mu}|\theta_0+\text{δ}\theta)}$定义的态矢量及其欧几里得距离(统计距离)$d_{\rm H}=2\|\sqrt{p_0}-\sqrt{p_{\text{δ}\theta}}\|$, 其中$v=v_{\rm H}$是衡量统计区分度的统计速度. 图取自文献[84]

Figure 3. Here we give the sketch of statistical distinguishability and statistical speed. The probability distribution $p({\mu}|\theta_0)$ is obtained by collecting the measurement results ${\mu}$ for different values of the parameter, here chosen to be $\theta_0$(red line) (a) and $\theta_0+\text{δ}\theta$ (green line)(b). (c) to quantify the statistical distinguishability between the two distributions we introduce unit vectors $\sqrt{p_0}=\sqrt{p({\mu}|\theta_0)}$ (red) and $\sqrt{p_{\text{δ}\theta}}=\sqrt{p({\mu}|\theta_0+\delta\theta)}$ (green), then we obtain the Euclidean distance between them: $d_{\rm H}=2\|\sqrt{p_0}-\sqrt{p_{\text{δ}\theta}}\|$. Here the $v=v_{\rm H}$ denotes the statistical speed. Adapted from Ref. [84].

DownLoad: Full-Size Img PowerPoint

图 4 海林格距离$d_{\rm H}^2$(红线)和KL熵$2D_{\rm {KL}}$(绿线), 以及他们共同的二阶展开项$F(\theta)\text{δ}\theta^2$(蓝线)的比较. 图取自文献[84]

Figure 4. Hellinger distance, $d_{\rm H}^2$(red line), KL entropy, $2D_{\rm {KL}}$(green line), and their common low-order approximation, $F(\theta)\text{δ}\theta^2$(blue line), as a function of $\theta$. Adapted from Ref. [84].

DownLoad: Full-Size Img PowerPoint

图 5 宇称振荡的测量结果和提取的Fisher信息　(a) GHZ($N=8$)的宇称测量图, 周期为$2\pi/8$, 取自文献[92]; (b) 基于近期实验结果得到的Fisher信息与总粒子数$N$的关系$F=V^2N^2$, 其中$V$为实验中的对比度. 上边界粗线为海森堡极限, 即$F=N^2$, 下边界黑色粗线代表标准量子极限, $F=N$. 图中其他的细线分别表示$k$粒子纠缠的边界, 即方程(60). 其中$N=10$的圆圈表明$4$粒子纠缠. 图取自文献[84]

Figure 5. Experimental results based on parity measurement and extracted Fisher information： (a) Typical parity oscillations obtained with cat states. The period is $2\pi/8$. Adapted from [92]; (b) summary of the experimental achievements, ions (circle) and photons (square). Here we show the Fisher information as a function of the number of qubits $N$, $F=V^2N^2$, obtained from the extracted experimental visibilities $V$. The upper thick line is the Heisenberg limit $F=N^2$, the lower thick line is the standard quantum limit, $F=N$. The different lines are bounds for useful $k$-particle entanglement, Eq. (60).For instance, the filled circle at $N=10$ reveals useful $4$-particle entanglement. Adapted from Ref. [84].

DownLoad: Full-Size Img PowerPoint

图 6 有利于量子计量的$k$粒子纠缠判据. 图中蓝色的实线由方程(60)给出: $k$粒子纠缠态的量子Fisher信息. 虚线为$F_{\rm Q}/N=k$, 其中粒子数$N=100$. 该图取自文献[100]

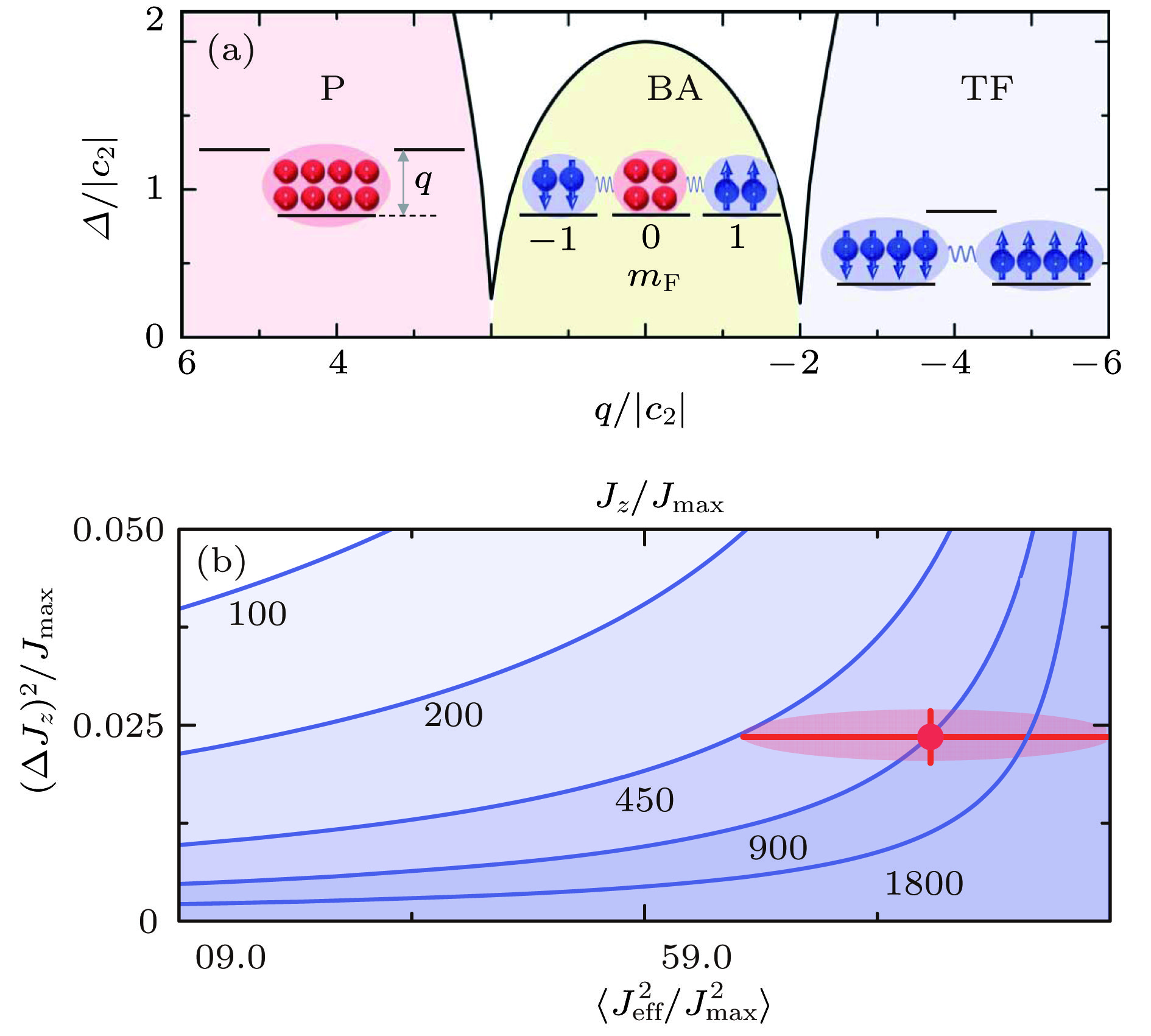
Figure 6. Useful $k$-particle entanglement for quantum metrology. $k$-separable states have a quantum Fisher information bounded by the solid line, Eq. (60). The dashed line is $F_{\rm Q}/N=k$. Here $N=100$. Adapted from Ref. [100].

DownLoad: Full-Size Img PowerPoint

图 7 (a) 量子相变产生双数态过程; (b) 纠缠宽度分析表明双数态纠缠宽度约为$910_{-450}^{+9900}$原子. 图取自文献[109]

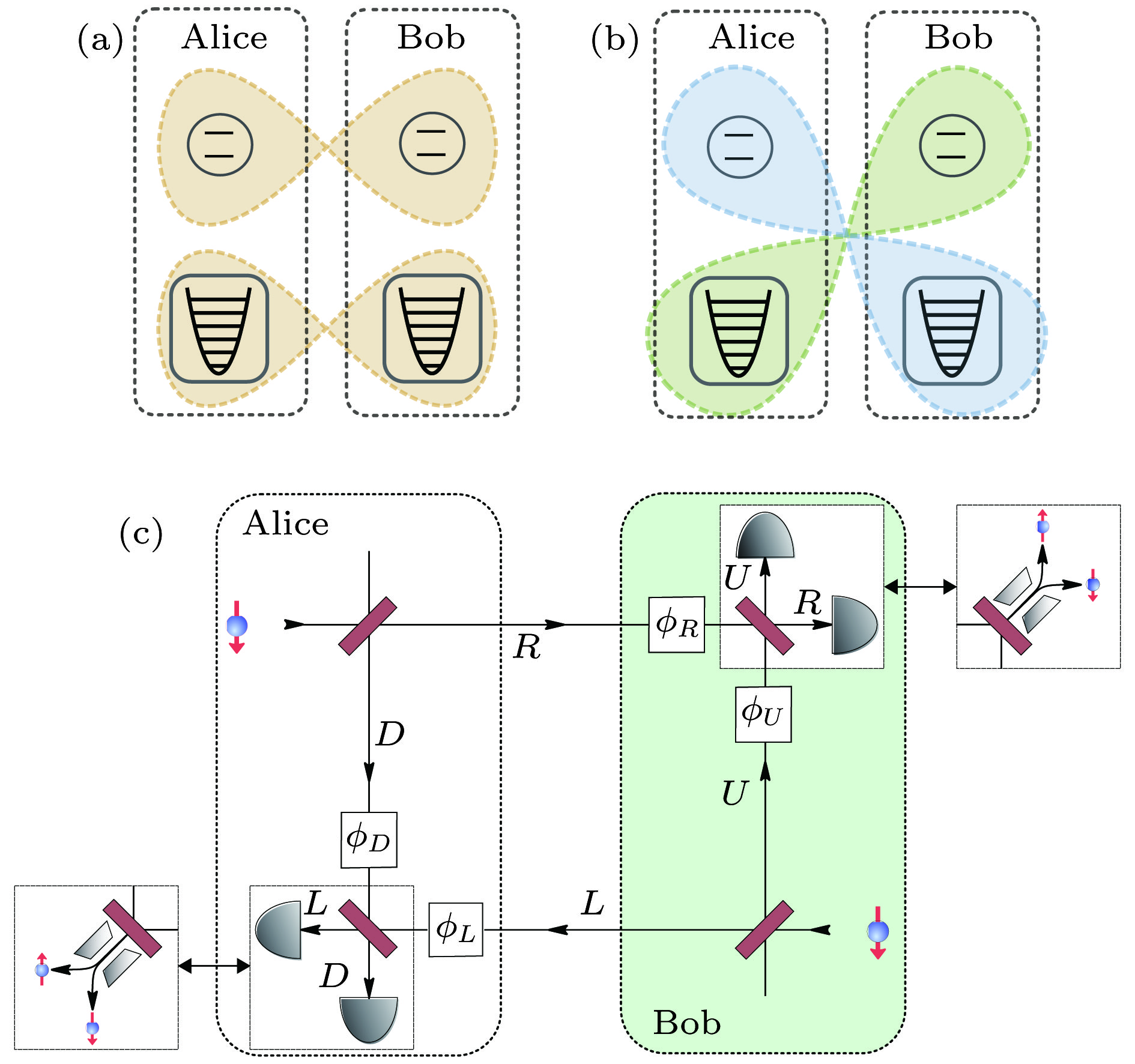
Figure 7. (a) Generation of twin-Fock state by quantum phase transition; (b) analysis of entanglement breadth for the Twin-Fock state samples, and it shows the entanglement breadth is at least $910_{-450}^{+9900}$ atoms. Adapted from Ref. [109].

DownLoad: Full-Size Img PowerPoint

图 8 两空间分离的粒子的相同自由度(a)和不同自由度(b)之间的非定域关联(Bell关联); (c)产生和验证自由度间非定域关联的实验方案. Alice 和 Bob 各自制备自旋态为 $\left\vert\downarrow\right\rangle$ 的原子并使其通过混合分束器. 分束器的两个输出分别与本地和对方的分析仪器相连. 第二个混合分束器作为各自的分析仪器的一部分, 将所得信号组合, 在两个粒子的不同自由度中产生了非定域关联. 通过CHSH不等式来区别, 此时两探测器的信号同时响应. 图取自文献[122]

Figure 8. (a) Hypernonlocality represents the simultaneous presence of Bell correlations among more than one DOF of two spatially separated particles; (b) hybrid nonlocality identifies Bell correlations among the discrete DOF of one particle and the continuous DOF of another distant particle; (c)experimental scheme for the generation and verification of inter-DOF entanglement. 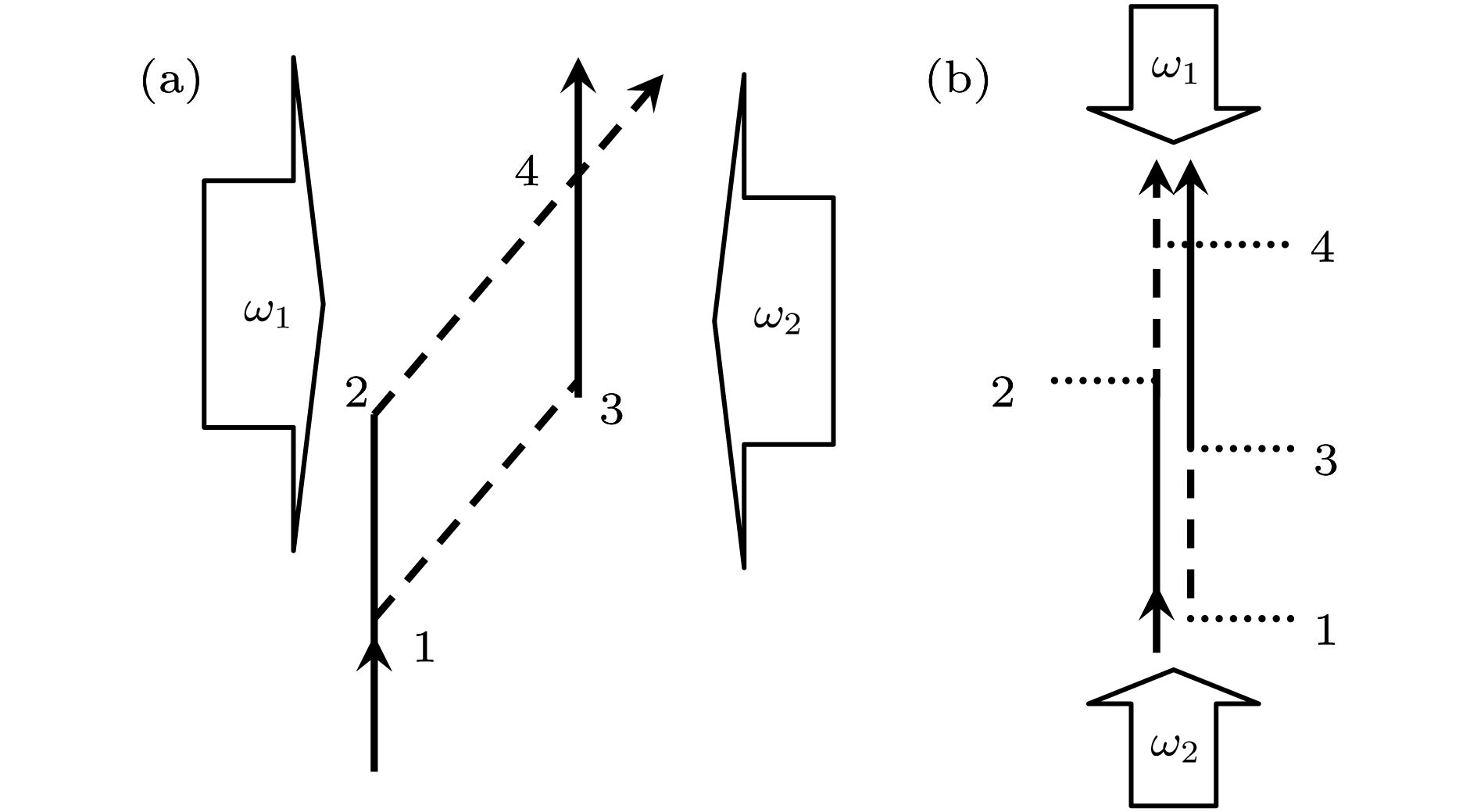Alice and Bob both prepare one particle in a spin-$\left\vert\downarrow\right\rangle$ state and submit it to a hybrid beam splitter. One of the output ports is sent to their local laboratory while the other is send to the opposite party. By mixing the local and the received copy using a second hybrid beam splitter, the desired correlations are established. Both parties now measure either spin or external d.o.f of their received particles, as depicted by the interchangeable measurement devices (white boxes). The recorded data from the events in which both parties receive exactly one particle violate a suitable CHSH inequality, independently of the measured DOF Adapted from Ref. [122].

DownLoad: Full-Size Img PowerPoint

图 9 广义Bloch球上马赫-曾德干涉仪和拉姆齐干涉仪对集体自旋的操作. 图取自文献[5]

Figure 9. Representation of Mach-Zehnder and Ramsey interferometer operations as rotations of the collective spin on the generalized Bloch sphere. Adapted from Ref. [5].

DownLoad: Full-Size Img PowerPoint

图 10 无量纲参数下的原子衍射图: KD衍射和Bragg衍射所满足的条件. 图取自文献[22]

Figure 10. Dimensionless parameter space for atom diffraction, KD labels curves corresponding to conditions that maximize Kapitza-Dirac diffraction, and Bragg indicates curves that correspond to conditions for Bragg reflection. Adapted from Ref. [22].

DownLoad: Full-Size Img PowerPoint

图 11 (a) 马赫-曾德原子干涉仪示意图; (b) 重力计原理示意图. 图取自文献[139]

Figure 11. (a) Schematic plot of Mach-Zehnder atom interferomery; (b) schematic plot of Gravimeter configuration. Adapted from Ref. [139].

DownLoad: Full-Size Img PowerPoint

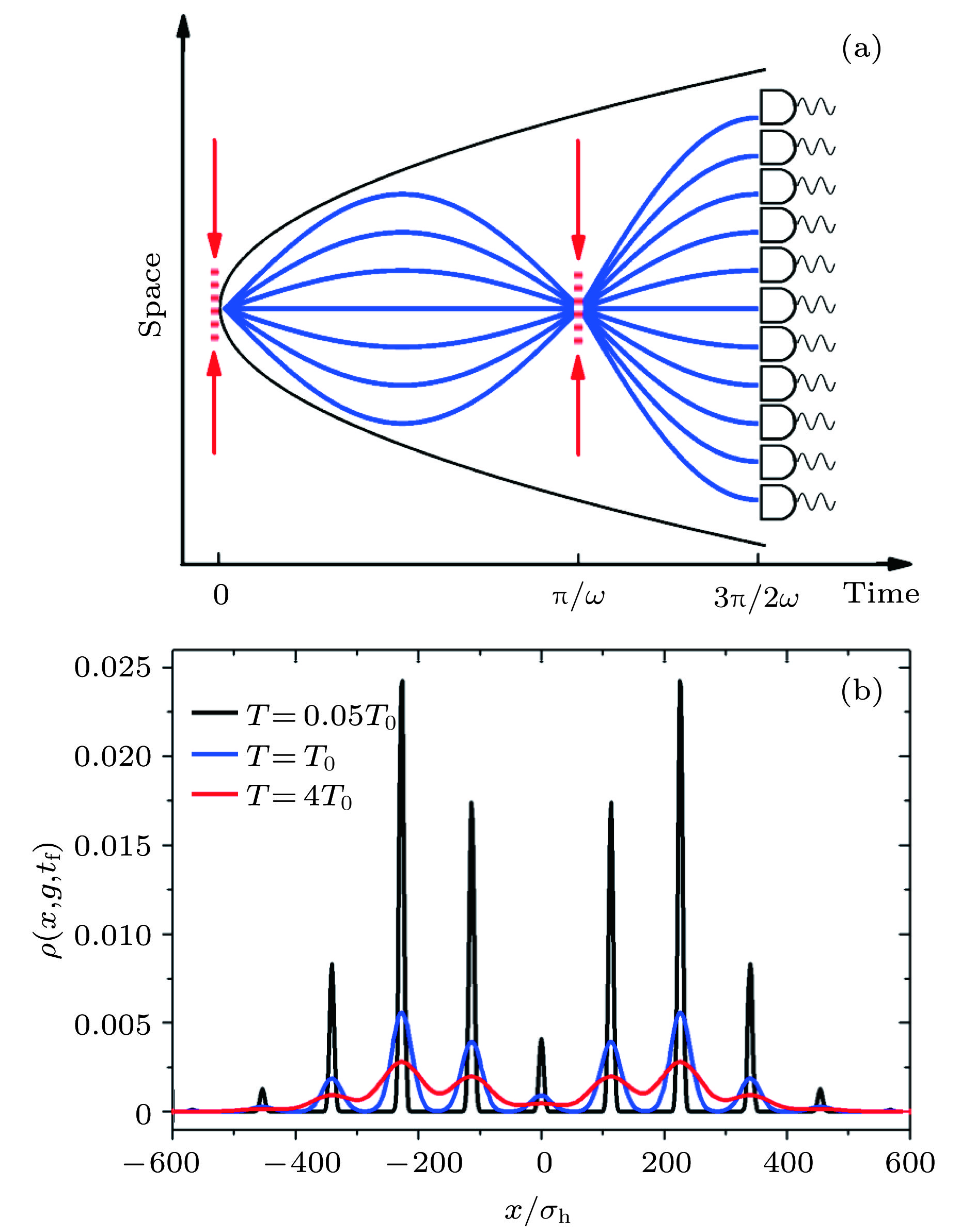
图 12 (a) 多模式KD 干涉仪. $t=0$时, 第一束KD脉冲将谐振势中原子复制多个原子波包. $t=\pi/\omega$时, 第二束KD脉冲对这些波包进行复合, 并在$t=3\pi/2\omega$时进行检测; (b) 测量时刻不同温度下原子的密度分布. 图取自文献[140]

Figure 12. (a) Multimodes Kapitza-Dirac interferometer. The first Kapitza-Dirac pulse at $t=0$ creates several modes consisting of atomic wave packets evolving under the harmonic confinement and an external perturbing field. The second Kapitza-Dirac pulse at $t=\pi/\omega$ mixes the modes which are eventually detected in output at $t=3\pi/2\omega$; (b) density profiles of the output wave function at temperatures below (dark line), equal (blue line), or above (red line) the crossover temperature $T_0$. Adapted from Ref. [140].

DownLoad: Full-Size Img PowerPoint

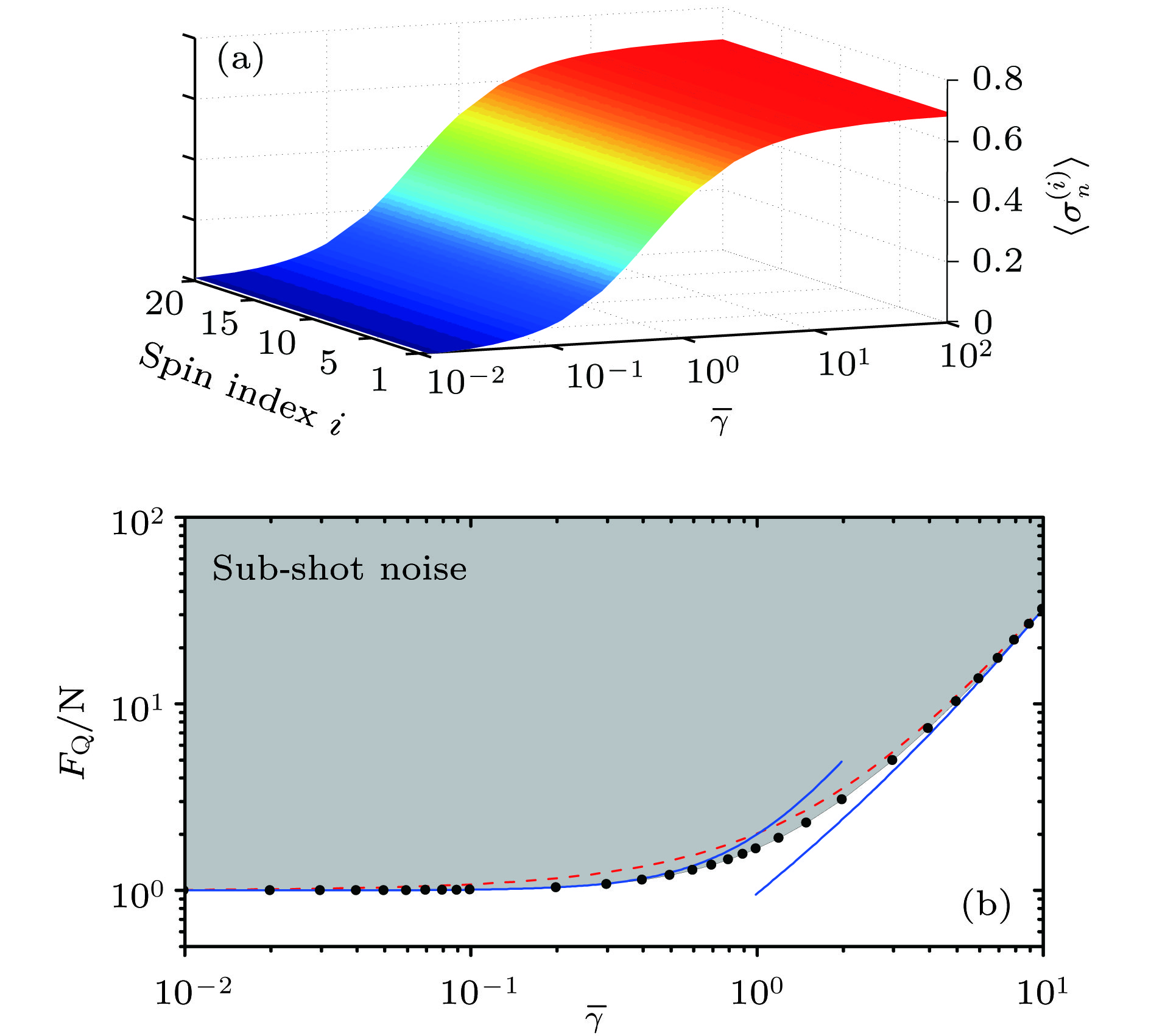
图 13 (a) 在Ising模型中, 平均自旋$\langle {\sigma}_{{n}}^{(i)}\rangle$随$\gamma$的变化情况; (b) $F_{\rm Q}/N$随$\gamma$的变化情况, 以及标准量子极限和亚散粒噪声极限的边界, 同时其也是判定有用量子纠缠态的边界[84]. 灰色区域为亚散粒噪声区域. 图取自文献[84]

Figure 13. we show the $\langle {\sigma} _{{n}}^{(i)}\rangle$ with respect to $\gamma$; (b) $F_{\rm Q}/N$ with respect to the $\gamma$ and give the boundary between standard quantum limit and sub-shot noise, which also witnesses the useful entanglement in Ref. [84]. The gray region denotes the sub-shot noise region. Adapted from Ref. [84].

DownLoad: Full-Size Img PowerPoint

图 14 (a) 在LMG模型中, 平均自旋$\langle {\sigma}_{{n}}^{(i)}\rangle$随$\gamma$的变化情况; (b) $F_Q/N$随$\gamma$的变化情况, 以及标准量子极限和亚散粒噪声极限的边界, 同时其也是判定有用量子纠缠态的边界[84]. 图取自文献[84]

Figure 14. (a) We show the $\langle \rm {\sigma} _{{n}}^{(i)}\rangle$ with respect to $\gamma$ in LMG model; (b) $F_{\rm Q}/N$ with respect to the $\gamma$ and give the boundary between standard quantum limit and sub-shot noise, which also witnesses the useful entanglement in Ref. [84]. The gray region denotes the sub-shot noise region. Adapted from Ref. [84].

DownLoad: Full-Size Img PowerPoint

图 15 (a) 最大似然估计偏差(绿色圆点)随独立测量次数$m$的变化, 误差为$(\Delta\theta_{\rm{MLE}})_{{\mu} \vert \theta_0}$; 红色曲线为$\pm \Delta \theta_{\rm CRB} = $$\pm |{\rm d} \langle \theta_{\rm MLE} \rangle_{{\mu} \vert \theta_0} / {\rm d}\theta_0|/\sqrt{mF(\theta_0)}$; (b) $ m F(\theta_0) (\varDelta^2\theta_{\rm{MLE}})_{{\mu} \vert \theta_0}$ (空心红圈)随$m$的变化. 红色实线为$({\rm d} \langle \theta_{\rm MLE} \rangle_{{\mu} \vert \theta_0} / {\rm d}\theta_0)^2$. 图取自文献[164]

Figure 15. (a) Bias $\langle \theta_{\rm MLE} \rangle_{{\mu} \vert \theta_0} - \theta_0$ (green dots) as function of $m$ with error bars $(\Delta\theta_{\rm{MLE}})_{{\mu} \vert \theta_0}$. The red lines are $\pm \Delta \theta_{\rm CRB} = $$\pm |{\rm d} \langle \theta_{\rm MLE} \rangle_{{\mu} \vert \theta_0} / {\rm d}\theta_0|/\sqrt{mF(\theta_0)}$; (b) variance of the maximum likelihood estimator multiplied by the Fisher information, $ m F(\theta_0) (\varDelta^2\theta_{\rm{MLE}})_{{\mu} \vert \theta_0}$ (red circles), as a function of the sample size $m$. It is compared to the bias $({\rm d} \langle \theta_{\rm MLE} \rangle_{{\mu} \vert \theta_0} / {\rm d}\theta_0)^2$ (red line). We recall that $\theta_0=\pi/4$ and $F(\theta_0)=4$ here. Adapted from Ref. [164].

DownLoad: Full-Size Img PowerPoint

图 16 不同先验概率下, 频率论方法得到相位估计值的方差($m (\varDelta^2 \theta_{\rm BL})_{{\mu} \vert \theta_0}$, 红色圆圈)及其边界CRB($m\varDelta^2 \theta_{\rm CRB}$, 红色虚线), 和贝叶斯相位估计的方差($m (\Delta^2 \theta_{\rm BL})_{{\mu},\theta \vert \theta_0}$, 蓝色圆圈)及其边界($m\varDelta^2 \theta_{\rm aGB}$, 蓝色实线)随样本$m$的变化 (a) $\alpha=-100$; (b) $\alpha=-10$; (c) $\alpha=1$; (d) $\alpha=10$. 每张图中内嵌的图是先验概率$p_{\rm pri}(\theta)$的分布图. 图取自文献[164]

Figure 16. Comparisons of phase estimation variance as a function of the sample size for Bayesian and frequentist data analysis under different prior distributions: (a) $\alpha=-100$; (b) $\alpha=-10$; (c) $\alpha=1$; (d) $\alpha=10$. In all figures, Red circles (frequentist) are $m (\varDelta^2 \theta_{\rm BL})_{{\mu} \vert \theta_0}$, the red dashed line is the CRB. $m\varDelta^2 \theta_{\rm CRB}$, Eq. (124). Blue circles (Bayesian) are $m (\varDelta^2 \theta_{\rm BL})_{{\mu},\theta \vert \theta_0}$, the blue solid line is the likelihood-averaged Ghosh bound $m\varDelta^2 \theta_{\rm aGB}$, Eq. (103). The inset in each panel is $p_{\rm pri}(\theta)$. Adapted from Ref. [164].

DownLoad: Full-Size Img PowerPoint

map

[1]	Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439 Google Scholar
[2]	Helstrom C W 1976 Quantum Detection and Estimation Theory (New York: Academic Press)
[3]	Giovannetti V S, Lioyd S, Maccone L 2006 Phys. Rev. Lett. 96 010401 Google Scholar
[4]	Pezzè L, Smerzi A 2014 Atom Interferometry, Proceedings of the International School of Physics, " Enrico Fermi” Course 188, Varenna, p691
[5]	Pezzè L, Smerzi A, Oberthaler M K, Schmied R, Treutlein P 2018 Rev. Mod. Phys. 90 035005 Google Scholar
[6]	Caves C M 1981 Phys. Rev. D 23 1693 Google Scholar
[7]	Wineland D J, Bollinger J J, Itano W M, Heinzen D J 1994 Phys. Rev. A 50 67 Google Scholar
[8]	Yurke B, McCall S L, Klauder J R 1986 Phys. Rev. A 33 4033 Google Scholar
[9]	Zou Y Q, Wu L N, Liu Q, Luo X Y, Guo S F, Cao J H, Tey M K, You L 2018 Proc. Natl. Acad. Sci. U.S.A. 115 6381 Google Scholar
[10]	Kruse I, Lange K, Peise J, Lücke B, Pezzè L, Arlt J, Ertmer W, Lisdat C, Santos L, Smerzi A, Klempt C 2016 Phys. Rev. Lett. 117 143004 Google Scholar
[11]	Muessel W, Strobel H, Linnemann D, Zibold T, Juliá-Dĺaz B, Oberthaler M K 2015 Phys. Rev. A 92 023603 Google Scholar
[12]	Muessel W, Strobel H, Linnemann D, Hume D B, Oberthaler M K 2014 Phys. Rev. Lett. 113 103004 Google Scholar
[13]	Strobel H, Muessel W, Linnemann D, Zibold T, Hume D B, Pezze L, Smerzi A, Oberthaler M K 2014 Science 345 424 Google Scholar
[14]	Ockeloen C F, Schmied R, Riedel M F, Treutlein P 2013 Phys. Rev. Lett. 111 143001 Google Scholar
[15]	Berrada T, Van Frank S, Bücker R, Schumm T, Schaff J F, Schmiedmayer J 2013 Nat. Commun. 4 2077 Google Scholar
[16]	Hamley C D, Gerving C S, Hoang T M, Bookjans E M, Chapman M S 2012 Nat. Phys. 8 305 Google Scholar
[17]	Lücke B, Scherer M, Kruse J, Pezzè L, Deuretzbacher F, Hyllus P, Topic O, Peise J, Ertmer W, Arlt J, Santos L, Smerzi A, Klempt C 2011 Science 334 773 Google Scholar
[18]	Riedel M F, Böhi P, Li Y, Hänsch T W, Sinatra A, Treutlein P 2010 Nature 464 1170 Google Scholar
[19]	Gross C, Zibold T, Nicklas E, Estève J, Oberthaler M K 2010 Nature 464 1165 Google Scholar
[20]	Estève J, Gross C, Weller A, Giovanazzi S, Oberthaler M K 2008 Nature 455 1216 Google Scholar
[21]	Giovannetti V, LIoyd S, Maccone L 2004 Science 306 1330 Google Scholar
[22]	Cronin A, Schmiedmayer J, Pritchard D E 2009 Rev. Mod. Phys. 81 1051 Google Scholar
[23]	Peters A, Chung K Y, Chu S 1999 Nature 400 849 Google Scholar
[24]	Peters A, Chung K Y, Chu S 2001 Metrologia 38 25 Google Scholar
[25]	Zhou L, Xiong Z Y, Yang W, Tang B A, Peng W C, Wang Y B, Xu P, Wang J, Zhan M S 2011 Chin. Phys. Lett. 28 013701 Google Scholar
[26]	Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 043610 Google Scholar
[27]	Gustavson T L, Bouyer P, Kasevich M A 1997 Phys. Rev. Lett. 78 2046 Google Scholar
[28]	Geiger R, Menort V, Stern G, Zahzam N, Cheinet P, Batelier B, Villing A, Moron F, Lours M, Bidel Y, Bresson A, Landragin A, Bouyer P 2011 Nat. Commun. 2 474 Google Scholar
[29]	Ekstrom C R, Schmiedmayer J, Chapman M S, Hammond T D, Pritchard D E 1995 Phys. Rev. A 51 3883 Google Scholar
[30]	Fixler J, Foster G, McGuirk J, Kasevich M A 2007 Science 315 74 Google Scholar
[31]	Lamporesi G, Bertoldi A, Cacciapuoti L, Prevedelli M, Tino G M 2008 Phys. Rev. Lett. 100 050801 Google Scholar
[32]	Bouchendira R, Clade P, Guellati-Khelifa S, Nez F, Biraben F 2011 Phys. Rev. Lett. 106 080801 Google Scholar
[33]	Rosi G, Sorrentino F, Cacciapuoti L, Prevedelli M, Tino G M 2014 Nature 510 518 Google Scholar
[34]	Parker R H, Yu C H, Zhong W C, Estey B, Müller H 2018 Science 360 191 Google Scholar
[35]	叶朝辉 2018 67 16 Ye Z H 2018 Acta Phys. Sin. 67 16
[36]	Ramesy N F 1949 Phys. Rev. 76 996
[37]	Ramesy N F 2005 Metrologia 42 S01
[38]	林弋戈, 方占军 2018 67 160604 Google Scholar Lin Y G, Fang Z J 2018 Acta Phys. Sin. 67 160604 Google Scholar
[39]	孙昌璞 2017 物理 46 481 Google Scholar Sun C P 2017 Physics 46 481 Google Scholar
[40]	Maxwell J C 1873 Treatise on Electricity and Magnetism (Oxford: Clarendon)
[41]	Ramesy N F 1956 Molecular Beams (Oxford: Oxford University Press)
[42]	Rabi I I 1937 Phys. Rev. 51 652 Google Scholar
[43]	Riehle F 2004 Frequency Standards: Basics and Applications (Wiley-VCH Verlag GmbH Co. KGaA)
[44]	管桦, 黄垚, 李承斌, 高克林 2018 67 164202 Google Scholar Guan H, Huang Y, Li C B, Gao K L 2018 Acta Phys. Sin. 67 164202 Google Scholar
[45]	Caves C M 1981 Phys. Rev. D 23 1693
[46]	Wineland D J, Bollinger J J, Itano W M, Morre F L, Heinzen D J 1992 Phys. Rev. A 46 R6797 Google Scholar
[47]	Pezzè L, Smerzi A 2009 Phys. Rev. Lett. 102 100401 Google Scholar
[48]	Toth G 2012 Phys. Rev. A 85 022322 Google Scholar
[49]	Braun D, Adesso G, Benatti F, Floreanini R, Marzolino U, Mitchell M W, Pirandola S 2018 Rev. Mod. Phys. 90 035006 Google Scholar
[50]	Zanardi P, Paris M G A, Venuti L C 2008 Phys. Rev. A 78 042105 Google Scholar
[51]	Invernizzi C, Korbman M, Venuti L C, Paris M G A 2008 Phys. Rev. A 78 042106 Google Scholar
[52]	Ma J, Wang X G 2009 Phys. Rev. A 80 012318 Google Scholar
[53]	Wang T L, Wu L N, Yang W, Jin G R, Lambert N, Nori F 2014 New J. Phys. 16 063039 Google Scholar
[54]	Gabbrielli M, Smerzi A, Pezzè L 2018 Sci. Rep. 8 15663 Google Scholar
[55]	Hauke P, Heyl M, Tagliacozzo L, Zoller P 2016 Nat. Phys. 12 778 Google Scholar
[56]	Pezzè L, Gabbrielli M, Lepori L, Smerzi A 2017 Phys. Rev. Lett. 119 250401 Google Scholar
[57]	Sun Z, Ma J, Lu X M, Wang X G 2010 Phys. Rev. A 82 022306 Google Scholar
[58]	Liu W F, Ma J, Wang X G 2013 J. Phys. A: Math. Theor. 46 045302 Google Scholar
[59]	Huang Y X, Zhong W, Sun Z, Wang X G 2012 Phys. Rev. A 86 012320 Google Scholar
[60]	Rao C R 1945 Bull. Calcutta Math. Soc. 37 81
[61]	Camer H 1946 Mathematical Methods of Statistics (Princeton: Princeton University Press)
[62]	Frechet M 1943 Rev. Internat. Stat. Inst. 11 182 Google Scholar
[63]	Darmoois G 1945 Rev. Internat. Stat. Inst. 13 9 Google Scholar
[64]	Fisher R A 1922 Proc. R. Soc. Edinburgh 42 321
[65]	Braunstein S L Caves C M, Milburn G J 1996 Ann. Phys. (N. Y.) 247 135 Google Scholar
[66]	Helstrom C W 1967 Phys. Lett. A 25 101 Google Scholar
[67]	Holevo A S 1982 Probabilistic and Statistical Aspects of Quantum Theory (Amsterdam: North-Holland)
[68]	Paris M G A 2009 Int. J. Quantum Inf. 7 125 Google Scholar
[69]	Wiseman H M, Milburn G J 2010 Quantum Measurement and Control (Cambridge: Combridge University Press)
[70]	Barndorff-Nielsen O E, Gill R D 2000 J. Phys. A 33 4481 Google Scholar
[71]	Zhong W, Huang Y X, Wang X G, Zhu S L 2017 Phys. Rev. A 95 052304 Google Scholar
[72]	Cohen M L 1968 IEEE Trans. Inf. Theory 14 591 Google Scholar
[73]	Liu J, Jing X X, Wang X G 2013 Phys. Rev. A 88 042316 Google Scholar
[74]	Zhang Y M, Li X W, Yang W, Jin G R 2013 Phys. Rev. A 88 043832 Google Scholar
[75]	Liu J, Jing X X, Zhong W, Wang X G 2014 Commun. Theor. Phys. 61 45 Google Scholar
[76]	Liu J, Chen j, Jing X X, Wang X G 2016 J. Phys. A 49 275302 Google Scholar
[77]	Pang S S, Brun T A 2014 Phys. Rev. A 90 022117 Google Scholar
[78]	Liu J, Jing X X, Wang X G 2015 Sci. Rep. 5 8565 Google Scholar
[79]	Zhong W, Sun Z, Ma J, Wang X G, Nori F 2013 Phys. Rev. A 87 022337 Google Scholar
[80]	Uys H, Meystre P 2007 Phys. Rev. A 76 013804 Google Scholar
[81]	Zhong W, Lu X M, Jing X X, Wang X G 2014 J. Phys. A: Math. Theor. 47 385304 Google Scholar
[82]	Gessner M, Pezze L, Smerzi A 2016 Phys. Rev. A 94 020101 Google Scholar
[83]	Wootters W K 1981 Phys. Rev. D 23 357 Google Scholar
[84]	Pezzè L, Li Yan, Li Weidong, Smerzi A 2016 Proc. Natl. Acad. Sci. U. S. A. 113 11459 Google Scholar
[85]	Braunstein S L, Lane A S, Caves C M 1992 Phys. Rev. Lett. 69 2153 Google Scholar
[86]	Li Y, Li W D 2018 Physica A 514 606
[87]	Liu J, Xiong H N, Song F, Wang X G 2014 Physica A 410 167 Google Scholar
[88]	Tommaso M, Augusto S, Luca P 2016 Phys. Rev. A 94 010102(R)Google Scholar
[89]	Wineland D J 2013 Rev. Mod. Phys. 85 1103 Google Scholar
[90]	Leibfried D, Blatt R, Monroe, Wineland D J 2003 Rev. Mod. Phys. 75 281 Google Scholar
[91]	Leibfried D, et. al. 2005 Nature 438 639 Google Scholar
[92]	Monz T, Schindler P, Barreiro J T, Chwalla M, Nigg D, Coish W, Harlander M H W, Hennrich M, Blatt R 2011 Phys. Rev. Lett. 106 130506 Google Scholar
[93]	Bollinger J J, Wayne M Itano, Wineland D J, Heinzen D J 1996 Phys. Rev. A 54 R4649 Google Scholar
[94]	Gerry C C, Mimih J 2010 Contemp. Phys. 51 497 Google Scholar
[95]	Leibfried D, et. al. 2004 Science 304 1476 Google Scholar
[96]	Walther P, et al. 2004 Nature 429 158 Google Scholar
[97]	Gao W B, et al. 2010 Nat. Phys. 6 331 Google Scholar
[98]	Wemer R F 1989 Phys. Rev. A 40 4277 Google Scholar
[99]	Gühne O, Tòth G 2009 Phys. Rep. 474 1 Google Scholar
[100]	Hyllus P, Laskowski W, Krischek R, Schwemmer C, Wieczorek W, Weinfurter H, Pezzè L, Smerzi A 2012 Phys. Rev. A 85 022321 Google Scholar
[101]	Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865 Google Scholar
[102]	Dur W, Vidal G, Cirac J I 2000 Phys. Rev. A 62 062314 Google Scholar
[103]	Gühne O, Tòth G, Briegel H J 2005 New. J. Phys. 7 229 Google Scholar
[104]	Sorensen A S, Kolmer K 2001 Phys. Rev. Lett. 86 4431 Google Scholar
[105]	Holland M J, Burnett 1993 Phys. Rev. Lett. 71 1355 Google Scholar
[106]	Lane A S, Braunstein S L, Caves C M 1993 Phys. Rev. A 47 1667 Google Scholar
[107]	Pezzè L, Smerzi A 2013 Phys. Rev. Lett. 110 163604 Google Scholar
[108]	Barreiro J T, et al. 2013 Nat. Phys. 9 559 Google Scholar
[109]	Luo X Y, Zou Y Q, Wu L N, Liu Q, Fan M F, Tey M K, You L 2017 Science 355 620 Google Scholar
[110]	Zeng Y, Xu P, He X, Liu Y Y, Liu M, Wang J, Papoular D J, Shlyapnikov G V, Zhan M S 2017 Phys. Rev. Lett. 119 160502 Google Scholar
[111]	Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
[112]	Amico L, Fazio R, Osterloh A, Vedral V 2008 Rev. Mod. Phys. 80 517 Google Scholar
[113]	Ma J, Wang X, Sun C P, Nori F 2011 Phys. Rep. 509 89 Google Scholar
[114]	Pan J W, Chen Z B, Lu C Y, Weinfurter H, Zeilinger A, Żukowski M 2012 Rev. Mod. Phys. 84 777 Google Scholar
[115]	Gühne O, Tòth G 2009 Phys. Rep. 474 1
[116]	Zhang Z, Duan L M 2013 Phys. Rev. Lett. 111 180401 Google Scholar
[117]	Zhang W, Zhou D L, Chang M S, Chapman M S, You L 2005 Phys. Rev. A 72 013602 Google Scholar
[118]	郑盟锟, 尤力 2018 67 160303 Google Scholar Tey M K, You L 2018 Acta Phys. Sin. 67 160303 Google Scholar
[119]	Feldmann P, Gessner M, Gabbrielli M, Klempt C, Santos L, Pezze L, Smerzi A 2018 Phys. Rev. A 97 032339 Google Scholar
[120]	Pezze L, Gessner M, Feldmann P, Klempt C, Santos L, Smerzi A 2017 arXiv: quant-ph 1712.03864v1
[121]	Brunner N, Cavalcanti D ironio S, Scarani V, Wehner S 2014 Rev. Mod. Phys. 86 419 Google Scholar
[122]	Li Y, Gessner M, Li Weidong, Smerzi A 2018 Phys. Rev. Lett. 120 050404 Google Scholar
[123]	Galitski V, Spielman I B 2013 Nature 494 49 Google Scholar
[124]	Zhai H 2015 Rep. Prog. Phys. 78 026001 Google Scholar
[125]	Yurke B 1986 Phys. Rev. Lett. 56 1515 Google Scholar
[126]	Zhou M, Duan X, Chen L, Luo Q, Xu Y, Hu Z 2015 Chin. Phys. B 24 050401 Google Scholar
[127]	Gabbrielli M, Pezzè L, Smerzi A 2015 Phys. Rev. Lett. 115 163002 Google Scholar
[128]	Moskowitz P, Gould P, Altas S, Pritchard D 1983 Phys. Rev. Lett. 51 370 Google Scholar
[129]	Ovchinikov Y B, Muller J H, Doery M R, Vredenbregt E J D, Helmerson K, Rolston S L, Phillips W D 1999 Phys. Rev. Lett. 83 284 Google Scholar
[130]	冯啸天, 袁春华, 陈丽清, 陈洁菲, 张可烨, 张卫平 2018 67 164204 Google Scholar Feng X T, Yuan C H, Chen L Q, Chen J F, Zhang K Y, Zhang W P 2018 Acta Phys. Sin. 67 164204 Google Scholar
[131]	Fray S, Diez C A, Hansch T W, Weitz M 2004 Phys. Rev. Lett. 93 240404 Google Scholar
[132]	Schlippert D, Hartwig J, Albers H, Richardson L L, Schubert C, Roura A, Schleich W P, Ertmer W, Rasel E M 2014 Phys. Rev. Lett. 112 203002 Google Scholar
[133]	Tarallo M G, Mazzoni T, Poli N, Sutyrin D V, Zhang X, Tino G M 2014 Phys. Rev. Lett. 113 023005 Google Scholar
[134]	Zhou L, Long S T, Tang B, Chen X, Gao F, Peng W C, Duan W T, Zhong J Q, Xiong Z Y, Wang J, Zhang Y Z, Zhan M S 2015 Phys. Rev. Lett. 115 013004 Google Scholar
[135]	Barrett B, Antoni-Micollier L, Chichet L, Battelier B, Leveque T, Landragin A, Bouyer P 2016 Nat. Commun. 7 13786 Google Scholar
[136]	Duan X C, Deng X B, Zhou M K, Zhang K, Xu W J, Xiong F, Xu Y Y, Shao C G, Luo J, Hu Z K 2016 Phys. Rev. Lett. 117 023001 Google Scholar
[137]	Rosi G, DAmico G, Cacciapuoti L, Sorrentino F, Prevedelli M, Zych M, Brukner Č, Tino G M 2017 Nat. Commun. 8 15529 Google Scholar
[138]	王谨, 詹明生 2018 67 160402 Google Scholar Wang J, Zhan M S 2018 Acta Phys. Sin. 67 160402 Google Scholar
[139]	Kasevich M, Chu S 1992 Appl. Phys. B 54 321 Google Scholar
[140]	Li W, He T, Smerzi A 2014 Phys. Rev. Lett. 113 023003 Google Scholar
[141]	Zernike F 1950 J. Opt. Soc. Am. 40 326 Google Scholar
[142]	D’Ariano G M, Paris M G A 1997 Phys. Rev. A 55 2267 Google Scholar
[143]	Chwedenczuk J, Piazza F, Smerzi A 2013 Phys. Rev. A 87 033607 Google Scholar
[144]	王倩, 魏荣, 王育竹 2018 67 163202 Google Scholar Wang Q, Wei R, Wang Y Z 2018 Acta Phys. Sin. 67 163202 Google Scholar
[145]	Cheng R, He T, Li W, Smerzi A 2016 J. Mod. Phys. 7 2043 Google Scholar
[146]	Ferrari G, Poli N, Sorrentino F, Tino G M 2006 Phys. Rev. Lett. 97 060402 Google Scholar
[147]	Luis A 2004 Phys. Lett. A 329 8 Google Scholar
[148]	Boixo S, Datta A, Flammia S T, Shaji A, Bagan E, Caves C M 2008 Phys. Rev. A 77 012317 Google Scholar
[149]	Boixo S, Datta A, Davis M J, Flammia S T, Shaji A, Caves C M 2008 Phys. Rev. Lett. 101 040403 Google Scholar
[150]	Woolley M J, Milburn G J, Caves C M 2008 New J. Phys. 10 125018 Google Scholar
[151]	Roy S M, Braunstein S L 2008 Phys. Rev. Lett. 100 220501 Google Scholar
[152]	Napolitano M, Mitchell M W 2010 New J. Phys. 12 093016 Google Scholar
[153]	Napolitano M, Koschorreck M, Dubost B, Behbood N, Sewell R J, Mitchell M W 2011 Nature 471 486 Google Scholar
[154]	Schaub P, et al. 2015 Science 347 1455 Google Scholar
[155]	Lipkin H J, Meshkov N, Glick A J 1965 Nucl. Phys. 62 188 Google Scholar
[156]	Meshkov N, Glick A J, Lipkin H J 1965 Nucl. Phys. 62 199 Google Scholar
[157]	Glick A J, Lipkin H J, Meshkov N 1965 Nucl. Phys. 62 211 Google Scholar
[158]	Dusuel S, Vidal J 2004 Phys. Rev. Lett. 93 237204 Google Scholar
[159]	Dusuel S, Vidal J 2005 Phys. Rev. B 71 224420 Google Scholar
[160]	Wichterich H, Vidal J, Bose S 2010 Phys. Rev. A 81 032311 Google Scholar
[161]	Ma J, Wang X 2009 Phys. Rev. A 80 012318
[162]	Salvatori G, Mandarino A, Paris M G A 2014 Phys. Rev. A 90 022111 Google Scholar
[163]	VanTrees H L, Bell K L, Tian Z 2013 Detection, Estimation and modulation theory (WILEYINTERSCIENCE A JOHN WILEY and SONS, INC., PUBLICATION)
[164]	Li Y, Pezzè L, Gessner M, Ren Z H, Li W D, Smerzi A 2018 Entropy 20 628 Google Scholar
[165]	Hayashi M 2005 Asymptotic Theory of Quantum Statistical Inference, Selected Papers (Singapore:World Scientific Publishing)
[166]	Lehmann E L, Casella G 1998 Theory of Point Estimation (Berlin: Springer）
[167]	Barankin E W 1949 Ann. Math. Stat. 20 477 Google Scholar
[168]	Mcaulay R J, Hofstetter E M 1971 IEEE Trans. Inf. Theory 17 669 Google Scholar
[169]	Hammersley J M 1950 J. Roy. Statist. Soc. Ser. B 12 192
[170]	Chapman D G, Robbins H 1951 Ann. Math. Statist. 22 581 Google Scholar
[171]	Sivia D S, Skilling J 2006 Data Analysis: A Bayesian Tutorial (London: Oxford University Press)
[172]	Ghosh M 1993 Stat. Prob. Lett. 17 173 Google Scholar
[173]	Kay S M 1993 Fundamentals of Statistical Signal Processing: Estimation Theory(Volume I) (New Jersey: Prentice Hall)
[174]	Gessner M, Pezzè , Smerzi A 2016 Phys. Rev. A 94 020101
[175]	Gessner M, Pezze L, Smerzi A 2017 Quantum 1 17 Google Scholar
[176]	Qin Z Z, Gessner M, Ren Z H, Deng X, Han D, Li W D, Su X L, Smerzi A, Peng K C 2019 npj Quantum Inf. 5 3 Google Scholar
[177]	Suzuki J 2016 J. Math. Phys. 57 042201 Google Scholar
[178]	Pezzè L, Ciampini M A, Spagnolo N, Humphreys P C, Datta A, Walmsley I A, Barbieri M, Sciarrino F, Smerzi A 2017 Phys. Rev. Lett. 119 130504 Google Scholar
[179]	Gessner M, Pezze L, Smerzi A 2018 Phys. Rev. Lett. 121 130503 Google Scholar
[180]	Zhuang M, Huang J, Lee C H 2018 Phys. Rev. A 98 033603 Google Scholar
[181]	Tsang M, Wiseman H M, Caves C M 2011 Phys. Rev. Lett. 106 090401 Google Scholar
[182]	Liu J, Yuan H D 2016 New J. Phys. 18 093009 Google Scholar
[183]	Tsang M 2012 Phys. Rev. Lett. 108 230401 Google Scholar
[184]	Lu X M, Tsang M 2016 Quantum Sci. Technol. 1 015002 Google Scholar

[1]	Ren Ya-Lei, Zhou Tao. Quantum Fisher information in moving reference frame. Acta Physica Sinica, 2024, 73(5): 050601. doi: 10.7498/aps.73.20231394
[2]	Bai Jian-Nan, Han Song, Chen Jian-Di, Han Hai-Yan, Yan Dong. Correlated collective excitation and quantum entanglement between two Rydberg superatoms in steady state. Acta Physica Sinica, 2023, 72(12): 124202. doi: 10.7498/aps.72.20222030
[3]	Li Jing, Ding Hai-Tao, Zhang Dan-Wei. Quantum Fisher information and parameter estimation in non-Hermitian Hamiltonians. Acta Physica Sinica, 2023, 72(20): 200601. doi: 10.7498/aps.72.20230862
[4]	Liu Ran, Wu Ze, Li Yu-Chen, Chen Yu-Quan, Peng Xin-Hua. Experimentally characterizing multiparticle entanglement based on measuring quantum Fisher information. Acta Physica Sinica, 2023, 72(11): 110305. doi: 10.7498/aps.72.20230356
[5]	Li Yan, Ren Zhi-Hong. Quantum Fisher information of multi-qubit WV entangled state under Lipkin-Meshkov-Glick model. Acta Physica Sinica, 2023, 72(22): 220302. doi: 10.7498/aps.72.20231179
[6]	Niu Ming-Li, Wang Yue-Ming, Li Zhi-Jian. Estimation of light-matter coupling constant under dispersive interaction based on quantum Fisher information. Acta Physica Sinica, 2022, 71(9): 090601. doi: 10.7498/aps.71.20212029
[7]	Xu Peng, He Xiao-Dong, Liu Min, Wang Jin, Zhan Ming-Sheng. Experimental progress of quantum computation based on trapped single neutral atoms. Acta Physica Sinica, 2019, 68(3): 030305. doi: 10.7498/aps.68.20182133
[8]	Zhao Jun-Long, Zhang Yi-Dan, Yang Ming. Influence of noice on tripartite quantum probe state. Acta Physica Sinica, 2018, 67(14): 140302. doi: 10.7498/aps.67.20180040
[9]	Wu Ying, Li Jin-Fang, Liu Jin-Ming. Enhancement of quantum Fisher information of quantum teleportation by optimizing partial measurements. Acta Physica Sinica, 2018, 67(14): 140304. doi: 10.7498/aps.67.20180330
[10]	Tey Meng-Khoon, You Li. Generation of twin-Fock states for precision measurement beyond the standard quantum limit. Acta Physica Sinica, 2018, 67(16): 160303. doi: 10.7498/aps.67.20181029
[11]	Guo Hong. Effects of initial states on the quantum correlation in Bose-Hubbard model. Acta Physica Sinica, 2015, 64(22): 220301. doi: 10.7498/aps.64.220301
[12]	Chang Feng, Wang Xiao-Qian, Gai Yong-Jie, Yan Dong, Song Li-Jun. Quantum Fisher information and spin squeezing in the interaction system of light and matter. Acta Physica Sinica, 2014, 63(17): 170302. doi: 10.7498/aps.63.170302
[13]	He Zhi, Li Long-Wu. Quantum correlation dynamics of two two-level atoms in common environment. Acta Physica Sinica, 2013, 62(18): 180301. doi: 10.7498/aps.62.180301
[14]	Zhao Jian-Hui, Wang Hai-Tao. Quantum phase transition and ground state entanglement of the quantum spin system: a MERA study. Acta Physica Sinica, 2012, 61(21): 210502. doi: 10.7498/aps.61.210502
[15]	Song Li-Jun, Yan Dong, Liu Yie. Quantum Fisher information and chaos in the system of Bose-Einstein condensate. Acta Physica Sinica, 2011, 60(12): 120302. doi: 10.7498/aps.60.120302
[16]	Zhou Nan-Run, Zeng Bin-Yang, Wang Li-Jun, Gong Li-Hua. Selective automatic repeat quantum synchronous communication protocol based on quantum entanglement. Acta Physica Sinica, 2010, 59(4): 2193-2199. doi: 10.7498/aps.59.2193
[17]	Chen Yu, Zou Jian, Li Jun-Gang, Shao Bin. Controlling the entanglement among three atoms by quantum-jump-based feedback. Acta Physica Sinica, 2010, 59(12): 8365-8370. doi: 10.7498/aps.59.8365
[18]	Hu Yao-Hua, Fang Mao-Fa, Liao Xiang-Ping, Zheng Xiao-Juan. Quantum entanglement of the binomial field interacting with a cascade three-level atom. Acta Physica Sinica, 2006, 55(9): 4631-4637. doi: 10.7498/aps.55.4631
[19]	Wang Cheng-Zhi, Fang Miao-Fa. . Acta Physica Sinica, 2002, 51(9): 1989-1995. doi: 10.7498/aps.51.1989
[20]	Xiong Jin, Niu Zhong-Qi, Zhang Zhi-Ming. . Acta Physica Sinica, 2002, 51(10): 2245-2244. doi: 10.7498/aps.51.2245

Catalog

Vol. 68, Issue 4 - 2019-02-20

Metrics

Abstract views: 22187
PDF Downloads: 708
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板