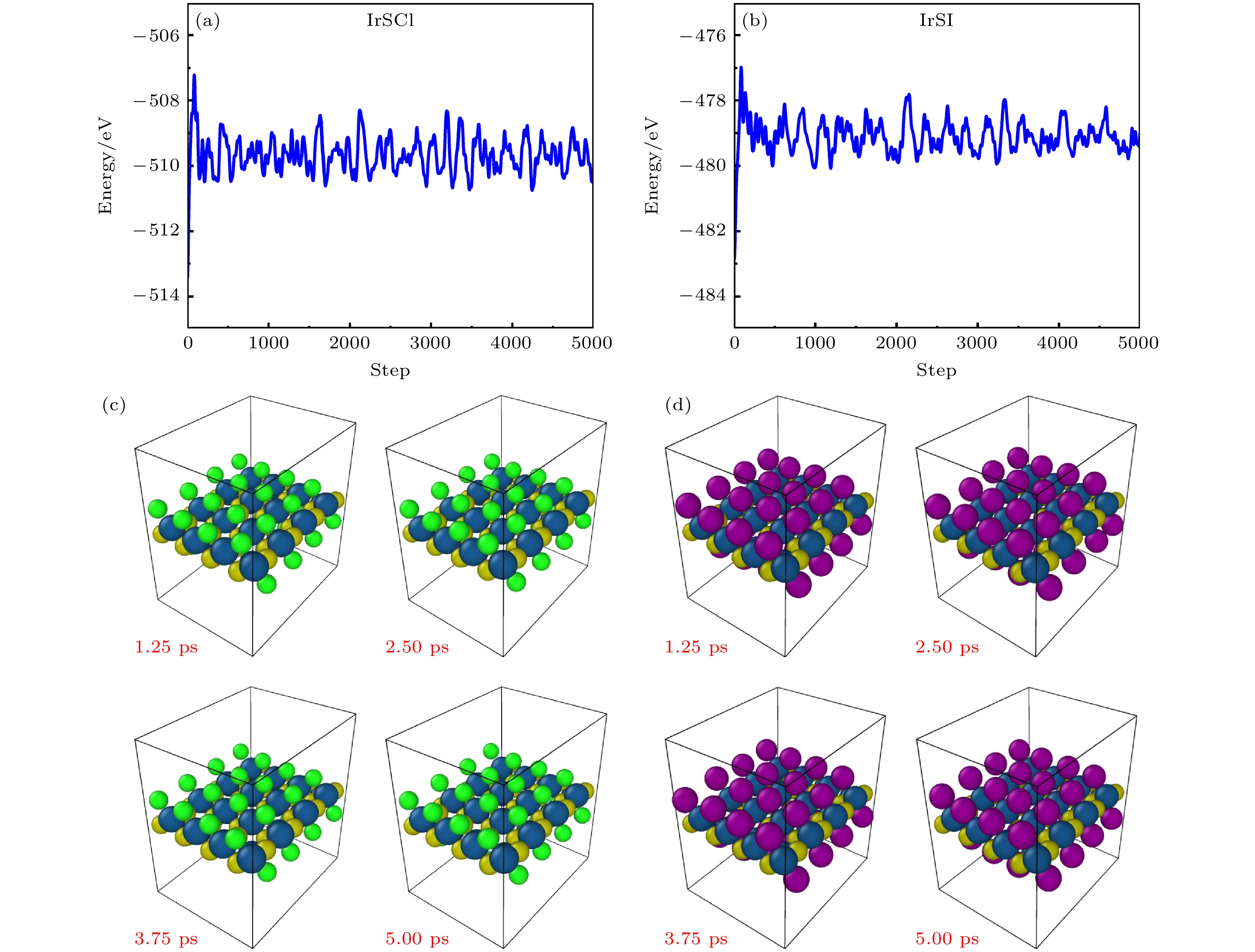
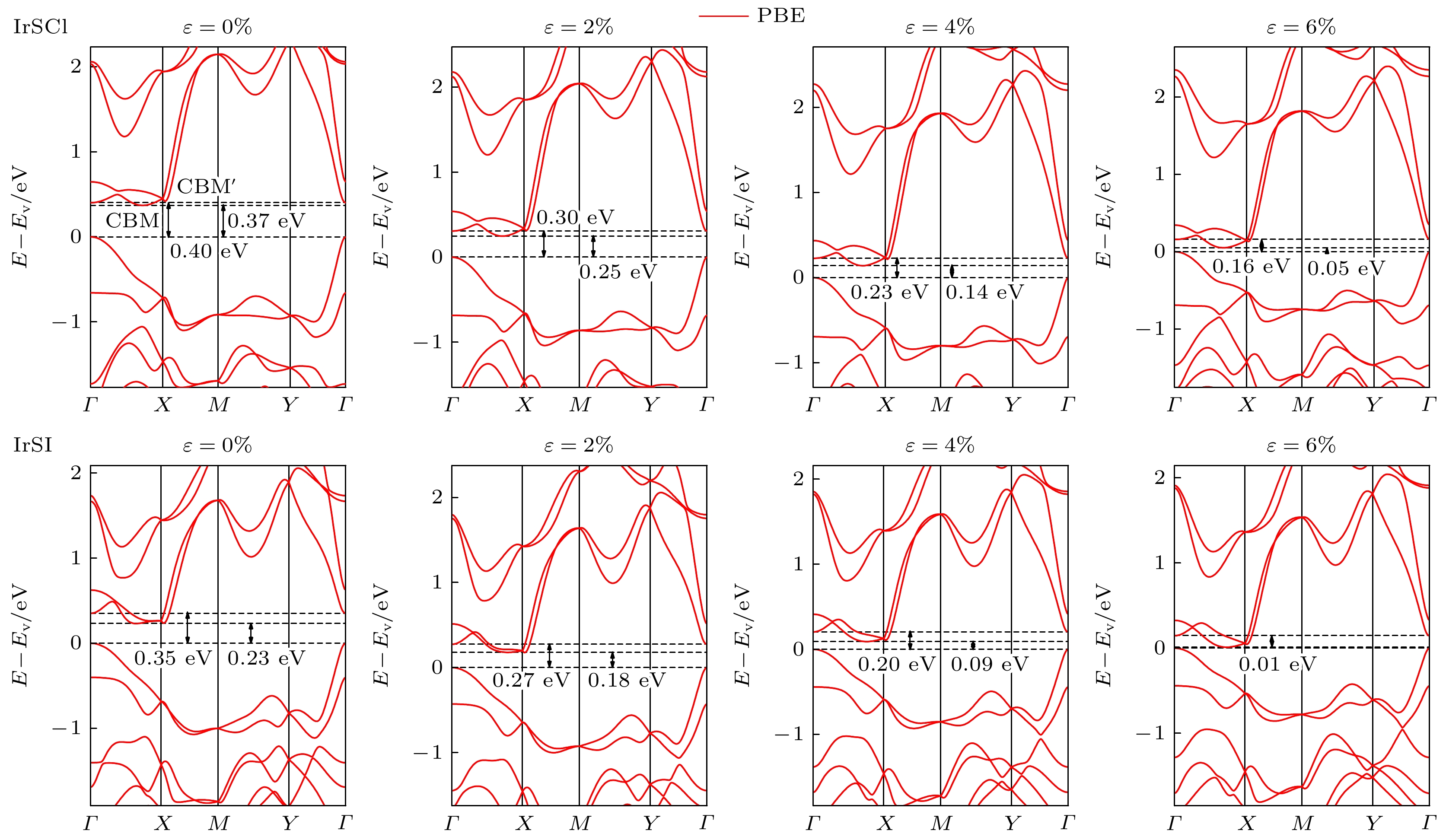
-
基于密度泛函理论的第一性原理计算方法, 系统研究了单层IrSCl和IrSI材料的载流子输运特性. 声子谱计算无虚频, 表明材料结构稳定, 且分子动力学模拟验证了其在300 K下的热稳定性. 结果显示, 这两种材料均为间接带隙半导体, 且在不同泛函下的带隙计算结果分别为: 单层IrSCl在PBE和HSE06泛函下的带隙.为0.37 eV和1.58 eV, 单层IrSI的带隙为0.23 eV和1.36 eV. 在双轴拉伸应变下, IrSCl和IrSI的带隙逐渐减小. 在应变6%时, 带隙分别降至0.05 eV和0.01 eV (PBE). 基于形变势理论预测, 室温下单层IrSCl和IrSI的最大载流子迁移率分别407.77 cm2/(V·s)和202.64 cm2/(V·s). 同时, 基于玻尔兹曼输运方程的计算结果显示, 室温下单层IrSCl和IrSI的载流子迁移率最大值分别299.15 cm2/(V·s)和286.41 cm2/(V·s). 这些结果表明, IrSCl和IrSI单层材料在纳米电子器件领域具有潜在的应用价值.Carrier mobility is a key parameter determining the response speed of charge carriers to electric fields in nanoelectronic devices. This study aims to investigate the charge carrier transport properties of monolayer IrSCl and IrSI. Using first-principles calculations based on density functional theory, we systematically investigate the electronic structure and transport properties of monolayer IrSCl and IrSI. The phonon dispersion calculations indicate that both IrSCl and IrSI exhibit no imaginary frequencies, confirming their structural stability. Furthermore, molecular dynamics simulations demonstrate that these materials maintain thermal stability at room temperature (300 K). The evaluation of the bandgap by using the Perdew-Burke-Ernzerhof (PBE) functional and the hybrid HSE06 functional shows that both IrSCl and IrSI are indirect bandgap semiconductors. The bandgap values for monolayer IrSCl are 0.37 eV and 1.58 eV under the PBE functional and the HSE06 functional, respectively, while those for monolayer IrSI are 0.23 eV and 1.36 eV under the PBE functional and the HSE06 functional, respectively. We further investigate the effects of biaxial tensile strain on the bandgap. The bandgap of IrSCl and IrSI decrease with the increase of strain, respectively reaching 0.05 eV and 0.01 eV under the PBE functional at a strain of 6%, indicating a strain-induced transition to metallic behavior. According to deformation potential theory and the Boltzmann transport equation, we calculate the carrier mobility for each of monolayer IrSCl and IrSI. The predicted maximum carrier mobility at room temperature is 407.77 cm2/(V·s) for monolayer IrSCl, and 202.64 cm2/(V·s) for monolayer IrSI. Additionally, the results from the Boltzmann transport equation show that the highest mobility is 299.15 cm2/(V·s) for IrSCl and 286.41 cm2/(V·s) for IrSI. These findings suggest that both IrSCl and IrSI possess favorable electronic and transport properties, thus they have become promising candidates for future applications in the field of two-dimensional nanoelectronic devices. Notably, the combination of a moderate bandgap and high carrier mobility at room temperature indicates their potential applications in the fields of transistors, sensors, and other electronic components. This study provides valuable insights into the material properties of IrSCl and IrSI, contributing to the design of novel two-dimensional materials for electronic applications.
-
Keywords:
- first-principles calculation /
- mobility /
- two-dimensional materials
[1] Feng L P, Li A, Wang P C, Liu Z T 2018 J. Phys. Chem. C 42 122
Google Scholar
[2] Su Y, Cao S, Shi L B, Qian P 2020 Appl. Surf. Sci. 531 147341
Google Scholar
[3] Qu H Z, Zhang S L, Zhou W H, Guo S Y, Zeng H B 2020 IEEE Electron Device Lett. 41 1029
Google Scholar
[4] Li Q, Du B D, Gao J Y, Liu J 2023 Appl. Phys. Rev. 10 011402
Google Scholar
[5] Guo S Y, Wang Y, Qu H Z, Zhou W H, Ang Y S, Zhang S L, Zeng H B 2024 Phys. Rev. Appl. 21 054016
Google Scholar
[6] Shi H, Yang S Y, Wang H P, Ding D P, Hu Y, Qu H Z, Chen C Y, Hu X M, Zhang S L 2024 ACS Appl. Mater. Interfaces 16 39592
Google Scholar
[7] Song Y, Pan J B, Zhang Y F, Yang H T, Du S X 2021 J. Phys. Chem. Lett. 12 6007
Google Scholar
[8] Whitfield G, Shaw P B 1980 Phys. Rev. B 21 4349
Google Scholar
[9] Zunger A 2019 Nature 566 447
Google Scholar
[10] Göser O, Paul W, Kahle H G 1990 J. Magn. Magn. Mater. 92 129
Google Scholar
[11] Fei R X, Yang L 2014 Nano Lett. 14 2884
Google Scholar
[12] Qiao J S, Kong X H, Hu Z X, Yang F, Ji W 2014 Nat. Commun. 5 4475
Google Scholar
[13] Lang H F, Zhang S Q, Liu Z R 2016 Phys. Rev. B 94 235306
Google Scholar
[14] Generazio E R, Spector H N 1979 Phys. Rev. B 20 5162
Google Scholar
[15] Shi L B, Zhang Y Y, Xiu X M, Dong H K 2018 Carbon 134 103
Google Scholar
[16] Zhang Y J, Cao S, Wang Y Z, Jian X D, Shi L B, Qian P 2021 Phys. Lett. A 401 127340
Google Scholar
[17] Poncé S, Jena D, Giustino F 2019 Phys. Rev. B 100 085204
Google Scholar
[18] Poncé S, Jena D, Giustino F 2019 Phys. Rev. Lett. 123 096602
Google Scholar
[19] Poncé S, Li W, Reichardt S, Giustino F 2020 Rep. Prog. Phys. 83 036501
Google Scholar
[20] Alidoosty-Shahraki M, Bashirpour M 2020 IEEE Trans. Electron Devices 67 3459
Google Scholar
[21] Shi L B, Cao S, Yang M, You Q, Zhang K C, Bao Y, Zhang Y J, Niu Y Y, Qian P 2019 J. Phys.: Condens. Matter 32 065306
Google Scholar
[22] Su Y, Li N, Shi L B, Wang L Z, Qian P 2022 Comput. Mater. Sci. 213 111609
Google Scholar
[23] 王晓艳, 张鹤鸣, 宋建军, 马建立, 王冠宇, 安久华 2011 60 077205
Google Scholar
Wang X Y, Zhang H M, Song J J, Ma J L, Wang G Y, An J H 2011 Acta Phys. Sin. 60 077205
Google Scholar
[24] Hamann D, Schlüter M, Chiang C 1979 Phys. Rev. Lett. 43 1494
Google Scholar
[25] Perdew J, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[26] Baroni S, Giannozzi P 2009 AGU Fall Meet. Abstr. 21 395502
Google Scholar
[27] Itvinov I V 2006 Appl. Phys. Lett. 89 43
Google Scholar
[28] Noffsinger J, Giustino F, Malone B D, Park C H, Louie S G, Cohen M L 2010 Comput. Phys. Commun. 181 2140
Google Scholar
-
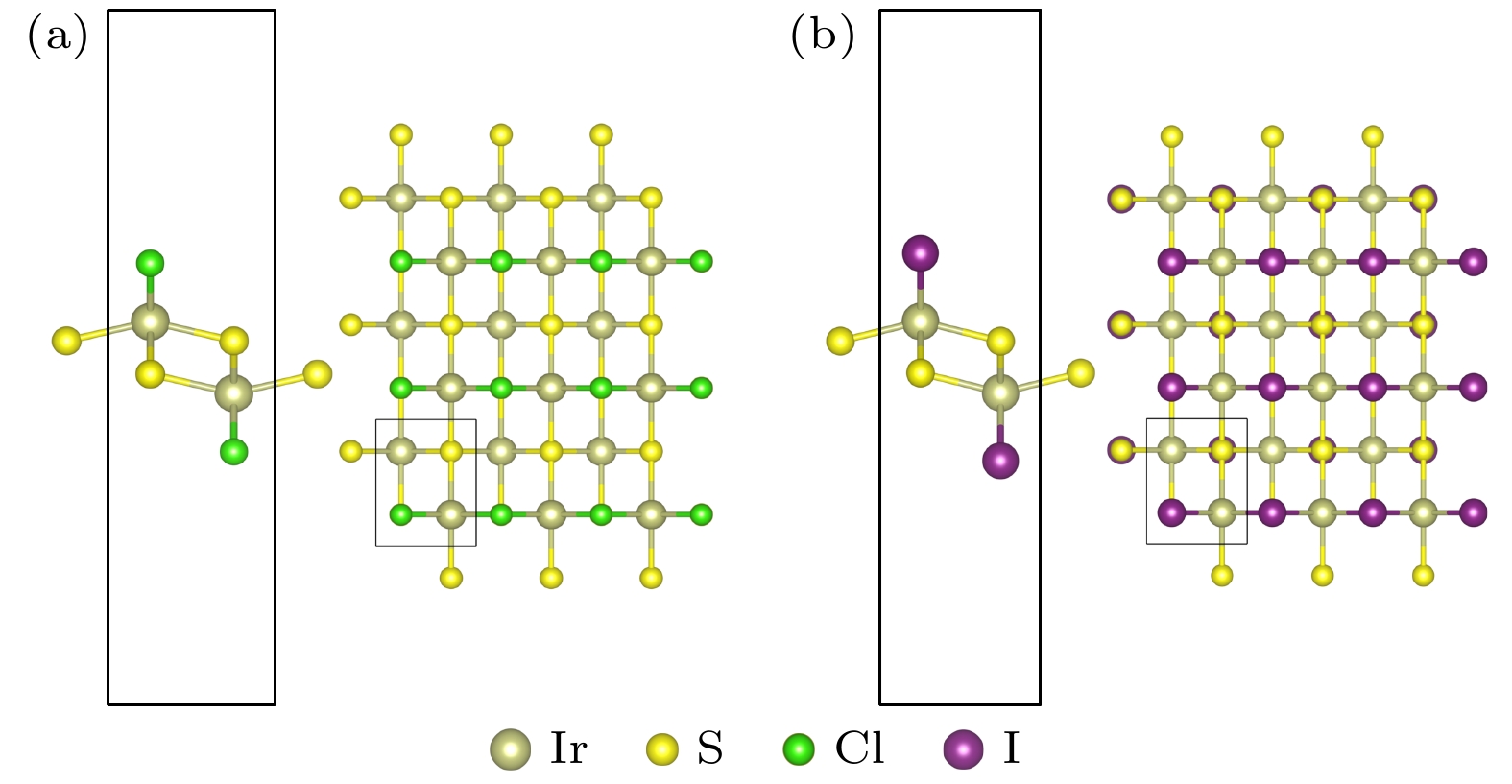
图 1 (a)单层IrSCl的晶胞结构. 其中黄色原子表示S, 金黄色原子表示Ir, 绿色原子表示Cl; (b)单层IrSI的晶胞结构, 在该结构中, 黄色原子同样表示S, 金黄色原子同样表示Ir, 紫色原子表示I. 将水平方向定义为x轴正方向, 垂直方向定义为y轴正方向
Fig. 1. (a) Unit cell structure of monolayer IrSCl, where the yellow atoms denote sulfur (S), the golden yellow atoms denote iridium (Ir), and the green atoms denote chlorine (Cl); (b) the unit cell structure of monolayer IrSI, with the yellow atoms again representing sulfur (S), the golden yellow atoms representing iridium (Ir), and the purple atoms representing iodine (I). In both figures, the horizontal direction is defined as the positive x-axis, and the vertical direction is defined as the positive y-axis.
图 2 (a) IrSCl的AIMD结果; (b) IrSI的AIMD结果; (c), (d) IrSCl和IrSI在第1.25, 2.50, 3.75和5.00 ps时的结构状态
Fig. 2. (a) The AIMD results for IrSCl; (b) the AIMD results for IrSI; (c), (d) the structural states of IrSCl and IrSI at 1.25, 2.50, 3.75 and 5.00 ps.
图 3 双轴拉伸下的能带结构图, 其中上面四幅图为IrSCl, 下边四幅图为IrSI, 应变范围为0%—10%, 间隔为2%
Fig. 3. Band structure under biaxial tensile strain. The top four panels are for IrSCl, and the bottom four panels are for IrSI, with strain ranging from 0% to 10% in 2% intervals.
图 4 基于HSE06泛函计算的IrSCl和IrSI能带图 (a) IrSCl; (b) IrSI
Fig. 4. Band structure of IrSCl and IrSI based on HSE06 functional calculations: (a) IrSCl; (b) IrSI.
图 5 IrSCl和IrSI形变势和弹性模量拟合
Fig. 5. Fitting of deformation potential (DPT) and elastic modulus for IrSCl and IrSI.
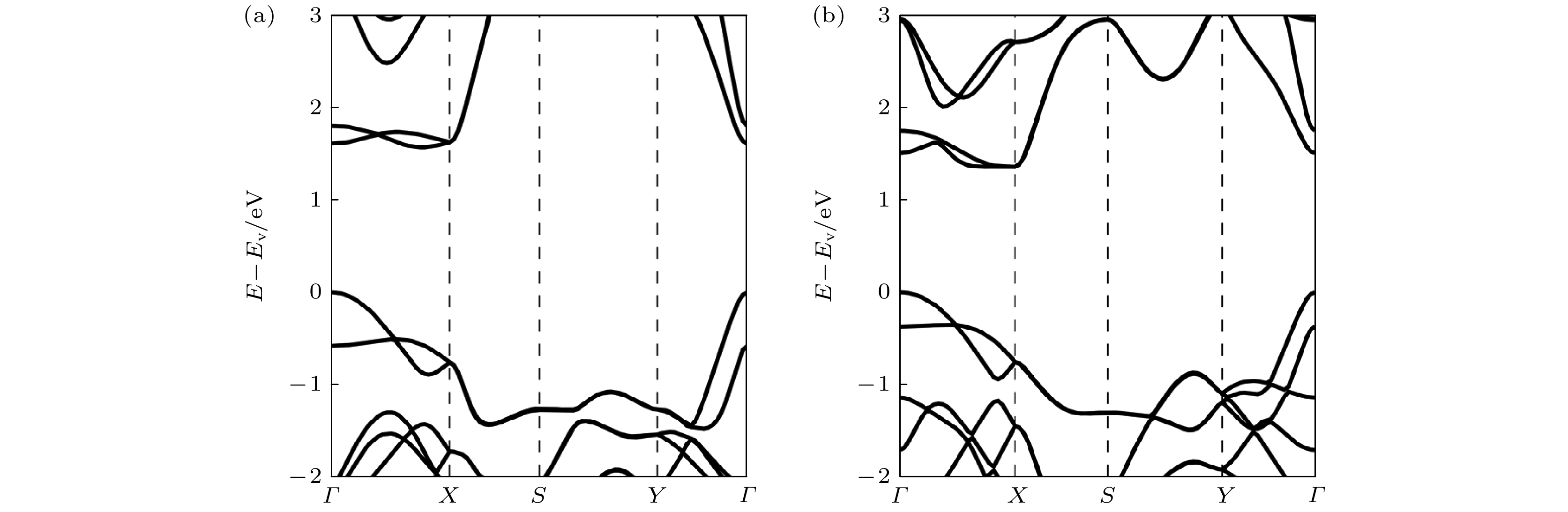
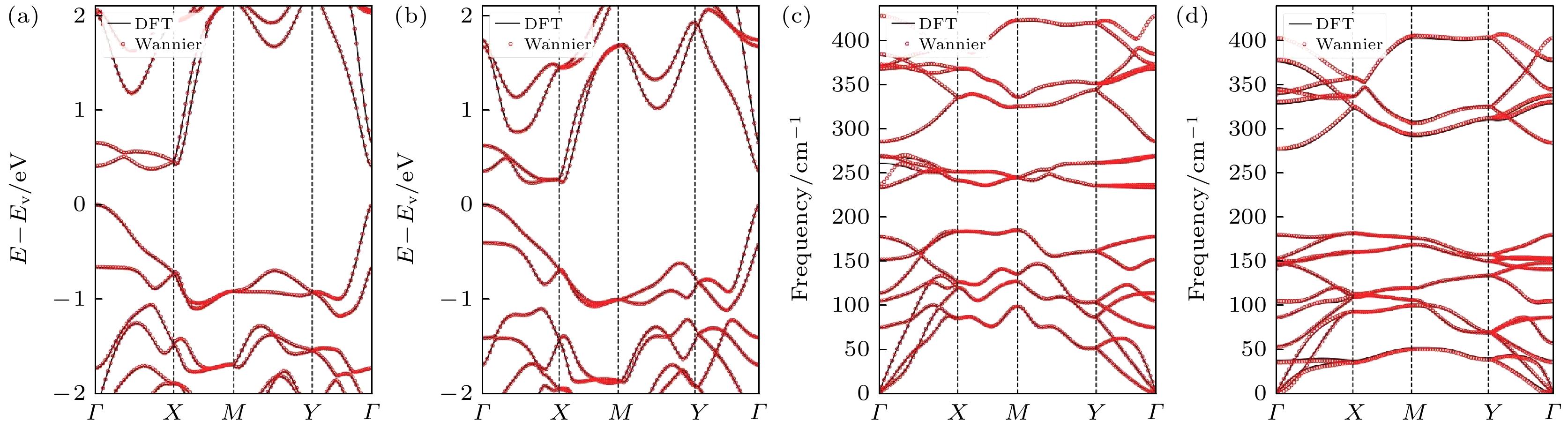
图 6 (a) IrSCl能带插值前后对比; (b) IrSI能带插值前后对比; (c)声子谱IrSCl插值前后对比; (d) IrSI声子谱插值前后对比
Fig. 6. (a) Comparison before and after band interpolation of IrSCl; (b) comparison before and after band interpolation of IrSI; (c) comparison before and after phonon spectrum interpolation of IrSCl; (d) comparison before and after phonon spectrum interpolation of IrSI
图 7 (a) Wannier插值深度测试; (b) Wannier插值密度测试
Fig. 7. (a) Testing the depth of Wannier function interpolation; (b) testing the density of Wannier function interpolation.
图 8 基于玻尔兹曼输运方程计算得到的不同温度下单层IrSCl和IrSI的载流子迁移率
Fig. 8. Calculated temperature-dependent carrier mobilities of monolayer IrSCl and IrSI by using the Boltzmann transport equation.
表 1 双轴应变下IrSCl和IrSI的有效质量, 电子有效质量计算的是次级导带底的位置, 空穴有效质量计算的是价带顶位置
Table 1. Effective masses of IrSCl and IrSI under biaxial strain. The effective mass of electrons is at the CBM' point, and the effective mass of holes is at the VBM point
$\Delta \varepsilon$ $m_{x, {\rm{h}}} (m_{\mathrm{e}} )$ $m_{x, {\rm{e}}} (m_{\mathrm{e}} )$ $m_{y, {\rm{h}}} (m_{\mathrm{e}} )$ $m_{y, {\rm{e}}} (m_{\mathrm{e}} )$ IrSCl 0% 1.839 3.300 0.232 0.179 2% 1.781 3.470 0.223 0.181 4% 1.761 3.690 0.304 0.187 6% 1.785 3.861 0.379 0.196 IrSI 0% 2.295 1.337 0.244 0.238 2% 2.187 1.397 0.260 0.224 4% 2.126 1.452 0.279 0.215 6% 2.134 1.512 0.300 0.205 
下载: 导出CSV
表 2 基于形变势理论计算单层IrSCl和IrSI的弹性模量(J/m2)、形变势(eV)和载流子迁移率(cm2/(V·s))
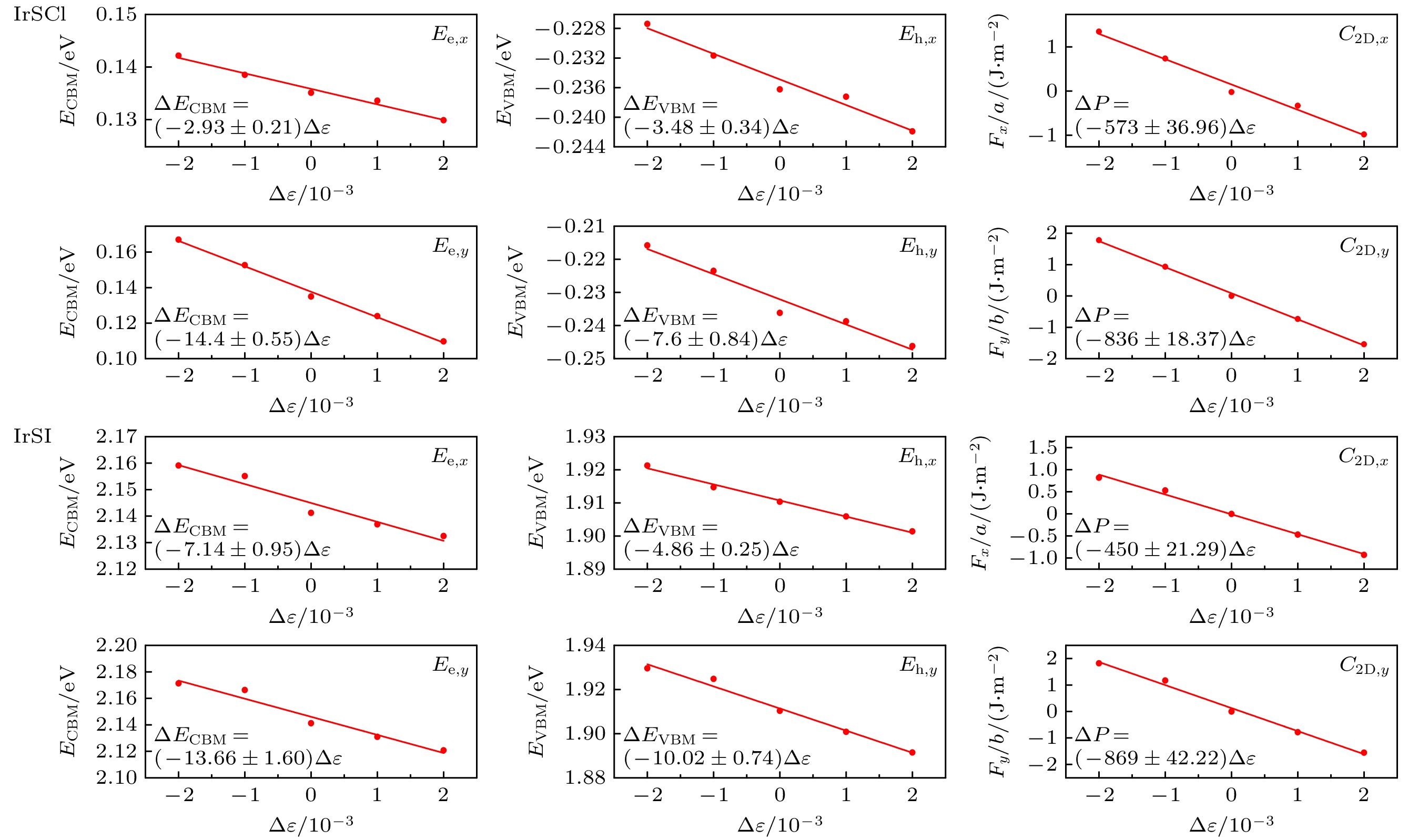
Table 2. Based on the deformation potential theory, the elastic modulus (J/m2), deformation potential (eV), and carrier mobility (cm2/(V·s)) of monolayer IrSCl and IrSI were calculated.
$C_{2\mathrm{D}, x} $ $C_{2\mathrm{D}, y} $ $E_{{\rm{h}}, x} $ $E_{{\rm{e}}, x} $ $E_{{\rm{h}}, y} $ $E_{{\rm{e}}, y} $ $\mu _{{\rm{h}}, x} $ $\mu _{{\rm{e}}, x} $ $\mu _{{\rm{h}}, y} $ $\mu _{{\rm{e}}, y} $ IrSCl 114.6 167.2 3.48 2.93 7.6 14.4 168.5 112.84 407.77 161.88 IrSI 90 173.8 4.86 7.14 10.02 13.66 47.49 50.14 202.64 148.9
下载: 导出CSV
表 3 基于玻尔兹曼输运方程计算得到的不同温度下单层IrSCl和IrSI的载流子迁移率
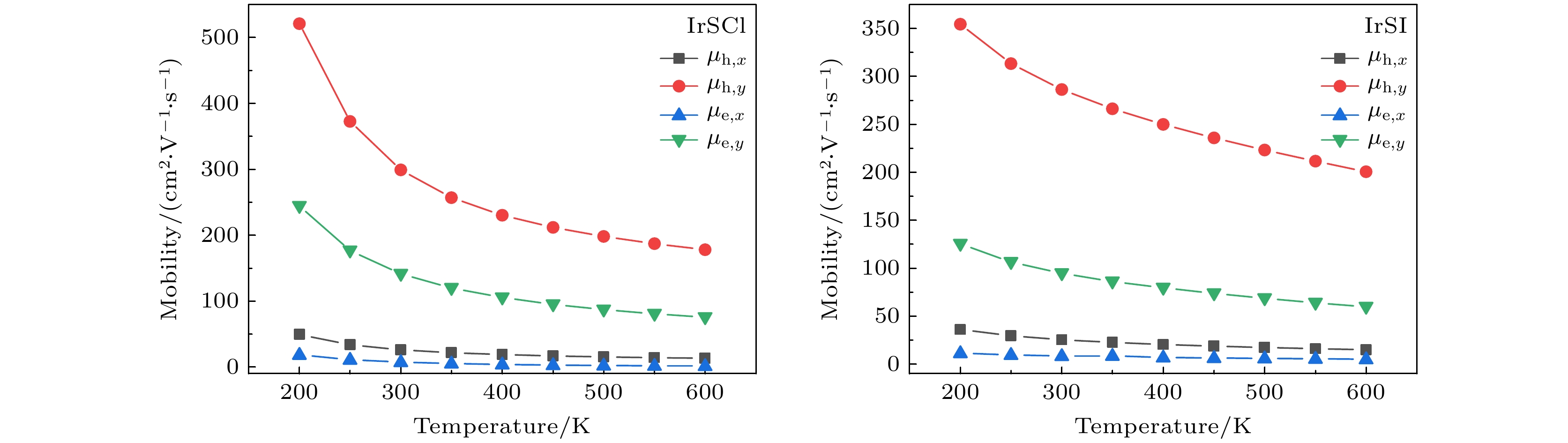
Table 3. Calculated temperature-dependent carrier mobilities of monolayer IrSCl and IrSI by using the Boltzmann transport equation.
Temperature/K IrSCl IrSI $\mu _{{\rm{h}}, x} $ $\mu _{{\rm{h}}, y} $ $\mu _{{\rm{e}}, x} $ $\mu _{{\rm{e}}, y} $ $\mu _{{\rm{h}}, x} $ $\mu _{{\rm{h}}, y} $ $\mu _{{\rm{e}}, x} $ $\mu _{{\rm{e}}, y} $ 200 49.41 520.94 18.70 244.38 36.11 354.48 11.48 125.45 250 33.86 372.70 11.29 176.83 29.55 313.42 9.59 106.41 300 26.20 299.15 7.57 141.39 25.44 286.41 8.44 94.75 350 21.80 257.10 5.44 119.99 22.58 266.34 8.63 86.15 400 18.98 230.42 4.09 105.65 20.44 250.04 6.99 79.58 450 17.00 211.99 3.18 95.26 18.73 235.97 6.45 73.77 500 15.51 198.26 2.54 87.28 17.32 223.31 5.98 68.61 550 14.34 187.32 2.07 80.89 16.11 211.64 5.56 63.96 600 13.36 178.08 1.72 75.61 15.05 200.68 5.18 59.72
下载: 导出CSV
-
[1] Feng L P, Li A, Wang P C, Liu Z T 2018 J. Phys. Chem. C 42 122
Google Scholar
[2] Su Y, Cao S, Shi L B, Qian P 2020 Appl. Surf. Sci. 531 147341
Google Scholar
[3] Qu H Z, Zhang S L, Zhou W H, Guo S Y, Zeng H B 2020 IEEE Electron Device Lett. 41 1029
Google Scholar
[4] Li Q, Du B D, Gao J Y, Liu J 2023 Appl. Phys. Rev. 10 011402
Google Scholar
[5] Guo S Y, Wang Y, Qu H Z, Zhou W H, Ang Y S, Zhang S L, Zeng H B 2024 Phys. Rev. Appl. 21 054016
Google Scholar
[6] Shi H, Yang S Y, Wang H P, Ding D P, Hu Y, Qu H Z, Chen C Y, Hu X M, Zhang S L 2024 ACS Appl. Mater. Interfaces 16 39592
Google Scholar
[7] Song Y, Pan J B, Zhang Y F, Yang H T, Du S X 2021 J. Phys. Chem. Lett. 12 6007
Google Scholar
[8] Whitfield G, Shaw P B 1980 Phys. Rev. B 21 4349
Google Scholar
[9] Zunger A 2019 Nature 566 447
Google Scholar
[10] Göser O, Paul W, Kahle H G 1990 J. Magn. Magn. Mater. 92 129
Google Scholar
[11] Fei R X, Yang L 2014 Nano Lett. 14 2884
Google Scholar
[12] Qiao J S, Kong X H, Hu Z X, Yang F, Ji W 2014 Nat. Commun. 5 4475
Google Scholar
[13] Lang H F, Zhang S Q, Liu Z R 2016 Phys. Rev. B 94 235306
Google Scholar
[14] Generazio E R, Spector H N 1979 Phys. Rev. B 20 5162
Google Scholar
[15] Shi L B, Zhang Y Y, Xiu X M, Dong H K 2018 Carbon 134 103
Google Scholar
[16] Zhang Y J, Cao S, Wang Y Z, Jian X D, Shi L B, Qian P 2021 Phys. Lett. A 401 127340
Google Scholar
[17] Poncé S, Jena D, Giustino F 2019 Phys. Rev. B 100 085204
Google Scholar
[18] Poncé S, Jena D, Giustino F 2019 Phys. Rev. Lett. 123 096602
Google Scholar
[19] Poncé S, Li W, Reichardt S, Giustino F 2020 Rep. Prog. Phys. 83 036501
Google Scholar
[20] Alidoosty-Shahraki M, Bashirpour M 2020 IEEE Trans. Electron Devices 67 3459
Google Scholar
[21] Shi L B, Cao S, Yang M, You Q, Zhang K C, Bao Y, Zhang Y J, Niu Y Y, Qian P 2019 J. Phys.: Condens. Matter 32 065306
Google Scholar
[22] Su Y, Li N, Shi L B, Wang L Z, Qian P 2022 Comput. Mater. Sci. 213 111609
Google Scholar
[23] 王晓艳, 张鹤鸣, 宋建军, 马建立, 王冠宇, 安久华 2011 60 077205
Google Scholar
Wang X Y, Zhang H M, Song J J, Ma J L, Wang G Y, An J H 2011 Acta Phys. Sin. 60 077205
Google Scholar
[24] Hamann D, Schlüter M, Chiang C 1979 Phys. Rev. Lett. 43 1494
Google Scholar
[25] Perdew J, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[26] Baroni S, Giannozzi P 2009 AGU Fall Meet. Abstr. 21 395502
Google Scholar
[27] Itvinov I V 2006 Appl. Phys. Lett. 89 43
Google Scholar
[28] Noffsinger J, Giustino F, Malone B D, Park C H, Louie S G, Cohen M L 2010 Comput. Phys. Commun. 181 2140
Google Scholar
下载:
计量
- 文章访问数: 576
- PDF下载量: 27
- 被引次数: 0
