-
准二维的杂化非本征铁电体在实现强磁电耦合的单相室温多铁性方面具有很大的潜力, 然而此类陶瓷样品通常有着较高的矫顽场和较低的剩余极化强度, 严重阻碍了对其的研究和应用. 本文成功制备了质量高且单相性较好的具有准二维结构的双层R-P(Ruddlesden-Popper)型氧化物Sr3Sn2–xGexO7陶瓷样品, 观察到了较高的剩余极化和与Sr3Sn2O7单晶接近的矫顽场. 微量Ge元素对B位Sn掺杂后极化强度显著增强, 同时进一步降低了Sr3Sn2O7样品的矫顽场. 结合晶格动力学研究, 对样品的拉曼和红外光谱进行标定, 得出掺杂样品铁电性能的增强可能源于氧八面体倾侧幅度的增大和旋转幅度减小. Berry相位法和玻恩有效电荷模型进一步证实了铁电性能的增强. 通过紫外可见光光度计测试得到Sr3Sn2O7样品的光学带隙为3.91 eV, 采用Becke-Johnson势结合局部密度近似(MBJ-LDA)所计算的结果与实验基本一致. 总之, 这项研究为此类杂化非本征铁电体的制备及铁电性能的调控提供了参考, 有望促进铁电陶瓷在各种电容器和非易失性存储器件中的广泛应用.Hybrid improper ferroelectricity with quasi-two-dimensional (quasi-2D) structure has attracted much attention recently due to its great potential in realizing strong magnetoelectric coupling and room-temperature multiferroicity in a single phase. However, recent studies show that there appears high coercive field and low remnant polarization in ceramics, which severely hinders the applications of this material. In this work, high-quality Sr3Sn2O7 and Sr3Sn1.99Ge0.01O7 ceramics with a Ruddlesden-Popper (R-P) structure are successfully prepared, and their crystal structures and electrical properties are investigated in detail. It is found that the Sr3Sn2O7 ceramic exhibits a lower coercive field that is close to that of Sr3Sn2O7 single crystal. Moreover, via a small amount of Ge doping, the polarization reaches 0.34 μC/cm2 for Sr3Sn2O7 and 0.61 μC/cm2 for Sr3Sn1.99Ge0.01O7. Combining crystal lattice dynamic studies, we analyze the Raman and infrared responses of the samples, showing the information about the tilting and rotation of the oxygen octahedra in the samples. The improved ferroelectricity after doping may be attributed to the increased amplitude of the tilt mode and the reduced amplitude of rotation mode. Besides, the enhanced ferroelectric properties through Ge doping and its mechanism are further investigated by the Berry phase approach and the Born effective charge method. Furthermore, via the UV-visible spectra, the optical bandgap is determined to be 3.91 eV for Sr3Sn2O7 ceramic and 3.95 eV for Sr3Sn1.99Ge0.01O7 ceramic. Using the Becke-Johnson potential combined with the local density approximation correlation, the bandgap is calculated and is found to be in close agreement with the experimental result. And the electronic excitations can be assigned to the charge transfer excitation from O 2p to Sn 5s (Ge 4s). The effects of Ge doping on the ability of Sr3Sn2O7 to gain and lose electrons and the bonding strength of Sn-O bond are analyzed via two-dimensional charge density difference. In conclusion, this study provides insights into the synthesis method and modulation of ferroelectric properties of hybrid improper ferroelectrics Sr3Sn2O7, potentially facilitating their widespread applications in various capacitors and non-volatile memory devices.
-
Keywords:
- Sr3Sn2O7 /
- hybrid improper ferroelectricity /
- oxygen octahedron tilt and rotation /
- first-principles study
[1] Scott J F 2007 Science 315 954
Google Scholar
[2] Haertling G H 1999 J. Am. Ceram. Soc. 82 797
Google Scholar
[3] Benedek N A, Fennie C J 2011 Phys. Rev. Lett. 106 107204
Google Scholar
[4] 刘小强, 吴淑雅, 朱晓莉, 陈湘明 2018 67 50
Google Scholar
Liu X Q, Wu S Y, Zhu X L, Chen X M 2018 Acta Phys. Sin. 67 50
Google Scholar
[5] Zhang H W, Yuan K J, Tang H, Zheng P F, Zhou W, Wang C, Liu W F 2023 J. Solid State Chem. 325 124180
Google Scholar
[6] Wu X X, Wang S Y, Wong-Ng W, Gu Q, Jiang Y, Wang C, Ma S, Liu W F 2021 J. Adv. Ceram. 10 120
Google Scholar
[7] Wang Y Z, Huang F T, Luo X, Gao B, Cheong S W 2017 Adv. Mater. 29 1601288
Google Scholar
[8] Xu X H, Wang Y Z, Huang F T, Du K, Nowadnick E A, Cheong S W 2020 Adv. Funct. Mater. 30 2003623
Google Scholar
[9] Gu Q, Liu W F, Wong-Ng W, Wu X X, Wang C, Zhou W, Wang S Y 2021 J. Electroceram. 47 42
Google Scholar
[10] Lu J J, Liu X Q, Ma X, Fu M S, Yuan A, Wu Y J, Chen X M 2019 J. Appl. Phys. 125 044101
Google Scholar
[11] Chen B H, Sun T L, Liu X Q, Zhu X L, Tian H, Chen X M 2020 Appl. Phys. Lett. 116 042903
Google Scholar
[12] Chen Q S, Zhang B H, Chen B H, Liu X Q, Chen X M 2022 J. Appl. Phys. 131 184102
Google Scholar
[13] Wu H D, Gao Z Y, Cai W, Gao R, Chen D, Chen G, Deng X, Wang Z, Lei X, Wang X Y, Fu C 2022 Mater. Today Chem. 26 101226
Google Scholar
[14] Fukasawa I, Maruyama Y, Yoshida S, Fujita K, Takahashi H, Ohgaki M, Nagao M, Watauchi S, Gopalan V, Tanaka K, Tanaka I 2023 J. Cryst. Growth 615 127241
Google Scholar
[15] Xiao Z F, Xiao T Q, Wang S Y, Huang S, Wei B D, Liu W F 2024 J. Am. Ceram. Soc. 107 334
Google Scholar
[16] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[17] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
Google Scholar
[18] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2008 Phys. Rev. Lett. 100 136406
Google Scholar
[19] Becke A D, Johnson E R 2006 J. Chem. Phys. 124 221101
Google Scholar
[20] Baroni S, de Gironcoli S, Dal Corso A, Giannozzi P 2001 Rev. Mod. Phys. 73 515
Google Scholar
[21] Togo A, Tanaka I 2015 Scr. Mater. 108 1
Google Scholar
[22] Resta R 1994 Rev. Mod. Phys. 66 899
Google Scholar
[23] Meyer B, Vanderbilt D 2002 Phys. Rev. B 65 104111
Google Scholar
[24] Kroumova E, Aroyo M I, Perez-Mato J M, Kirov A, Capillas C, Ivantchev S, Wondratschek H 2003 Phase Transitions 76 155
Google Scholar
[25] Skelton J M, Burton L A, Jackson A J, Oba F, Parker S C, Walsh A 2017 Phys. Chem. Chem. Phys. 19 12452
Google Scholar
[26] Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272
Google Scholar
[27] Wiles D B, Young R A 1981 J. Appl. Crystallogr. 14 149
Google Scholar
[28] Lufaso M W, Woodward P M 2004 Acta Crystallogr. , Sect. B 60 10
Google Scholar
[29] Liu X Q, Chen B H, Lu J J, Hu Z Z, Chen X M 2018 Appl. Phys. Lett. 113 242904
Google Scholar
[30] Fawcett I D, Kim E, Greenblatt M, Croft M, Bendersky L A 2000 Phys. Rev. B 62 6485
Google Scholar
[31] Huang L F, Lu X Z, Rondinelli J M 2016 Phys. Rev. Lett. 117 115901
Google Scholar
[32] Mulder A T, Benedek N A, Rondinelli J M, Fennie C J 2013 Adv. Funct. Mater. 23 4810
Google Scholar
[33] 黄昆 2012 固体物理学 (北京: 高等教育出版社) 第78页
Huang K 2012 Solid State Physics (Beijing: Higher Education Press) p78
[34] Smith K A, Ramkumar S P, Harms N C, Clune A J, Xu X, Cheong S W, Liu Z, Nowadnick E A, Musfeldt J L 2021 Phys. Rev. B 104 064106
Google Scholar
[35] Yuan K J, Zhang H W, Gu Q, Xiao T Q, Li Z Y, Wong-Ng W K, Zhou W, Wang C, Wang S Y, Liu W F 2023 J. Am. Ceram. Soc. 106 2455
Google Scholar
[36] Sun X F, Yang X M, Xu C, Gan X C, Zhang W J, Gao Z R, Cai H L, Wu X S 2019 Chem. Phys. Lett. 728 74
Google Scholar
[37] Singh M K, Karan N K, Katiyar R S, Scott J F, Jang H M 2008 J. Phys. : Condens. Matter 20 055210
Google Scholar
[38] Spaldin N A 2012 J. Solid State Chem. 195 2
Google Scholar
[39] Neaton J B, Ederer C, Waghmare U V, Spaldin N A, Rabe K M 2005 Phys. Rev. B 71 014113
Google Scholar
[40] Filip L D, Plugaru N, Pintilie L 2019 Modell. Simul. Mater. Sci. Eng. 27 045008
Google Scholar
[41] Kamimura S, Obukuro Y, Matsushima S, Nakamura H, Arai M, Xu C N 2015 J. Solid State Chem. 232 163
Google Scholar
[42] Tauc J, Grigorovici R, Vancu A 1966 Phys. Status. 15 627
Google Scholar
[43] Kamimura S, Yamada H, Xu C N 2012 Appl. Phys. Lett. 101 091113
Google Scholar
[44] Kumaradhas P, Gopalan R S, Kulkarni G U 1999 Proc. Indian Acad. Sci. (Chem. Sci.) 111 569
Google Scholar
-
图 1 (a) Sr3Sn2–xGexO7 (x = 0, 0.01)的室温XRD图谱; (b) Sr3Sn2O7的晶体结构示意图; (c), (d)分别为氧八面体的倾侧角和旋转角
Fig. 1. (a) The XRD patterns of Sr3Sn2–xGexO7(x = 0, 0.01); (b) crystal structure of Sr3Sn2O7; (c), (d) are the oxygen octahedral tilt angle and rotation angle respectively.
图 2 Sr3Sn2O7的声子色散谱, 及原子和方向分辨的声子态密度(gν)谱
Fig. 2. Phonon dispersions, atom and direction-resolved phonon density of states (gν).
图 3 Sr3Sn2O7和Sr3Sn1.99Ge0.01O7陶瓷在室温下的 (a)红外响应(彩色符号表示预测的模式位置、对称性和强度); (b)红外吸收光谱峰拟合和(c)Raman光谱
Fig. 3. (a) Infrared response (Colored symbols indicate predicted mode positions, symmetries, and intensities); (b) peak-fitting infrared absorption spectra; (c) Raman spectra of Sr3Sn2O7 and Sr3Sn1.99Ge0.01O7.
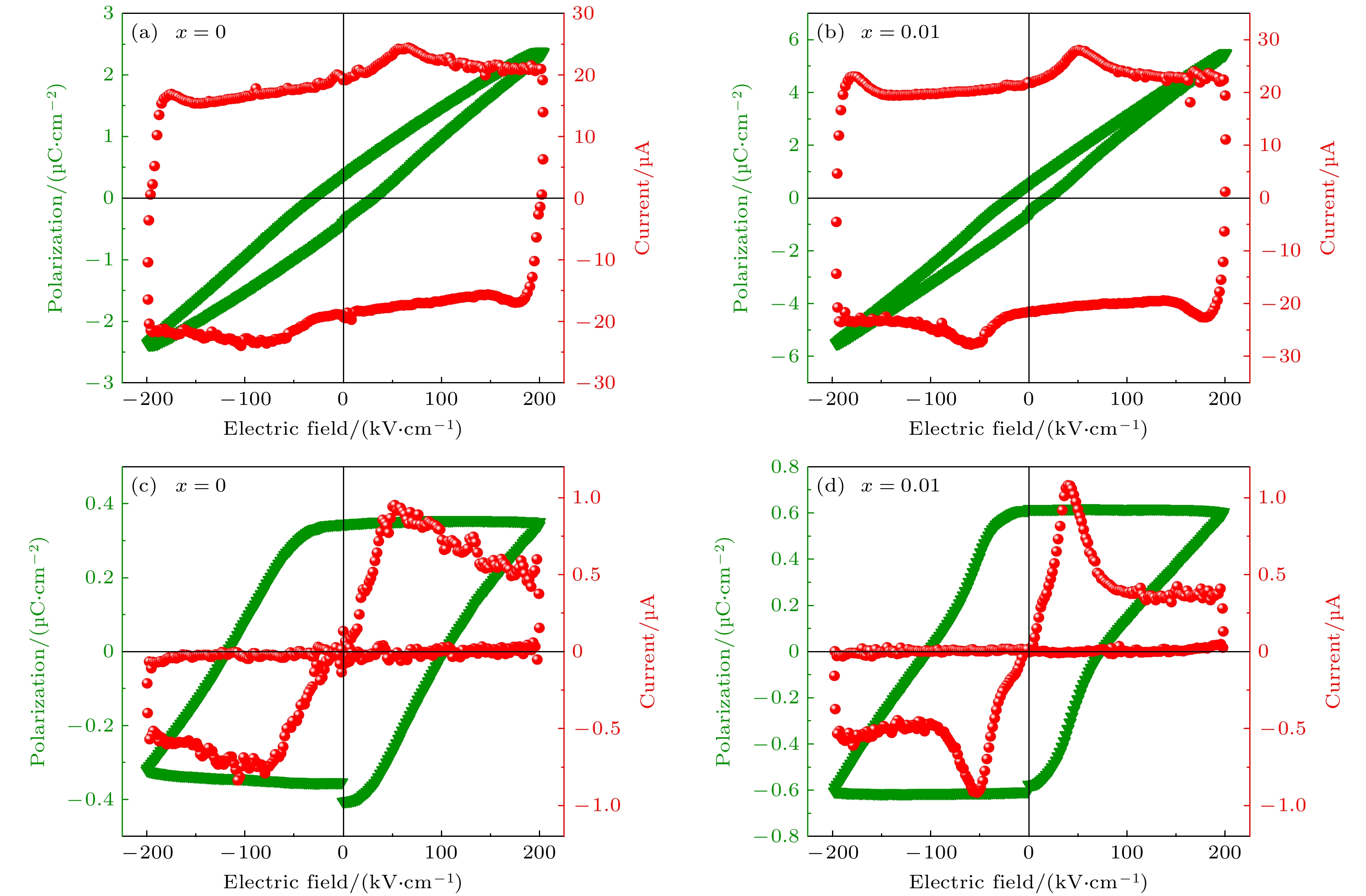
图 4 在DHM模式下频率为100 Hz时(a) Sr3Sn2O7和(b) Sr3Sn1.99Ge0.01O7陶瓷的P-E和I-E曲线; (c), (d) Sr3Sn2O7和Sr3Sn1.99Ge0.01O7陶瓷在10 Hz频率下通过PUND获得的P-E和I-E曲线
Fig. 4. At frequency of 100 Hz in DHM mode: P-E loops and displacement current recorded of (a) Sr3Sn2O7, (b) Sr3Sn1.99Ge0.01O7; P-E loops of Sr3Sn2O7 and Sr3Sn1.99Ge0.01O7 ceramics obtained at frequency of 10 Hz by PUND measurement for (c) and (d), respectively.
图 5 (a) Sr3Sn2O7和(b) Ge-Sr3Sn2O7的极化值(P)沿A21am铁电结构(λ = 1)到I4/mmm中心对称顺电结构(λ = 0)路径的变化
Fig. 5. The change in polarization P of Sr3Sn2O7 and Ge-Sr3Sn2O7 along a path from the ferroelectric structure A21am (λ = 1) to the centrosymmetric paraelectric structure I4/mmm (λ = 0).
图 9 (a) Ge-Sr3Sn2O7的结构示意图; Sr3Sn2O7 (b)和Ge-Sr3Sn2O7 (c)在[001]方向12.3 Å处平面上的二维差分电荷密度图, 等高线间隔为0.005
Fig. 9. (a) The schematic of Ge-Sr3Sn2O7; the two-dimensional charge density difference of Sr3Sn2O7 (b) and Ge doped Sr3Sn2O7 (c) for [001] plane at 12.3 Å.
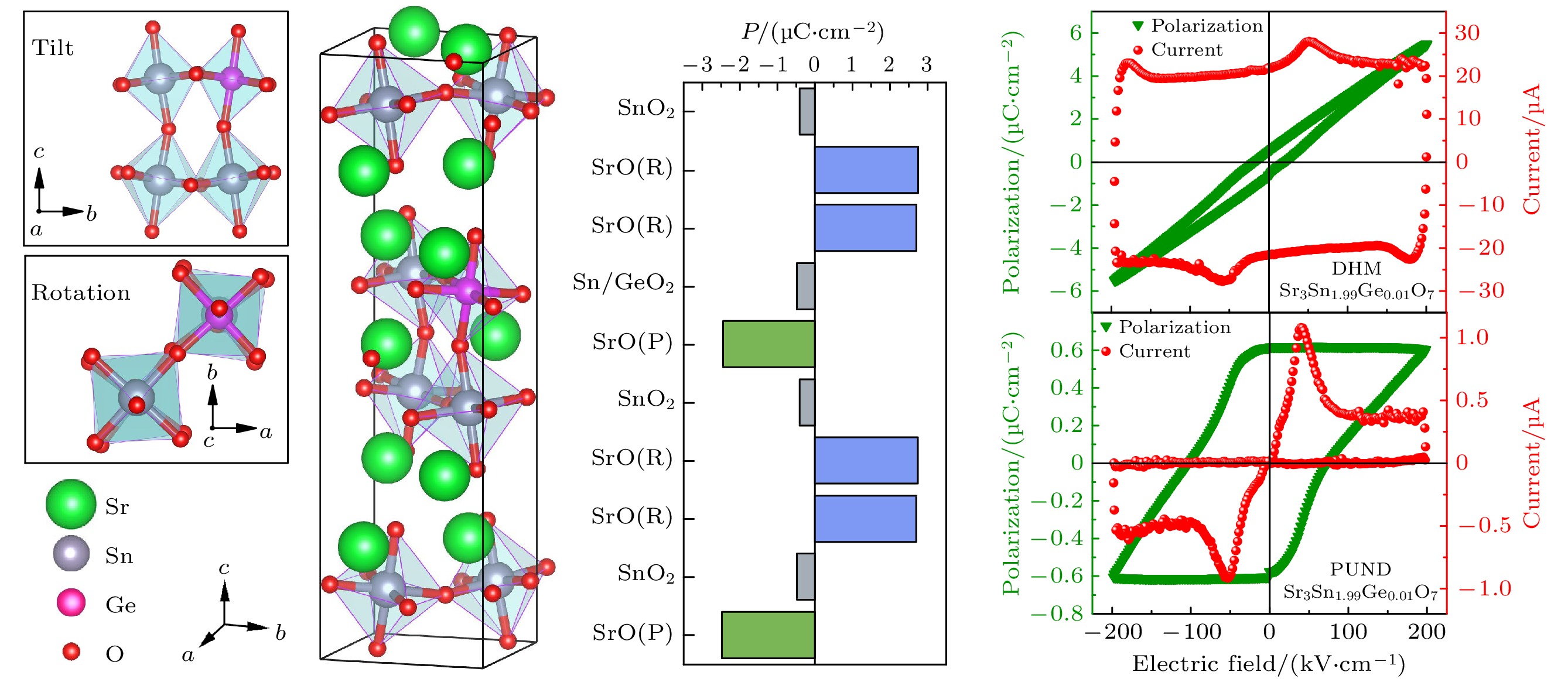
图 6 Sr3Sn2O7沿着a方向(a)原子和(c)逐层对宏观极化贡献; Ge-Sr3Sn2O7沿着a方向(b)原子和(d)逐层对宏观极化贡献(原子标签对应于图1(b), R表示岩盐层处, P表示钙钛矿层处)
Fig. 6. (a), (b) Atomic and (c), (d) layer resolved contributions to macroscopic polarization along a of Sr3Sn2O7 and Ge-Sr3Sn2O7, respectively (atoms correspond to Fig. 1(b), R represents the layer in rock-salt sheets and P represents the layer in perovskite sheets).
图 7 Sr3Sn2O7和Sr3Sn1.99Ge0.01O7陶瓷的(a)漏电流曲线和(b)光吸收谱, 插图为(αhv)2与hv的关系
Fig. 7. (a) The leakage current density as a function of applied electric field for Sr3Sn2O7 and Sr3Sn1.99Ge0.01O7 ceramics; (b) UV-Vis absorption spectra of Sr3Sn2O7 and Sr3Sn1.99Ge0.01O7 ceramics. Inset: a functional relationship of (αhv)2 and hv.
图 8 Sr3Sn2O7和Ge-Sr3Sn2O7中每个原子轨道的态密度
Fig. 8. Projected density of states (PDOS) of Sr3Sn2O7 and Ge-Sr3Sn2O7, respectively.
表 1 在室温下根据粉末XRD图谱进行Rietveld精修结果得出的室温下Sr3Sn2O7和Sr3Sn1.99Ge0.01O7陶瓷的晶胞参数
Table 1. Structure parameters obtained from rietveld refinement of Sr3Sn2O7 and Sr3Sn1.99Ge0.01O7.
x a/Å b/Å c/Å V/Å3 Sn-O1/Sn-O2 Sn-O3/Sn-O4 Sn-O1-Sn χ2 0 5.7073(5) 5.7275(9) 20.6614(6) 675.39(1) 2.0543/2.0157 2.0519/2.0655 165.5724 9.34 0.01 5.7072(9) 5.7279(8) 20.6537(9) 675.17(5) 2.0746/2.0124 2.0469/2.0253 164.5905 7.63 
下载: 导出CSV
表 A1 Sr3Sn2O7 (空间群: A21am) 在Γ点声子频率的计算值(单位: cm–1)
Table A1. Calculated Γ-point phonon frequencies (in cm–1) of the Sr3Sn2O7 A21am phase.
Mode Freq. Mode Freq. Mode Freq. Mode Freq. A1(1) 83.45 A2(1) 84.32 B1(1) 79.63 B2(1) 98.83 A1(2) 106.1 A2(2) 95.39 B1(2) 120.98 B2(2) 105.36 A1(3) 113.74 A2(3) 117.77 B1(3) 135.12 B2(3) 120.32 A1(4) 137.11 A2(4) 143.61 B1(4) 145.26 B2(4) 146.46 A1(5) 161.92 A2(5) 151.16 B1(5) 152.96 B2(5) 147.76 A1(6) 169.23 A2(6) 167.5 B1(6) 177.96 B2(6) 171.62 A1(7) 180.04 A2(7) 184.97 B1(7) 222.77 B2(7) 214.88 A1(8) 205.98 A2(8) 224.54 B1(8) 235.61 B2(8) 228.54 A1(9) 218.41 A2(9) 270.38 B1(9) 256.1 B2(9) 239.46 A1(10) 235.43 A2(10) 282.2 B1(10) 284.18 B2(10) 268.64 A1(11) 259.61 A2(11) 312.19 B1(11) 335.67 B2(11) 309.89 A1(12) 268.83 A2(12) 323.99 B1(12) 357.18 B2(12) 320.91 A1(13) 335.88 A2(13) 389.97 B1(13) 501.68 B2(13) 335.2 A1(14) 380.89 A2(14) 481.55 B1(14) 552.45 B2(14) 351.21 A1(15) 421.45 A2(15) 566.25 B1(15) 610.85 B2(15) 404.25 A1(16) 504.49 A2(16) 620.55 B1(16) 657.19 B2(16) 510.89 A1(17) 572.78 A2(17) 717.72 B2(17) 623.74 A1(18) 610.09 B2(18) 708.57
下载: 导出CSV
表 A2 计算的沿着a方向各个原子的玻恩有效电荷和从高对称的顺电相I4/mmm到低对称的铁电相A21am的相对原子位移
Table A2. The calculated Born effective charges and relative atomic displacements along a direction from the high symmetry I4/mmm to distorted A21am positions.
Atom $Z^*$ Atom $Z^*$ ∆x Sr1 2.50(6) Sr1 2.51(3) –0.04(8) Sr2 2.33(1) Sr2 2.34(6) 0.37(2) Sn 4.22(0) Sn/Ge 4.25(2)/4.37(7) 0.15(0) O1 –1.75(2) O1 –1.73(6) 0.14(0 O2 –1.93(2) O2 –1.93(2) 0.03(5) O3 –2.49(8) O3 –2.53(4) 0.42(2) O4 –2.49(8) O4 –2.53(7) –0.11(7)
下载: 导出CSV
-
[1] Scott J F 2007 Science 315 954
Google Scholar
[2] Haertling G H 1999 J. Am. Ceram. Soc. 82 797
Google Scholar
[3] Benedek N A, Fennie C J 2011 Phys. Rev. Lett. 106 107204
Google Scholar
[4] 刘小强, 吴淑雅, 朱晓莉, 陈湘明 2018 67 50
Google Scholar
Liu X Q, Wu S Y, Zhu X L, Chen X M 2018 Acta Phys. Sin. 67 50
Google Scholar
[5] Zhang H W, Yuan K J, Tang H, Zheng P F, Zhou W, Wang C, Liu W F 2023 J. Solid State Chem. 325 124180
Google Scholar
[6] Wu X X, Wang S Y, Wong-Ng W, Gu Q, Jiang Y, Wang C, Ma S, Liu W F 2021 J. Adv. Ceram. 10 120
Google Scholar
[7] Wang Y Z, Huang F T, Luo X, Gao B, Cheong S W 2017 Adv. Mater. 29 1601288
Google Scholar
[8] Xu X H, Wang Y Z, Huang F T, Du K, Nowadnick E A, Cheong S W 2020 Adv. Funct. Mater. 30 2003623
Google Scholar
[9] Gu Q, Liu W F, Wong-Ng W, Wu X X, Wang C, Zhou W, Wang S Y 2021 J. Electroceram. 47 42
Google Scholar
[10] Lu J J, Liu X Q, Ma X, Fu M S, Yuan A, Wu Y J, Chen X M 2019 J. Appl. Phys. 125 044101
Google Scholar
[11] Chen B H, Sun T L, Liu X Q, Zhu X L, Tian H, Chen X M 2020 Appl. Phys. Lett. 116 042903
Google Scholar
[12] Chen Q S, Zhang B H, Chen B H, Liu X Q, Chen X M 2022 J. Appl. Phys. 131 184102
Google Scholar
[13] Wu H D, Gao Z Y, Cai W, Gao R, Chen D, Chen G, Deng X, Wang Z, Lei X, Wang X Y, Fu C 2022 Mater. Today Chem. 26 101226
Google Scholar
[14] Fukasawa I, Maruyama Y, Yoshida S, Fujita K, Takahashi H, Ohgaki M, Nagao M, Watauchi S, Gopalan V, Tanaka K, Tanaka I 2023 J. Cryst. Growth 615 127241
Google Scholar
[15] Xiao Z F, Xiao T Q, Wang S Y, Huang S, Wei B D, Liu W F 2024 J. Am. Ceram. Soc. 107 334
Google Scholar
[16] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[17] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
Google Scholar
[18] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2008 Phys. Rev. Lett. 100 136406
Google Scholar
[19] Becke A D, Johnson E R 2006 J. Chem. Phys. 124 221101
Google Scholar
[20] Baroni S, de Gironcoli S, Dal Corso A, Giannozzi P 2001 Rev. Mod. Phys. 73 515
Google Scholar
[21] Togo A, Tanaka I 2015 Scr. Mater. 108 1
Google Scholar
[22] Resta R 1994 Rev. Mod. Phys. 66 899
Google Scholar
[23] Meyer B, Vanderbilt D 2002 Phys. Rev. B 65 104111
Google Scholar
[24] Kroumova E, Aroyo M I, Perez-Mato J M, Kirov A, Capillas C, Ivantchev S, Wondratschek H 2003 Phase Transitions 76 155
Google Scholar
[25] Skelton J M, Burton L A, Jackson A J, Oba F, Parker S C, Walsh A 2017 Phys. Chem. Chem. Phys. 19 12452
Google Scholar
[26] Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272
Google Scholar
[27] Wiles D B, Young R A 1981 J. Appl. Crystallogr. 14 149
Google Scholar
[28] Lufaso M W, Woodward P M 2004 Acta Crystallogr. , Sect. B 60 10
Google Scholar
[29] Liu X Q, Chen B H, Lu J J, Hu Z Z, Chen X M 2018 Appl. Phys. Lett. 113 242904
Google Scholar
[30] Fawcett I D, Kim E, Greenblatt M, Croft M, Bendersky L A 2000 Phys. Rev. B 62 6485
Google Scholar
[31] Huang L F, Lu X Z, Rondinelli J M 2016 Phys. Rev. Lett. 117 115901
Google Scholar
[32] Mulder A T, Benedek N A, Rondinelli J M, Fennie C J 2013 Adv. Funct. Mater. 23 4810
Google Scholar
[33] 黄昆 2012 固体物理学 (北京: 高等教育出版社) 第78页
Huang K 2012 Solid State Physics (Beijing: Higher Education Press) p78
[34] Smith K A, Ramkumar S P, Harms N C, Clune A J, Xu X, Cheong S W, Liu Z, Nowadnick E A, Musfeldt J L 2021 Phys. Rev. B 104 064106
Google Scholar
[35] Yuan K J, Zhang H W, Gu Q, Xiao T Q, Li Z Y, Wong-Ng W K, Zhou W, Wang C, Wang S Y, Liu W F 2023 J. Am. Ceram. Soc. 106 2455
Google Scholar
[36] Sun X F, Yang X M, Xu C, Gan X C, Zhang W J, Gao Z R, Cai H L, Wu X S 2019 Chem. Phys. Lett. 728 74
Google Scholar
[37] Singh M K, Karan N K, Katiyar R S, Scott J F, Jang H M 2008 J. Phys. : Condens. Matter 20 055210
Google Scholar
[38] Spaldin N A 2012 J. Solid State Chem. 195 2
Google Scholar
[39] Neaton J B, Ederer C, Waghmare U V, Spaldin N A, Rabe K M 2005 Phys. Rev. B 71 014113
Google Scholar
[40] Filip L D, Plugaru N, Pintilie L 2019 Modell. Simul. Mater. Sci. Eng. 27 045008
Google Scholar
[41] Kamimura S, Obukuro Y, Matsushima S, Nakamura H, Arai M, Xu C N 2015 J. Solid State Chem. 232 163
Google Scholar
[42] Tauc J, Grigorovici R, Vancu A 1966 Phys. Status. 15 627
Google Scholar
[43] Kamimura S, Yamada H, Xu C N 2012 Appl. Phys. Lett. 101 091113
Google Scholar
[44] Kumaradhas P, Gopalan R S, Kulkarni G U 1999 Proc. Indian Acad. Sci. (Chem. Sci.) 111 569
Google Scholar
下载:
计量
- 文章访问数: 1537
- PDF下载量: 49
- 被引次数: 0
