-
近年来, 光的轨道角动量自由度的高维度特性引起了广泛的关注. 该自由度在许多科学领域得到了研究和应用, 特别是在光通讯和量子信息领域. 为了充分利用轨道角动量的高维特性, 不同的轨道角动量态的非破坏分离成为一个最基本的要求. 然而, 目前已有的轨道角动量分束系统, 要么在稳定性和级联拓展性方面有所不足; 要么分离后的轨道角动量态的特性遭到严重破坏, 无法参与进一步的相互作用过程. 本文基于光束偏移器构建微型Mach-Zehnder干涉仪, 设计了一个稳定且紧凑的轨道角动量分束器, 实现了轨道角动量模式的非破坏分束. 设计中由于只存在光束的全反射, 因此理论上能量损耗为零. 在微型Mach-Zehnder干涉仪中的光束经过的光学元件相同, 且光束的空间偏移量较小, 所以该轨道角动量分束器具有很好的稳定性. 此外, 由于被分开的轨道角动量态与入射的轨道角动量态具有相同的传播方向, 因此该分束器具有很好的可拓展性, 便于级联使用. 本研究对轨道角动量这一高维自由度在光通讯等相关领域的应用有重要意义.In recent years, the high-dimensional properties of the orbital angular momentum degree of freedom of light have attracted extensive attention. This degree of freedom has been studied and used in many scientific fields, especially in optical communication and quantum information. In order to fully utilize the high-dimensional properties of orbital angular momentum, non-destructive separation of different orbital angular momentum states has become a fundamental requirement. However, the existing orbital angular momentum beam-splitting systems either lack stability and cascade expansibility, or the properties of the separated orbital angular momentum states are seriously damaged, thus failing to participate in further interaction processes. In this work, we construct a miniature Mach-Zehnder interferometer based on the beam displacer, and design an orbital angular momentum beam splitter, thereby realizing the non-destructive beam splitting of orbital angular momentum mode. In the orbital angular momentum splitter, the theoretical energy loss is zero because there exists only total reflection of the beam. The beam in the miniature Mach-Zehnder interferometer passes through the same optical element, and the spatial deviation of the beam is small, so the orbital angular momentum beam splitter has good stability. In addition, because the separated orbital angular momentum state has the same propagation direction as the incident orbital angular momentum state, the beam splitter has good extensibility and is easy to use in cascade. Our research result is of great significance in using the orbital angular momentum as a high-dimensional degree of freedom in optical communication and other related fields.
-
Keywords:
- orbital angular momentum /
- state recognition /
- optical communication
[1] Coullet P, Gil L, Rocca F 1989 Opt. Commun. 73 403
Google Scholar
[2] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[3] Li S M, Kong L J, Ren Z C, Li Y, Tu C, Wang H T 2013 Phys. Rev. A 88 035801
Google Scholar
[4] Neshev D N, Alexander T J, Ostrovskaya E A, Kivshar Y S, Martin H, Makasyuk I, Chen Z 2004 Phys. Rev. Lett. 92 123903
Google Scholar
[5] Swartzlander G A, Law C T 1992 Phys. Rev. Lett. 69 2503
Google Scholar
[6] Tikhonenko V, Christou J, Luther-Daves B 1995 J. Opt. Soc. Am. B 12 2046
Google Scholar
[7] Firth W J, Skryabin D V 1997 Phys. Rev. Lett. 79 2450
Google Scholar
[8] Dholakia K, Simpson N B, Padgett M J, Allen L 1996 Phys. Rev. A 54 R3742
Google Scholar
[9] Courtial J, Dholakia K, Allen L, Padgett M J 1997 Phys. Rev. A 56 4193
Google Scholar
[10] Andersen M F, Ryu C, Cladé P, Natarajan V, Vaziri A, Helmerson K, Phillips W D 2006 Phys. Rev. Lett. 97 170406
Google Scholar
[11] Grier D G 2003 Nature 424 810
Google Scholar
[12] Paterson L, MacDonald M P, Arlt J, Sibbett W, Bryant P E, Dholakia K 2001 Science 292 912
Google Scholar
[13] Kong L J, Qian S X, Ren Z C, Wang X L, Wang H T 2012 Phys. Rev. A 85 035804
Google Scholar
[14] Dennis M R, King R P, Jack B, O’Holleran K, Padgett M J 2010 Nat. Phys. 6 118
Google Scholar
[15] Larocque H, Sugic D, Mortimer D, Taylor A J, Fickler R, Boyd R W, Dennis M R, Karimi E 2018 Nat. Phys. 14 1079
Google Scholar
[16] Wang L, Zhang W X, Yin H X, Zhang X D 2019 Adv. Opt. Mater. 7 1900263
Google Scholar
[17] Kong L J, Zhang W, Li P, Guo X, Zhang J, Zhang F, Zhao J, Zhang X 2022 Nat. Commun. 13 2705
Google Scholar
[18] Fürhapter S, Jesacher A, Bernet S, Ritsch-Marte M 2005 Opt. Express 13 689
Google Scholar
[19] Kozawa Y, Matsunaga D, Sato S 2018 Optica 5 86
Google Scholar
[20] Fang X, Ren H, Gu M 2020 Nat. Photonics 14 102
Google Scholar
[21] Kong L J, Sun Y, Zhang F, Zhang J, Zhang X 2023 Phys. Rev. Lett. 130 053602
Google Scholar
[22] Zhuang X 2004 Science 305 188
Google Scholar
[23] Berkhout G C G, Beijersbergen M W 2008 Phys. Rev. Lett. 101 100801
Google Scholar
[24] Ke Z J, Wang Y T, Yu S, Liu W, Meng Y, Li Z P, Wang H, Li Q, Xu J S, Xiao Y, Tang J S, Li C F, Guo G C 2020 Chin. Phys. B 29 080301
Google Scholar
[25] Friese M E J, Nieminen T A, Heckenberg N R, Rubinsztein-Dunlop H 1998 Nature 394 348
Google Scholar
[26] Friese M E J, Enger J, Rubinsztein-Dunlop H, Heckenberg N R 1996 Phys. Rev. A 54 1593
Google Scholar
[27] Simpson N B, Dholakia K, Allen L, Padgett M J 1997 Opt. Lett. 22 52
Google Scholar
[28] Bialynicki-Birula I, Bialynicka-Birula Z 1997 Phys. Rev. Lett. 78 2539
Google Scholar
[29] Courtial J, Dholakia K, Robertson D A, Allen L, Padgett M J 1998 Phys. Rev. Lett. 80 3217
Google Scholar
[30] Courtial J, Robertson D A, Dholakia K, Allen L, Padgett M J 1998 Phys. Rev. Lett. 81 4828
Google Scholar
[31] Lavery M P J, Speirits F C, Barnett S M, Padgett M J 2013 Science 341 537
Google Scholar
[32] Wang J, Yang J Y, Fazal I M, Ahmed N, Yan Y, Huang H, Ren Y, Yue Y, Dolinar S, Tur M, Willner A E 2012 Nat. Photonics 6 488
Google Scholar
[33] Huang H, Xie G, Yan Y, Ahmed N, Ren Y, Yue Y, Rogawski D, Willner M J, Erkmen B I, Birnbaum K M, Dolinar S J, Lavery M P J, Padgett M J, Tur M, Willner A E 2014 Opt. Lett. 39 197
Google Scholar
[34] Krenn M, Handsteiner J, Fink M, Fickler R, Ursin R, Malik M, Zeilinger A 2016 Proc. Natl. Acad. Sci. 113 13648
Google Scholar
[35] Watkins R J, Dai K, White G, Li W, Miller J K, Morgan K S, Johnson E G 2020 Opt. Express 28 924
Google Scholar
[36] Bozinovic N, Yue Y, Ren Y, Tur M, Kristensen P, Huang H, Willner A E, Ramachandran S 2013 Science 340 1545
Google Scholar
[37] Mair A, Vaziri A, Weihs G, Zeilinger A 2001 Nature 412 313
Google Scholar
[38] Kong L J, Li Y, Liu R, Qi W R, Wang Q, Wang Z X, Huang S Y, Si Y, Tu C, Hu W, Xu F, Lu Y Q, Wang H T 2019 Phys. Rev. A 100 023822
Google Scholar
[39] Kong L J, Liu R, Qi W R, Wang Z X, Huang S Y, Wang Q, Tu C, Li Y, Wang H T 2019 Sci. Adv. 5 eaat9206
Google Scholar
[40] Romero J, Giovannini D, Franke-Arnold S, Barnett S M, Padgett M J 2012 Phys. Rev. A 86 012334
Google Scholar
[41] Vaziri A, Weihs G, Zeilinger A 2002 Phys. Rev. Lett. 89 240401
Google Scholar
[42] Kong L J, Liu R, Qi W R, Wang Z X, Huang S Y, Tu C, Li Y, Wang H T 2020 Chin. Phys. Lett. 37 034204
Google Scholar
[43] Zhang Y, Agnew M, Roger T, Roux F S, Konrad T, Faccio D, Leach J, Forbes A 2017 Nat. Commun. 8 632
Google Scholar
[44] Dada A C, Leach J, Buller G S, Padgett M J, Andersson E 2011 Nat. Phys. 7 677
Google Scholar
[45] Berkhout G C G, Lavery M P J, Courtial J, Beijersbergen M W, Padgett M J 2010 Phys. Rev. Lett. 105 153601
Google Scholar
[46] Wan C, Chen J, Zhan Q 2017 APL Photonics 2 031302
Google Scholar
[47] Wen Y, Chremmos I, Chen Y, Zhu J, Zhang Y, Yu S 2018 Phys. Rev. Lett. 120 193904
Google Scholar
[48] Malik M, Erhard M, Huber M, Krenn M, Fickler R, Zeilinger A 2016 Nat. Photonics 10 248
Google Scholar
[49] Wang F, Erhard M, Babazadeh A, Malik M, Krenn M, Zeilinger A 2017 Optica 4 1462
Google Scholar
[50] Babazadeh A, Erhard M, Wang F, Malik M, Nouroozi R, Krenn M, Zeilinger A 2017 Phys. Rev. Lett. 119 180510
Google Scholar
[51] Wang X L, Luo Y H, Huang H L, Chen M C, Su Z E, Liu C, Chen C, Li W, Fang Y Q, Jiang X, Zhang J, Li L, Liu N L, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 260502
Google Scholar
[52] Cao H, Gao S C, Zhang C, Wang J, He D Y, Liu B H, Zhou Z W, Chen Y J, Li Z H, Yu S Y, Romero J, Huang Y F, Li C F, Guo G C 2020 Optica 7 232
Google Scholar
[53] Leach J, Padgett M J, Barnett S M, Franke-Arnold S, Courtial J 2002 Phys. Rev. Lett. 88 257901
Google Scholar
[54] Wang F X, Chen W, Yin Z Q, Wang S, Guo G C, Han Z F 2016 Phys. Rev. A 94 033847
Google Scholar
[55] Zhang W, Qi Q, Zhou J, Chen L 2014 Phys. Rev. Lett. 112 153601
Google Scholar
[56] Xue P, Zhang R, Bian Z, Zhan X, Qin H, Sanders B C 2015 Phys. Rev. A 92 042316
Google Scholar
[57] Guo P, Wang S 2022 Photonics 10 1
Google Scholar
[58] Narushima T, Okamoto H 2016 Sci. Rep. 6 35731
Google Scholar
[59] Li P, Guo X, Qi S, Han L, Zhang Y, Liu S, Li Y, Zhao J 2018 Sci. Rep. 8 9831
Google Scholar
[60] Chi Y, Yu Y, Gong Q, Wang J 2023 Sci. China Inf. Sci. 66 180501
Google Scholar
[61] Lei T, Zhang M, Li Y R, Jia P, Liu G N, Xu X G, Li Z H, Min C J, Lin J, Yu C Y, Niu H B, Yuan X C 2015 Light Sci. Appl. 4 e257
Google Scholar
-
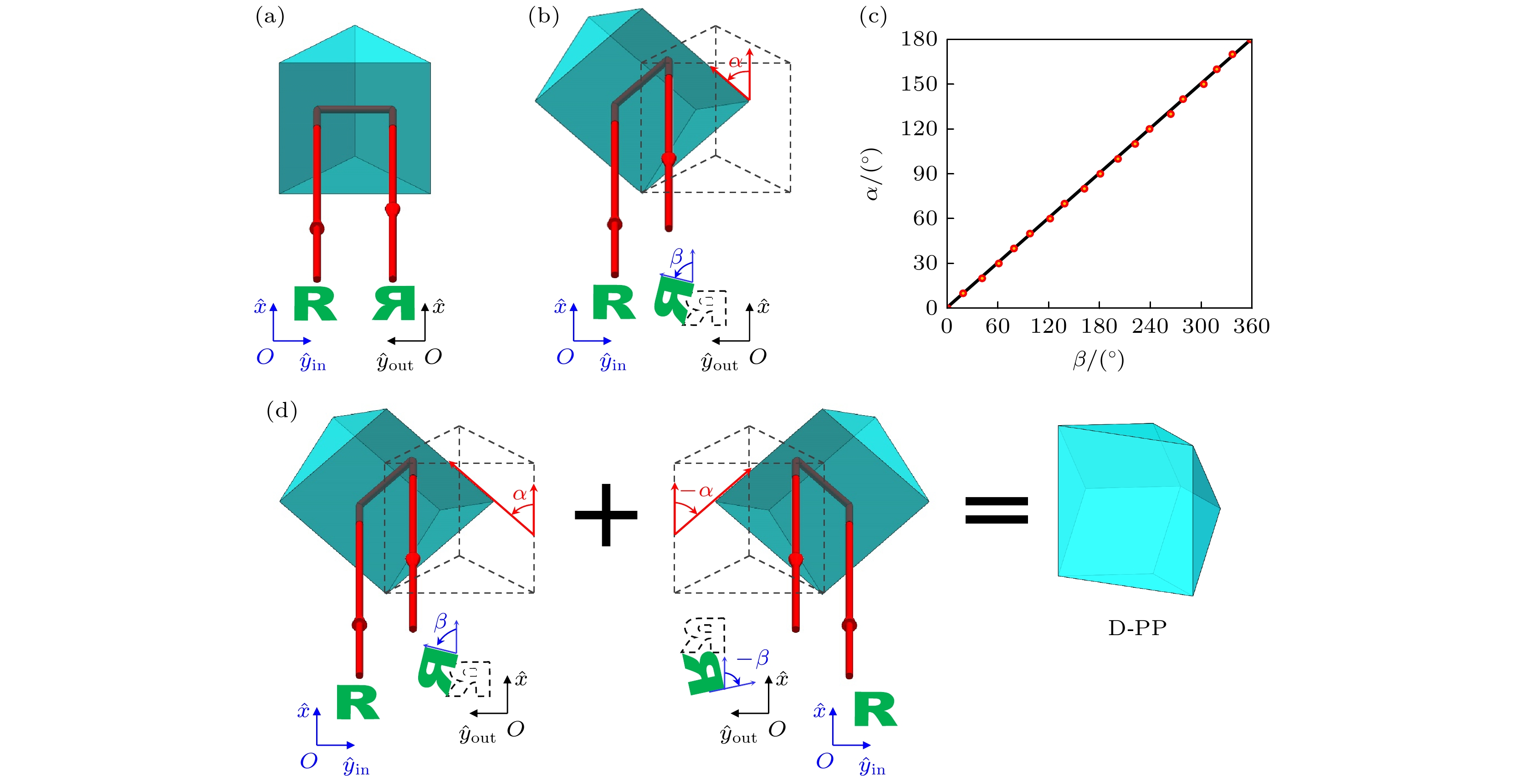
图 1 D-PP对图像的旋转作用 (a)水平放置的PP对图像(绿色字母R)两次反射的情况. 这里, 光束垂直入射到PP的前表面; (b) PP的旋转对图像旋转的影响. 这里, 光束垂直入射到PP的前表面, PP的旋转轴平行于入射光束传播的方向; (c) 以平行于入射光束传播方向为旋转轴, PP相对于水平放置的旋转角度$\alpha $和经过两次反射之后的图像的旋转角度$\beta $之间的关系, 黑色实线为理论结果, 黄色填充的红圈为实验结果; (d) D-PP的构成, 由两个PP构成. 其中一个PP相对于水平放置旋转角度为$\alpha $; 另一个PP相对于水平放置旋转角度为$ - \alpha $
Fig. 1. Rotation effect of D-PP on image: (a) Situation where the image (green letter R) experience two reflections in PP placed horizontally, here, the light field is vertically incident on the front surface of PP; (b) the impact of PP rotation on image rotation, here, the light field is vertically incident on the front surface of PP, and the rotation axis of PP is parallel to the direction of propagation of the incident light field; (c) the relationship between the rotation angle α of the PP and the rotation angle $\beta $of the image after two reflections, the rotation axis is parallel to the propagation direction of the incident light field, the solid black line represents the theoretical results, and the red circles filled in yellow represent the experimental results; (d) composition of D-PP, a D-PP can be seen as a combination of two PPs, the rotation angle of one PP is α, and the rotation angle of another PP is $ - \alpha $.
图 2 基于BD设计的OAM分束器以及不同参数设置下的分束情况 (a) OAM分束器的构成和光路图, 其中, WP1, WP2, WP3表示偏振补偿波片, RP代表直角棱镜, a, a1, a2, b, b1, b2, c, c1, c2, o1, o2表示光束在分束器中所走的路径, 右上角为装置的整体效果图, 左下角为装置的实物图; (b)不同参数情况下的分束情况, $\alpha $为PP旋转的角度, $\delta $为WP1引入的两束正交偏振光之间的相对相位差, $l$为OAM拓扑荷数, ${P_{o1}}$和${P_{o2}}$为输出端口$o1$和$o2$的输出功率
Fig. 2. OAM beam splitter based on BD and beam splitting under different parameter conditions: (a) Composition of the OAM beam splitter and optical path diagram in it. Here, WP1, WP2, and WP3 represent polarization compensation waveplates; RP represents a right-angle prism. a, a1, a2, b, b1, b2, c, c1, c2, o1, o2 indicate the path of the beam in the beam splitter, the upper right corner shows the overall rendering of the device, the lower left corner shows the physical image of the device; (b) beam splitting under different parameter conditions, $\alpha $ is the rotation angle of PP, $\delta $ is the relative phase difference between the two orthogonal polarized beams introduced by WP1, $l$ is the topological charge of OAM, ${P_{o1}}$ and ${P_{o2}}$ are the output powers of the output ports $o1$ and $o2$.
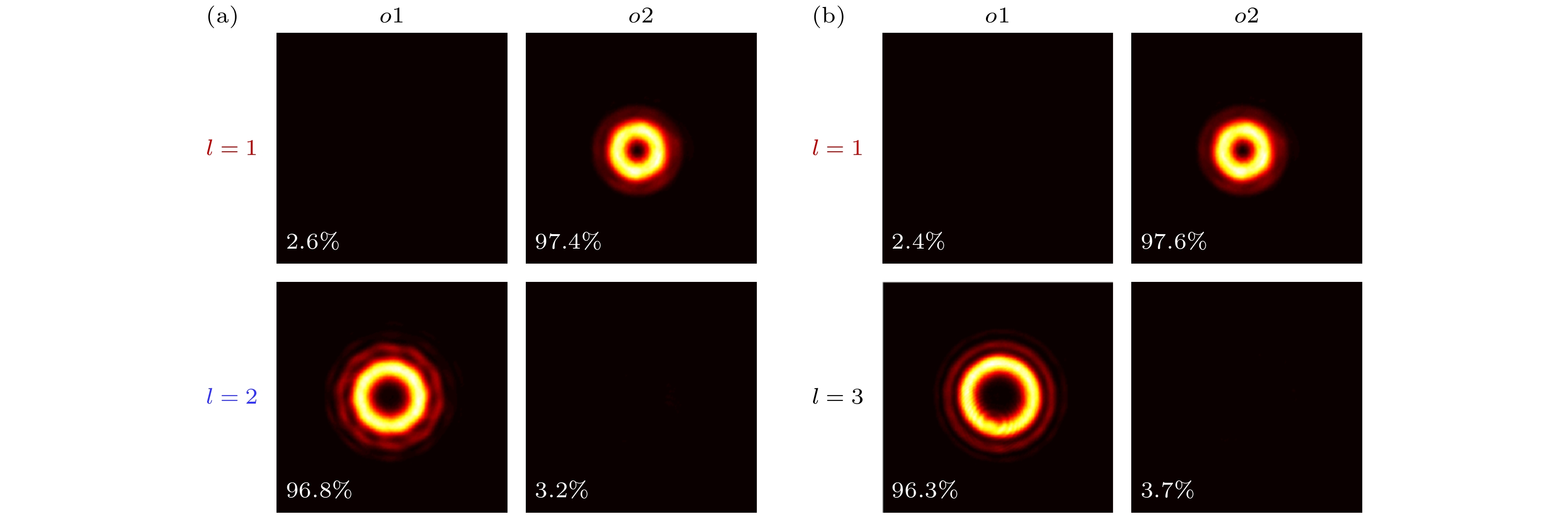
图 3 不同参数下不同拓扑荷数OAM态分束的实验结果 (a)参数设置为$ (\alpha,\; \delta) $ = (π/4, 0)时, OAM态$\left| 1 \right\rangle $和$\left| 2 \right\rangle $分束的结果; (b)参数设置为$ (\alpha,\; \delta) $ = (π/8, π/2)时, OAM态$\left| 1 \right\rangle $和$\left| 3 \right\rangle $分束的结果, 图中的百分数表示对某种入射OAM态, 不同端口的输出功率相对于所有端口输出的总功率的比值
Fig. 3. Experimental results of beam splitting of OAM states with different topological charges in OAM sorter with different parameters: (a) Results of beam splitting of OAM states $\left| 1 \right\rangle $and $\left| 2 \right\rangle $when the parameters are set as $ (\alpha,\; \delta) $ = (π/4, 0); (b) results of beam splitting of OAM states $\left| 1 \right\rangle $and $\left| 3 \right\rangle $when the parameters are set as $ (\alpha,\; \delta) $ = (π/8, π/2), each percentage represents the ratio of each output power to the total output power of all ports for a certain incident OAM state.
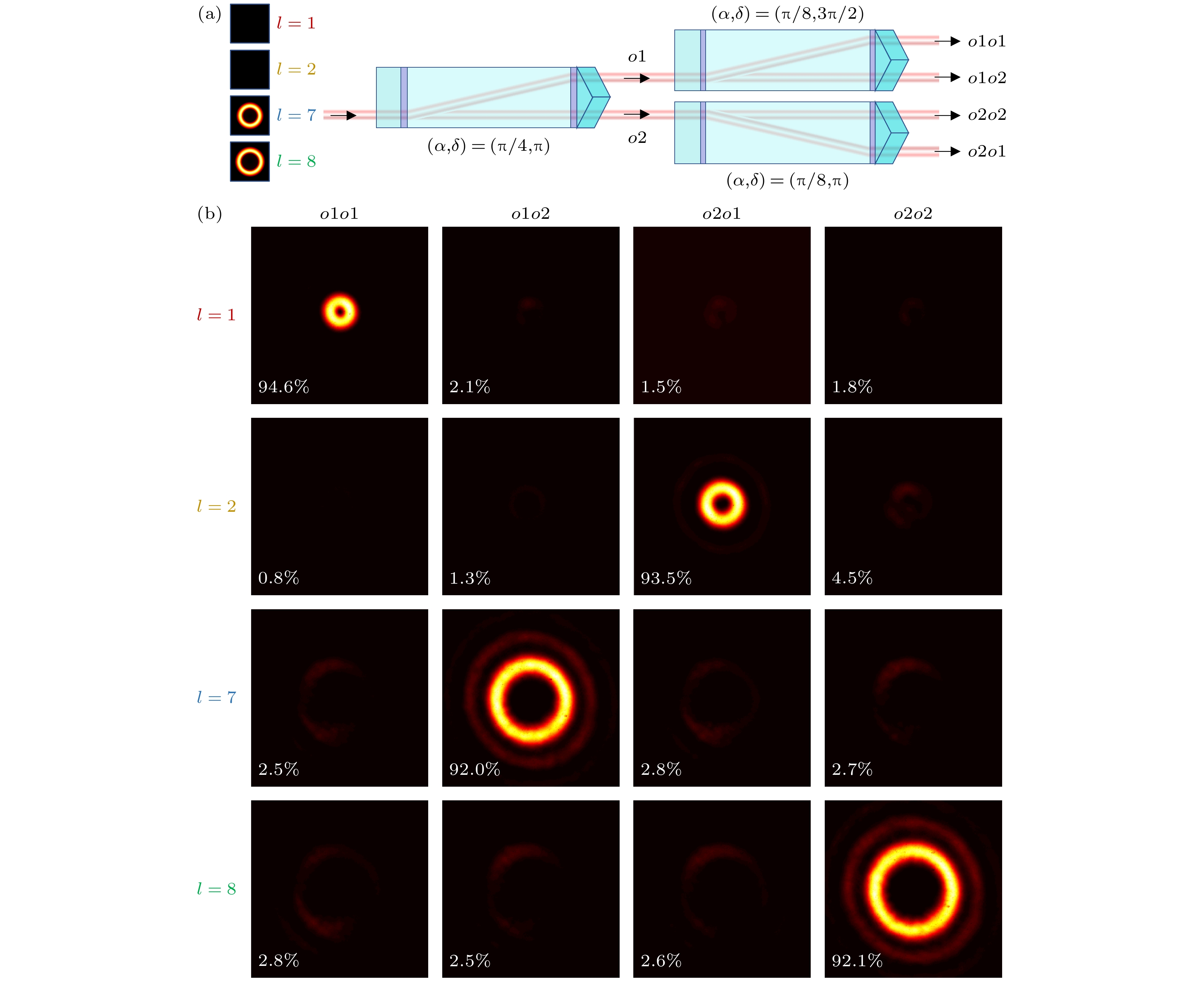
图 4 级联情况下的分束情况 (a)级联OAM分束器. 针对要分开的OAM态为$\left| 1 \right\rangle $, $\left| 2 \right\rangle $, $\left| 7 \right\rangle $和$\left| 8 \right\rangle $, 第1级的OAM分束器参数设为$ (\alpha,\; \delta) $ = (π/4, π), 第2级的两个OAM分束器分别设置为$ (\alpha,\; \delta) $ = (π/8, 3π/2)和$ (\alpha,\; \delta) $ = (π/8, π), 级联后, 有o1o1, o1o2, o2o1和o2o2四个输出端口; (b)级联OAM分束器对OAM态$\left| 1 \right\rangle $, $\left| 2 \right\rangle $, $\left| 7 \right\rangle $和$\left| 8 \right\rangle $分束的实验结果, 图中的百分数表示对某种入射OAM态, 不同端口的输出功率相对于所有端口输出的总功率的比值
Fig. 4. Beam splitting in the cascading case: (a) Cascaded OAM beam splitters. Due to that the OAM states to be separated are $\left| 1 \right\rangle $, $\left| 2 \right\rangle $, $\left| 7 \right\rangle $ and $\left| 8 \right\rangle $, the parameters of the first stage OAM splitter are set as $ (\alpha,\; \delta) $ = (π/4, π), and the two OAM splitters of the second stage are set as $ (\alpha,\; \delta) $ = (π/8, 3π/2) and $ (\alpha,\; \delta) $ = (π/8, π), respectively, after cascading, there are four output ports, o1o1, o1o2, o2o1, and o2o2; (b) experimental results of cascading OAM beam splitters for OAM states $\left| 1 \right\rangle $, $\left| 2 \right\rangle $, $\left| 7 \right\rangle $ and $\left| 8 \right\rangle $, each percentage represents the ratio of each output power to the total output power of all ports for a certain incident OAM state.
-
[1] Coullet P, Gil L, Rocca F 1989 Opt. Commun. 73 403
Google Scholar
[2] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[3] Li S M, Kong L J, Ren Z C, Li Y, Tu C, Wang H T 2013 Phys. Rev. A 88 035801
Google Scholar
[4] Neshev D N, Alexander T J, Ostrovskaya E A, Kivshar Y S, Martin H, Makasyuk I, Chen Z 2004 Phys. Rev. Lett. 92 123903
Google Scholar
[5] Swartzlander G A, Law C T 1992 Phys. Rev. Lett. 69 2503
Google Scholar
[6] Tikhonenko V, Christou J, Luther-Daves B 1995 J. Opt. Soc. Am. B 12 2046
Google Scholar
[7] Firth W J, Skryabin D V 1997 Phys. Rev. Lett. 79 2450
Google Scholar
[8] Dholakia K, Simpson N B, Padgett M J, Allen L 1996 Phys. Rev. A 54 R3742
Google Scholar
[9] Courtial J, Dholakia K, Allen L, Padgett M J 1997 Phys. Rev. A 56 4193
Google Scholar
[10] Andersen M F, Ryu C, Cladé P, Natarajan V, Vaziri A, Helmerson K, Phillips W D 2006 Phys. Rev. Lett. 97 170406
Google Scholar
[11] Grier D G 2003 Nature 424 810
Google Scholar
[12] Paterson L, MacDonald M P, Arlt J, Sibbett W, Bryant P E, Dholakia K 2001 Science 292 912
Google Scholar
[13] Kong L J, Qian S X, Ren Z C, Wang X L, Wang H T 2012 Phys. Rev. A 85 035804
Google Scholar
[14] Dennis M R, King R P, Jack B, O’Holleran K, Padgett M J 2010 Nat. Phys. 6 118
Google Scholar
[15] Larocque H, Sugic D, Mortimer D, Taylor A J, Fickler R, Boyd R W, Dennis M R, Karimi E 2018 Nat. Phys. 14 1079
Google Scholar
[16] Wang L, Zhang W X, Yin H X, Zhang X D 2019 Adv. Opt. Mater. 7 1900263
Google Scholar
[17] Kong L J, Zhang W, Li P, Guo X, Zhang J, Zhang F, Zhao J, Zhang X 2022 Nat. Commun. 13 2705
Google Scholar
[18] Fürhapter S, Jesacher A, Bernet S, Ritsch-Marte M 2005 Opt. Express 13 689
Google Scholar
[19] Kozawa Y, Matsunaga D, Sato S 2018 Optica 5 86
Google Scholar
[20] Fang X, Ren H, Gu M 2020 Nat. Photonics 14 102
Google Scholar
[21] Kong L J, Sun Y, Zhang F, Zhang J, Zhang X 2023 Phys. Rev. Lett. 130 053602
Google Scholar
[22] Zhuang X 2004 Science 305 188
Google Scholar
[23] Berkhout G C G, Beijersbergen M W 2008 Phys. Rev. Lett. 101 100801
Google Scholar
[24] Ke Z J, Wang Y T, Yu S, Liu W, Meng Y, Li Z P, Wang H, Li Q, Xu J S, Xiao Y, Tang J S, Li C F, Guo G C 2020 Chin. Phys. B 29 080301
Google Scholar
[25] Friese M E J, Nieminen T A, Heckenberg N R, Rubinsztein-Dunlop H 1998 Nature 394 348
Google Scholar
[26] Friese M E J, Enger J, Rubinsztein-Dunlop H, Heckenberg N R 1996 Phys. Rev. A 54 1593
Google Scholar
[27] Simpson N B, Dholakia K, Allen L, Padgett M J 1997 Opt. Lett. 22 52
Google Scholar
[28] Bialynicki-Birula I, Bialynicka-Birula Z 1997 Phys. Rev. Lett. 78 2539
Google Scholar
[29] Courtial J, Dholakia K, Robertson D A, Allen L, Padgett M J 1998 Phys. Rev. Lett. 80 3217
Google Scholar
[30] Courtial J, Robertson D A, Dholakia K, Allen L, Padgett M J 1998 Phys. Rev. Lett. 81 4828
Google Scholar
[31] Lavery M P J, Speirits F C, Barnett S M, Padgett M J 2013 Science 341 537
Google Scholar
[32] Wang J, Yang J Y, Fazal I M, Ahmed N, Yan Y, Huang H, Ren Y, Yue Y, Dolinar S, Tur M, Willner A E 2012 Nat. Photonics 6 488
Google Scholar
[33] Huang H, Xie G, Yan Y, Ahmed N, Ren Y, Yue Y, Rogawski D, Willner M J, Erkmen B I, Birnbaum K M, Dolinar S J, Lavery M P J, Padgett M J, Tur M, Willner A E 2014 Opt. Lett. 39 197
Google Scholar
[34] Krenn M, Handsteiner J, Fink M, Fickler R, Ursin R, Malik M, Zeilinger A 2016 Proc. Natl. Acad. Sci. 113 13648
Google Scholar
[35] Watkins R J, Dai K, White G, Li W, Miller J K, Morgan K S, Johnson E G 2020 Opt. Express 28 924
Google Scholar
[36] Bozinovic N, Yue Y, Ren Y, Tur M, Kristensen P, Huang H, Willner A E, Ramachandran S 2013 Science 340 1545
Google Scholar
[37] Mair A, Vaziri A, Weihs G, Zeilinger A 2001 Nature 412 313
Google Scholar
[38] Kong L J, Li Y, Liu R, Qi W R, Wang Q, Wang Z X, Huang S Y, Si Y, Tu C, Hu W, Xu F, Lu Y Q, Wang H T 2019 Phys. Rev. A 100 023822
Google Scholar
[39] Kong L J, Liu R, Qi W R, Wang Z X, Huang S Y, Wang Q, Tu C, Li Y, Wang H T 2019 Sci. Adv. 5 eaat9206
Google Scholar
[40] Romero J, Giovannini D, Franke-Arnold S, Barnett S M, Padgett M J 2012 Phys. Rev. A 86 012334
Google Scholar
[41] Vaziri A, Weihs G, Zeilinger A 2002 Phys. Rev. Lett. 89 240401
Google Scholar
[42] Kong L J, Liu R, Qi W R, Wang Z X, Huang S Y, Tu C, Li Y, Wang H T 2020 Chin. Phys. Lett. 37 034204
Google Scholar
[43] Zhang Y, Agnew M, Roger T, Roux F S, Konrad T, Faccio D, Leach J, Forbes A 2017 Nat. Commun. 8 632
Google Scholar
[44] Dada A C, Leach J, Buller G S, Padgett M J, Andersson E 2011 Nat. Phys. 7 677
Google Scholar
[45] Berkhout G C G, Lavery M P J, Courtial J, Beijersbergen M W, Padgett M J 2010 Phys. Rev. Lett. 105 153601
Google Scholar
[46] Wan C, Chen J, Zhan Q 2017 APL Photonics 2 031302
Google Scholar
[47] Wen Y, Chremmos I, Chen Y, Zhu J, Zhang Y, Yu S 2018 Phys. Rev. Lett. 120 193904
Google Scholar
[48] Malik M, Erhard M, Huber M, Krenn M, Fickler R, Zeilinger A 2016 Nat. Photonics 10 248
Google Scholar
[49] Wang F, Erhard M, Babazadeh A, Malik M, Krenn M, Zeilinger A 2017 Optica 4 1462
Google Scholar
[50] Babazadeh A, Erhard M, Wang F, Malik M, Nouroozi R, Krenn M, Zeilinger A 2017 Phys. Rev. Lett. 119 180510
Google Scholar
[51] Wang X L, Luo Y H, Huang H L, Chen M C, Su Z E, Liu C, Chen C, Li W, Fang Y Q, Jiang X, Zhang J, Li L, Liu N L, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 260502
Google Scholar
[52] Cao H, Gao S C, Zhang C, Wang J, He D Y, Liu B H, Zhou Z W, Chen Y J, Li Z H, Yu S Y, Romero J, Huang Y F, Li C F, Guo G C 2020 Optica 7 232
Google Scholar
[53] Leach J, Padgett M J, Barnett S M, Franke-Arnold S, Courtial J 2002 Phys. Rev. Lett. 88 257901
Google Scholar
[54] Wang F X, Chen W, Yin Z Q, Wang S, Guo G C, Han Z F 2016 Phys. Rev. A 94 033847
Google Scholar
[55] Zhang W, Qi Q, Zhou J, Chen L 2014 Phys. Rev. Lett. 112 153601
Google Scholar
[56] Xue P, Zhang R, Bian Z, Zhan X, Qin H, Sanders B C 2015 Phys. Rev. A 92 042316
Google Scholar
[57] Guo P, Wang S 2022 Photonics 10 1
Google Scholar
[58] Narushima T, Okamoto H 2016 Sci. Rep. 6 35731
Google Scholar
[59] Li P, Guo X, Qi S, Han L, Zhang Y, Liu S, Li Y, Zhao J 2018 Sci. Rep. 8 9831
Google Scholar
[60] Chi Y, Yu Y, Gong Q, Wang J 2023 Sci. China Inf. Sci. 66 180501
Google Scholar
[61] Lei T, Zhang M, Li Y R, Jia P, Liu G N, Xu X G, Li Z H, Min C J, Lin J, Yu C Y, Niu H B, Yuan X C 2015 Light Sci. Appl. 4 e257
Google Scholar
下载:
计量
- 文章访问数: 1848
- PDF下载量: 93
- 被引次数: 0
