-
霍尔管是模拟量子霍尔效应的重要模型, 却至今没有在超导量子电路中实现过. 超导量子电路是宏观调控量子效应的优秀平台. 本文利用超导量子电路系统的高度可调性, 在超导量子电路系统中设计出了具有周期性边界条件的三条超导比特链. 之后利用交流微波对每个比特分别进行驱动, 构造出人造霍尔管. 人造霍尔管中的人造规范场可以通过选择合适的微波相位来进行独立调控. 发现了人造霍尔管中存在不同特征的手性流, 分别为Meissner流和不同面上的涡旋流. 为了判别这些流的存在, 定义了四个序参量, 并在参数空间中画出了不同流之间量子相变的完整相图. 最后, 提出了制备人造霍尔管基态以及探测基态手性流的可行性实验方案. 这一研究丰富了霍尔管的量子流, 并且在已有的实验系统中能够很快实现, 为探索新的量子相提供了新的途径.Hall tube is an important model to simulate the quantum Hall effect. However it hasn't been realized in superconducting circuits which have emerged as a promising platform for macro-controlling quantum effect. Taking advantage of the fine tunability of superconducting circuits, the three-chain superconducting transmon qubits with periodic boundary condition are designed in this paper. For constructing a synthetic Hall tube, ac magnetic fluxes are introduced to drive each transmon qubit. The gauge field emerged in this synthetic Hall tube can be tuned independently by properly choosing the driving phases. Then the ground-state chiral currents are discovered in this synthetic Hall tube, which are Meissner current on
$xy$ plane ($xy$ -M), vortex current on$xy$ plane ($xy$ -V), vortex current on$xz$ plane ($xz$ -V), and vortex current on both$xy$ and$xz$ planes (DV). For distinguishing these chiral currents, four order parameters$J_{C//}$ ,$J_{AB}$ ($J_{BC}$ ), and$J_{CA}$ are defined. Then the ground-state quantum phase diagrams are mapped out. The emergence of the different quantum phases is due to the competition between the coupling strengths$\tilde{t}$ and$t_{CA}$ . The Meissner and vortex currents emerging in this synthetic Hall tube also emerge in type II superconductor, which can generate an opposite field to weaken the influence of the applied field. Thus this synthetic Hall tube can be used as a diamagnet. At last we consider the influence of the imperfections in device fabrication. We proof when the strength of the imperfection is not large enough, the quantum phase diagrams shown in this paper remain valid. Moreover, the possible experimental observations of the ground-state chiral currents are addressed. The ground state of this synthetic Hall tube can be generated by applying microwave pulses. Then the corresponding density matrix can be constructed by the quantum state tomography. After constructing the density matrix, the order parameters can be obtained by calculating the trace. These results enrich the quantum currents in Hall tube and provide a new route to explore novel quantum phases.-
Keywords:
- synthetic Hall tube /
- superconducting circuits /
- chiral currents
[1] Tai M E, Lukin A, Rispoli M, Menke T, Borgnia D, Preiss P M, Grusdt F, Kaufman A M, Greiner M 2017 Nature 546 519
Google Scholar
[2] 刘彪, 周晓凡, 陈刚, 贾锁堂 2020 69 080501
Google Scholar
Liu B, Zhou X F, Chen G, Jia S T 2020 Acta Phys. Sin. 69 080501
Google Scholar
[3] Creutz M 1999 Phys. Rev. Lett. 83 2636
Google Scholar
[4] Hung J S C, Busnaina J H, Chang C W S, Vadiraj A M, Nsanzineza I, Solano E, Alaeian H, Rico E, Wilson C M 2020 Phys. Rev. Lett. 127 100503
Google Scholar
[5] Mancini M, Pagano G, Cappellini G, Livi L, Rider M, Catani J, Sias C, Zoller P, Inguscio M, Dalmonte M, Fallani L 2015 Science 349 1510
Google Scholar
[6] Stuhl B K, Lu H I, Aycock L M, Genkina D, Spielman I B 2015 Science 349 1514
Google Scholar
[7] 夏世强, 唐莉勤, 夏士齐, 马继娜, 燕文超, 宋道红, 胡毅, 许京军, 陈志刚 2020 69 154207
Google Scholar
Xia S Q, Tang L Q, Xia S Q, Ma J N, Yan W C, Song D H, Hu Y, Xu J J, Chen Z G 2020 Acta Phys. Sin. 69 154207
Google Scholar
[8] Hofstadter D R 1976 Phys. Rev. B 14 2239
Google Scholar
[9] Laughlin R B 1981 Phys. Rev. B 23 5632
Google Scholar
[10] Zeng T S, Wang C, Zhai H 2015 Phys. Rev. Lett. 115 095302
Google Scholar
[11] Taddia L, Cornfeld E, Rossini D, Mazza L, Sela E, Fazio R 2017 Phys. Rev. Lett. 118 230402
Google Scholar
[12] Han J H, Kang J H, Shin Y 2019 Phys. Rev. Lett. 122 065303
Google Scholar
[13] Luo X W, Zhang J, Zhang C W 2020 Phys. Rev. A 102 063327
Google Scholar
[14] Zhou X F, Chen G, Jia S T 2020 Phys. Rev. A 102 043313
Google Scholar
[15] Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623
Google Scholar
[16] Gu X, Kockum A F, Miranowicz A, Liu Y, Nori F 2017 Phys. Rep. 718 1
Google Scholar
[17] 喻祥敏, 谭新生, 于海峰, 于扬 2018 67 220302
Google Scholar
Yu X M, Tan X S, Yu H F, Yu Y 2018 Acta Phys. Sin. 67 220302
Google Scholar
[18] 赵士平, 刘玉玺, 郑东宁 2018 67 228501
Google Scholar
Zhao S P, Liu Y X, Zheng D N, 2018 Acta Phys. Sin. 67 228501
Google Scholar
[19] Xu K, Sun Z H, Liu W, Zhang Y R, Li H K, Dong H, Ren W H, Zhang P F, Nori F, Zheng D N, Fan H, Wang H 2020 Sci. Adv. 6 eaba4935
Google Scholar
[20] Xu K, Chen J J, Zeng Y, Zhang Y R, Song C, Liu W X, Guo Q J, Zhang P F, Xu D, Deng H, Huang K Q, Wang H, Zhu X B, Zheng D N, Fan H 2018 Phys. Rev. Lett. 120 050507
Google Scholar
[21] Salathé Y, Mondal M, Oppliger M, Heinsoo J, Kurpiers P, Potočnik A, Mezzacapo A, Heras U L, Lamata L, Solano E, Filipp S, Wallraff A 2015 Phys. Rev. X 5 021027
Google Scholar
[22] Kandala A, Mezzacapo A, Temme K, Takita M, Brink M, Chow J M, Gambetta J M 2017 Nature 549 242
Google Scholar
[23] Cai W, Han J, Mei F, Xu Y, Ma Y, Li X, Wang H, Song Y P, Xue Z Y, Yin Z Q, Jia S T, Sun L Y 2019 Phys. Rev. Lett. 123 080501
Google Scholar
[24] Tan X S, Zhang D W, Yang Z, Chu J, Zhu Y Q, Li D Y, Yang X P, Song S Q, Han Z K, Li Z Y, Dong Y Q, Yu H F, Yan H, Zhu S L, Yu Y 2019 Phys. Rev. Lett. 123 159902
Google Scholar
[25] Yan Z G, Zhang Y R, Gong M, Wu Y L, Zheng Y R, Li S W, Wang C, Liang F T, Lin J, Lin Y, Guo C, Sun L H, Peng C Z, Xia K Y, Deng H, Rong H, You J Q, Nori F, Fan H, Zhu X B, Pan J W 2019 Science 364 753
Google Scholar
[26] Ma R, Saxberg B, Owens C, Leung N, Lu Y, Simon J 2019 Nature 566 51
Google Scholar
[27] Gong M, Wang S Y, Zha C, Chen M C, Huang H L, Wu Y L, Zhu Q L, Zhao Y W, Li S W, Guo S J, Qian H R, Ye Y S, Chen F S, Ying C, Yu J L, Fan D J, Wu D C, Su H, Deng H, Rong H, Zhang K L, Cao S R, Lin J, Xu Y, Sun L H, Guo C, Li N, Liang F T, Bastidas V M, Nemoto K, Munro W J, Huo Y H, Lu C Y, Peng C Z, Zhu X B, Pan J W 2021 Science 372 948
Google Scholar
[28] Li X, Cai T, Yan H, Wang Z, Pan X, Ma Y, Cai W, Han J, Hua Z, Han X, Wu Y, Zhang H, Wang H, Song Y, Duan L, Sun L 2020 Phys. Rev. Appl. 14 024070
Google Scholar
[29] Han X Y, Cai T Q, Li X G, Wu Y K, Ma Y W, Ma Y L, Wang J H, Zhang H Y, Song Y P, Duan L M 2020 Phys. Rev. A 102 022619
Google Scholar
[30] Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319
Google Scholar
[31] Ye Y S, Ge Z Y, Wu Y L, Wang S Y, Ming G, Zhang Y R, Zhu Q L, Yang R, Li S W, Liang F T, Lin J, Xu Y, Guo C, Sun L H, Cheng C, Ma N, Meng Z Y, Deng H, Rong H, Lu C Y, Peng C Z, Fan H, Zhu X B, Pan J W 2019 Phys. Rev. Lett. 123 050502
Google Scholar
[32] Li X, Ma Y, Han J, Chen T, Xu Y, Cai W, Wang H, Song Y P, Xue Z Y, Yin Z Q, Sun L Y 2018 Phys. Rev. Appl. 10 054009
Google Scholar
[33] Atala M, Aidelsburger M, Lohse M, Barreiro J T, Paredes B, Bloch I 2014 Nat. Phys. 10 588
Google Scholar
[34] Piraud M, Meisner F H, McCulloch I P, Greschner S, Vekua T, Schollwöck U 2015 Phys. Rev. B 91 140406(R
Google Scholar
[35] Guan X, Feng Y, Xue Z Y, Chen G, Jia S 2020 Phys. Rev. A 102 032610
Google Scholar
[36] Tai M E, Lukin A, Rispoli M, Schittko R, Menke T, Borgnia D, Preiss P M, Grusdt F, Kaufman A M, Greiner M 2017 Nature 546 519
[37] Wang D W, Song C, Feng W, Cai H, Xu D, Deng H, Li H K, Zheng D N, Zhu X B, Wang H, Zhu S Y, Scully M O 2019 Nat. Phys. 15 382
Google Scholar
[38] Santos R A, Huang C W, Gefen Y, Gutman D B 2015 Phys. Rev. B 91 205141
Google Scholar
[39] Jia W, Huang Z H, Wei X, Zhao Q, Liu X J 2019 Phys. Rev. B 99 094520
Google Scholar
[40] Jiang Y F, Jiang H C 2020 Phys. Rev. Lett. 125 157002
Google Scholar
[41] Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O’Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500
Google Scholar
[42] Song C, Xu K, Liu W, Yang C P, Zheng S B, Deng H, Xie Q, Huang K, Guo Q, Zhang L, Zhang P, Xu D, Zheng D, Zhu X, Wang H, Chen Y A, Lu C Y, Han S, Pan J W 2017 Phys. Rev. Lett. 119 180511
Google Scholar
[43] Roushan P, Neill C, Megrant A, Chen Y, Babbush R, Barends R, Campbell B, Chen Z, Chiaro B, Dunsworth A, Fowler A, Jeffrey E, Kelly J, Lucero E, Mutus J, O’Malley P J J, Neeley M, Quintana C, Sank D, Vainsencher A, Wenner J, White T, Kapit E, Neven H, Martinis J 2017 Nat. Phys. 13 146
Google Scholar
-
图 1 人造霍尔管模型 (a) 三条transmon比特链分别标记为A, B, C. 沿着每条链, 最近邻比特之间耦合. 三条链之间, 同一个元胞中的比特两两耦合. 这里所有的耦合器均为电容.
$ Q_{\nu j} $ 表示的是第ν条链上的第j个比特.$ C_{\nu j} $ 和$ E_{\nu j}^{{\rm{J}}} $ 分别是第ν条链上、第j个比特的有效电容和约瑟夫森能.$ C_{\nu ij} $ 是耦合第ν条链上、第i和第j个元比特的电容.$ \{C_{ABj}, C_{BCj}, C_{CAj}\} $ 是耦合第j个元胞中不同链间比特的电容.$ \phi _{\nu j} $ 是第ν条链上、第j个比特的约瑟夫森结的相位. transmon比特的约瑟夫森结由超导量子干涉仪(SQUID)形成,$ E_{\nu j}^{{\rm{J}}0} $ 是SQUID中每个约瑟夫森结的能量. 每个比特都受到外加磁通$ \varPhi_{\nu j}(t) $ 的调制. (b) 人造霍尔管示意图, 在面$ Q_{A(j-1)}Q_{Aj}Q_{Bj}Q_{B(j-1)} $ 和$ Q_{C(j-1)}Q_{Cj}Q_{Bj}Q_{B(j-1)} $ 上积累$ \varphi_0 $ 的相位, 在面$ Q_{A(j-1)}Q_{Aj}Q_{Cj}Q_{C(j-1)} $ 上积累$ 2\varphi_0 $ 的相位. 图中, 红色、黑色和蓝色的实心球分别表示A, B和C链上的比特Fig. 1. Model of the synthetic Hall tube: (a) Three-leg (labeled respectively by A, B, C) superconducting circuits with transmon qubits. Along each leg, the qubits are coupled with their nearestneighbor sites, while they interact with each other between legs at the same unit cell. All couplers are capacitors.
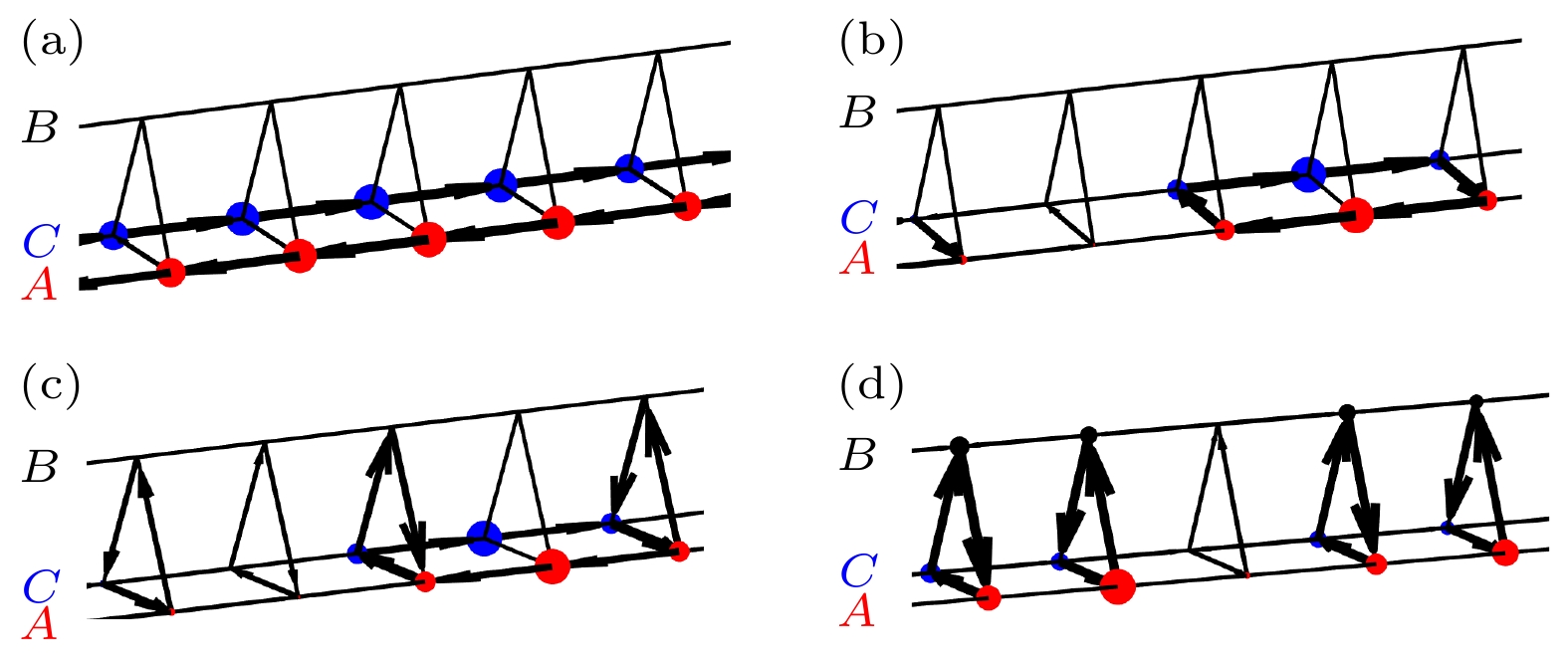
$ C_{\nu j} $ and$ E_{\nu j}^{{\rm{J}}} $ are the effective capacitance and the Josephson energy of the qubit at the j th site on the ν th leg.$ C_{\nu ij} $ and$ \{C_{ABj}, C_{BCj}, C_{CAj}\} $ are the capacitors to couple the qubits at the jth site on the νth leg with its nearest-neighbor sites along each leg and between the legs, respectively.$ \phi _{\nu j} $ is the phase of the Josephson junction of the qubit at the jth site on the νth leg. The Josephson junction of the transmon qubit is a superconducting quantum interference device (SQUID).$ E_{\nu j}^{{\rm{J}}0} $ is the Josephson energy of SQUID. Each qubit is modulate by an external magnetic flux$ \varPhi_{\nu j}(t) $ . (b) Schematics of the synthetic Hall tube with an effective phase$ \varphi_0 $ in the plaquette$ Q_{A(j-1)}Q_{Aj}Q_{Bj}Q_{B(j-1)} $ and$Q_{C(j-1)}Q_{Cj}Q_{Bj} $ $ Q_{B(j-1)}$ and$ 2\varphi_0 $ in the plaquette$ Q_{A(j-1)}Q_{Aj}Q_{Cj}Q_{C(j-1)} $ . The red, black, and blue filled circles indicate the qubits in the A, B and C legs, respectively.
图 2 霍尔管上的流以及比特的态密度分布. 箭头的粗细表示流的强弱, 红色、蓝色和黑色实心小球的大小分别表示A链、B链和C链上比特态密度分布的多少. 参数选择分别为 (a)
$ \tilde{t} = 1.1 $ 和$ t_{CA} = 4.5 $ ; (b)$ \tilde{t} = 0.4 $ 和$ t_{CA} = 1.8 $ ; (c)$ \tilde{t} = 4 $ 和$ t_{CA} = 4.4 $ ; (d)$ \tilde{t} = 2 $ 和$ t_{CA} = 2 $ . 这四个图共同的参数是$ \varphi_0 = 2\pi/3 $ , 并且所有参数均以$ t_0 $ 为单位Fig. 2. Currents and densities distributions on the Hall tube with (a)
$ \tilde{t} = 1.1 $ and$ t_{CA} = 4.5 $ ; (b)$ \tilde{t} = 0.4 $ and$ t_{CA} = 1.8 $ ; (c)$ \tilde{t} = 4 $ and$ t_{CA} = 4.4 $ ; (d)$ \tilde{t} = 2 $ and$ t_{CA} = 2 $ . The thicknesses of the arrow denote the currents strength. The size of the red, black, and blue filled circles indicate the densities on the A, B, and C legs respectively. Here$ t_0 $ is used as the unit. The common parameter is$ \varphi_0 = 2\pi/3 $ .
图 3 参数空间中的相图 (a)
$J_{C//}$ ; (b)$ J_{CA} $ ; (c)$ J_{AB} $ 和$ J_{BC} $ ; (d)参数空间中$ \tilde{t} $ -$ t_{CA} $ 不同的相. 这四个图共同的参数是$ \varphi_0 = 2\pi/3 $ , 并且所有参数均以$ t_0 $ 为单位Fig. 3. Phase diagram of (a)
$J_{C//}$ , (b)$ J_{CA} $ , (c)$ J_{AB} $ and$ J_{BC} $ as functions of$ \tilde{t} $ and$ t_{CA} $ . Different phases are indicated in (d). Here$ t_0 $ is used as the unit. The common parameter is$ \varphi_0 = 2\pi/3 $ .
图 4 不同参数取值下序参量
$J_{C//}$ ,$ J_{AB} $ ,$ J_{BC} $ 和$ J_{CA} $ 随$\lg W$ 的变化 (a)$ \tilde{t} = 1 $ 和$ t_{CA} = 4 $ ; (b)$ \tilde{t} = 0.5 $ 和$ t_{CA} = 2.5 $ ; (c)$ \tilde{t} = 2.5 $ 和$ t_{CA} = 3 $ ; (d)$ \tilde{t} = 2 $ 和$ t_{CA} = 2 $ . 这四个图共同的参数是$ \varphi_0 = 2\pi/3 $ , 并且所有参数均以$ t_0 $ 为单位Fig. 4.
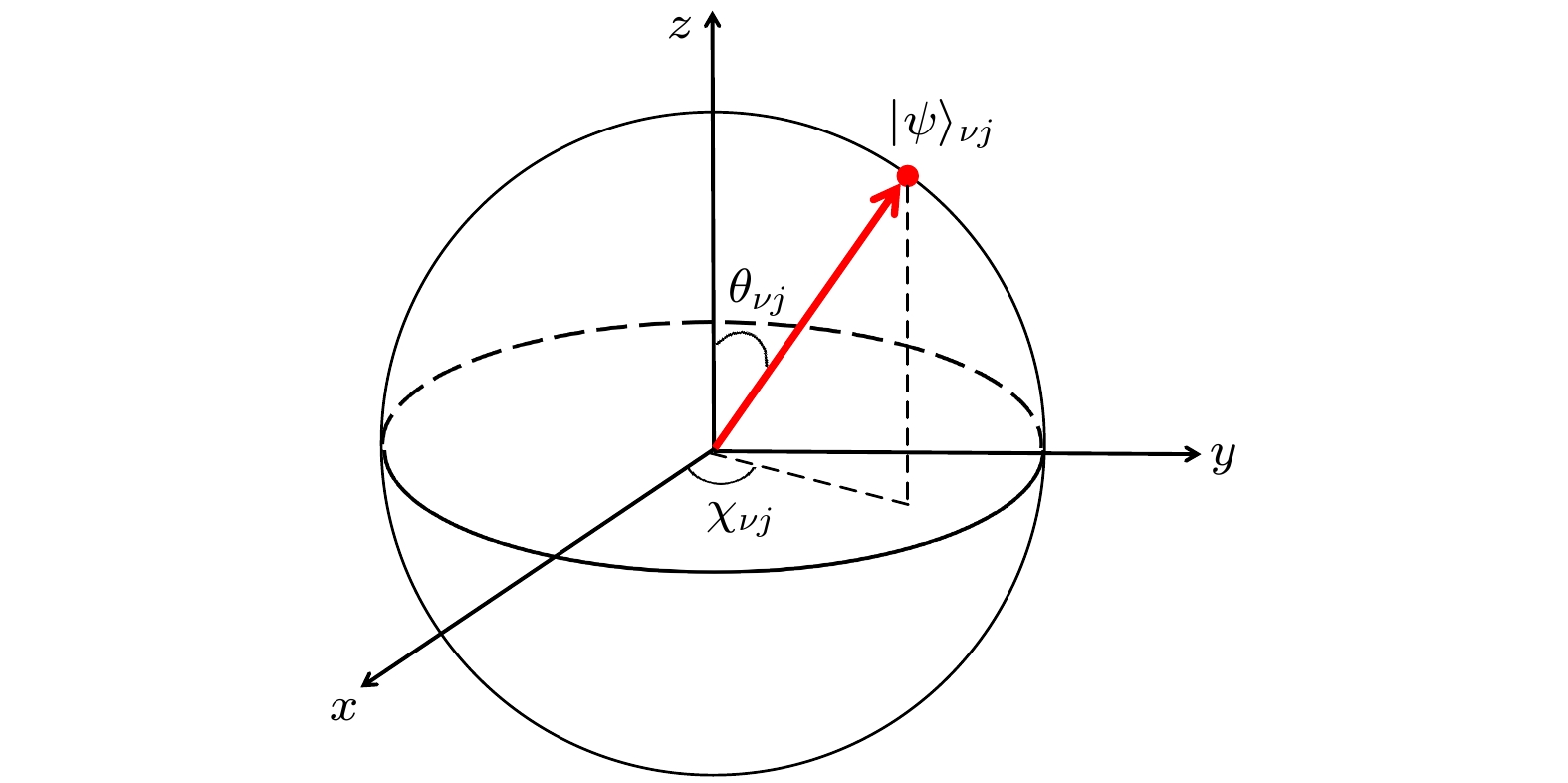
$J_{C//}$ ,$ J_{AB} $ ,$ J_{BC} $ , and$ J_{CA} $ as functions of$\lg W$ with (a)$ \tilde{t} = 1 $ and$ t_{CA} = 4 $ , (b)$ \tilde{t} = 0.5 $ and$ t_{CA} = 2.5 $ ), (c)$ \tilde{t} = 2.5 $ and$ t_{CA} = 3 $ , (d)$ \tilde{t} = 2 $ and$ t_{CA} = 2 $ . The common parameter is$ \varphi_0 = 2\pi/3 $ . Here$ t_0 $ is used as the unit.
图 5 第ν条链的第j个比特的态
$ \vert \psi \rangle _{\nu j} $ 在布洛赫球上的表示.$ \theta _{\nu j} $ 和$ \chi_\nu j $ 分别表示$ \vert \psi \rangle _{\nu j} $ 在布洛赫球上与z轴和x轴的夹角Fig. 5. The jth qubit located on the ν leg described in Bloch sphere.
$ \theta _{\nu j} $ ($ \chi_\nu j $ ) is the angle between the state$ \vert \psi \rangle _{\nu j} $ and z (x) axis in the Bloch sphere.表 1 不同手性流的判别
Table 1. Discriminant of the chiral currents.
手性流的类别 $xy$-M $xy$-V $xz$-V DV $J_{C\Vert }$ 非0 非0 0 非0 $J_{AB }$($J_{BC}$) 0 0 非0 非0 $J_{CA}$ 0 非0 1非0 非0 
下载: 导出CSV
-
[1] Tai M E, Lukin A, Rispoli M, Menke T, Borgnia D, Preiss P M, Grusdt F, Kaufman A M, Greiner M 2017 Nature 546 519
Google Scholar
[2] 刘彪, 周晓凡, 陈刚, 贾锁堂 2020 69 080501
Google Scholar
Liu B, Zhou X F, Chen G, Jia S T 2020 Acta Phys. Sin. 69 080501
Google Scholar
[3] Creutz M 1999 Phys. Rev. Lett. 83 2636
Google Scholar
[4] Hung J S C, Busnaina J H, Chang C W S, Vadiraj A M, Nsanzineza I, Solano E, Alaeian H, Rico E, Wilson C M 2020 Phys. Rev. Lett. 127 100503
Google Scholar
[5] Mancini M, Pagano G, Cappellini G, Livi L, Rider M, Catani J, Sias C, Zoller P, Inguscio M, Dalmonte M, Fallani L 2015 Science 349 1510
Google Scholar
[6] Stuhl B K, Lu H I, Aycock L M, Genkina D, Spielman I B 2015 Science 349 1514
Google Scholar
[7] 夏世强, 唐莉勤, 夏士齐, 马继娜, 燕文超, 宋道红, 胡毅, 许京军, 陈志刚 2020 69 154207
Google Scholar
Xia S Q, Tang L Q, Xia S Q, Ma J N, Yan W C, Song D H, Hu Y, Xu J J, Chen Z G 2020 Acta Phys. Sin. 69 154207
Google Scholar
[8] Hofstadter D R 1976 Phys. Rev. B 14 2239
Google Scholar
[9] Laughlin R B 1981 Phys. Rev. B 23 5632
Google Scholar
[10] Zeng T S, Wang C, Zhai H 2015 Phys. Rev. Lett. 115 095302
Google Scholar
[11] Taddia L, Cornfeld E, Rossini D, Mazza L, Sela E, Fazio R 2017 Phys. Rev. Lett. 118 230402
Google Scholar
[12] Han J H, Kang J H, Shin Y 2019 Phys. Rev. Lett. 122 065303
Google Scholar
[13] Luo X W, Zhang J, Zhang C W 2020 Phys. Rev. A 102 063327
Google Scholar
[14] Zhou X F, Chen G, Jia S T 2020 Phys. Rev. A 102 043313
Google Scholar
[15] Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623
Google Scholar
[16] Gu X, Kockum A F, Miranowicz A, Liu Y, Nori F 2017 Phys. Rep. 718 1
Google Scholar
[17] 喻祥敏, 谭新生, 于海峰, 于扬 2018 67 220302
Google Scholar
Yu X M, Tan X S, Yu H F, Yu Y 2018 Acta Phys. Sin. 67 220302
Google Scholar
[18] 赵士平, 刘玉玺, 郑东宁 2018 67 228501
Google Scholar
Zhao S P, Liu Y X, Zheng D N, 2018 Acta Phys. Sin. 67 228501
Google Scholar
[19] Xu K, Sun Z H, Liu W, Zhang Y R, Li H K, Dong H, Ren W H, Zhang P F, Nori F, Zheng D N, Fan H, Wang H 2020 Sci. Adv. 6 eaba4935
Google Scholar
[20] Xu K, Chen J J, Zeng Y, Zhang Y R, Song C, Liu W X, Guo Q J, Zhang P F, Xu D, Deng H, Huang K Q, Wang H, Zhu X B, Zheng D N, Fan H 2018 Phys. Rev. Lett. 120 050507
Google Scholar
[21] Salathé Y, Mondal M, Oppliger M, Heinsoo J, Kurpiers P, Potočnik A, Mezzacapo A, Heras U L, Lamata L, Solano E, Filipp S, Wallraff A 2015 Phys. Rev. X 5 021027
Google Scholar
[22] Kandala A, Mezzacapo A, Temme K, Takita M, Brink M, Chow J M, Gambetta J M 2017 Nature 549 242
Google Scholar
[23] Cai W, Han J, Mei F, Xu Y, Ma Y, Li X, Wang H, Song Y P, Xue Z Y, Yin Z Q, Jia S T, Sun L Y 2019 Phys. Rev. Lett. 123 080501
Google Scholar
[24] Tan X S, Zhang D W, Yang Z, Chu J, Zhu Y Q, Li D Y, Yang X P, Song S Q, Han Z K, Li Z Y, Dong Y Q, Yu H F, Yan H, Zhu S L, Yu Y 2019 Phys. Rev. Lett. 123 159902
Google Scholar
[25] Yan Z G, Zhang Y R, Gong M, Wu Y L, Zheng Y R, Li S W, Wang C, Liang F T, Lin J, Lin Y, Guo C, Sun L H, Peng C Z, Xia K Y, Deng H, Rong H, You J Q, Nori F, Fan H, Zhu X B, Pan J W 2019 Science 364 753
Google Scholar
[26] Ma R, Saxberg B, Owens C, Leung N, Lu Y, Simon J 2019 Nature 566 51
Google Scholar
[27] Gong M, Wang S Y, Zha C, Chen M C, Huang H L, Wu Y L, Zhu Q L, Zhao Y W, Li S W, Guo S J, Qian H R, Ye Y S, Chen F S, Ying C, Yu J L, Fan D J, Wu D C, Su H, Deng H, Rong H, Zhang K L, Cao S R, Lin J, Xu Y, Sun L H, Guo C, Li N, Liang F T, Bastidas V M, Nemoto K, Munro W J, Huo Y H, Lu C Y, Peng C Z, Zhu X B, Pan J W 2021 Science 372 948
Google Scholar
[28] Li X, Cai T, Yan H, Wang Z, Pan X, Ma Y, Cai W, Han J, Hua Z, Han X, Wu Y, Zhang H, Wang H, Song Y, Duan L, Sun L 2020 Phys. Rev. Appl. 14 024070
Google Scholar
[29] Han X Y, Cai T Q, Li X G, Wu Y K, Ma Y W, Ma Y L, Wang J H, Zhang H Y, Song Y P, Duan L M 2020 Phys. Rev. A 102 022619
Google Scholar
[30] Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319
Google Scholar
[31] Ye Y S, Ge Z Y, Wu Y L, Wang S Y, Ming G, Zhang Y R, Zhu Q L, Yang R, Li S W, Liang F T, Lin J, Xu Y, Guo C, Sun L H, Cheng C, Ma N, Meng Z Y, Deng H, Rong H, Lu C Y, Peng C Z, Fan H, Zhu X B, Pan J W 2019 Phys. Rev. Lett. 123 050502
Google Scholar
[32] Li X, Ma Y, Han J, Chen T, Xu Y, Cai W, Wang H, Song Y P, Xue Z Y, Yin Z Q, Sun L Y 2018 Phys. Rev. Appl. 10 054009
Google Scholar
[33] Atala M, Aidelsburger M, Lohse M, Barreiro J T, Paredes B, Bloch I 2014 Nat. Phys. 10 588
Google Scholar
[34] Piraud M, Meisner F H, McCulloch I P, Greschner S, Vekua T, Schollwöck U 2015 Phys. Rev. B 91 140406(R
Google Scholar
[35] Guan X, Feng Y, Xue Z Y, Chen G, Jia S 2020 Phys. Rev. A 102 032610
Google Scholar
[36] Tai M E, Lukin A, Rispoli M, Schittko R, Menke T, Borgnia D, Preiss P M, Grusdt F, Kaufman A M, Greiner M 2017 Nature 546 519
[37] Wang D W, Song C, Feng W, Cai H, Xu D, Deng H, Li H K, Zheng D N, Zhu X B, Wang H, Zhu S Y, Scully M O 2019 Nat. Phys. 15 382
Google Scholar
[38] Santos R A, Huang C W, Gefen Y, Gutman D B 2015 Phys. Rev. B 91 205141
Google Scholar
[39] Jia W, Huang Z H, Wei X, Zhao Q, Liu X J 2019 Phys. Rev. B 99 094520
Google Scholar
[40] Jiang Y F, Jiang H C 2020 Phys. Rev. Lett. 125 157002
Google Scholar
[41] Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O’Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500
Google Scholar
[42] Song C, Xu K, Liu W, Yang C P, Zheng S B, Deng H, Xie Q, Huang K, Guo Q, Zhang L, Zhang P, Xu D, Zheng D, Zhu X, Wang H, Chen Y A, Lu C Y, Han S, Pan J W 2017 Phys. Rev. Lett. 119 180511
Google Scholar
[43] Roushan P, Neill C, Megrant A, Chen Y, Babbush R, Barends R, Campbell B, Chen Z, Chiaro B, Dunsworth A, Fowler A, Jeffrey E, Kelly J, Lucero E, Mutus J, O’Malley P J J, Neeley M, Quintana C, Sank D, Vainsencher A, Wenner J, White T, Kapit E, Neven H, Martinis J 2017 Nat. Phys. 13 146
Google Scholar
下载:
计量
- 文章访问数: 3713
- PDF下载量: 58
- 被引次数: 0
