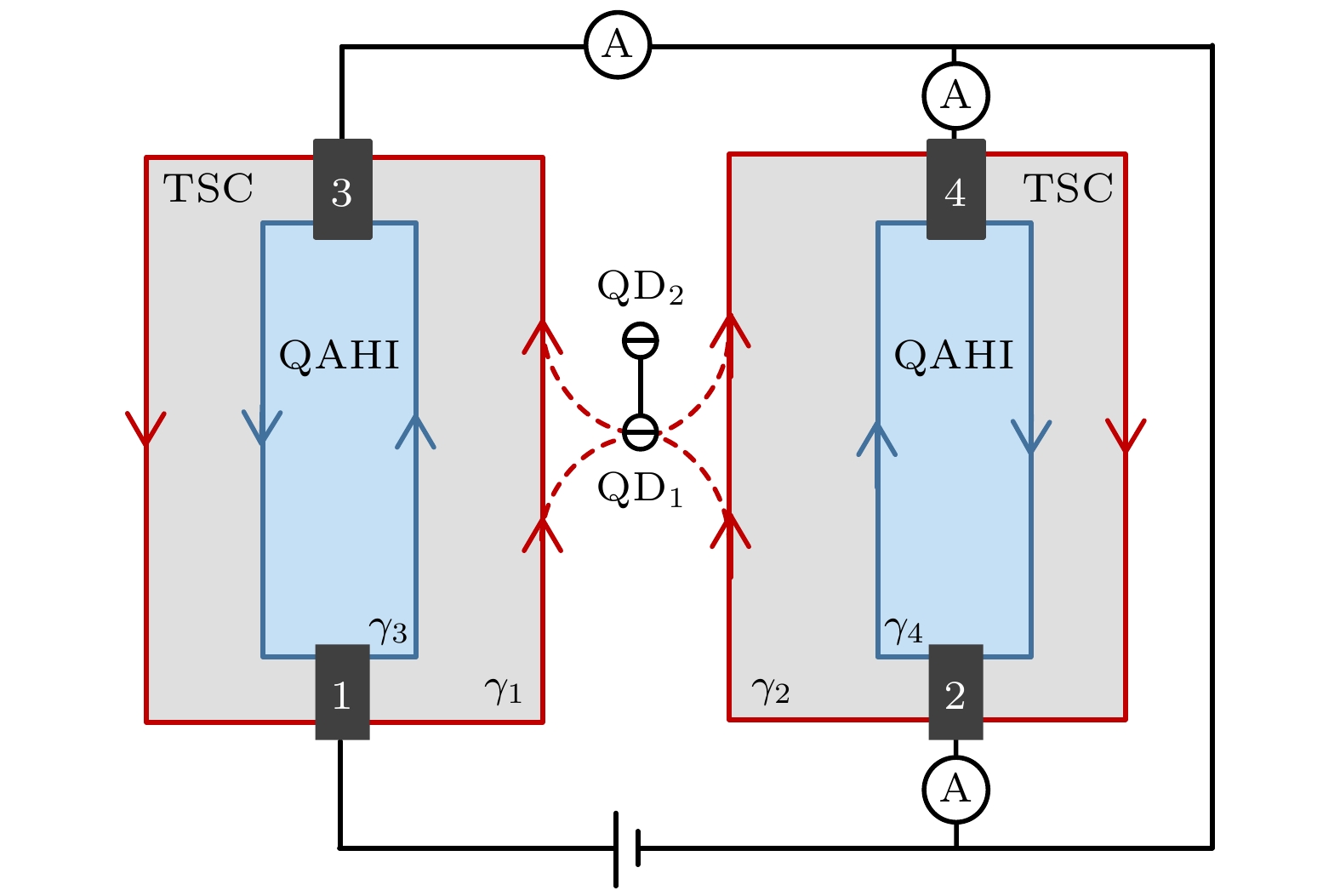
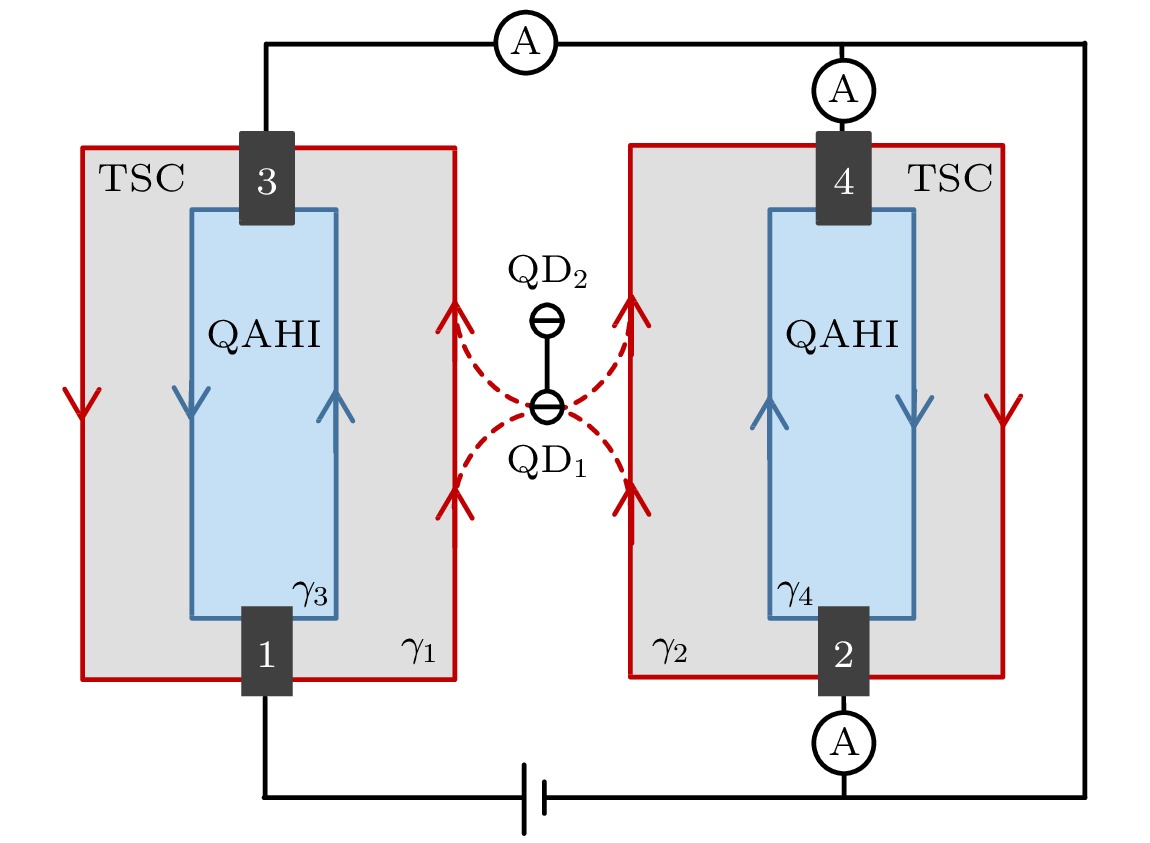
-
本文研究了外部量子点耦合作用下, 量子点耦合两个手性Majorana费米子体系的共振交换. 为了观察两个手性Majorana费米子的共振交换, 提出了一种基于量子反常霍尔绝缘体(QAHI)近邻耦合s波超导体的电路. 数值计算的结果表明, 通过外部量子点耦合强度可以调节手性Majorana费米子的共振透射. 如果经历了共振隧穿的一个手性Majorana费米子与另一个量子点或Majorana零能模发生共振耦合, 则可以实现与超导相位无关的非阿贝尔编织操作. 因此所设计方案为Majorana费米子的非阿贝尔编织操作提供一种新的方式, 这些发现可能在拓扑量子计算的实现中具有潜在的应用价值.
-
关键词:
- 拓扑超导体 /
- 共振隧穿 /
- Majorana费米子 /
- 编织
We study the resonance exchanges of two chiral Majorana fermions in two distinct systems theoretically in this work: one is an isolated Majorana zero mode interacting with complexes formed by two chiral Majorana fermions and a Majorana zero mode, and the other involves isolated quantum dots that are coupled to a system composed of Majorana fermions and a quantum dot. Our research results reveal that both of these coupled systems can facilitate the effective transmissions of the two chiral Majorana fermions as$ {\gamma _1} \to - {\gamma _2} $ and$ {\gamma _2} \to - {\gamma _1} $ , and the resonant tunneling effects in the two systems are equivalent. Therefore, quantum dots can replace Majorana zero modes to achieve resonant tunneling. In order to observe the resonance exchange of two chiral Majorana fermions with the two quantum dots, a circuit based on anomalous quantum Hall insulator proximity-coupled with s-wave superconductor is proposed as shown in figure. The numerical results indicate that the resonant exchange of chiral Majorana fermions can be modulated by the coupling strength between the two quantum dots, and it is particularly noteworthy that the tunneling process is independent of the superconducting phase. If one of the chiral Majorana fermions undergoes resonance coupling with another quantum dot or Majorana zero mode, an additional negative sign is obtained, leading to$ - {\gamma _2} \to {\gamma _1} $ . After experiencing two resonance exchange processes, the final result is$ {\gamma _1} \to {\gamma _2} $ and$ {\gamma _2} \to - {\gamma _1} $ , which implies the realization of non-Abelian braiding operations. Our conclusion is that the modulation of coupling strength between two quantum dots can be used to achieve the switch of Majorana fermions braiding-like operation, which is independent of superconducting phase. Therefore, the designed scheme provides a new way for adjusting the braiding-like operation of Majorana fermions. These findings may have potential applications in the realization of topological quantum computers.
-
Keywords:
- topological superconductor /
- resonant exchange /
- Majorana fermion /
- braiding
[1] Moore G, Read N 1991 Nucl. Phys. B 360 362
Google Scholar
[2] Kitaev A Y 2001 Phys. Usp. 44 131
Google Scholar
[3] Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 6084
Google Scholar
[4] Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602
Google Scholar
[5] Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407
Google Scholar
[6] Qi X L, Hughes T L, Zhang S C 2010 Phys. Rev. B 82 184516
Google Scholar
[7] Wang J, Zhou Q, Lian B, Zhang S C 2015 Phys. Rev. B 92 064520
Google Scholar
[8] Chung S B, Qi X L, Maciejko J, Zhang S C 2011 Phys. Rev. B 83 100512(R
Google Scholar
[9] Wu H B, Zhang Y T, Liu J J 2018 J. Appl. Phys. 124 084301
Google Scholar
[10] Wu H B, Liu J J 2021 Phys. Rev. B 103 115430
Google Scholar
[11] He Q L, Pan L, Stern A L, Burksed E C, Che X Y, Yin G, Wang J, Lian B, Zhou Q, Choi E S, Murata K, Kou X F, Chen Z J, Nie T X, Shao Q M, Fan Y B, Zhang S C, Liu K, Xia J, Wang K L 2017 Science 357 294
Google Scholar
[12] Ji W, Wen X G 2018 Phys. Rev. Lett. 120 107002
Google Scholar
[13] Li Y H, Liu J, Liu H, Jiang H, Sun Q F, Xie X C 2018 Phys. Rev. B 98 045141
Google Scholar
[14] Kayyalha M, Xiao D, Zhang R X, Shin J, Jiang J, Wang F, Zhao Y F, Xiao R, Zhang L, Fijalkowski K M, Mandal P, Winnerlein M, Gould C, Li Q, Molenkamp L W, Chan M H W, Samarth N, Chang C Z 2020 Science 367 64
Google Scholar
[15] 梁奇锋, 王志, 川上拓人, 胡晓 2020 69 117102
Google Scholar
Liang Q F, Wang Z, Kawakami T, Hu X 2020 Acta Phys. Sin. 69 117102
Google Scholar
[16] Alicea J, Oreg Y, Refael G, Oppen F V, Fisher M P A 2011 Nat. Phys. 7 412
Google Scholar
[17] Lian B, Wang J, Sun X Q, Vaezi A, Zhang S C 2018 Phys. Rev. B 97 125408
Google Scholar
[18] Yang N X, Yan Q, Sun Q F 2022 Phys. Rev. B 105 125414
Google Scholar
[19] Beenakker C W J, Baireuther P, Herasymenko Y, Adagideli I, Wang L, Akhmerov A R 2019 Phys. Rev. Lett. 122 146803
Google Scholar
[20] Lian B, Sun X Q, Vaezi A, Qi X L, Zhang S C 2018 Proc. Nat. Acad. Sci. 115 10938
Google Scholar
[21] ZhouY F, Hou Z, Sun Q F 2019 Phys. Rev. B 99 195137
Google Scholar
[22] Yan Q, Sun Q F 2021 Chin. Phys. B 30 040303
Google Scholar
[23] 周洋, 郭健宏 2015 64 167302
Google Scholar
Zhou Y, Guo J H 2015 Acta Phys. Sin. 64 167302
Google Scholar
[24] 王素新, 李玉现, 王宁, 刘建军 2016 65 137302
Google Scholar
Wang S X, Li Y X, Wang N, Liu J J 2016 Acta Phys. Sin. 65 137302
Google Scholar
[25] Majek P, Wójcik K P, Weymann I 2022 Phys. Rev. B 105 075418
Google Scholar
[26] Feng G H, Zhang H H 2022 Phys. Rev. B 105 035148
Google Scholar
[27] Wu H B, Liu Y J, Liu Y D, Liu J J 2024 J. Phys. Condens. Matter 36 345301
Google Scholar
[28] Datta S 1995 Electronic Transport in Mesoscopic System (Cambridge: Cambridge University Press) pp235–240
-
图 1 (a)孤立量子点耦合导线-量子点体系的共振隧穿模型; (b)孤立Majorana零模$ {\gamma _{01}} $耦合两个手性Majorana费米子$ {\gamma _1} $(蓝线) $ {\gamma _2} $(红线)-Majorana零模$ {\gamma _{02}} $复合体系模型; (c)孤立Majorana零模耦合两个手性Majorana费米子-Majorana零模模型实现共振隧穿后再耦合另外一个Majorana零模实现编织模型
Fig. 1. (a) Resonance tunneling model of isolated quantum dot coupled leads-quantum dot system; (b) the isolated Majorana zero mode coupling with two chiral Majorana fermions $ {\gamma _1} $(blue line) $ {\gamma _2} $ (red line) -Majorana zero mode $ {\gamma _{02}} $ system model; (c) isolated Majorana zero mode coupling with two chiral Majorana fermions-Majorana zero mode model to achieve resonance tunneling, followed by coupling with another Majorana zero mode to achieve braiding model.
图 2 孤立量子点耦合量子点-TSC结构的电路示意图
Fig. 2. Circuit diagram of isolated quantum dot (QD2) coupled with quantum dot (QD1)-TSC system.
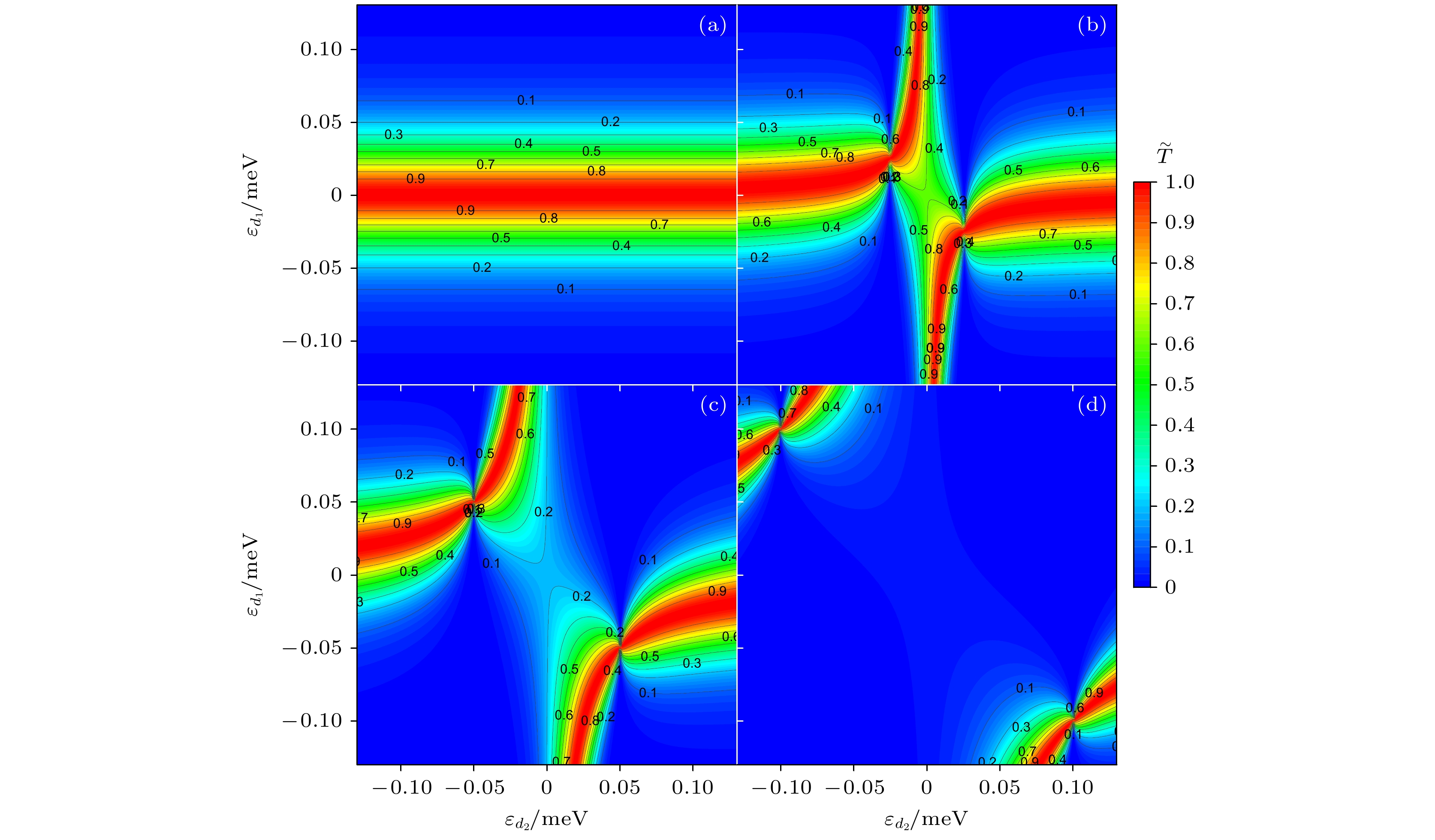
图 3 两个量子点间具有不同的耦合强度下, 有效透射$ \tilde T $与两个量子点能级$ {\varepsilon _{{d_1}}} $和$ {\varepsilon _{{d_2}}} $的函数关系 (a) tdd = 0 meV; (b) tdd = 0.025 meV; (c) tdd = 0.05 meV; (d) tdd = 0.1 meV. 其中$ {\tilde \varGamma _1} = {\tilde \varGamma _2} = 1 \;{\text{meV}} $, 温度为20 mK
Fig. 3. Relationship between effective transmission $ \tilde T $ and the energy levels $ {\varepsilon _{{d_1}}} $ and $ {\varepsilon _{{d_2}}} $ of the two quantum dots with different coupling strengths: (a) tdd = 0 meV; (b) tdd = 0.025 meV; (c) tdd = 0.05 meV; (d) tdd = 0.1 meV. Here $ {\tilde \varGamma _1} = {\tilde \varGamma _2} = 1 \;{\text{meV}} $, the temperature is set to 20 mK.
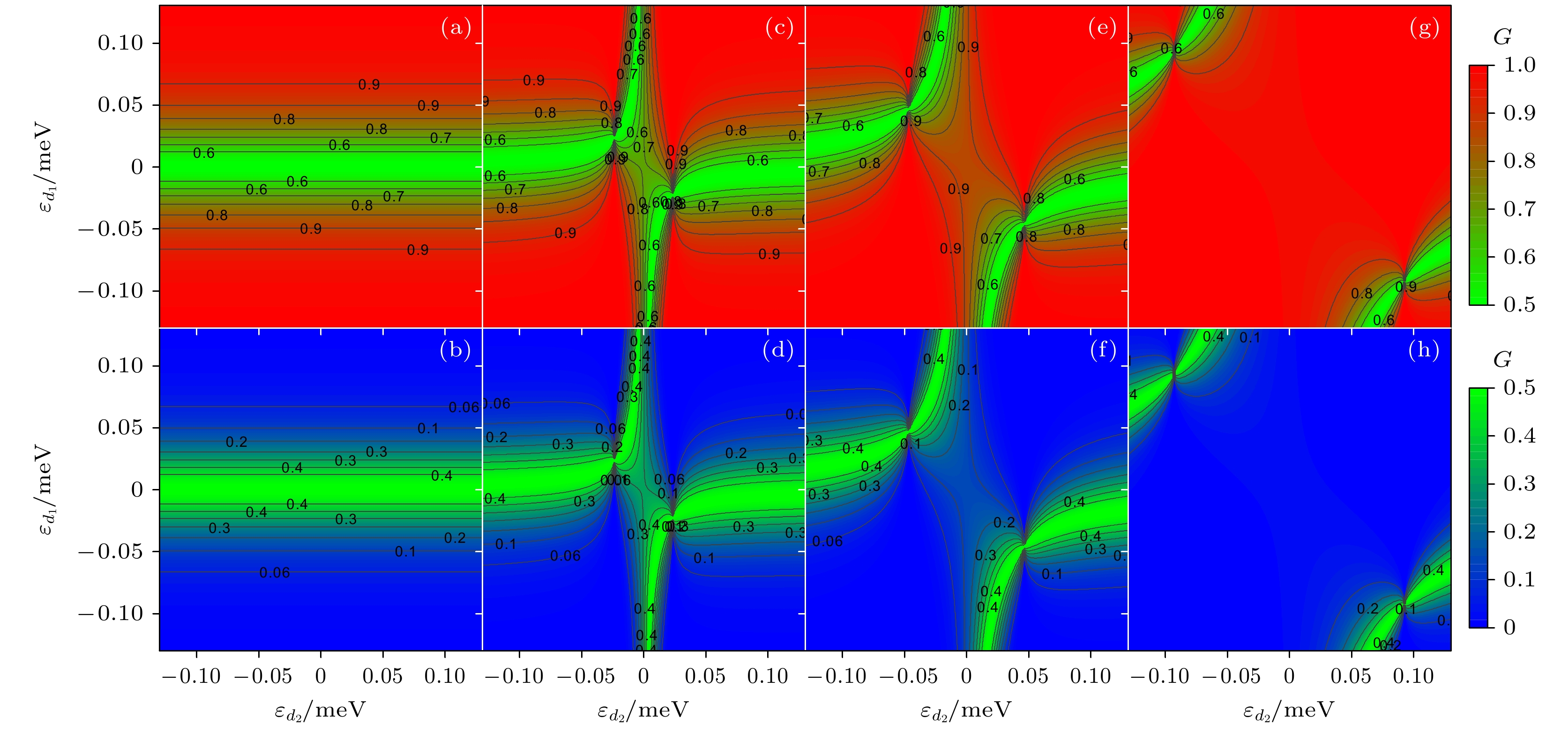
图 4 两个量子点间耦合强度的不同情况下, 电导G与两个量子点能级$ {\varepsilon _{{d_1}}} $和$ {\varepsilon _{{d_2}}} $的函数关系 (a), (b)分别对应于$ {t_{dd}} $= 0 meV的电导G3和G4; (c), (d)分别对应于$ {t_{dd}} $= 0.025 meV的电导G3和G4; (e), (f)分别对应于$ {t_{dd}} $= 0.05 meV的电导G3和G4; (g), (h)分别对应于$ {t_{dd}} $= 0.1 meV的电导G3和G4. 其他参数与图3(a)中使用的参数相同
Fig. 4. Relationship between conductance G and energy levels of two quantum dots $ {\varepsilon _{{d_1}}} $, $ {\varepsilon _{{d_2}}} $at different coupling strengths: (a), (b) Corresponds to conductance G3 and G4 with $ {t_{dd}} $= 0 meV, respectively; (c), (d) corresponds to conductance G3 and G4, respectively, with $ {t_{dd}} $= 0.025 meV; (e), (f) corresponds to conductance G3 and G4 , respectively, with $ {t_{dd}} $=0.05 meV; (g), (h) corresponds to conductance G3 and G4, respectively, with $ {t_{dd}} $= 0.1 meV. Other parameters are the same as those used in Fig.3(a).
-
[1] Moore G, Read N 1991 Nucl. Phys. B 360 362
Google Scholar
[2] Kitaev A Y 2001 Phys. Usp. 44 131
Google Scholar
[3] Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 6084
Google Scholar
[4] Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602
Google Scholar
[5] Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407
Google Scholar
[6] Qi X L, Hughes T L, Zhang S C 2010 Phys. Rev. B 82 184516
Google Scholar
[7] Wang J, Zhou Q, Lian B, Zhang S C 2015 Phys. Rev. B 92 064520
Google Scholar
[8] Chung S B, Qi X L, Maciejko J, Zhang S C 2011 Phys. Rev. B 83 100512(R
Google Scholar
[9] Wu H B, Zhang Y T, Liu J J 2018 J. Appl. Phys. 124 084301
Google Scholar
[10] Wu H B, Liu J J 2021 Phys. Rev. B 103 115430
Google Scholar
[11] He Q L, Pan L, Stern A L, Burksed E C, Che X Y, Yin G, Wang J, Lian B, Zhou Q, Choi E S, Murata K, Kou X F, Chen Z J, Nie T X, Shao Q M, Fan Y B, Zhang S C, Liu K, Xia J, Wang K L 2017 Science 357 294
Google Scholar
[12] Ji W, Wen X G 2018 Phys. Rev. Lett. 120 107002
Google Scholar
[13] Li Y H, Liu J, Liu H, Jiang H, Sun Q F, Xie X C 2018 Phys. Rev. B 98 045141
Google Scholar
[14] Kayyalha M, Xiao D, Zhang R X, Shin J, Jiang J, Wang F, Zhao Y F, Xiao R, Zhang L, Fijalkowski K M, Mandal P, Winnerlein M, Gould C, Li Q, Molenkamp L W, Chan M H W, Samarth N, Chang C Z 2020 Science 367 64
Google Scholar
[15] 梁奇锋, 王志, 川上拓人, 胡晓 2020 69 117102
Google Scholar
Liang Q F, Wang Z, Kawakami T, Hu X 2020 Acta Phys. Sin. 69 117102
Google Scholar
[16] Alicea J, Oreg Y, Refael G, Oppen F V, Fisher M P A 2011 Nat. Phys. 7 412
Google Scholar
[17] Lian B, Wang J, Sun X Q, Vaezi A, Zhang S C 2018 Phys. Rev. B 97 125408
Google Scholar
[18] Yang N X, Yan Q, Sun Q F 2022 Phys. Rev. B 105 125414
Google Scholar
[19] Beenakker C W J, Baireuther P, Herasymenko Y, Adagideli I, Wang L, Akhmerov A R 2019 Phys. Rev. Lett. 122 146803
Google Scholar
[20] Lian B, Sun X Q, Vaezi A, Qi X L, Zhang S C 2018 Proc. Nat. Acad. Sci. 115 10938
Google Scholar
[21] ZhouY F, Hou Z, Sun Q F 2019 Phys. Rev. B 99 195137
Google Scholar
[22] Yan Q, Sun Q F 2021 Chin. Phys. B 30 040303
Google Scholar
[23] 周洋, 郭健宏 2015 64 167302
Google Scholar
Zhou Y, Guo J H 2015 Acta Phys. Sin. 64 167302
Google Scholar
[24] 王素新, 李玉现, 王宁, 刘建军 2016 65 137302
Google Scholar
Wang S X, Li Y X, Wang N, Liu J J 2016 Acta Phys. Sin. 65 137302
Google Scholar
[25] Majek P, Wójcik K P, Weymann I 2022 Phys. Rev. B 105 075418
Google Scholar
[26] Feng G H, Zhang H H 2022 Phys. Rev. B 105 035148
Google Scholar
[27] Wu H B, Liu Y J, Liu Y D, Liu J J 2024 J. Phys. Condens. Matter 36 345301
Google Scholar
[28] Datta S 1995 Electronic Transport in Mesoscopic System (Cambridge: Cambridge University Press) pp235–240
下载:
计量
- 文章访问数: 1531
- PDF下载量: 59
- 被引次数: 0
