基于四波混频过程产生介于锥形探针光和锥形共轭光之间的多模量子关联

曹雷明; 杜金鉴; 张凯; 刘胜帅; 荆杰泰

doi:10.7498/aps.71.20220081

摘要

多模量子关联与纠缠在基础科学研究以及量子信息处理、量子通信等领域有着重要作用. 本文基于热铷原子系综中的四波混频过程, 通过构建具有空间结构的锥形泵浦光和锥形探针光, 在实验上产生具有量子关联的锥形探针光和锥形共轭光, 并测量到量子关联光束之间的强度差压缩约–2.6dB. 通过改变单光子失谐、双光子失谐、泵浦光功率和铷原子池温度等实验参数, 研究量子关联光束之间的强度差噪声随实验参数的变化关系. 除此之外, 通过“整体衰减法”和“局部切割法”对量子关联光束进行不同方式的处理, 不仅实验测量了量子关联随透射率的变化关系, 而且深入研究了量子关联的多模特性. 本文的实验结果在量子信息处理以及量子通信领域有着潜在的应用价值.

关键词:

Abstract

Multimode quantum correlations and entanglements has drawn much attention recently due to its importance for both fundamental science and the future development of quantum information processing and quantum communication. Here, by using a four-wave mixing process with a conical pump beam and a conical probe beam, we experimentally generate the multimode quantum correlations between a conical probe beam and a conical conjugate beam, and we also observe about –2.6-dB intensity-difference squeezing between these two conical beams. In addition, we find the optimal value of each parameter in this scheme for further applications. Besides, the multi-spatial-mode nature of the generated quantum correlated beams is shown by comparing the variation tendencies of the intensity-difference noise of the probe and conjugate beams under global attenuation and local cutting attenuation. Our scheme may find potential applications in quantum information processing and quantum communication.

Keywords:

作者及机构信息

1.
洛阳师范学院物理与电子信息学院, 洛阳　471022

2.
华东师范大学, 精密光谱科学与技术国家重点实验室, 上海　200062

3.
中国科学院超强激光科学卓越创新中心, 上海　201800

4.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 荆杰泰, jtjing@phy.ecnu.edu.cn

基金项目: 上海市教育委员会科研创新计划(批准号: 2021-01-07-00-08-E00100)、国家自然科学基金(批准号: 11874155, 11804141, 91436211, 11374140)、上海市自然科学基金(批准号: 17ZR1442900)、上海市科学技术委员会科技创新行动计划基础研究领域项目(批准号: 20JC1416100)、上海市科技创新行动计划(批准号: 17JC1400401)、上海市市级科技重大专项(批准号: 2019SHZDZX01)、上海市青年科技英才扬帆计划(批准号: 21YF1410800)、闵行领军人才(批准号: 201971)、 111 计划(批准号: B12024)资助的课题

Authors and contacts

1.
Physics and Electronic Information College, Luoyang Normal College, Luoyang 471022, China

2.
State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China

3.
CAS Center for Excellence in Ultra-intense Laser Science, Chinese Academy of Sciences, Shanghai 201800, China

4.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Jing Jie-Tai, jtjing@phy.ecnu.edu.cn

Funds: Project supported by the Innovation Program of Shanghai Municipal Education Commission, China (Grant No. 2021-01-07-00-08-E00100), the National Natural Science Foundation of China (Grant Nos. 11874155, 11804141, 91436211, 11374140), the Natural Science Foundation of Shanghai, China (Grant No. 17ZR1442900), the Basic Research Project of Shanghai Science and Technology Commission, China (Grant No. 20JC1416100), the Program of Scientific and Technological Innovation of Shanghai, China (Grant No. 17JC1400401), the Shanghai Municipal Science and Technology Major Project, China (Grant No. 2019SHZDZX01), the Shanghai Sailing Program, China (Grant No. 21YF1410800), the Minhang Leading Talents, China (Grant No. 201971), and the 111 Project, China (Grant No. B12024).

文章全文 : translate this paragraph

参考文献

[1]	Weedbrook C, Pirandola S, Patrón R G, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621 Google Scholar
[2]	DiVincenzo D P 1995 Science 270 255 Google Scholar
[3]	Lloyd S, Braunstein S L 1999 Phys. Rev. Lett. 82 1784 Google Scholar
[4]	Braunstein S L, van Loock P 2005 Rev. Mod. Phys. 77 513 Google Scholar
[5]	Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Reviews of Modern Physics 84 621
[6]	Jing J T, Zhang J, Yan Y, Zhao F G, Xie C D, Peng K C 2003 Phys. Rev. Lett. 90 167903 Google Scholar
[7]	Yonezawa H, Aoki T, Furasawa A 2004 Nature 431 430 Google Scholar
[8]	van Loock P, Braunstein S L 2000 Phys. Rev. Lett. 84 3482 Google Scholar
[9]	Coelho A S, Barbosa F A S, Cassemiro K N, Villar A S, Martinelli M, Nussenzveig P 2009 Science 326 823 Google Scholar
[10]	Armstrong S, Wang M, Teh R Y, Gong Q, He Q, Janousek J, Bachor H A, Reid M D, Lam P K 2015 Nat. Phys. 11 167 Google Scholar
[11]	Cassemiro K N, Villar A S 2008 Phys. Rev. A 77 022311 Google Scholar
[12]	Su X L, Hao S H, Deng X W, Ma L Y, Wang M H, Jia X J, Xie C D, Peng K C 2013 Nat. Commun. 4 2828 Google Scholar
[13]	Wang X L, Chen L K, Li W, Huang H L, Liu C, Chen C, Luo Y H, Su Z E, Wu D, Li Z D, Lu H, Hu Y, Jiang X, Peng C Z, Li L, Liu N L, Chen Y A, Lu C Y, Pan J W 2016 Phys. Rev. Lett. 117 210502 Google Scholar
[14]	Armstrong S, Wang M, Teh R Y, Gong Q, He Q, Janousek J, Bachor H A, Reid M D, Lam P K 2015 Nature Physics 11 167
[15]	Cassemiro K N, Villar A S 2008 Physical Review A 77 022311
[16]	Yokoyama S, Ukai R, Armstrong S C, Sornphiphatphong C, Kaji T, Suzuki S, Yoshikawa J I, Yonezawa H, Menicucci N C, Furusawa A 2013 Nat. Photonics 7 982 Google Scholar
[17]	Roslund J, De Araújo R M, Jiang S F, Fabre C, Treps N 2014 Nat. Photonics 8 109 Google Scholar
[18]	McCormick C F, Boyer V, Arimondo E, Lett P D 2007 Opt. Lett. 32 178 Google Scholar
[19]	Boyer V, Marino A M, Pooser R C, Lett P D 2008 Science 321 544 Google Scholar
[20]	Marino A M, Pooser R C, Boyer V, Lett P D 2009 Nature 457 859 Google Scholar
[21]	Embrey C S, Turnbull M T, Petrov P G, Boyer V 2015 Phys. Rev. X 5 031004
[22]	Qin Z Z, Cao L M, Wang H L, Marino A M, Zhang W P, Jing J T 2014 Phys. Rev. Lett. 113 023602 Google Scholar
[23]	Cao L M, Qi J, Du J J, Jing J T 2017 Phys. Rev. A 95 023803 Google Scholar
[24]	Liu S S, Wang H L, Jing J T 2018 Phys. Rev. A 97 043846 Google Scholar
[25]	Cao L M, Wang W, Lou Y B, Du J J, Jing J T 2018 Appl. Phys. Lett. 112 251102 Google Scholar
[26]	Wang H L, Zheng Z, Wang Y X, Jing J T 2016 Opt. Express 24 23459 Google Scholar
[27]	Lv S C, Jing J T 2017 Phys. Rev. A 96 043873 Google Scholar
[28]	Chen Y X, Liu S S, Lou Y B, Jing J T 2021 Phys. Rev. Lett. 127 093601 Google Scholar
[29]	Liu S S, Lou Y B, Chen Y X, Jing J T 2021 Phys. Rev. Lett. 126 060503 Google Scholar
[30]	Liu S S, Lou Y B, Jing J T 2020 Nat. Commun. 11 3875 Google Scholar
[31]	Lou Y B, Liu S S, Jing J T 2021 Phys. Rev. Lett. 126 210507 Google Scholar
[32]	Daems D, Bernard F, Cerf N J, Kolobov M I 2010 J. Opt. Soc. Am. B 27 447 Google Scholar
[33]	Daems D, Cerf N J 2010 Phys. Rev. A 82 032303 Google Scholar
[34]	Zhang K, Wang W, Liu S S, Pan X Z, Du J J, Lou Y B, Yu S, Lv S C, Treps N, Fabre C, Jing J T 2020 Phys. Rev. Lett. 124 090501 Google Scholar
[35]	Wang H L, Fabre C, Jing J T 2017 Phys. Rev. A 95 051802 Google Scholar
[36]	Liu S S, Wang H L, Jing J T 2018 Physical Review A 97 043846
[37]	Cao L M, Du J J, Feng J L, Qin Z Z, Marino A M, Kolobov M I, Jing J T 2017 Opt. Lett. 42 1201 Google Scholar
[38]	Marino A M, Boyer V, Pooser R C, Lett P D, Lemons K, Jones K M 2008 Phys. Rev. Lett. 101 093602 Google Scholar

施引文献

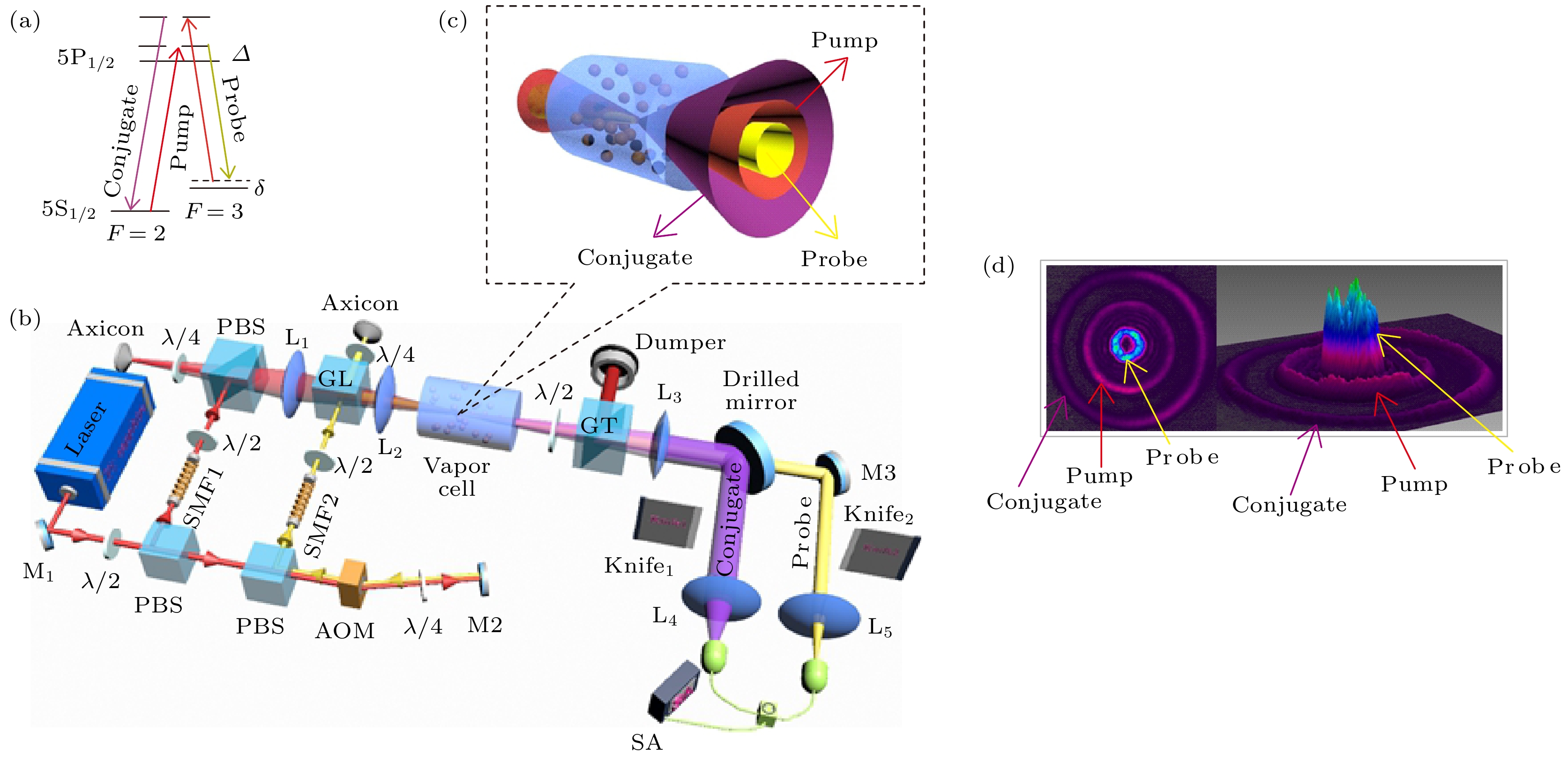
图 1 利用锥形泵浦光和锥形探针光产生和测量多模量子关联的实验系统　(a) 基于铷⁸⁵ 原子D₁线的双“Λ”能级跃迁示意图. Probe是探针光; Conjugate是共轭光; Pump是泵浦光; ∆是单光子失谐; δ是双光子失谐. (b) 实验装置图. M₁—M₃是高反射率的平面反镜; L₁—L₅是透镜; Axicon是锥形棱镜; GL是格兰-激光偏振棱镜; GT是格兰-托马斯棱镜; SA是频谱分析仪; SMF是单模光纤; PBS是偏振光分束器. (c) 锥形泵浦光和锥形探针光通过四波混频反应产生锥形共轭光的示意图. (d) 经四波混频反应后的探针光、共轭光和经过滤后泵浦光在光斑分析仪上呈现的二维和三维图像

Fig. 1. Scheme for generating and detecting multimode quantum correlation: (a) Double-Λ energy level diagram of the ⁸⁵Rb D₁ line. (b) Experimental layout. M₁–M₃, high reflectivity mirrors; L₁–L₅, lenses; Axicon, metal axicon mirror; GL, Glan-Laser polarizer; GT, Glan-Thompson polarizer; SA, spectrum analyzer. (c) Schematic of the conical-pump-based FWM. (d) Two-dimensional and three-dimensional beam pattern captured by a laser beam profiler.

下载: 全尺寸图片幻灯片

图 2 量子关联的实验测量结果　(a) 经四波混频反应后, 归一化的散粒噪声极限SNL (曲线A)、探针光和共轭光的强度差噪声功率(曲线B)、经四波混频放大后的探针光噪声功率(曲线C)、四波混频产生的共轭光的噪声功率(曲线D); (b) 频谱分析仪设置在2 MHz时, 实验测量到的强度差噪声(直线B)和相应的SNL(直线A)随总光功率的变化关系

Fig. 2. Experimental results of quantum correlations: (a) Normalized noise powers of the corresponding SNLs (trace A), intensity-difference noise power between the probe and the conjugate beams (trace B), probe beam (trace C) and conjugate beam (trace D); (b) intensity-difference noise power versus total optical power at 2 MHz. Red line: SNL (trace A), Green line: intensity-difference noise power between the probe and the conjugate (trace B).

下载: 全尺寸图片幻灯片

图 3 实验测量强度差噪声和四波混频的增益随单光子失谐∆、双光子失谐δ、泵浦光功率PP以及铷原子池温度T等实验参数的变化关系

Fig. 3. Dependence of the intensity-difference noise and the power gain on (a) one-photon detuning, (b) two-photon detuning, (c) pump power and (d) temperature in vapor cell. The traces for the intensity-difference noise are plotted in red and the traces for the power gain are plotted in green.

下载: 全尺寸图片幻灯片

图 4 实验测量锥形探针光和锥形共轭光之间量子关联的多模特性　(a) 通过“整体衰减法”和“局部切割法”进行多模特性测量的实验方案示意图. (b) 实验测量的以不同的衰减方式减小功率时, 强度差压缩噪声随透射率的变化关系. 曲线A表示对两束光用半波片和PBS进行整体衰减时, 强度差噪声随透射率的变化关系; 曲线B/C/D分别表示对两束光用薄刀片进行同向、反向和垂直方向的局部切割时, 强度差噪声随透射率的变化关系. (c) 锥形探针光和锥形共轭光之间量子关联的同侧对应关系示意图

Fig. 4. Experimental measurement of multimode quantum correlations between the conical probe and the conical conjugate: (a) The schematic of global attenuation and local attenuation for experimentally measuring multimode quantum correlation. (b) The intensity-difference noise power as a function of the transmittance as the two beams are attenuated equally; Trace A, the two beams are globally attenuated with a variable beam splitter; Trace B/C/D, the two beams are locally attenuated with razor blades cutting from same direction, opposite direction and the perpendicular direction. (c) The schematic of multimode quantum correlations with correspondence on the same side.

下载: 全尺寸图片幻灯片

map

[1]	Weedbrook C, Pirandola S, Patrón R G, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621 Google Scholar
[2]	DiVincenzo D P 1995 Science 270 255 Google Scholar
[3]	Lloyd S, Braunstein S L 1999 Phys. Rev. Lett. 82 1784 Google Scholar
[4]	Braunstein S L, van Loock P 2005 Rev. Mod. Phys. 77 513 Google Scholar
[5]	Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Reviews of Modern Physics 84 621
[6]	Jing J T, Zhang J, Yan Y, Zhao F G, Xie C D, Peng K C 2003 Phys. Rev. Lett. 90 167903 Google Scholar
[7]	Yonezawa H, Aoki T, Furasawa A 2004 Nature 431 430 Google Scholar
[8]	van Loock P, Braunstein S L 2000 Phys. Rev. Lett. 84 3482 Google Scholar
[9]	Coelho A S, Barbosa F A S, Cassemiro K N, Villar A S, Martinelli M, Nussenzveig P 2009 Science 326 823 Google Scholar
[10]	Armstrong S, Wang M, Teh R Y, Gong Q, He Q, Janousek J, Bachor H A, Reid M D, Lam P K 2015 Nat. Phys. 11 167 Google Scholar
[11]	Cassemiro K N, Villar A S 2008 Phys. Rev. A 77 022311 Google Scholar
[12]	Su X L, Hao S H, Deng X W, Ma L Y, Wang M H, Jia X J, Xie C D, Peng K C 2013 Nat. Commun. 4 2828 Google Scholar
[13]	Wang X L, Chen L K, Li W, Huang H L, Liu C, Chen C, Luo Y H, Su Z E, Wu D, Li Z D, Lu H, Hu Y, Jiang X, Peng C Z, Li L, Liu N L, Chen Y A, Lu C Y, Pan J W 2016 Phys. Rev. Lett. 117 210502 Google Scholar
[14]	Armstrong S, Wang M, Teh R Y, Gong Q, He Q, Janousek J, Bachor H A, Reid M D, Lam P K 2015 Nature Physics 11 167
[15]	Cassemiro K N, Villar A S 2008 Physical Review A 77 022311
[16]	Yokoyama S, Ukai R, Armstrong S C, Sornphiphatphong C, Kaji T, Suzuki S, Yoshikawa J I, Yonezawa H, Menicucci N C, Furusawa A 2013 Nat. Photonics 7 982 Google Scholar
[17]	Roslund J, De Araújo R M, Jiang S F, Fabre C, Treps N 2014 Nat. Photonics 8 109 Google Scholar
[18]	McCormick C F, Boyer V, Arimondo E, Lett P D 2007 Opt. Lett. 32 178 Google Scholar
[19]	Boyer V, Marino A M, Pooser R C, Lett P D 2008 Science 321 544 Google Scholar
[20]	Marino A M, Pooser R C, Boyer V, Lett P D 2009 Nature 457 859 Google Scholar
[21]	Embrey C S, Turnbull M T, Petrov P G, Boyer V 2015 Phys. Rev. X 5 031004
[22]	Qin Z Z, Cao L M, Wang H L, Marino A M, Zhang W P, Jing J T 2014 Phys. Rev. Lett. 113 023602 Google Scholar
[23]	Cao L M, Qi J, Du J J, Jing J T 2017 Phys. Rev. A 95 023803 Google Scholar
[24]	Liu S S, Wang H L, Jing J T 2018 Phys. Rev. A 97 043846 Google Scholar
[25]	Cao L M, Wang W, Lou Y B, Du J J, Jing J T 2018 Appl. Phys. Lett. 112 251102 Google Scholar
[26]	Wang H L, Zheng Z, Wang Y X, Jing J T 2016 Opt. Express 24 23459 Google Scholar
[27]	Lv S C, Jing J T 2017 Phys. Rev. A 96 043873 Google Scholar
[28]	Chen Y X, Liu S S, Lou Y B, Jing J T 2021 Phys. Rev. Lett. 127 093601 Google Scholar
[29]	Liu S S, Lou Y B, Chen Y X, Jing J T 2021 Phys. Rev. Lett. 126 060503 Google Scholar
[30]	Liu S S, Lou Y B, Jing J T 2020 Nat. Commun. 11 3875 Google Scholar
[31]	Lou Y B, Liu S S, Jing J T 2021 Phys. Rev. Lett. 126 210507 Google Scholar
[32]	Daems D, Bernard F, Cerf N J, Kolobov M I 2010 J. Opt. Soc. Am. B 27 447 Google Scholar
[33]	Daems D, Cerf N J 2010 Phys. Rev. A 82 032303 Google Scholar
[34]	Zhang K, Wang W, Liu S S, Pan X Z, Du J J, Lou Y B, Yu S, Lv S C, Treps N, Fabre C, Jing J T 2020 Phys. Rev. Lett. 124 090501 Google Scholar
[35]	Wang H L, Fabre C, Jing J T 2017 Phys. Rev. A 95 051802 Google Scholar
[36]	Liu S S, Wang H L, Jing J T 2018 Physical Review A 97 043846
[37]	Cao L M, Du J J, Feng J L, Qin Z Z, Marino A M, Kolobov M I, Jing J T 2017 Opt. Lett. 42 1201 Google Scholar
[38]	Marino A M, Boyer V, Pooser R C, Lett P D, Lemons K, Jones K M 2008 Phys. Rev. Lett. 101 093602 Google Scholar

[1]	盖云冉, 郑康, 丁春玲, 郝向英, 金锐博. 基于半导体量子阱中四波混频效应的高效光学非互易. , 2024, 73(1): 014201. doi: 10.7498/aps.73.20231212
[2]	徐笑吟, 刘胜帅, 荆杰泰. 基于四波混频过程的纠缠光放大. , 2022, 71(5): 050301. doi: 10.7498/aps.71.20211324
[3]	Xiaoyin Xu, shengshuai liu, 荆杰泰. 基于四波混频过程的纠缠光放大. , 2021, (): . doi: 10.7498/aps.70.20211324
[4]	翟淑琴, 康晓兰, 刘奎. 基于级联四波混频过程的量子导引. , 2021, 70(16): 160301. doi: 10.7498/aps.70.20201981
[5]	余胜, 刘焕章, 刘胜帅, 荆杰泰. 基于四波混频过程和线性分束器产生四组份纠缠. , 2020, 69(9): 090303. doi: 10.7498/aps.69.20200040
[6]	仲银银, 潘晓州, 荆杰泰. 级联四波混频相干反馈控制系统量子纠缠特性. , 2020, 69(13): 130301. doi: 10.7498/aps.69.20200042
[7]	万峰, 武保剑, 曹亚敏, 王瑜浩, 文峰, 邱昆. 空频复用光纤中四波混频过程的解析分析方法. , 2019, 68(11): 114207. doi: 10.7498/aps.68.20182129
[8]	杨荣国, 张超霞, 李妮, 张静, 郜江瑞. 级联四波混频系统中纠缠增强的量子操控. , 2019, 68(9): 094205. doi: 10.7498/aps.68.20181837
[9]	曹亚敏, 武保剑, 万峰, 邱昆. 四波混频光相位运算器原理及其噪声性能研究. , 2018, 67(9): 094208. doi: 10.7498/aps.67.20172638
[10]	李述标, 武保剑, 文峰, 韩瑞. 高非线性光纤中四波混频的磁控机理研究. , 2013, 62(2): 024213. doi: 10.7498/aps.62.024213
[11]	李博, 谭中伟, 张晓兴. 利用交叉相位调制和四波混频制作的时间透镜的仿真分析. , 2012, 61(1): 014203. doi: 10.7498/aps.61.014203
[12]	李培丽, 黄德修, 张新亮. 基于PolSK调制的四波混频型超快全光译码器. , 2009, 58(3): 1785-1792. doi: 10.7498/aps.58.1785
[13]	刘霞, 牛金艳, 孙江, 米辛, 姜谦, 吴令安, 傅盘铭. 布里渊增强非简并四波混频. , 2008, 57(8): 4991-4994. doi: 10.7498/aps.57.4991
[14]	苗向蕊, 高士明, 高莹. 基于光纤四波混频效应的新型组播方法. , 2008, 57(12): 7699-7704. doi: 10.7498/aps.57.7699
[15]	杨磊, 李小英, 王宝善. 利用光纤中自发四波混频产生纠缠光子的实验装置. , 2008, 57(8): 4933-4940. doi: 10.7498/aps.57.4933
[16]	邓莉, 孙真荣, 林位株, 文锦辉. 亚10 fs激光脉冲产生中的受激拉曼散射与四波混频效应. , 2008, 57(12): 7668-7673. doi: 10.7498/aps.57.7668
[17]	朱成禹, 吕志伟, 何伟明, 巴德欣, 王雨雷, 高玮, 董永康. 布里渊增强四波混频时域特性的理论研究. , 2007, 56(1): 229-235. doi: 10.7498/aps.56.229
[18]	孙江, 左战春, 郭庆林, 王英龙, 怀素芳, 王颖, 傅盘铭. 应用双光子共振非简并四波混频测量Ba原子里德伯态. , 2006, 55(1): 221-225. doi: 10.7498/aps.55.221
[19]	孙江, 左战春, 米辛, 俞祖和, 吴令安, 傅盘铭. 引入量子干涉的双光子共振非简并四波混频. , 2005, 54(1): 149-154. doi: 10.7498/aps.54.149
[20]	孙　江, 姜　谦, 米　辛, 俞祖和, 傅盘铭. 利用场关联效应抑制瑞利型非简并四波混频的热背底. , 2004, 53(2): 450-455. doi: 10.7498/aps.53.450

计量

文章访问数: 3741
PDF下载量: 96
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于四波混频过程产生介于锥形探针光和锥形共轭光之间的多模量子关联