涂覆石墨烯的嵌套偏心空心圆柱的椭圆形电介质波导的模式特性

李慧慧; 薛文瑞; 李宁; 杜易达; 李昌勇

doi:10.7498/aps.71.20212321

摘要

设计了一种涂覆石墨烯的嵌套偏心空心圆柱的椭圆形电介质纳米线波导. 采用多极方法得到了波导所支持的最低阶的3个模式的传输特性, 即场分布、有效折射率的实部、传播长度和品质因数. 结果显示: 最低阶的3个模式都可由涂覆石墨烯的单根圆柱和椭圆柱所支持的最低阶模式合成. 通过改变波导的结构参数, 即圆柱的半径、椭圆柱半长轴、椭圆柱半短轴及两柱之间的最小间距, 可以在一定程度上调节模式的传输性能. 然而通过增大工作波长、费米能以及减小椭圆形电介质纳米线的介电常数, 可以明显改善模式的传输性能. 文中还与涂覆石墨烯的嵌套偏心空心圆柱的圆形电介质纳米线波导进行比较, 可以发现本文所设计的波导具有更优的传输性能. 这些结果都得到了有限元方法的验证. 本文设计的波导可以为涂覆石墨烯的嵌套偏心空心圆柱的椭圆形电介质纳米线波导的设计、制作及应用提供理论基础.

关键词:

石墨烯 /
纳米线 /
波导 /
多极方法

Abstract

An elliptical dielectric nanowire waveguide with a nested eccentric hollow cylinder is designed, the inner surface and the outer surface of the waveguide are both coated with graphene. The transmission characteristics of the three lowest order modes supported by the waveguide, i.e. the field distribution, the real part of the effective refractive index, the propagation length, and the quality factor, are obtained by multipole method. The results show that the three lowest order modes of the waveguide can be synthesized by the lowest order modes supported by a single cylinder and an elliptic cylinder coated with graphene. With the increase of the radius of the embedded cylinder, the three evaluation indexes of the waveguide increase slightly. The change of the semi major axis of the ellipse will slightly increase the real part of the effective refractive index, propagation length and quality factor of Mode 0 and Mode 1, while Mode2 will slightly decrease. When $a = {{b}} = 170\;{\rm{nm}}$, the performance of the circular nested circular waveguide becomes slightly worse than that of the structure in this paper. With the decrease of the semi minor axis of the ellipse, the real part of the effective refractive index, propagation length and quality factor for each of the three modes increase to a certain extent, and have the greatest impact on Mode 1. When ${{b}} = {{a}} = 190\;{\rm{nm}}$, the transmission performance of the circular nested circular waveguide is not so good as that of the structure in this paper. When the distance between the inner rod and the outer rod on the right side increases, the real part of the effective refractive index for each of the three modes decreases, the propagation length and quality factor of Mode 0 and Mode1 gradually decrease, while the propagation length of Mode 2 increases slightly, and the quality factor is basically unchanged. On the contrary, the mode transmission performance can be significantly improved by increasing the working wavelength and Fermi energy and reducing the dielectric constant of elliptical dielectric nanowires. Compared with the circular dielectric nanowire waveguide nested with an eccentric hollow cylinder coated with graphene, the waveguide designed in this paper can be found to have a good transmission performance. These results are verified by the finite element method. This waveguide can provide a theoretical basis for the design, fabrication and application of nested waveguides of the same type.

Keywords:

作者及机构信息

1.
山西大学物理电子工程学院, 太原　030006

2.
山西大学激光光谱研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

3.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 薛文瑞, wrxue@sxu.edu.cn

基金项目: 国家自然科学基金(批准号: 61378039, 61575115)和国家基础科学人才培养基金(批准号: J1103210)资助的课题.

Authors and contacts

1.
College of Physics and Electronic Engineering, Shanxi University, Taiyuan 030006, China

2.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Laser Spectroscopy, Shanxi University, Taiyuan 030006, China

3.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Xue Wen-Rui, wrxue@sxu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 61378039, 61575115) and the National basic science talents training fund of China (Grant No. J1103210).

文章全文 : translate this paragraph

参考文献

[1]	Maier S A 2007 Plasmonics: fundamentals and applications (New York: Springer) p21
[2]	Yang L K, Li P, Wang H C, Li Z P 2018 Chin. Phys. B 27 094216
[3]	Jablan M, Buljan H, Soljacic M 2009 Phys. Rev. B 80 245435 Google Scholar
[4]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 Google Scholar
[5]	Koppens F H L, Chang D E, de Abajo F J G 2011 Nano Lett. 11 3370
[6]	de Abajo F J G 2014 ACS Photonics 1 135 Google Scholar
[7]	Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109 Google Scholar
[8]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A A 2005 Nature 438 197 Google Scholar
[9]	Geim A K, Novoselov K S 2007 Nat. Mater. 6 183 Google Scholar
[10]	滕达, 王凯, 李哲, 曹清, 唐亚楠, 赵永哲, 刘子怡, 张韵雯, 郭荣珍 2020 光学学报 40 0623002 Google Scholar Teng D, Wang K, Li Z, Cao Q, Tang Y N, Zhao Y Z, Liu Z Y, Zhang Y W, Guo R Z 2020 Acta Opt. Sin. 40 0623002 Google Scholar
[11]	Li Z Q, Henriksen E A, Jiang Z, Hao Z, Martin M C, Kim P, Stormer H L, Basov D N 2008 Nat. Phys. 4 532 Google Scholar
[12]	Teng D, Wang K 2021 Nanomaterials 11 210 Google Scholar
[13]	秦康 2016 硕士学位论文 (浙江: 中国计量大学) Qin K 2016 M. S. Thesis (Zhejiang: China Jiliang University) (in Chinese)
[14]	Wen B, Cao M S, Lu M M, Cao W Q, Shi H L, Liu J, Wang X X, Jin H B, Fang X Y, Wang W Z, Yuan J 2014 Adv. Mater. 26 3484 Google Scholar
[15]	Zhang M, Cao M S, Shu J C, Cao W Q, Li L, Yuan J 2021 Mat. Sci. Eng. R. 145 100627 Google Scholar
[16]	Vakil A, Engheta N 2011 Science 332 1291 Google Scholar
[17]	Gao Y X, Ren G B, Zhu B F, Liu H Q, Lian Y D, Jian S S 2014 Opt. Express 22 24322 Google Scholar
[18]	Yang J F, Yang J J, Deng W, Mao F C, Huang M 2015 Opt. Express 23 32289 Google Scholar
[19]	彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 67 038102 Google Scholar Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Phys. Sin. 67 038102 Google Scholar
[20]	Teng D, Wang K, Li Z, Zhao Y Z, Zhao G, Li H Y, Wang H 2019 Appl. Sci-Basel. 9 2351 Google Scholar
[21]	Cheng X, Xue W R, Wei Z Z, Dong H Y, Li C Y 2019 Opt. Commun. 452 467 Google Scholar
[22]	White T P, Kuhlmey B T, McPhedran R C, Maystre D, Renversez G, Sterke C M, Botten L C 2002 J. Opt. Soc. Am. B 19 2322 Google Scholar
[23]	Bao Q L, Loh K P 2012 ACS Nano 6 3677 Google Scholar
[24]	Bonaccorso F, Sun Z, Hasan T, Ferrari A C 2010 Nat. Photonics 4 611 Google Scholar
[25]	翟利, 薛文瑞, 杨荣草, 韩丽萍 2015 光学学报 35 1123001 Google Scholar Zhai L, Xue W R, Yang R C, Han L P 2015 Acta Opt. Sin. 35 1123001 Google Scholar
[26]	Schedin F, Geim A K, Morozov S V, Hill E W, Blake P, Katsnelson M I, Novoselov K S 2007 Nat. Mater. 6 652 Google Scholar
[27]	Zhang J, Boyd A, Tselev A, Paranjape M, Barbara P 2006 Appl. Phys. Lett. 88 123112 Google Scholar
[28]	郭亚楠, 薛文瑞, 张文梅 2009 58 4168 Google Scholar Guo Y N, Xue W R, Zhang W M 2009 Acta Phys. Sin. 58 4168 Google Scholar
[29]	邓新华, 刘江涛, 袁吉任, 王同标 2015 64 057801 Google Scholar Deng X H, Liu J T, Yuan J R, Wang T B 2015 Acta Phys. Sin. 64 057801 Google Scholar
[30]	Nikitin A Y, Guinea F, Garcia-Vidal F J, Martin-Moreno L 2011 Phys. Rev. B 84 195446 Google Scholar
[31]	Chen K, Zhou X, Cheng X, Qiao R X, Cheng Y, Liu C, Xie Y D, Yu W T, Yao F R, Sun Z P, Wang F, Liu K H, Liu Z F 2019 Nat. Photonics 13 754 Google Scholar
[32]	Erricolo D, Carluccio G 2013 ACM Trans. Math. Soft. 40 153
[33]	Teng D, Wang K, Li Z, Zhao Y Z 2019 Opt. Express 27 12458 Google Scholar
[34]	Xing R, Jian S S 2017 IEEE Photonic Tech. L. 29 1643 Google Scholar
[35]	Ye S, Wang Z X, Sun C R, Dong C B, Wei B Z, Wu B L, Jian S S 2018 Opt. Express 26 23854 Google Scholar

施引文献

图 1 内外表面涂覆石墨烯的内嵌偏心空心圆柱的椭圆形电介质波导的横截面示意图

Fig. 1. The cross section of the waveguide. It was constructed with an elliptical dielectric rod embedded with eccentric hollow cylinder. The inner and outer surfaces of the waveguide were coated with graphene.

下载: 全尺寸图片幻灯片

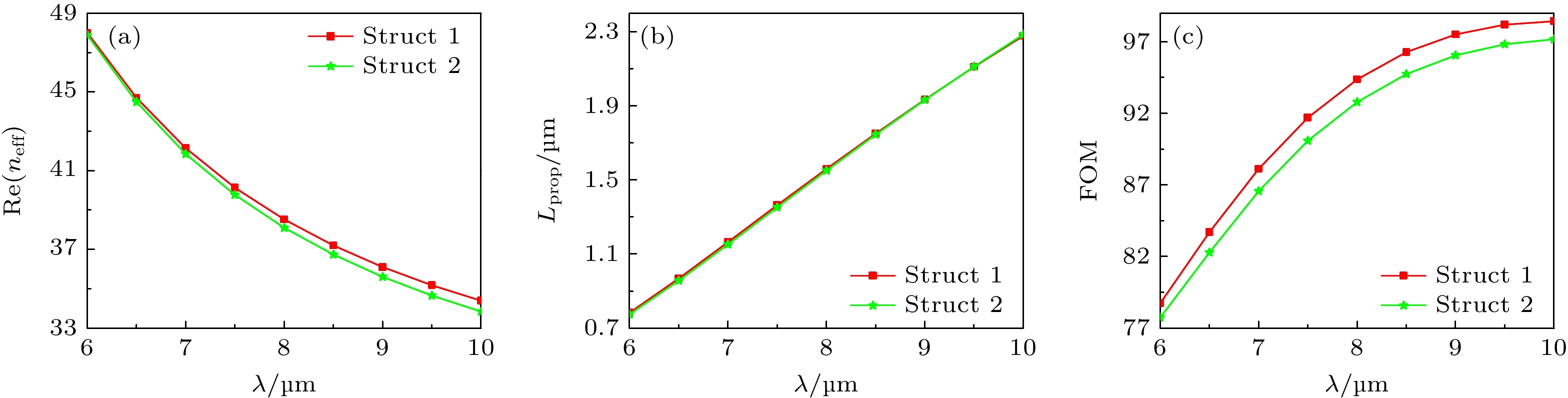
图 2 模式有效折射率实部(a)、传播长度(b)及品质因数(c)随$\lambda $的变化关系图; λ = 6 μm (d), λ = 8 μm (e), λ = 10 μm (f)时Mode0的电场强度分布图

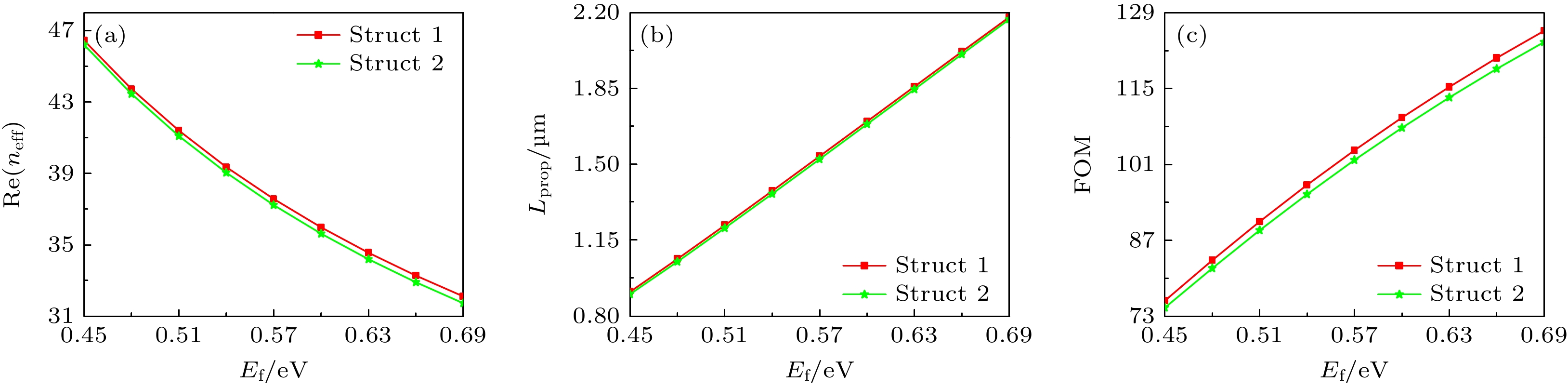
Fig. 2. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) with $\lambda $; the electric field intensity distribution of Mode0 when λ = 6 μm (d), λ = 8 μm (e), λ = 10 μm (f).

下载: 全尺寸图片幻灯片

图 3 有效模式折射率实部(a)、传播长度(b)及品质因数(c)随费米能E_f 的变化关系图; E_f = 0.45 eV(d), E_f = 0.57 eV(e)和E_f = 0.69 eV(f)时Mode0的电场强度分布图

Fig. 3. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) with E_f ; the electric field intensity distribution of Mode0 when E_f = 0.45 eV(d), E_f = 0.57 eV(e) and E_f = 0.69 eV(f).

下载: 全尺寸图片幻灯片

图 4 有效模式折射率实部(a)、传播长度(b)及品质因数(c)随${\rho _0}$的变化关系图; ρ₀ = 60 nm (d), ρ₀ = 80 nm (e), ρ₀ = 100 nm (f)时Mode0的电场强度分布图

Fig. 4. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) with ${\rho _0}$; the electric field intensity distribution of Mode0 when ρ₀ = 60 nm (d), ρ₀ = 80 nm (e), ρ₀ = 100 nm (f).

下载: 全尺寸图片幻灯片

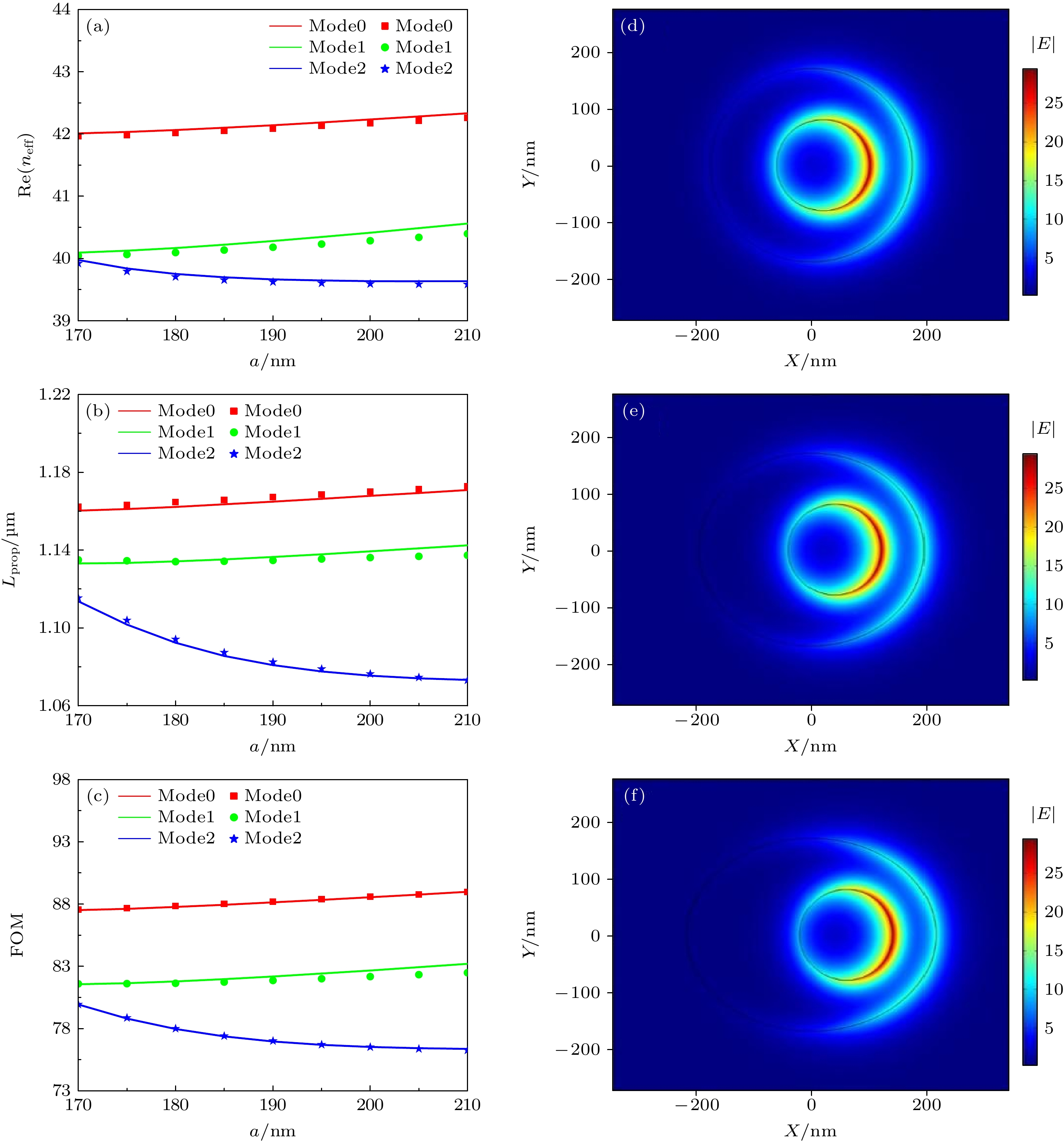
图 5 有效模式折射率实部(a), 传播长度(b)及品质因数(c)随$a$的变化关系图; a = 170 nm (d), a = 190 nm (e), a = 210 nm (f)时Mode0的电场强度分布图

Fig. 5. The variation diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) with $a$; the electric field intensity distribution of Mode0 when a = 170 nm (d), a = 190 nm (e), a = 210 nm (f).

下载: 全尺寸图片幻灯片

图 6 有效模式折射率实部(a), 传播长度(b)及品质因数(c)随$ b $的变化关系图; b = 150 nm (d), b = 170 nm (e), b = 190 nm (f)时Mode0的电场强度分布图

Fig. 6. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) with b; the electric field intensity distribution of Mode0 when b = 150 nm (d)、b = 170 nm (e)、b = 190 nm (f).

下载: 全尺寸图片幻灯片

图 7 有效模式折射率实部(a)、传播长度(b)及品质因数(c)随$d$的变化关系图; d = 55 nm (d), d = 75 nm (e), d = 95 nm (f)时Mode0的电场强度分布图

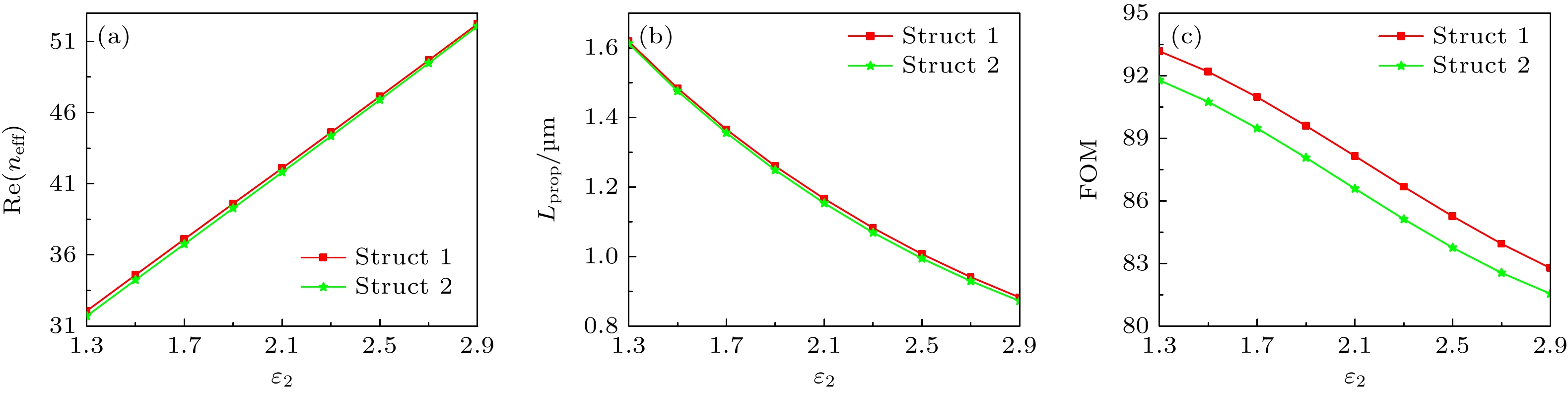
Fig. 7. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) with $d$; the electric field intensity distribution of Mode0 when d = 55 nm (d), d = 75 nm (e), d = 95 nm (f).

下载: 全尺寸图片幻灯片

图 8 有效模式折射率实部(a)、传播长度(b)及品质因数(c)随${\varepsilon _2}$的变化关系图; ${\varepsilon _2} = 1.3$ (d), ${\varepsilon _2} = 2.1$ (e), ${\varepsilon _2} = 2.9$ (f)时Mode0的电场强度分布图

Fig. 8. The variation diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) with ${\varepsilon _2}$; the electric field intensity distribution of Mode0 when ${\varepsilon _2} = 1.3$ (d), ${\varepsilon _2} = 2.1$ (e), ${\varepsilon _2} = 2.9$ (f).

下载: 全尺寸图片幻灯片

图 9 两种结构所支持的基模的有效折射率实部(a)、传播长度(b)和品质因数(c)随波长$\lambda $的变化图

Fig. 9. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) of the fundamental mode supported by the two structures with $\lambda $.

下载: 全尺寸图片幻灯片

图 10 两种结构所支持的基模的有效折射率实部(a)、传播长度(b)和品质因数(c)随E_f变化的关系图

Fig. 10. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) of the fundamental mode supported by the two structures with E_f.

下载: 全尺寸图片幻灯片

图 11 两种结构所支持的基模的有效折射率实部(a)、传播长度(b)和品质因数(c)随${\varepsilon _2}$变化的关系图

Fig. 11. The diagram of the real part of effective refractive index (a), propagation length (b) and FOM (c) of the fundamental mode supported by the two structures with ${\varepsilon _2}$.

下载: 全尺寸图片幻灯片

表 1 波导所支持的3个最低阶模式的模式合成图、${E_z}$分布图及 $|E|$分布图

Table 1. The pattern synthesis diagram, the distribution diagram of ${E_z}$and $|E|$ of the three lowest modes supported by the waveguide.

模式名称模式的合成 ${E_z}$ $|E|$

Mode0
Mode1
Mode2

下载: 导出CSV

map

[1]	Maier S A 2007 Plasmonics: fundamentals and applications (New York: Springer) p21
[2]	Yang L K, Li P, Wang H C, Li Z P 2018 Chin. Phys. B 27 094216
[3]	Jablan M, Buljan H, Soljacic M 2009 Phys. Rev. B 80 245435 Google Scholar
[4]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 Google Scholar
[5]	Koppens F H L, Chang D E, de Abajo F J G 2011 Nano Lett. 11 3370
[6]	de Abajo F J G 2014 ACS Photonics 1 135 Google Scholar
[7]	Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109 Google Scholar
[8]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A A 2005 Nature 438 197 Google Scholar
[9]	Geim A K, Novoselov K S 2007 Nat. Mater. 6 183 Google Scholar
[10]	滕达, 王凯, 李哲, 曹清, 唐亚楠, 赵永哲, 刘子怡, 张韵雯, 郭荣珍 2020 光学学报 40 0623002 Google Scholar Teng D, Wang K, Li Z, Cao Q, Tang Y N, Zhao Y Z, Liu Z Y, Zhang Y W, Guo R Z 2020 Acta Opt. Sin. 40 0623002 Google Scholar
[11]	Li Z Q, Henriksen E A, Jiang Z, Hao Z, Martin M C, Kim P, Stormer H L, Basov D N 2008 Nat. Phys. 4 532 Google Scholar
[12]	Teng D, Wang K 2021 Nanomaterials 11 210 Google Scholar
[13]	秦康 2016 硕士学位论文 (浙江: 中国计量大学) Qin K 2016 M. S. Thesis (Zhejiang: China Jiliang University) (in Chinese)
[14]	Wen B, Cao M S, Lu M M, Cao W Q, Shi H L, Liu J, Wang X X, Jin H B, Fang X Y, Wang W Z, Yuan J 2014 Adv. Mater. 26 3484 Google Scholar
[15]	Zhang M, Cao M S, Shu J C, Cao W Q, Li L, Yuan J 2021 Mat. Sci. Eng. R. 145 100627 Google Scholar
[16]	Vakil A, Engheta N 2011 Science 332 1291 Google Scholar
[17]	Gao Y X, Ren G B, Zhu B F, Liu H Q, Lian Y D, Jian S S 2014 Opt. Express 22 24322 Google Scholar
[18]	Yang J F, Yang J J, Deng W, Mao F C, Huang M 2015 Opt. Express 23 32289 Google Scholar
[19]	彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 67 038102 Google Scholar Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Phys. Sin. 67 038102 Google Scholar
[20]	Teng D, Wang K, Li Z, Zhao Y Z, Zhao G, Li H Y, Wang H 2019 Appl. Sci-Basel. 9 2351 Google Scholar
[21]	Cheng X, Xue W R, Wei Z Z, Dong H Y, Li C Y 2019 Opt. Commun. 452 467 Google Scholar
[22]	White T P, Kuhlmey B T, McPhedran R C, Maystre D, Renversez G, Sterke C M, Botten L C 2002 J. Opt. Soc. Am. B 19 2322 Google Scholar
[23]	Bao Q L, Loh K P 2012 ACS Nano 6 3677 Google Scholar
[24]	Bonaccorso F, Sun Z, Hasan T, Ferrari A C 2010 Nat. Photonics 4 611 Google Scholar
[25]	翟利, 薛文瑞, 杨荣草, 韩丽萍 2015 光学学报 35 1123001 Google Scholar Zhai L, Xue W R, Yang R C, Han L P 2015 Acta Opt. Sin. 35 1123001 Google Scholar
[26]	Schedin F, Geim A K, Morozov S V, Hill E W, Blake P, Katsnelson M I, Novoselov K S 2007 Nat. Mater. 6 652 Google Scholar
[27]	Zhang J, Boyd A, Tselev A, Paranjape M, Barbara P 2006 Appl. Phys. Lett. 88 123112 Google Scholar
[28]	郭亚楠, 薛文瑞, 张文梅 2009 58 4168 Google Scholar Guo Y N, Xue W R, Zhang W M 2009 Acta Phys. Sin. 58 4168 Google Scholar
[29]	邓新华, 刘江涛, 袁吉任, 王同标 2015 64 057801 Google Scholar Deng X H, Liu J T, Yuan J R, Wang T B 2015 Acta Phys. Sin. 64 057801 Google Scholar
[30]	Nikitin A Y, Guinea F, Garcia-Vidal F J, Martin-Moreno L 2011 Phys. Rev. B 84 195446 Google Scholar
[31]	Chen K, Zhou X, Cheng X, Qiao R X, Cheng Y, Liu C, Xie Y D, Yu W T, Yao F R, Sun Z P, Wang F, Liu K H, Liu Z F 2019 Nat. Photonics 13 754 Google Scholar
[32]	Erricolo D, Carluccio G 2013 ACM Trans. Math. Soft. 40 153
[33]	Teng D, Wang K, Li Z, Zhao Y Z 2019 Opt. Express 27 12458 Google Scholar
[34]	Xing R, Jian S S 2017 IEEE Photonic Tech. L. 29 1643 Google Scholar
[35]	Ye S, Wang Z X, Sun C R, Dong C B, Wei B Z, Wu B L, Jian S S 2018 Opt. Express 26 23854 Google Scholar

[1]	段谕, 戴小康, 吴晨晨, 杨晓霞. 可调谐的声学型石墨烯等离激元增强纳米红外光谱. , 2024, 73(13): 138101. doi: 10.7498/aps.73.20240489
[2]	沈艳丽, 史冰融, 吕浩, 张帅一, 王霞. 基于石墨烯的Au纳米颗粒增强染料随机激光. , 2022, 71(3): 034206. doi: 10.7498/aps.71.20211613
[3]	王波云, 朱子豪, 高有康, 曾庆栋, 刘洋, 杜君, 王涛, 余华清. 基于石墨烯纳米条波导边耦合矩形腔的等离子体诱导透明效应. , 2022, 71(2): 024201. doi: 10.7498/aps.71.20211397
[4]	王波云, 朱子豪, 高有康, 曾庆栋, 刘洋, 杜君, 王涛, 余华清. 基于石墨烯纳米条波导边耦合矩形腔的等离子体诱导透明效应研究. , 2021, (): . doi: 10.7498/aps.70.20211397
[5]	董慧莹, 秦晓茹, 薛文瑞, 程鑫, 李宁, 李昌勇. 涂覆石墨烯的非对称椭圆电介质纳米并行线的模式分析. , 2020, 69(23): 238102. doi: 10.7498/aps.69.20201041
[6]	王天会, 李昂, 韩柏. 石墨炔/石墨烯异质结纳米共振隧穿晶体管第一原理研究. , 2019, 68(18): 187102. doi: 10.7498/aps.68.20190859
[7]	陈勇, 李瑞. 纳米尺度硼烯与石墨烯的相互作用. , 2019, 68(18): 186801. doi: 10.7498/aps.68.20190692
[8]	程鑫, 薛文瑞, 卫壮志, 董慧莹, 李昌勇. 涂覆石墨烯的椭圆形电介质纳米线光波导的模式特性分析. , 2019, 68(5): 058101. doi: 10.7498/aps.68.20182090
[9]	陈浩, 张晓霞, 王鸿, 姬月华. 基于磁激元效应的石墨烯-金属纳米结构近红外吸收研究. , 2018, 67(11): 118101. doi: 10.7498/aps.67.20180196
[10]	白清顺, 沈荣琦, 何欣, 刘顺, 张飞虎, 郭永博. 纳米微结构表面与石墨烯薄膜的界面黏附特性研究. , 2018, 67(3): 030201. doi: 10.7498/aps.67.20172153
[11]	冯秋菊, 李芳, 李彤彤, 李昀铮, 石博, 李梦轲, 梁红伟. 外电场辅助化学气相沉积方法制备网格状β-Ga2O3纳米线及其特性研究. , 2018, 67(21): 218101. doi: 10.7498/aps.67.20180805
[12]	卫壮志, 薛文瑞, 彭艳玲, 程鑫, 李昌勇. 基于涂覆石墨烯的三根电介质纳米线的THz波导的模式特性分析. , 2018, 67(10): 108101. doi: 10.7498/aps.67.20180036
[13]	彭艳玲, 薛文瑞, 卫壮志, 李昌勇. 涂覆石墨烯的非对称并行电介质纳米线波导的模式特性分析. , 2018, 67(3): 038102. doi: 10.7498/aps.67.20172016
[14]	李丹, 梁君武, 刘华伟, 张学红, 万强, 张清林, 潘安练. CdS/CdS0.48Se0.52轴向异质结纳米线的非对称光波导及双波长激射. , 2017, 66(6): 064204. doi: 10.7498/aps.66.064204
[15]	顾云风, 吴晓莉, 吴宏章. 三终端非对称夹角石墨烯纳米结的弹道热整流. , 2016, 65(24): 248104. doi: 10.7498/aps.65.248104
[16]	盛世威, 李康, 孔繁敏, 岳庆炀, 庄华伟, 赵佳. 基于石墨烯纳米带的齿形表面等离激元滤波器的研究. , 2015, 64(10): 108402. doi: 10.7498/aps.64.108402
[17]	张保磊, 王家序, 肖科, 李俊阳. 石墨烯-纳米探针相互作用有限元准静态计算. , 2014, 63(15): 154601. doi: 10.7498/aps.63.154601
[18]	陈园园, 邹仁华, 宋钢, 张恺, 于丽, 赵玉芳, 肖井华. 纳米银线波导中表面等离极化波激发和辐射的偏振特性研究. , 2012, 61(24): 247301. doi: 10.7498/aps.61.247301
[19]	岳嵩, 李智, 陈建军, 龚旗煌. 基于耦合介质纳米线的深亚波长局域波导. , 2011, 60(9): 094214. doi: 10.7498/aps.60.094214
[20]	盛峥, 黄思训, 曾国栋. 利用Bayesian-MCMC方法从雷达回波反演海洋波导. , 2009, 58(6): 4335-4341. doi: 10.7498/aps.58.4335

计量

文章访问数: 3880
PDF下载量: 66
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

涂覆石墨烯的嵌套偏心空心圆柱的椭圆形电介质波导的模式特性