石墨炔/石墨烯异质结纳米共振隧穿晶体管第一原理研究

王天会; 李昂; 韩柏

doi:10.7498/aps.68.20190859

摘要

石墨烯和石墨炔的化学相容性表明它们能够以不同形式组合在一起, 从而构建新型超高频纳米晶体管. 通过石墨烯-石墨炔-石墨烯异质结纳米带构建双极器件模拟了两种新型纳米共振隧穿晶体管, 根据基于密度泛函理论的第一原理和非平衡格林函数方法对该晶体管的电子结构和量子输运特性进行了理论计算. 电子透射谱和电流-电压曲线的计算结果证明该晶体管的电流主要来源于共振隧穿跃迁并可由横向栅极电压控制, 因此可用作超高频纳米晶体管.

关键词:

Abstract

Resonant tunneling transistors have received wide attention because of their ability to reduce the complexity of circuits, and promise to be an efficient candidate in ultra-high speed and ultra-high frequency applications. The chemical compatibility between graphene and graphdiyne implies that they can be combined into various configurations to fulfill ultra-high frequency nanotransistor. In the present paper, two novel resonant tunneling transistors based on graphene/graphdiyne/graphene double-heterojunction are theoretically developed to model two new kinds of bipolar devices with two representative graphdiyne nanoribbons. The electronic structures of two pristine graphdiyne nanoribbons are investigated by performing the first-principles calculations with all-electron relativistic numerical-orbit scheme as implemented in Dmol3 code. The electronic transport properties including quantum conductance (transmission spectrum) and electrical current varying with bias-voltage for each of the designed graphdiyne nanoribbon transistors are calculated in combination with non-equilibrium Green function formalism. The calculated electronic transmission and current-voltage characteristics of these transistors demonstrate that the current is dominantly determined by resonant tunneling transition and can be effectively controlled by gate electric field thereby representing the favorable negative-differential-conductivity, which is the qualified attribute of ultra-high frequency nanotransistor. It follows from the I-U_b variations explained by electronic transmission spectra that quantum resonance tunneling can occur in the proposed star-like graphdiyne (SGDY) and net-like graphdiyne (NGDY) nanoribbon transistors, with the resonance condition limited to a narrow bias-voltage range, leading to a characteristic resonant peak in I-U_b curve, which means the strong negative differential conductivity. Under a gate voltage of 4 V, when the bias-voltage rises up to 0.6 V (0.7 V), the Fermi level of source electrode aligns identically to the quantized level of SGDY (NGDY) nanoribbon channel, causing electron resonance tunneling as illustrated by the considerable transmission peak in bias window; once the source Fermi level deviates from the quantized level of SGDY (NGDY) channels at higher bias-voltage, the resonance tunneling transforms into ordinary electron tunneling, which results in the disappearing of the substantial transmission peak in bias window and the rapid declining of current. The designed SGDY and NGDY nanotransistors will achieve high-level negative differential conductivity with the peak-to-valley current ratio approaching to 4.5 and 6.0 respectively, which can be expected to be applied to quantum transmission nanoelectronic devices.

Keywords:

作者及机构信息

1.
吉林大学珠海学院公共基础与应用统计学院, 珠海　519041

2.
哈尔滨理工大学电气与电子工程学院, 工程电介质及其应用教育部重点实验室, 黑龙江省电介质工程重点实验室, 哈尔滨　150080

通信作者: 韩柏, bak_han@sina.com

基金项目: 国家自然科学基金(批准号: 51607048)和黑龙江省普通本科高等学校青年创新人才培养计划 (批准号: UNPYSCT-2016049)资助的课题.

Authors and contacts

1.
School of Disciplinary Basics and Applied Statistics, Zhuhai College of Jilin University, Zhuhai 519041, China

2.
Key Laboratory of Engineering Dielectrics and Its Application, Ministry of Education, Heilongjiang Provincial Key Laboratory of Dielectric Engineering, School of Electrical and Electronic Engineering, Harbin University of Science and Technology, Harbin 150080, China

Corresponding author: Han Bai, bak_han@sina.com

Funds: Projects supported by the National Natural Science Foundation of China (Grant No. 51607048) and the Young Innovative Talent Training Program of Heilongjiang Province Undergraduate Colleges and Universities, China (Grant No. UNPYSCT-2016049).

文章全文 : translate this paragraph

参考文献

[1]	Pi S, Lin P, Xia Q 2016 Nanotechnology 27 464004 Google Scholar
[2]	Lawrence T C, Vashishtha V, Shifren L, Gujja A, Sinha S, Cline B, Ramamurthy C, Yeric G 2016 Microelect. J. 53 105 Google Scholar
[3]	Guo Y G, Wang F Q, Wang Q 2017 Appl. Phys. Lett. 111 073503 Google Scholar
[4]	Punniyakoti S, Sivakumarasamy R, Vaurette F, Joseph P, Nishiguchi K, Fujiwara A, Clement N 2017 Adv. Mater. Interf. 4 1601155 Google Scholar
[5]	Murugesan A 2014 Int. J. Innovative Sci. Eng. Tech. 1 264
[6]	Akbar F, Kolahduz M, Larimian S, Radamson H H 2015 J. Mater. Sci. Mater. Elect. 26 4347 Google Scholar
[7]	Park J S, Choi H J 2015 Phys. Rev. B 92 045402 Google Scholar
[8]	Mihnev M T, Wang F, Liu G, Rothwell S, Cohen P I, Feldman L C, Conrad E H, Norris T B 2015 Appl. Phys. Lett. 107 173107 Google Scholar
[9]	Li G, Li Y, Liu H, Guo Y, Li Y, Zhu D 2010 Chem. Commun. 46 3256 Google Scholar
[10]	Cranford S W, Buehler M J 2011 Carbon 49 4111 Google Scholar
[11]	Kang J, Li J, Wu F, Li S S, Xia J B 2011 J. Phys. Chem. C 115 20466 Google Scholar
[12]	Long M, Tang L, Wang D, Li Y, Shuai Z 2011 ACS Nano 5 2593 Google Scholar
[13]	Zhou J, Lü K, Wang Q, Chen X S, Sun Q, Jena P 2011 J. Chem. Phys. 134 174701 Google Scholar
[14]	Capasso F, Kiehl R A 1985 J. Appl. Phys. 58 1366 Google Scholar
[15]	Teong H, Lam K T, Khalid S B, Liang G 2009 J. Appl. Phys. 105 084317 Google Scholar
[16]	Britnell L, Gorbachev R V, Geim A K, Ponomarenko L A, Mishchenko A, Greenaway M T, Fromhold T M, Novoselov K S, Eaves L 2013 Nat. Commun. 4 1794 Google Scholar
[17]	Mishchenko A, Tu J S, Cao Y, Gorbachev R V, Wallbank J R, Greenaway M T, Morozov V E, Morozov S V, Zhu M J, Wong S L, Withers F, Woods C R, Kim Y J, Watanabe K, Taniguchi T, Vdovin E E, Makarovsky O, Fromhold T M, FaI’ko V I, Geim A K, Eaves L, Novoselov K S 2014 Nat. Nanotech. 9 808 Google Scholar
[18]	Özçelik V O, Durgun E, Ciraci S 2015 J. Phys. Chem. C 119 13248 Google Scholar
[19]	Chowdhury S, Chattaraj S, Biswas D 2015 J. Semicond. 36 044001 Google Scholar
[20]	Allis D G, Prokhorova D, Korter T M 2006 J. Phys. Chem. A 110 1951 Google Scholar
[21]	Niehaus T A, Rohlfing M, Della Sala F, Di Carlo A, Frauenheim T 2005 Phys. Rev. A 71 022508 Google Scholar
[22]	Pecchia A, Penazzi G, Salvucci L, Di Carlo A 2008 New J. Phys. 10 065022 Google Scholar
[23]	Chantis A N, Christensen N E, Svane A, Cardona M 2010 Phys. Rev. B 81 205205 Google Scholar
[24]	Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X L, Burke K 2008 Phys. Rev. Lett. 100 136406 Google Scholar
[25]	Weinert M, Davenport J W 1992 Phys. Rev. B 45 13709 Google Scholar
[26]	Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 Google Scholar
[27]	Tkatchenko A, Scheffler M 2009 Phys. Rev. Lett. 102 073005 Google Scholar
[28]	Ghanbari Shohany B, RoknabadiM R, Kompany A 2016 Commun. Theor. Phys. 65 99 Google Scholar
[29]	Dong J, Li H, Li L 2013 NPG Asia Mater. 5 e56 Google Scholar

施引文献

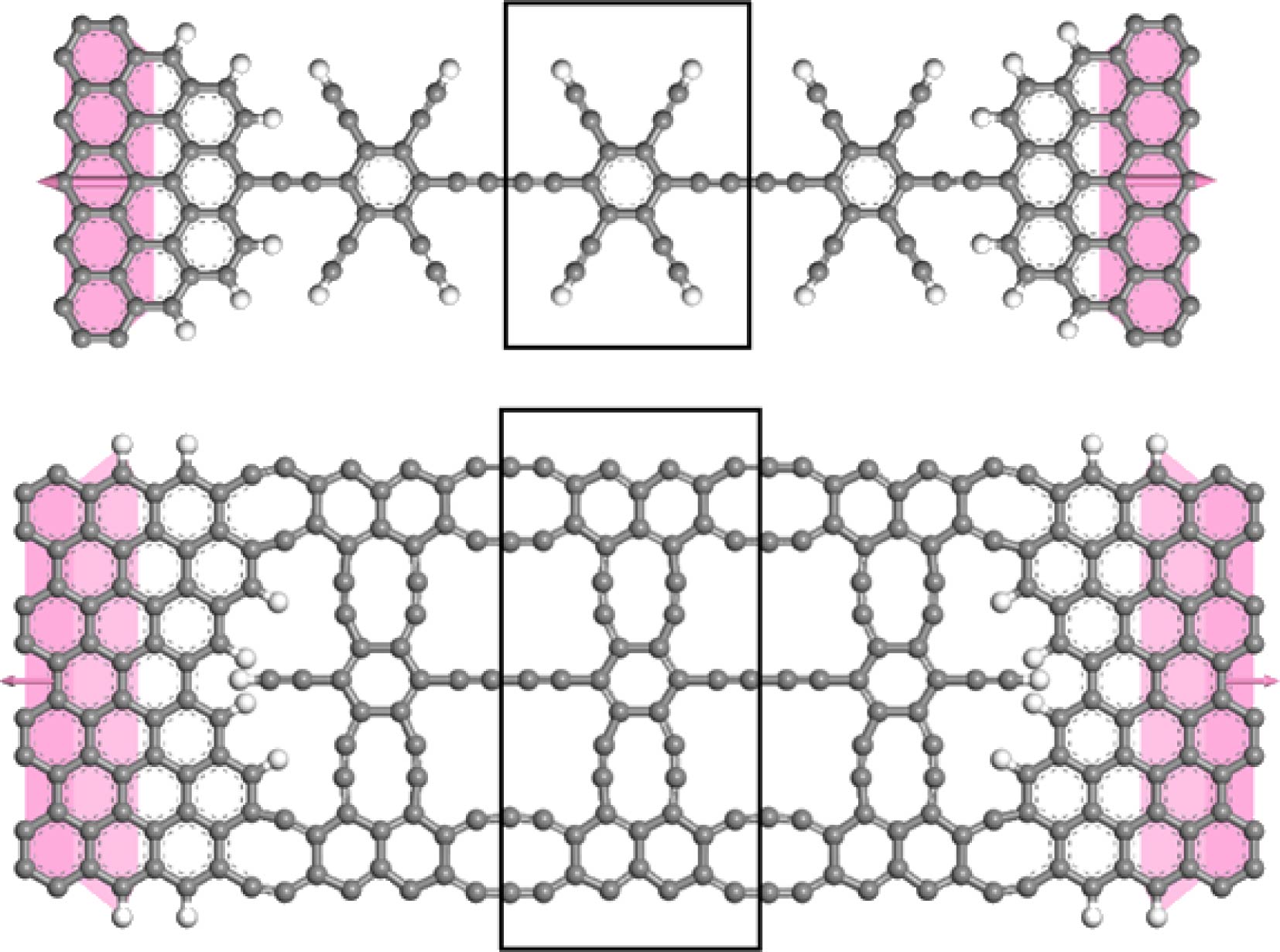
图 1 SGDY (上图)和NGDY (下图)纳米带两端连接石墨烯纳米带半无限电极(源极和漏极粉色区域)构建的双极器件模型, 石墨炔尖端和石墨烯边缘碳原子由氢原子钝化, 黑色框架表示周期性单胞

Fig. 1. Schematic bipolar device models constructed with the SGDY (above panel) or NGDY (below panel) as center scattering region and the graphene nanoribbons as semi-infinite electrodes (source and drain in pink areas). The apex and edge carbon atoms are passivated by hydrogen atoms, and black frames indicate periodic unit cells.

下载: 全尺寸图片幻灯片

图 2 SGDY (a)和NGDY (b)纳米带的电子能带结构, 以费米能级(水平虚线)为能量参考零点

Fig. 2. Electronic energy band structure of SGDY (a) and NGDY (b) nanoribbons with Fermi energy level as reference energy zero (horizontal dashed line).

下载: 全尺寸图片幻灯片

图 3 在SGDY/石墨烯异质结纳米带双极器件的垂直方向施加栅极电压构建的晶体管电子输运计算模型, 粉色区域表示电极, 灰色、白色、红色、黄色和粉色小球分别代表碳、氢、氧、硅和铝原子

Fig. 3. Electron transport calculation in transistor model of bipolar devices with the SGDY/graphene nanoribbons heterostructure as the center scattering region and semi-infinite electrodes (source and drain) respectively under the gate voltage in vertical direction. The pink areas indicate electrodes, and the gray, white, red, yellow and pink spheres represent carbon, hydrogen, oxygen, silicon and aluminium atoms respectively.

下载: 全尺寸图片幻灯片

图 4 SGDY和NGDY纳米带晶体管的漏极电流随偏置电压的变化　(a) U_g = 0 V; (b) U_g = 4 V

Fig. 4. Drain current of SGDY and NGDY nanoribbon transistors varying with bias voltage under (a) U_g = 0 V and (b) U_g = 4 V

下载: 全尺寸图片幻灯片

图 5 SGDY纳米带晶体管在偏置电压0—1.0 V范围内的电子透射谱(栅极电压U_g = 4 V)

Fig. 5. Electron transmission spectra of SGDY nanoribbon transistors in the bias voltage range of 0−1.0 V under gate voltage U_g = 4 V.

下载: 全尺寸图片幻灯片

表 1 使用Dmol3程序的计算方法和参数设置

Table 1. Scheme and parameter setting up in calculationswith Dmol3 program.

电子态描述及求解方法	计算方案	参数设置
交换相关泛函	GGA	PBEsol^[24]
电子与原子实相互作用(core treatment)	全电子相对论(all electron relativistic)
数值基组	双数值极化(DNP)
轨道截至(orbital cutoff)	Global	5.0 Å
SCF	容忍度	1 × 10^–6 Ha/原子 (1 Ha = 27.2 eV)
	多极展开	八极
	密度混合	电荷和自旋混合幅度分别为0.2和0.5
	轨道占据热拖尾(smearing)^[25]	0.001 Ha
布里渊区积分k点取样(电子结构)	Monkhorst-Pack格点^[26]	1 × 1 × 25
计算范德瓦耳斯相互作用	DFT交换-相关泛函色散校正^[27]
布里渊区积分k点取样(电子输运)	均匀间隔格点	间隔0.02/Å
泊松求解法和泊松边界条件(电子输运)	器件侧面缓冲长度	7.5 Å
	泊松网格最大格点间距	0.5 Å
	电极界面边界条件	Dirichlet
	非电极界面边界条件	Neumann
	电极边界区缓冲长度	3 Å

下载: 导出CSV

表 2 不同纳米带晶体管在不同栅极电压下的PVR

Table 2. PVR for nanoribbon transistors fabricated with different materials under different gate voltage.

纳米带散射区	电极	研究方法	栅极电压 /V	PVR	数据来源
SGDY, NGDY	石墨烯	第一原理计算	5	4.5, 6.0	本文
BN	石墨烯	理论计算和实验	0, 20	1—4	Ref. [16]
BN	石墨烯	理论计算和实验	–40, 0, 40	—	Ref. [17]
GaN-Al-GaN	GaN	理论计算(Matlab)	–1, –2, –3	2.66	Ref. [19]

下载: 导出CSV

map

[1]	Pi S, Lin P, Xia Q 2016 Nanotechnology 27 464004 Google Scholar
[2]	Lawrence T C, Vashishtha V, Shifren L, Gujja A, Sinha S, Cline B, Ramamurthy C, Yeric G 2016 Microelect. J. 53 105 Google Scholar
[3]	Guo Y G, Wang F Q, Wang Q 2017 Appl. Phys. Lett. 111 073503 Google Scholar
[4]	Punniyakoti S, Sivakumarasamy R, Vaurette F, Joseph P, Nishiguchi K, Fujiwara A, Clement N 2017 Adv. Mater. Interf. 4 1601155 Google Scholar
[5]	Murugesan A 2014 Int. J. Innovative Sci. Eng. Tech. 1 264
[6]	Akbar F, Kolahduz M, Larimian S, Radamson H H 2015 J. Mater. Sci. Mater. Elect. 26 4347 Google Scholar
[7]	Park J S, Choi H J 2015 Phys. Rev. B 92 045402 Google Scholar
[8]	Mihnev M T, Wang F, Liu G, Rothwell S, Cohen P I, Feldman L C, Conrad E H, Norris T B 2015 Appl. Phys. Lett. 107 173107 Google Scholar
[9]	Li G, Li Y, Liu H, Guo Y, Li Y, Zhu D 2010 Chem. Commun. 46 3256 Google Scholar
[10]	Cranford S W, Buehler M J 2011 Carbon 49 4111 Google Scholar
[11]	Kang J, Li J, Wu F, Li S S, Xia J B 2011 J. Phys. Chem. C 115 20466 Google Scholar
[12]	Long M, Tang L, Wang D, Li Y, Shuai Z 2011 ACS Nano 5 2593 Google Scholar
[13]	Zhou J, Lü K, Wang Q, Chen X S, Sun Q, Jena P 2011 J. Chem. Phys. 134 174701 Google Scholar
[14]	Capasso F, Kiehl R A 1985 J. Appl. Phys. 58 1366 Google Scholar
[15]	Teong H, Lam K T, Khalid S B, Liang G 2009 J. Appl. Phys. 105 084317 Google Scholar
[16]	Britnell L, Gorbachev R V, Geim A K, Ponomarenko L A, Mishchenko A, Greenaway M T, Fromhold T M, Novoselov K S, Eaves L 2013 Nat. Commun. 4 1794 Google Scholar
[17]	Mishchenko A, Tu J S, Cao Y, Gorbachev R V, Wallbank J R, Greenaway M T, Morozov V E, Morozov S V, Zhu M J, Wong S L, Withers F, Woods C R, Kim Y J, Watanabe K, Taniguchi T, Vdovin E E, Makarovsky O, Fromhold T M, FaI’ko V I, Geim A K, Eaves L, Novoselov K S 2014 Nat. Nanotech. 9 808 Google Scholar
[18]	Özçelik V O, Durgun E, Ciraci S 2015 J. Phys. Chem. C 119 13248 Google Scholar
[19]	Chowdhury S, Chattaraj S, Biswas D 2015 J. Semicond. 36 044001 Google Scholar
[20]	Allis D G, Prokhorova D, Korter T M 2006 J. Phys. Chem. A 110 1951 Google Scholar
[21]	Niehaus T A, Rohlfing M, Della Sala F, Di Carlo A, Frauenheim T 2005 Phys. Rev. A 71 022508 Google Scholar
[22]	Pecchia A, Penazzi G, Salvucci L, Di Carlo A 2008 New J. Phys. 10 065022 Google Scholar
[23]	Chantis A N, Christensen N E, Svane A, Cardona M 2010 Phys. Rev. B 81 205205 Google Scholar
[24]	Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X L, Burke K 2008 Phys. Rev. Lett. 100 136406 Google Scholar
[25]	Weinert M, Davenport J W 1992 Phys. Rev. B 45 13709 Google Scholar
[26]	Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 Google Scholar
[27]	Tkatchenko A, Scheffler M 2009 Phys. Rev. Lett. 102 073005 Google Scholar
[28]	Ghanbari Shohany B, RoknabadiM R, Kompany A 2016 Commun. Theor. Phys. 65 99 Google Scholar
[29]	Dong J, Li H, Li L 2013 NPG Asia Mater. 5 e56 Google Scholar

[1]	段谕, 戴小康, 吴晨晨, 杨晓霞. 可调谐的声学型石墨烯等离激元增强纳米红外光谱. , 2024, 73(13): 138101. doi: 10.7498/aps.73.20240489
[2]	沈艳丽, 史冰融, 吕浩, 张帅一, 王霞. 基于石墨烯的Au纳米颗粒增强染料随机激光. , 2022, 71(3): 034206. doi: 10.7498/aps.71.20211613
[3]	徐翔, 张莹, 闫庆, 刘晶晶, 王骏, 徐新龙, 华灯鑫. 不同堆垛结构二硫化铼/石墨烯异质结的光电化学特性. , 2021, 70(9): 098203. doi: 10.7498/aps.70.20201904
[4]	董慧莹, 秦晓茹, 薛文瑞, 程鑫, 李宁, 李昌勇. 涂覆石墨烯的非对称椭圆电介质纳米并行线的模式分析. , 2020, 69(23): 238102. doi: 10.7498/aps.69.20201041
[5]	陈令修, 王慧山, 姜程鑫, 陈晨, 王浩敏. 六方氮化硼表面石墨烯纳米带生长与物性研究. , 2019, 68(16): 168102. doi: 10.7498/aps.68.20191036
[6]	陈勇, 李瑞. 纳米尺度硼烯与石墨烯的相互作用. , 2019, 68(18): 186801. doi: 10.7498/aps.68.20190692
[7]	蔡梦圆, 唐春梅, 张秋月. Li离子电池负极材料石墨炔在B, N掺杂调控下的储Li性能优化. , 2019, 68(21): 213601. doi: 10.7498/aps.68.20191161
[8]	郑加金, 王雅如, 余柯涵, 徐翔星, 盛雪曦, 胡二涛, 韦玮. 基于石墨烯-钙钛矿量子点场效应晶体管的光电探测器. , 2018, 67(11): 118502. doi: 10.7498/aps.67.20180129
[9]	陈浩, 张晓霞, 王鸿, 姬月华. 基于磁激元效应的石墨烯-金属纳米结构近红外吸收研究. , 2018, 67(11): 118101. doi: 10.7498/aps.67.20180196
[10]	白清顺, 沈荣琦, 何欣, 刘顺, 张飞虎, 郭永博. 纳米微结构表面与石墨烯薄膜的界面黏附特性研究. , 2018, 67(3): 030201. doi: 10.7498/aps.67.20172153
[11]	张辉, 蔡晓明, 郝振亮, 阮子林, 卢建臣, 蔡金明. 石墨烯纳米带的制备与电学特性调控. , 2017, 66(21): 218103. doi: 10.7498/aps.66.218103
[12]	张慧珍, 李金涛, 吕文刚, 杨海方, 唐成春, 顾长志, 李俊杰. 石墨烯纳米结构的制备及带隙调控研究. , 2017, 66(21): 217301. doi: 10.7498/aps.66.217301
[13]	谷季唯, 王锦程, 王志军, 李俊杰, 郭灿, 唐赛. 不同衬底条件下石墨烯结构形核过程的晶体相场法研究. , 2017, 66(21): 216101. doi: 10.7498/aps.66.216101
[14]	陈献, 程梅娟, 吴顺情, 朱梓忠. 石墨炔衍生物结构稳定性和电子结构的第一性原理研究. , 2017, 66(10): 107102. doi: 10.7498/aps.66.107102
[15]	迟宝倩, 刘轶, 徐京城, 秦绪明, 孙辰, 白晟灏, 刘一璠, 赵新洛, 李小武. 石墨炔衍生物结构稳定性及电子结构的密度泛函理论研究. , 2016, 65(13): 133101. doi: 10.7498/aps.65.133101
[16]	杨晶晶, 李俊杰, 邓伟, 程骋, 黄铭. 单层石墨烯带传输模式及其对气体分子振动谱的传感特性研究. , 2015, 64(19): 198102. doi: 10.7498/aps.64.198102
[17]	盛世威, 李康, 孔繁敏, 岳庆炀, 庄华伟, 赵佳. 基于石墨烯纳米带的齿形表面等离激元滤波器的研究. , 2015, 64(10): 108402. doi: 10.7498/aps.64.108402
[18]	邓新华, 袁吉仁, 刘江涛, 王同标. 基于石墨烯的可调谐太赫兹光子晶体结构. , 2015, 64(7): 074101. doi: 10.7498/aps.64.074101
[19]	谢凌云, 肖文波, 黄国庆, 胡爱荣, 刘江涛. 光子晶体增强石墨烯THz吸收. , 2014, 63(5): 057803. doi: 10.7498/aps.63.057803
[20]	徐跃杭, 国云川, 吴韵秋, 徐锐敏, 延波. 基于石墨烯谐振沟道晶体管的高频纳米机电系统信号读取研究. , 2012, 61(1): 010701. doi: 10.7498/aps.61.010701

计量

文章访问数: 10960
PDF下载量: 149
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板