-
设计了一种涂覆石墨烯的非对称椭圆电介质纳米并行线波导. 在椭圆柱坐标系中, 借助于Mathieu函数和坐标变换, 采用多极方法对波导所支持的6个最低阶模式进行了研究, 并分析了这些模式的特性与工作波长、石墨烯费米能以及波导结构参数之间的依赖关系. 结果表明, 调节波导的工作波长、石墨烯的费米能及纳米线之间的间距, 可大幅度调节这些模式的特性. 调节纳米线的半长轴及半短轴, 可以微调这些模式的特性. 在两种条件下, 通过比较涂覆石墨烯的单根椭圆电介质纳米线、对称椭圆电介质纳米并行线与非对称椭圆电介质纳米并行线所支持的基模的性能, 发现本文所设计的波导的性能优于其他两种波导. 本文的研究工作可以为涂覆石墨烯的非对称椭圆电介质纳米并行线波导的设计、制作及应用提供理论基础.An asymmetric graphene-coated elliptical dielectric nano-parallel wires’ waveguide is proposed. By using the multipole method, in the two elliptic cylindrical coordinate systems, firstly, the longitudinal component of the electric field and the magnetic field are expressed by Mathieu functions, then the corresponding angular and radial components are obtained by Maxwell’s equations. The graphene is regarded as a zero-thickness interface with surface conductivity, and the boundary conditions are applied to these interfaces by the point-matching method. A linear algebraic equation system is obtained finally. The effective refractive indices and the field distributions of modes can be obtained by numerically solving the equation. The six lowest order modes supported by the proposed structure are classified, and the dependence of the characteristics of these modes, separately, on the working wavelength, the graphene Fermi energy and waveguide structure parameters are studied. The real part of the effective refractive index, the propagating length, and the quality factor are used to judge the performance of the waveguide. The results reveal that the characteristics of these modes can be greatly changed by altering the working wavelength of the waveguide, the Fermi energy of graphene, and the spacing between nanowires. When the length of the semi-major and the semi-minor axes of the nanowires are modified, the real part of the effective refractive index, the propagating length, and the quality factor can only be changed finely. At the same time, the results obtained by the multipole method are completely consistent with the results from the finite element method. By comparing the performances among the fundamental mode supported by the single graphene-coated elliptical dielectric nanowire, the symmetric graphene-coated elliptical dielectric nano-parallel wires, and the asymmetric graphene-coated elliptical dielectric nano-parallel wires by the means of the FEM based on commercial software (COMSOL), we find that the performances of the proposed waveguide in this paper are superior to those of the other two waveguides. This work can provide a theoretical basis for the design, fabrication, and application of asymmetric graphene-coated elliptical dielectric nano-parallel wires’ waveguide. The proposed structure is expected to be used in the mode conversion and coupling in the future devices.
-
Keywords:
- graphene /
- nanowires /
- waveguides /
- multipole method
[1] Jablan M, Buljan H, Soljacic M 2009 Phys.Rev. B 80 245435
Google Scholar
[2] Vakil A, Engheta N 2011 Science 332 1291
Google Scholar
[3] Parvaei B, Saghai H R, Eldlio M 2018 Opt. Quantum Electron. 50 303
Google Scholar
[4] Balci O, Polat E O, Kakenov N, Kocabas C 2015 Nat. Commun. 6 6628
Google Scholar
[5] Cao M S, Wang X X, Zhang M, Cao W Q, Fang X Y, Yuan J 2020 Adv. Mater. 32 1907156
Google Scholar
[6] Cao M S, Wang X X, Cao W Q, Fang X Y, Wen B, Yuan J 2018 Small 14 1800987
Google Scholar
[7] Wen B, Cao M S, Lu M M, Cao W Q, Shi H L, Liu J, Wang X X, Jin H B, Fang X Y, Wang W Z, Yuan J 2014 Adv. Mater. 26 3484
Google Scholar
[8] He X Q, Ning T G, Pei L, Zheng J J, Li J, Wen X D 2019 Opt. Express 27 5961
Google Scholar
[9] Jia Y H, Gong P, Li S L, Ma W D, Fang X Y, Yang Y Y, Cao M S 2020 Phys. Lett. A 384 126106
Google Scholar
[10] Fang X Y, Yu X X, Zheng H M, Jin H B, Wang L, Cao M S 2015 Phys. Lett. A 379 2245
Google Scholar
[11] Barnes W L, Dereux A, Ebbesen T W 2003 Nature 424 824
Google Scholar
[12] Dionne J A, Sweatlock L A, Atwater H A, Polman A 2005 Phys. Rev. B 72 075405
Google Scholar
[13] Moreno E, Garcia-Vidal F J, Rodrigo S G, Martin-Moreno L, Bozhevolnyi S I 2006 Opt. Lett. 31 3447
Google Scholar
[14] Chang D E, Sørensen A S, Hemmer P R, Lukin M D 2007 Phy. Rev. B 76 035420
Google Scholar
[15] Dionne J A, Sweatlock L A, Atwater H A, Polman A 2006 Phy. Rev. B 73 035407
Google Scholar
[16] Liu P H, Zhang X Z, Ma Z H, Cai W, Wang L, Xu J J 2013 Opt. Express 21 32432
Google Scholar
[17] 彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 光学学报 38 0223002
Google Scholar
Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Opt. Sin. 38 0223002
Google Scholar
[18] Christensen J, Manjavacas A, Thongrattanasiri S, Koppens F H L, Abajo F J G D 2012 ACS Nano 6 431
Google Scholar
[19] Bao Q L, Loh K P 2012 ACS Nano 6 3677
Google Scholar
[20] Gao Y X, Ren G B, Zhu B F, Wang J, Jian S S 2014 Opt. Lett. 39 5909
Google Scholar
[21] Gao Y X, Ren G B, Zhu B F, Liu H Q, Lian Y D, Jian S S 2014 Opt. Express 22 24322
Google Scholar
[22] Liu J P, Zhai X, Wang L L, Li H J, Xie F, Lin Q 2016 Plasmonics 11 703
Google Scholar
[23] Yang J F, Yang J J, Deng W, Mao F C, Huang M 2015 Opt. Express 23 32289
Google Scholar
[24] Liu J P, Zhai X, Xie F, Wang L L, Xia S X, Li H J, Luo X, Shang X J 2017 J. Lightwave Technol. 35 1971
Google Scholar
[25] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 967
Google Scholar
[26] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 1643
Google Scholar
[27] Huang Y X, Zhang L, Yin H, Zhang M, Su H, Li L I, Liang H W 2017 Opt. Lett. 42 2078
Google Scholar
[28] Zhu B F, Ren G B, Yang Y, Gao Y X, Wu B L, Lian Y D, Wang J, Jian S S 2015 Plasmonics 10 839
Google Scholar
[29] 卫壮志, 薛文瑞, 彭艳玲, 程鑫, 李昌勇 2018 67 108101
Google Scholar
Wei Z Z, Xue W R, Peng Y L, Cheng X, Li C Y 2018 Acta Phys. Sin. 67 108101
Google Scholar
[30] Xing R, Jian S S 2016 IEEE Photonics Technol. Lett. 28 2779
Google Scholar
[31] 程鑫, 薛文瑞, 卫壮志, 董慧莹, 李昌勇 2019 68 058101
Google Scholar
Cheng X, Xue W R, Wei Z Z, Dong H Y, Li C Y 2019 Acta Phys. Sin. 68 058101
Google Scholar
[32] Cheng X, Xue W R, Wei Z Z, Dong H Y, Li C Y 2019 Opt. Commun. 452 467
Google Scholar
[33] Wijngaard W 1973 J. Opt. Soc. Am. 63 944
Google Scholar
[34] White T P, Kuhlmey B T, McPhedran R C, Maystre D, Renversez G, Sterke C M, Botten L C 2002 J. Opt. Soc. Am. B 19 2322
Google Scholar
[35] 孙兵, 陈明阳, 周骏, 余学权, 张永康, 于荣金 2010 光学学报 30 59
Google Scholar
Sun B, Chen M Y, Zhou J, Yu X Q, Zhang Y K, Yu R J 2010 Acta Opt. Sin. 30 59
Google Scholar
[36] 孙兵 2013 博士学位论文 (镇江: 江苏大学)
Sun B 2013 Ph. D. Dissertation (Zhenjiang: Jiangsu University) (in Chinese)
[37] Nikitin A Y, Guinea F, Garcia-Vidal F J, Martin-Moreno L 2011 Phy. Rev. B 84 195446
Google Scholar
[38] Erricolo D, Carluccio G 2013 ACM Trans. Math. Soft. 40 8
[39] Lee W M 2011 J. Sound Vib. 330 4915
Google Scholar
[40] Lee W M 2014 Int. J. Mech. Sci. 78 203
Google Scholar
[41] Teng D, Wang K, Li Z, Zhao Y Z 2019 Opt. Express 27 12458
Google Scholar
[42] He X Q, Ning T G, Lu S H, Zheng J J, Li J, Li R J, Pei L 2018 Opt. Express 26 10109
Google Scholar
[43] Ye S, Wang Z X, Sun C R, Dong C B, Wei B Z, Wu B L, Jian S S 2018 Opt. Express 26 23854
Google Scholar
[44] Xue Y, Ye F, Mihalache D, Panoiu N, Chen X 2014 Laser Photonics Rev. 8 L52
[45] Ye F, Mihalache D, Hu B, Panoiu N 2011 Opt. Lett. 36 1179
Google Scholar
[46] Ye F, Mihalache D, Hu B, Panoiu N C 2010 Phys. Rev. Lett. 104 106802
Google Scholar
-
图 1 涂覆石墨烯的非对称椭圆电介质纳米并行线波导的横截面示意图
Fig. 1. The cross section of the double elliptical nano-parallel wires waveguide coated with graphene.
图 2 在
${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,$\lambda = 7\;\text{μm}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 40\;{\rm{nm}}$ 条件下, 6个最低阶模式的模式合成图 (a)−(f)、电场的z分量分布图(g)−(l)和电场强度分布图(m)−(r)Fig. 2.
${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,$\lambda = 7\;\text{μm}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ and$d = 40\;{\rm{nm}}$ , pattern composition diagram (a)−(f), the z-component of electric field${E_z}$ (g)−(l) and the electric field distribution$\left| E \right|$ for the six lowest order modes (m)−(r).
图 3 当
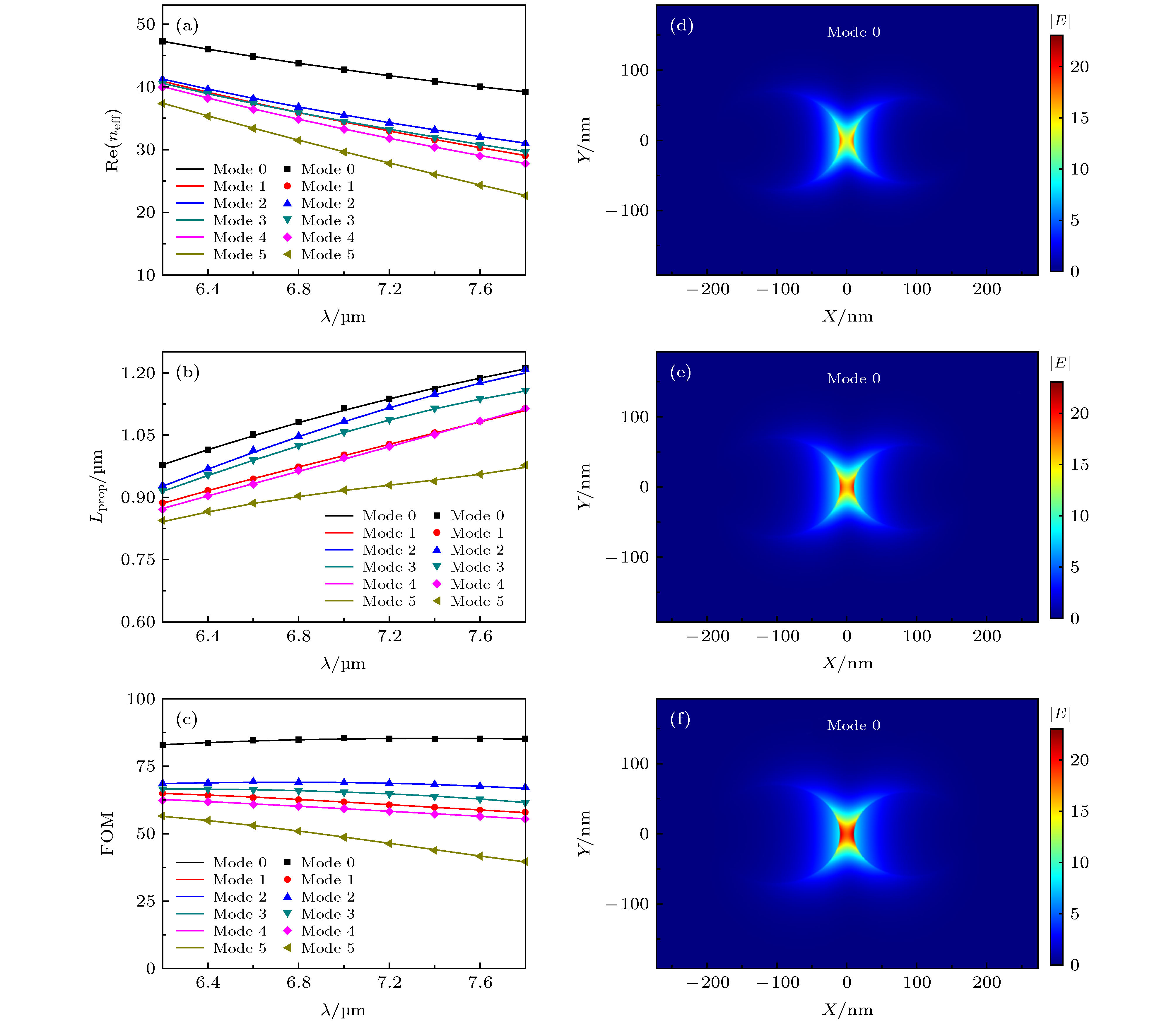
${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 20\;{\rm{nm}}$ 时, (a)有效折射率${\rm{Re}} ({n_{{\rm{eff}}}})$ 、(b)传播长度$L_{\rm{prop}}$ 、(c)品质因数FOM随工作波长$\lambda $ 变化关系图; (d)$\lambda = 6.2\; \text{μm}$ , (e)$\lambda = 7\;\text{μm}$ , (f)$\lambda = 7.8\; \text{μm}$ 时基模的电场强度变化图Fig. 3. The dependence of (a) the effective refractive index
${\rm{Re}} ({n_{{\rm{eff}}}})$ , (b) the propagation length$L_{\rm{prop}}$ , (c) the quality factor FOM for the six lowest order modes on the wavelength$\lambda $ at${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 20\;{\rm{nm}}$ . And the electric field distribution$\left| E \right|$ for (d)$\lambda = 6.2\; \text{μm}$ , (e)$\lambda = 7\;\text{μm}$ , (f)$\lambda = 7.8\; \text{μm}$ .
图 4 当
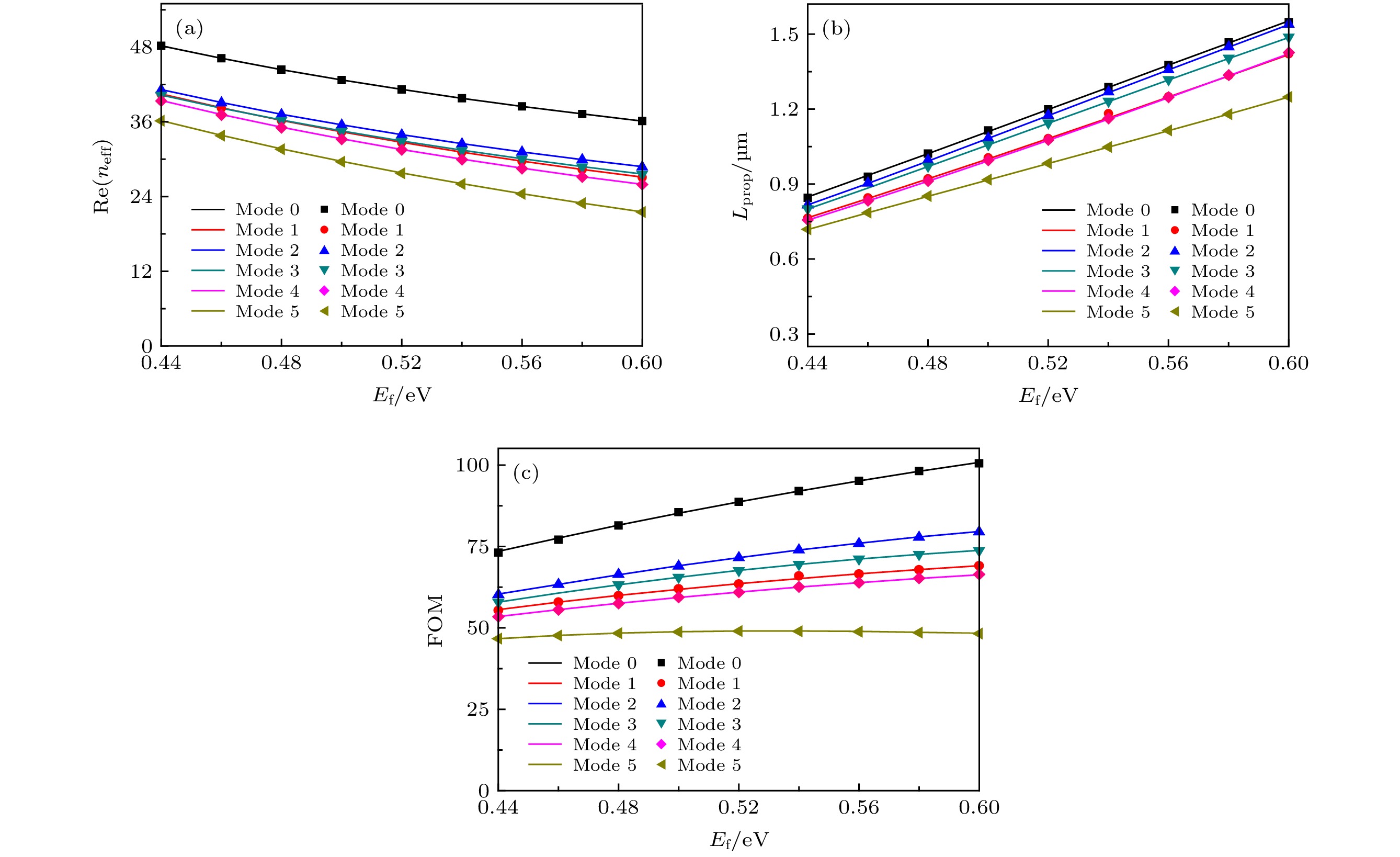
$\lambda = 7\;{\text{μ}\rm{m}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 20\;{\rm{nm}}$ 时 (a)有效折射率${\rm{Re}} ({n_{{\rm{eff}}}})$ 、(b)传播长度${L_{{\rm{prop}}}}$ 和(c)品质因数FOM随石墨烯费米能${E_{\rm{f}}}$ 变化关系图Fig. 4. The dependence of (a) the effective refractive index
${\rm{Re}} ({n_{_{{\rm{eff}}}}})$ , (b) the propagation length${L_{{\rm{prop}}}}$ and (c) the quality factor FOM for the six lowest order modes on the graphene Fermi levels${E_{\rm{f}}}$ at$\lambda = 7\;{\text{μ}\rm{m}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 20\;{\rm{nm}}$ .
图 5 当
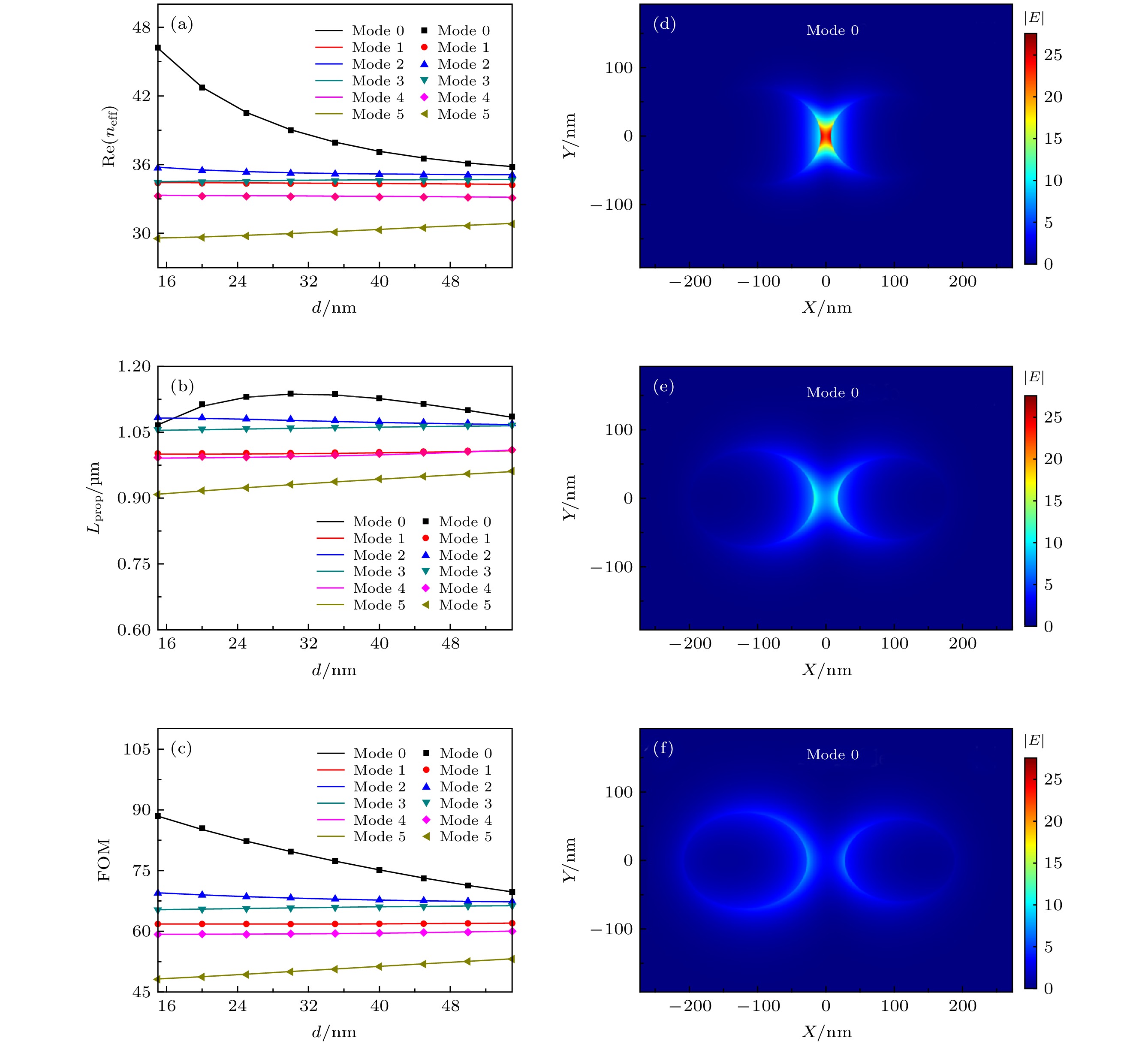
$\lambda = 7\;\text{μm}$ ,${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ (a)有效折射率${\rm{Re}} ({n_{{\rm{eff}}}})$ , (b)传播长度${L_{{\rm{prop}}}}$ , (c)品质因数FOM随两纳米线间距d变化关系图; (d)$d = 15\;{\rm{nm}}$ , (e)$d = 35 \;{\rm{nm}}$ , (f)$d = 55 \;{\rm{nm}}$ 时基模的电场强度变化图Fig. 5. The dependence of (a) the effective refractive index
${\rm{Re}} ({n_{{\rm{eff}}}})$ , (b) the propagation length${L_{{\rm{prop}}}}$ , (c) the quality factor FOM for the six lowest order modes on the distance d between two nanowires at$\lambda = 7\;\text{μm}$ ,${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ; the electric field distribution$\left| E \right|$ for (d)$d = 15\;{\rm{nm}}$ , (e)$d = 35 \;{\rm{nm}}$ , (f)$d = 55 \;{\rm{nm}}$ .
图 6 当
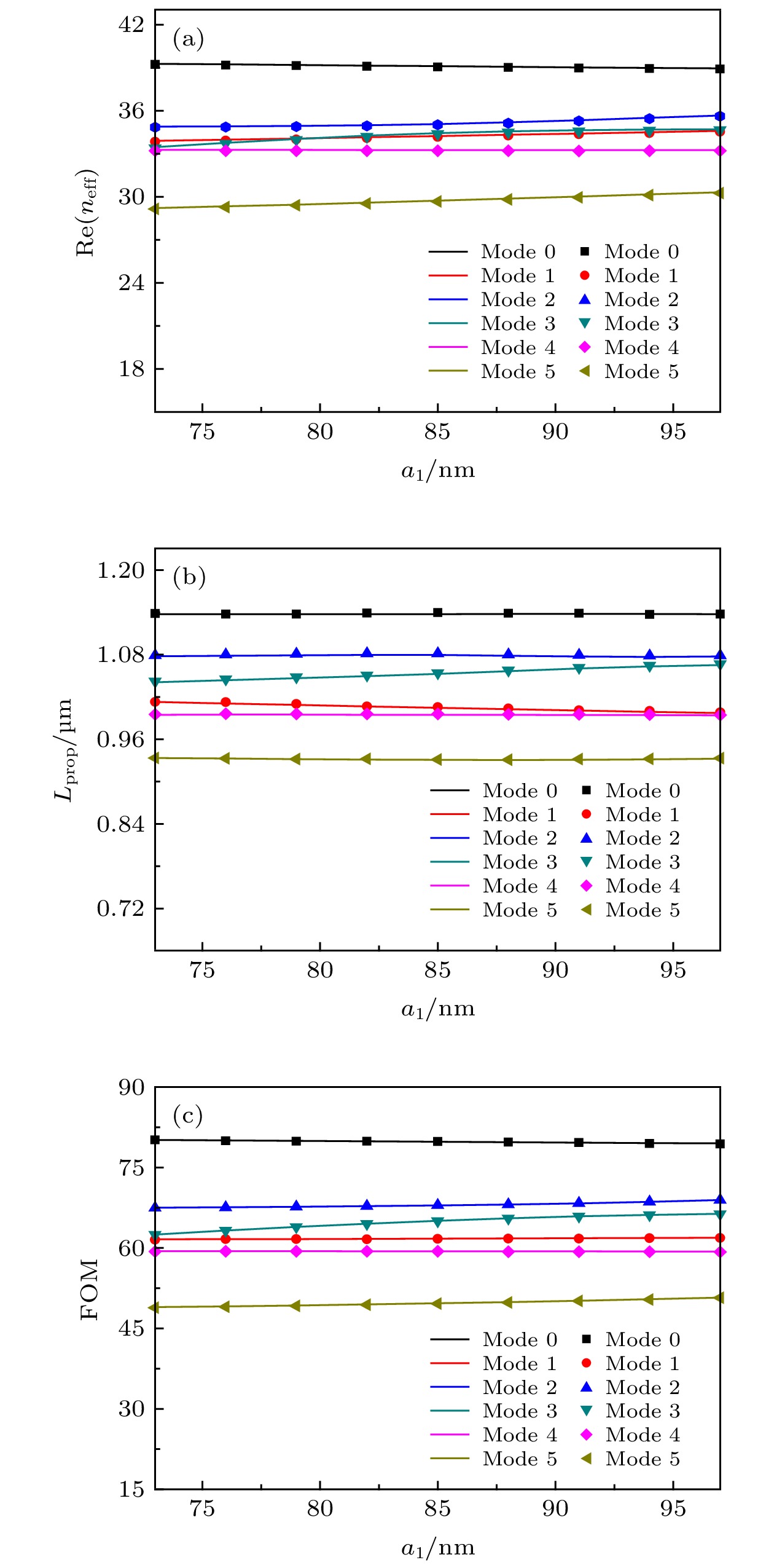
$\lambda = 7\;\text{μm}$ ,${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 30\;{\rm{nm}}$ 时, (a)有效折射率实部${\rm{Re}} ({n_{{\rm{eff}}}})$ 、(b)传播长度${L_{{\rm{prop}}}}$ 和(c)品质因数FOM随1号纳米线半长轴${a_1}$ 变化关系图Fig. 6. When
$\lambda = 7\;\text{μm}$ ,${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${b_1} = 70\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 30\;{\rm{nm}}$ , the dependence of (a) the effective refractive index${\rm{Re}} ({n_{{\rm{eff}}}})$ , (b) the propagation length${L_{{\rm{prop}}}}$ , and (c) the quality factor FOM for the six lowest order modes on the length of${a_1}$ on the No.1 nanowire.
图 7 当
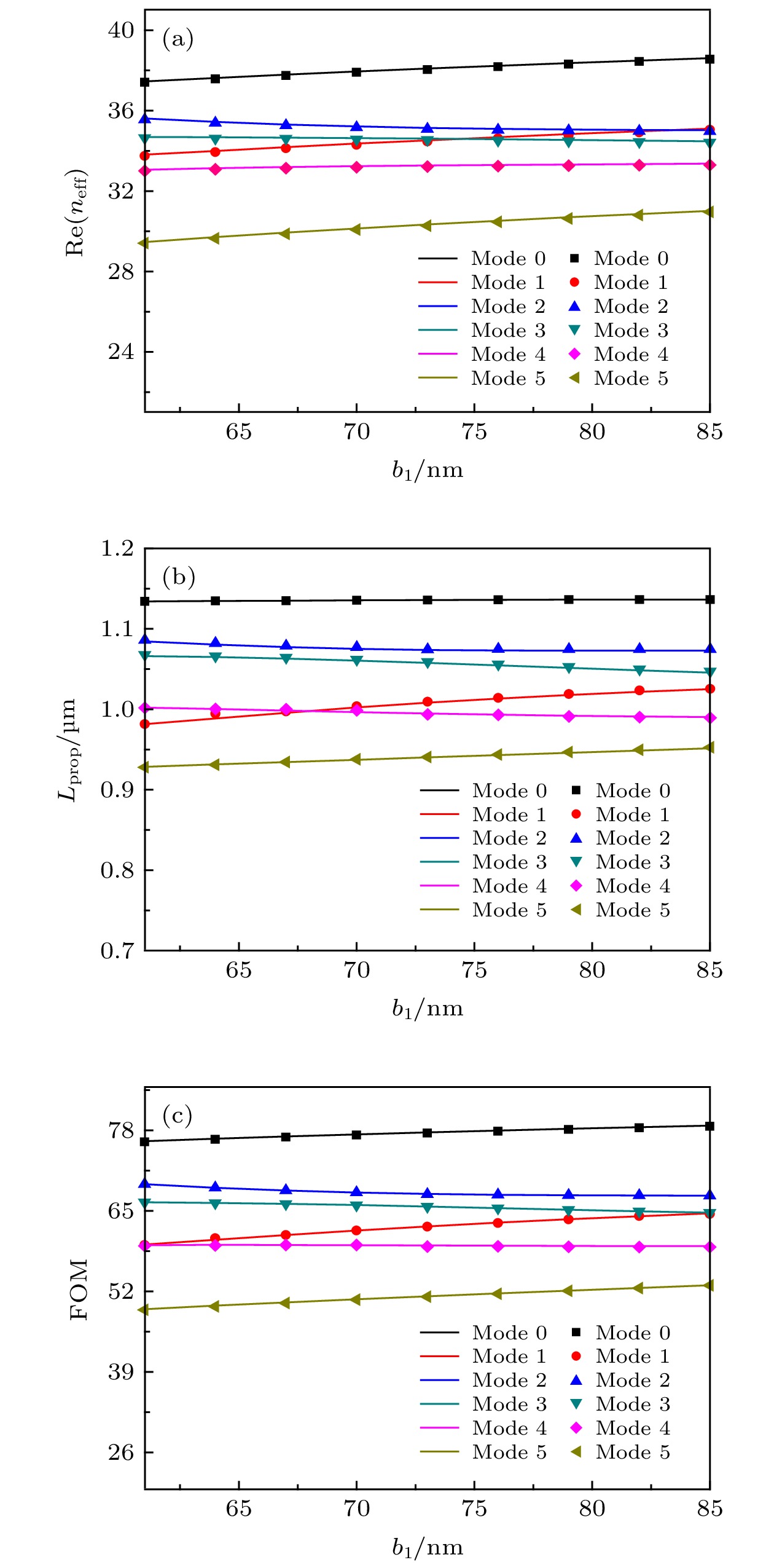
$\lambda = 7\;\text{μm}$ ,${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 35\;{\rm{nm}}$ 时, (a)有效折射率实部${\rm{Re}} ({n_{{\rm{eff}}}})$ 、(b)传播长度${L_{{\rm{prop}}}}$ 和(c)品质因数FOM随1号纳米线半短轴b1变化关系图Fig. 7. When
$\lambda = 7\;\text{μm}$ ,${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ ,${a_1} = 90\;{\rm{nm}}$ ,${a_2} = 80\;{\rm{nm}}$ ,${b_2} = 60\;{\rm{nm}}$ ,$d = 35\;{\rm{nm}}$ , the dependence of (a) the effective refractive index${\rm{Re}} ({n_{{\rm{eff}}}})$ , (b) the propagation length${L_{{\rm{prop}}}}$ and (c) the quality factor FOM for the six lowest order modes on the length of${b_1}$ on the No.1 nanowire.
图 8 当
${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ 时, 三种波导结构所支持的基模的 (a)有效折射率${\rm{Re}} ({n_{{\rm{eff}}}})$ 、(b)传播长度和${L_{{\rm{prop}}}}$ 和(c)品质因数FOM随波长$\lambda $ 变化的关系图Fig. 8. When
${E_{\rm{f}}} = 0.5\;{\rm{eV}}$ , the dependence of (a) the effective refractive index${\rm{Re}} ({n_{{\rm{eff}}}})$ , (b) the propagation length${L_{{\rm{prop}}}}$ and (c) the quality factor FOM of the fundamental mode supported by the three structures on the wavelength$\lambda $ .
图 9 当
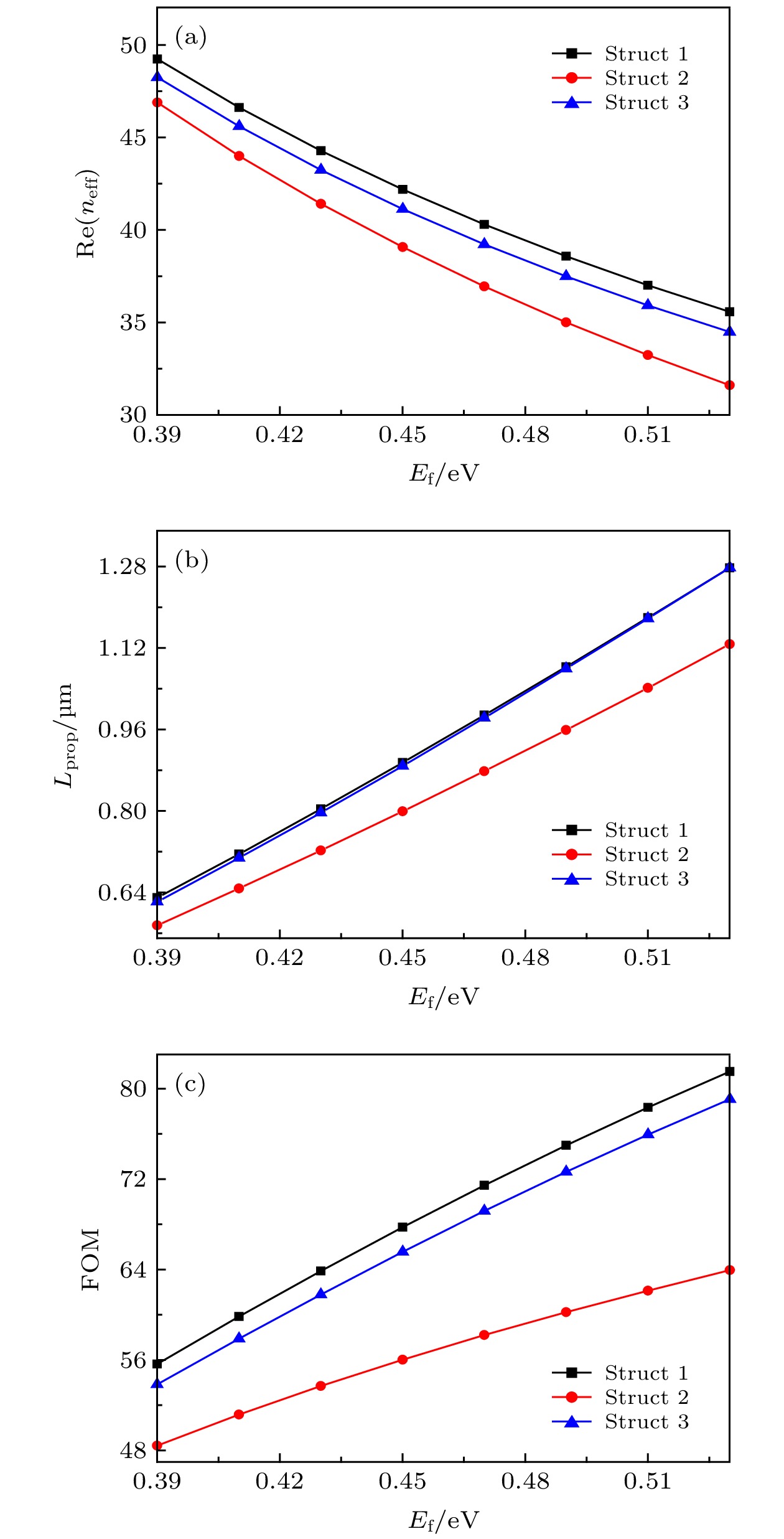
$\lambda = 7\;{\rm{\mu m}}$ 时, 三种波导结构所支持的基模的 (a)有效折射率${\rm{Re}} ({n_{{\rm{eff}}}})$ 、(b)传播长度${L_{{\rm{prop}}}}$ 和(c)品质因数FOM随石墨烯的费米能级变化的关系图Fig. 9. When
$\lambda = 7\;{\rm{\mu m}}$ , the dependence of (a) the effective refractive index${\rm{Re}} ({n_{{\rm{eff}}}})$ , (b) the propagation length${L_{{\rm{prop}}}}$ and (c) the quality factor FOM of the fundamental mode supported by the three structures on the Fermi levels. -
[1] Jablan M, Buljan H, Soljacic M 2009 Phys.Rev. B 80 245435
Google Scholar
[2] Vakil A, Engheta N 2011 Science 332 1291
Google Scholar
[3] Parvaei B, Saghai H R, Eldlio M 2018 Opt. Quantum Electron. 50 303
Google Scholar
[4] Balci O, Polat E O, Kakenov N, Kocabas C 2015 Nat. Commun. 6 6628
Google Scholar
[5] Cao M S, Wang X X, Zhang M, Cao W Q, Fang X Y, Yuan J 2020 Adv. Mater. 32 1907156
Google Scholar
[6] Cao M S, Wang X X, Cao W Q, Fang X Y, Wen B, Yuan J 2018 Small 14 1800987
Google Scholar
[7] Wen B, Cao M S, Lu M M, Cao W Q, Shi H L, Liu J, Wang X X, Jin H B, Fang X Y, Wang W Z, Yuan J 2014 Adv. Mater. 26 3484
Google Scholar
[8] He X Q, Ning T G, Pei L, Zheng J J, Li J, Wen X D 2019 Opt. Express 27 5961
Google Scholar
[9] Jia Y H, Gong P, Li S L, Ma W D, Fang X Y, Yang Y Y, Cao M S 2020 Phys. Lett. A 384 126106
Google Scholar
[10] Fang X Y, Yu X X, Zheng H M, Jin H B, Wang L, Cao M S 2015 Phys. Lett. A 379 2245
Google Scholar
[11] Barnes W L, Dereux A, Ebbesen T W 2003 Nature 424 824
Google Scholar
[12] Dionne J A, Sweatlock L A, Atwater H A, Polman A 2005 Phys. Rev. B 72 075405
Google Scholar
[13] Moreno E, Garcia-Vidal F J, Rodrigo S G, Martin-Moreno L, Bozhevolnyi S I 2006 Opt. Lett. 31 3447
Google Scholar
[14] Chang D E, Sørensen A S, Hemmer P R, Lukin M D 2007 Phy. Rev. B 76 035420
Google Scholar
[15] Dionne J A, Sweatlock L A, Atwater H A, Polman A 2006 Phy. Rev. B 73 035407
Google Scholar
[16] Liu P H, Zhang X Z, Ma Z H, Cai W, Wang L, Xu J J 2013 Opt. Express 21 32432
Google Scholar
[17] 彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 光学学报 38 0223002
Google Scholar
Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Opt. Sin. 38 0223002
Google Scholar
[18] Christensen J, Manjavacas A, Thongrattanasiri S, Koppens F H L, Abajo F J G D 2012 ACS Nano 6 431
Google Scholar
[19] Bao Q L, Loh K P 2012 ACS Nano 6 3677
Google Scholar
[20] Gao Y X, Ren G B, Zhu B F, Wang J, Jian S S 2014 Opt. Lett. 39 5909
Google Scholar
[21] Gao Y X, Ren G B, Zhu B F, Liu H Q, Lian Y D, Jian S S 2014 Opt. Express 22 24322
Google Scholar
[22] Liu J P, Zhai X, Wang L L, Li H J, Xie F, Lin Q 2016 Plasmonics 11 703
Google Scholar
[23] Yang J F, Yang J J, Deng W, Mao F C, Huang M 2015 Opt. Express 23 32289
Google Scholar
[24] Liu J P, Zhai X, Xie F, Wang L L, Xia S X, Li H J, Luo X, Shang X J 2017 J. Lightwave Technol. 35 1971
Google Scholar
[25] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 967
Google Scholar
[26] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 1643
Google Scholar
[27] Huang Y X, Zhang L, Yin H, Zhang M, Su H, Li L I, Liang H W 2017 Opt. Lett. 42 2078
Google Scholar
[28] Zhu B F, Ren G B, Yang Y, Gao Y X, Wu B L, Lian Y D, Wang J, Jian S S 2015 Plasmonics 10 839
Google Scholar
[29] 卫壮志, 薛文瑞, 彭艳玲, 程鑫, 李昌勇 2018 67 108101
Google Scholar
Wei Z Z, Xue W R, Peng Y L, Cheng X, Li C Y 2018 Acta Phys. Sin. 67 108101
Google Scholar
[30] Xing R, Jian S S 2016 IEEE Photonics Technol. Lett. 28 2779
Google Scholar
[31] 程鑫, 薛文瑞, 卫壮志, 董慧莹, 李昌勇 2019 68 058101
Google Scholar
Cheng X, Xue W R, Wei Z Z, Dong H Y, Li C Y 2019 Acta Phys. Sin. 68 058101
Google Scholar
[32] Cheng X, Xue W R, Wei Z Z, Dong H Y, Li C Y 2019 Opt. Commun. 452 467
Google Scholar
[33] Wijngaard W 1973 J. Opt. Soc. Am. 63 944
Google Scholar
[34] White T P, Kuhlmey B T, McPhedran R C, Maystre D, Renversez G, Sterke C M, Botten L C 2002 J. Opt. Soc. Am. B 19 2322
Google Scholar
[35] 孙兵, 陈明阳, 周骏, 余学权, 张永康, 于荣金 2010 光学学报 30 59
Google Scholar
Sun B, Chen M Y, Zhou J, Yu X Q, Zhang Y K, Yu R J 2010 Acta Opt. Sin. 30 59
Google Scholar
[36] 孙兵 2013 博士学位论文 (镇江: 江苏大学)
Sun B 2013 Ph. D. Dissertation (Zhenjiang: Jiangsu University) (in Chinese)
[37] Nikitin A Y, Guinea F, Garcia-Vidal F J, Martin-Moreno L 2011 Phy. Rev. B 84 195446
Google Scholar
[38] Erricolo D, Carluccio G 2013 ACM Trans. Math. Soft. 40 8
[39] Lee W M 2011 J. Sound Vib. 330 4915
Google Scholar
[40] Lee W M 2014 Int. J. Mech. Sci. 78 203
Google Scholar
[41] Teng D, Wang K, Li Z, Zhao Y Z 2019 Opt. Express 27 12458
Google Scholar
[42] He X Q, Ning T G, Lu S H, Zheng J J, Li J, Li R J, Pei L 2018 Opt. Express 26 10109
Google Scholar
[43] Ye S, Wang Z X, Sun C R, Dong C B, Wei B Z, Wu B L, Jian S S 2018 Opt. Express 26 23854
Google Scholar
[44] Xue Y, Ye F, Mihalache D, Panoiu N, Chen X 2014 Laser Photonics Rev. 8 L52
[45] Ye F, Mihalache D, Hu B, Panoiu N 2011 Opt. Lett. 36 1179
Google Scholar
[46] Ye F, Mihalache D, Hu B, Panoiu N C 2010 Phys. Rev. Lett. 104 106802
Google Scholar
下载:
计量
- 文章访问数: 6110
- PDF下载量: 139
- 被引次数: 0
